Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

270 Гпава 7

Следует

заметить,

что

функция у-

\х\

не имеет

производной

точке

Хо,

так как

/Л^)"^

^^^

~.—

='""^'

a//(0)=

li^^ т^ =

б) Представим функцию

виде

У^

2х-3,

х>—;

-2л:

jc<—,

тогда

У =

3^ =

^>-;

-2,

х<|.

в) Представим функцию

виде

\е^\

х>0;

[е"^%

x<0.

В этом случае

производная будет

\le^\ х>0;

[-2е"'%

х<0.

г) Представим функцию

виде

\2х, х>\\

тогда

У =

-l<x<l;

-2х,

X <

-1,

л:>1;

О,

-1<х<1;

-2,

х<-1.

аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ фУНКиИИ

271

13.

Найти производные у_ {х^), у^ {х^) для функций:

f X,

< 1;

а) У = \ 2^0 ^1

''«"^'

Решение, а) Находим производную

,^|1,

х<1;

[-2х +

х>1.

и вычислим пределы производной слева

справа в точке х^=\:

у'_{1)=Ш\

\, X(l)=Um(-2x+2) = 0.

б) Находим производную

jc->l+0

е" VI-е"

и вычислим пределы производной слева и справа в точке

дг^

О:

/(0)=lim-

-1,

л(0)=Ит.

= 1.

Касательные к кривой в точке

JCQ

показаны на рис. 7.3.

Рис. 7.3

272

Гпава

) представим заданную

У^\

-2х,

2х,

чем

производную

[-2,

|о,

функцию в виде

хе]-оо,-2];

хе]-2,2];

Хб]2,оо[

хе]-оо,-2];

хе]-2,2];

Хб]2,оо[.

3 ^ г г

1.4. Найти производные:

а)

У = '-1

j-+4Vx

б) >' =

A:^COSJC;

В) у =

у-

г)

f{x)

jt^

вычислить

х'+\

' - ^ ' 3

/'(О),/0)'/(-!)•

Решение,

а)

Преобразуем функцию

виду, удобному

для

дифференцирования. Пользуясь основными правилами диффе-

ренцирования

таблицей производных, имеем

2 х' ^

б) Здесь имеет место случай произведения двух функций,

поэтому

(х^) cosx + x^(cosx) =3x^cosx-Jc^sinx

в) Поскольку имеет место частное двух функций,

то

^Jx'^j(x'+l)-(x')(x'+l'j ^2х'+2х-2х'

^ 2х

^ (x'+\f (x'+lf

(х'

+ \)

аИФФЕРЕНиИАПЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ 273

г) Находим производную f'{x)

x^ —2х и вычисляем ее

значения в точках

О,

х =

-1,

т. е. находим частные зна-

чения производной в этих точках:

/•(0) =

0,/'(1)

= -1,/'(-1) = 3.

x^-4x+4

1.5. Найти производные: а) у

\п-

х^+Ах+Л'

+ \

б)

= In , ; ъ) у

logj Vtg" 2х; v) у

In^

cos J

Vx^-jc +

Решение, a) Упростим логарифмируемое выражение

y =

\r\

(х-2^ _. х-2

yX + lj

= 21n-

х+2

х — 2

Полагая у = 2\пи,

тд,е

и = , применяем правило диф-

х+2

ференцирования сложной функции

+ 2{х-2)'{х + 2)-{х-2){х + 2)' _ 8

/ = 2(1п«Х •"х=2

х-2

(x+2f х'-4

б)Полагая у

\пи, где и= . , имеем

yJx^-x+1

г- л/х^-лс +

1-(х+1)

/ /, ч' / Vx -x + l 2Vx^-x

l _

V =(1ПМ) Ы, = ; ^^ =

1-Х 3 1-х

2(x+l)(x'-x + l) 2(х + 1)'"

в) Упростим логарифмируемое выражение

log2

функцию

- 2

д'

= logj tg^ 2х

=—log2

tg2x. Дифференцируем как сложную

274

Гпава 7

1 1

-2 =

3 tg2jcln2cos^2jc 3sin4xln2

г) Дифференцируем как сложную функцию

y = 31n^cos

(

3 ^х

cos—V

-sin-

- = -tg —In COS—.

1.6. Найти производные: а) z =

jce"

+ ае ";

\\-Y

6)>' = e-''(sin3x+cos3x); в) z = lnJ--—; г)

e^'"'^

+ 54

Решение,

Дифференцируем как сумму сложных функций

— £ 1

( \\

..--е-.

б) Дифференцируем как произведение сложных функций

/ =

e'^""

(-3) (sin

3JC

+ cos

3JC)

e'^""

(cos Зх

• 3

+ (- sin

3x) З)

-ee"^""

sin

3JC.

1 1-2'^

в) Упростим функцию у = — In J. Находим производ-

ную как от сложной функции

, 1

+ г

2Чп2(1

+ 2^)+(1-2^)2'1п2 2Чп2

У =Х"

2 1-2^

2^)^

2^'-1

г) Дифференцируем как сумму сложных функций

1 -i

/ = e""'^-3sin'xcosx+5^4n5--x ' =

Зе''"'*

sin'

Xcosд:

5^"'x'^

In5.

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ

275

1-Х

1.7. Найти производные: а)

arctgj-

;

б) w=arcsinVl-4r; в) r = arccos "" ^; г) y

= Ъшztge

Решение,

а)

Находим производную

как

от сложной функции

у =•

I lfl-x\2-{l +

x)-{\-x)_

1-д: 2

1+л:

(1 +

2л/Г^

1 +

д:

б)

Производная равна

1 1 (-4) _

и =

^1-(1-4г) 2 VT^ 7^(1-4г)'

в)

Производная равна

1 f 1\^ I 3

4) \4

4(р-3<р'

г =

—

r2-3<pY

г)

Производная равна

-0)

2х

1 +

е'з

_2х

1 +

1 2 -^ 1-2 "^

1.8. Найти производные: а)

= sn т^+сп --;

б)

= thx

cthx.

Решение, а) Дифференцируем как сумму

2sh—ch

H-2ch—sh

= shx.

2 2 2 2 2 2

6) Дифференцируя как сумму и пользуясь свойствами ги-

перболических

функций,

имеем

,_ 1 1 _sh^x-ch"jc_ 4

ch^x sh^jc sh^xch^jc sh^2:^

276

Гпава 7

1.9. Найти производные:

а) у =

х^,

х<0;

ln(l +

x^),

л:>0,

б) у=^<

хе ",

|jc|<0;

|jc|

> 0,

в)

Г2-;с,

-l<jc<2;

jc^

5JC

2 <

< 3;

jc~3,

3<jc<4,

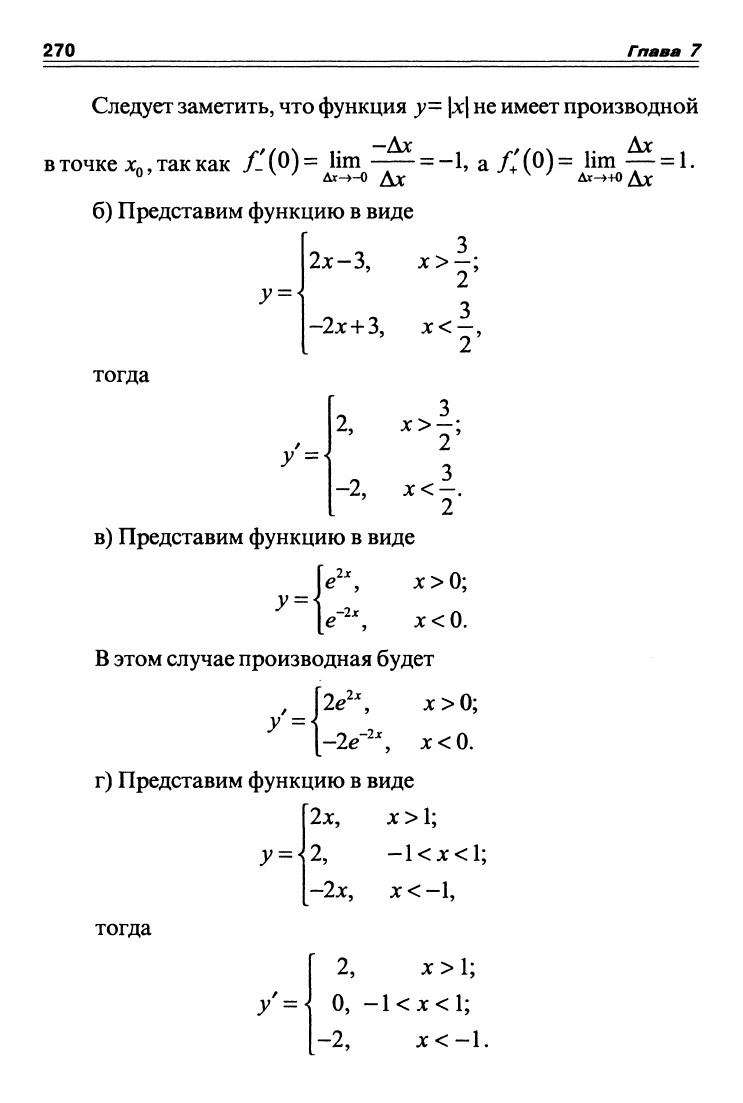
построить график функции и производной.

Решение, а) Поскольку функция на разных участках имеет

различный вид, то для этих участков

[2JC,

< 0;

У =\ 2х

1 +

2 '

jc>0.

б) Находим производную на разных участках

[е"^(1-х),

|jc|<0;

[о,

|jc|

> 0.

в) Находим производную на разных участках

Г-1,

-l<jc<2;

у = <2х-5, 2<д:<3;

[1,

< 4.

Строим график функции и график производной

(рис.

7.4).

Рис, 7.4

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ

277

1.10. Найти Производные: а)

= |sinjc|; б)

= |arctgx|.

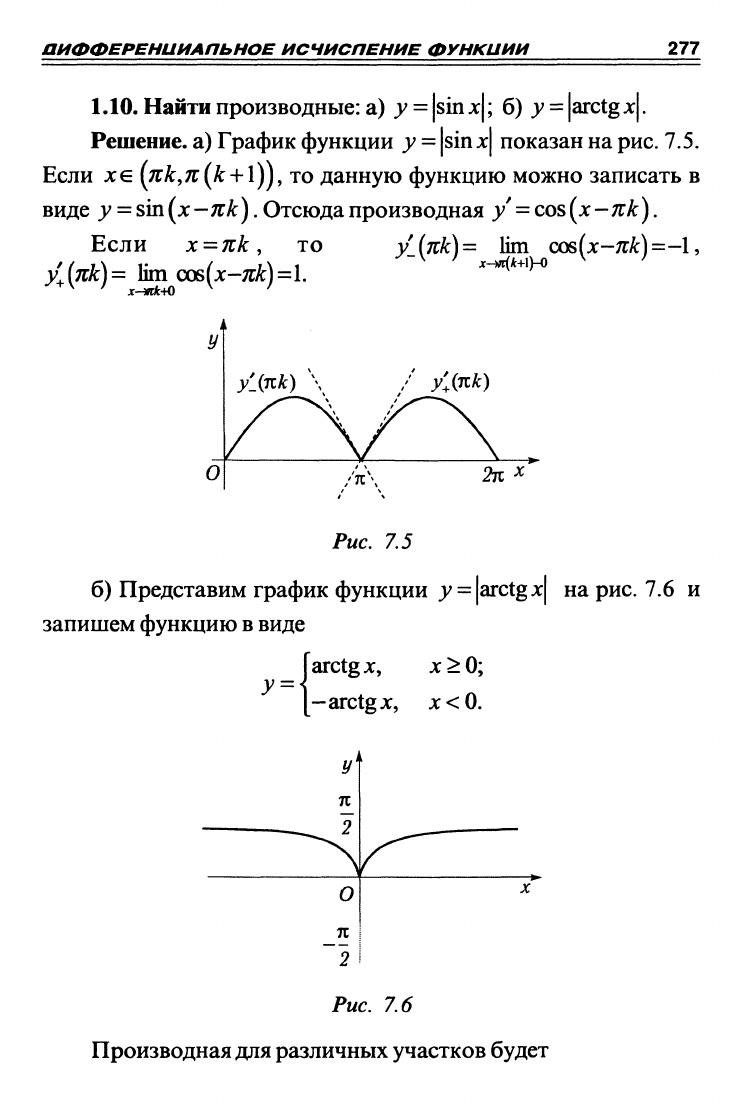
Решение, а) График функции у = |sinjc| показан на

рис.

7.5.

Если л:е

(жк,п{к +

\)),

ТО

данную функцию можно записать в

виде y

sm{^x-Kk). Отсюда производная у = cos(х-я/г).

Если х = кк, то y_{7tk)= lim cos{x'-7ik)=-l,

у^[кк)=

\im cos{x-7tk)=l.

x-^k+\)-0

х-жк-^О

/ /Лпк)

Рис. 7.5

б) Представим график функции

д'

|агс1§л:|

на рис. 7.6 и

запишем функцию в виде

[arctgx, л;>0;

—arctgAT, jc<0.

Рис. 7.6

Производная для различных участков будет

278 Гпава

Г'

^^0'

jc<0.

х^'

производная слева

>^'(0)=lim

j^ =-1;

справа

1.11. Найти производные функций, обратных

заданным:

а)

jc;

б)

х;

в) у =

х;

г) ;; =

cth х.

Решение, а) По правилу дифференцирования обратной фун-

кции получим

(Arsh;;)

=-7 = = . =^= .

:^^

chx

+ sh'jc

V/+1

отсюда, переходя

обычным обозначениям, имеем

(Arshx/=-p==.

Vl +

б)

По

правилам дифференцирования обратной функции

имеем

(Archj;/=

—

= —-=:

откуда (Archjc)

= . (И^О*

в) производная обратной функции равна

(Arthj^/=-V =

ch'^

—L_

_L-,

-^^ J: 1-tg^x 1-/

откуда (Arthx)

=- 2", (кНО'

аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ

ФУНКЦИИ

279

г)

производная обратной функции равна

(Arcthj;) =-7

-sh^jc

= "-

откуда (Arcthx) =—^—, (|A:|>1).

1.12. Пользуясь результатами предьщущего

примера,

найти

2х

производные: а)

Arch In х; б)

У =

Arctn —^—--.

Решение,

а) По

правилу дифференцирования сложных фун-

кций имеем

.^1 1_ 1

б)

Функция

сложная,

поэтому

1 2(X'+1)-2X-2JC

2(JC'+1)

(й1-

7.2. Производные функций,

не являющихся явно заданными

1°.

Пусть функция

задана уравнением/(х,у) =

О,

не

разре-

шенным относительно

у,

то есть у

есть

неявная функция от

х.

Чтобы найти производную от неявной функции

аргумен-

та

дифференцируем по х обе части этого равенства, считая у

функцией X, Из полученного равенства определяем искомую

производную

j^',

которая, как правило, будет зависеть oTxiAy

у=(р{х,уУ

2°.

Если

функциональная зависимость

между

переменными

ИД'

задана параметрически