Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

280 Гпава 7

производная от

по

д:

равна

j;^

= ^, а от х по

>^:

-^д^

- ~7

•

Х^

Уг

3^.

Логарифмическое

диференцирование.

Если

у—и^,

то

/ V-\ f г V 'л

У =vu и +и V ти,

т. е. производная показательно-степенной функции состоит из

двух слагаемых: первое получается, если рассматривать функ-

цию при дифференцировании как степенную, второе как пока-

зательную.

4°.

Если основание логарифма log^ и является некоторой

функцией

л:,

то при нахождении производной целесообразно пе-

рейти к натуральным логарифмам

= log,w=-;—,

= w(x), v

v{x).

2.1.

Найти производные

у'^'-^)

У = cos

(л:

jv);

б)

ё^

+4xy-j^

=1;

и производные х[:в) хЫу-у1пх=^\;

г) х^у^-4\пу = 21пх.

Решение,

а)

Дифференцируем обе части по х, считая

д'

слож-

ной функцией, зависящей от х

/ = -sm(x+у)(1-\- /) =

-sin{x+у)-

/sm(x+у).

Откуда y(l + sin(x + 7)) = -sin(x+j^) или

sin(x

>;)

У =":

l +

sin^x +

б)

Дифференцируя обе части равенства по х, получим

еУ+4(>; +

х/)-2х

= 0.

ПИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ

281

Разрешая равенство относительно

>^',

получим

, 2{х^2у)

У - -

е'+4х

в)

Дифференцируем обе части равенства по

у,

считая х слож-

ной функцией, зависящей от;;

'1 . ^

X my-h —

( 1 Л

Injc

j;—jc'

=0.

Разрешая равенство относительно х', получим

1пх--

\пу-

г) Дифференцируем обе части равенства по у

2хху^

н-

2х^у = 2—х'.

У ^

2 2

X у

f_y

Отсюда ^

—

-.{г-хУ)

2.2.

Найти производные у'^:

cos'^^

а)

б)

\х = е

_cos2/.

|j;

= lnsinr;

и производные

х^:

= arctgv/;

в)

г)

У =

l +

y = ln COS

(р

282

Гпатт

Решение. а) Находим — = —cos^fsin/ и

dt 2

dy 3 . у.

-— =

-sm/2

cos ?. Отсюда

at 2

3 . у,

y>—^ V

->/etg^-

—cos^^/sin/

6) Находим —

-2e'°'^'

sin

~=^

ctg /.

dt dt sin^

Отсюда /= ' -—

в)

Находим

dy _2t{\ + t)-t' _e+2t ^ dx^24t ^ 1

dt~ {\+tf ~(l+0' ^* 1 + ^ 2^t{\ + t)

Отсюда

d!x:^

(1 + 0^

^ 1+f

йГу 2Vf(l+r)f(f + 2) 2f^(r + 2)

• ^

dy 1 ^'" 9 1 fi) Л; 1 1

г)Находим —

= —

=—tg—

и—

d9 2^os^ 2 b d<p 2^^г^

2 2

Отсюда ^y

2cos^^tg^ '^"P

2 ^2

2.3.

Найти

производные:

jy =

л:*

; б) y

{x-lf'4I+2 ^ г

:г

. . ^

в) y

- 3 ; г) y

x e smixmx.

(x-3)

sin2x.

аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ фУНКиИИ

283

Решение, а) Прологарифмируем правую и левую часть

jc^

JC.

Найдем производные от правой и левой части по

считая

сложной функцией, зависящей от х

у г 1

У X

Отсюда / = (21njc-bl)x^'^V

б) Логарифмируя правую и левую часть, имеем

д'

= sin 2x

JC.

Откуда

У ^ ^1 sin2x , sin2x

— = 2cos2xlnjc + , / = х'*"^^

У X

^ ^ ^ , sin2jc

2cos2xlnjc +

в) Логарифмируя правую и левую часть, имеем

1п>;

= 21п(д:-1)+-1п(;с + 2)-31п(д:-3).

о /21

Отсюда ^^ = 1—;

у х-\ 3(х+2) х-Ъ

или

, {x-Xi4xVi

У =

х—\

3(x+2) х—Ъ

{х-Ъ)'

г) Логарифмируем правую и левую часть

ln>^

= 21nx +

jc^

+lnsin3x+lnthx.

Берем производные

У-^иъх^^

у X

Откуда

е""

sinSxthjc

3COS3JC

1 1

sin3x thxch X

f 2

-4-3x^3ctg3jc+

X sh2jc

284 Гпавв 7

2.4.

Найти производные функций: а) >Hcg^^ б) j;=log^sinA;

в)

= log^3x\

Решение, а) Перейдем к натуральному логарифму у =

Injc

тогда / = -—.

jcln X

б) Представим функцию в виде у , тогда

In cos X

cosx- sinx, .

IncosxH-

sin

111 \j\JZi Л. П 111 Olll Л, ,1 . X 1 •

/^ sinx cosx ^ctgxlncosx

tgxlnsmx

In^cosx In^cosx

xlnx X

в) Перейдем к натуральному логарифму

У~~Гу^—~Т?

от-

, 1

сюда V =

—.

7.3. Производные высших порядков

1°.

Пусть функция;^ =/W имеет производную>^', которая

является некоторой функцией от х.

Производной второго порядка называется производная от

d-y

первой производной и обозначается v"или/"

(х),

или —Т

•

ах

Производная от второй производной называется третьей

производной от функции/(х) и обозначается

j;'"или/"'

(х),

или

dx^ *

Аналогично определяются производные четвертого, пятого

и более старших порядков, так

j;^"^

— производная я-го порядка.

d'y

2°.

Вторая производная от неявной функции —у находит-

ах

ся

дифференцированием функции

j;'

= ^

(х,

j;)

по переменной х,

учитывая при этом, что у есть функция от х.

ДИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ 285

3°.

Вторая производная от функции у

по х,

заданной пара-

метрически, равна

=(л);=^=^.

Х^ X

последнем выражении точки означают дифференцирова-

ние

по г.

{у'У

Третья производная у^^ =

"^f^

и т.

д.

4^.

Производную

п-то

порядка от произведения

двух

функ-

ций

удобнее находить

по

формуле Лейбница

^ ^ 1! 2!

гдеС*= ^——биномиальные коэффициенты, « =u, u' =v.

" k\{n-k)\

5".

Приведем некоторые

общие

формулы

для

производных

любого порядка

у^х";

у^"^

=а{а-1)...{а-п

\)х"~".

Если а

-1,

то

nt> (-1)"п! ^ 1 Г 1 1"^ (-1)"(2п-1)!!

I 1 _v '' Если а = — ,то ' ' -^ ^ —

с"*'

A/^J (2JC)"VI

y =

(^a+bx)

(^a,b-const);

/'•^=a{a-l)...{a-n

l)b''{a+bx)'"\

( 1

fj-lfjiW"

bx)"

r 1 t^ _(-!)"

\n+l '

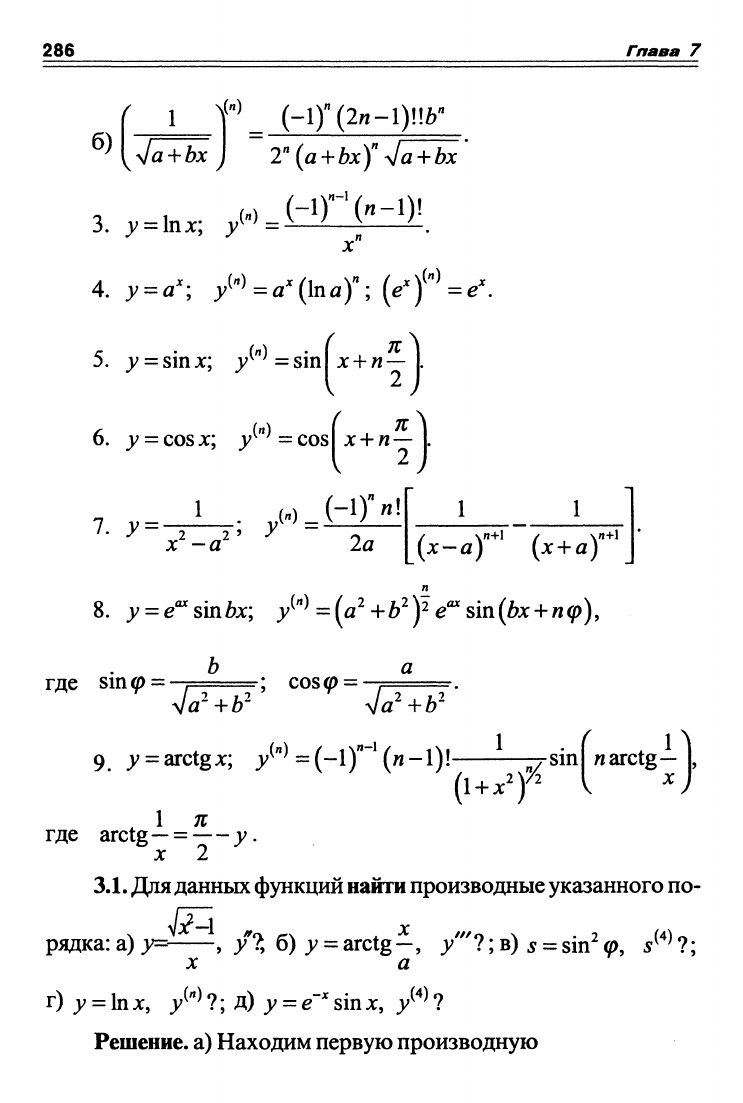
286 Гпава 7

б)

\(''

1 Y - (-l)''(2n-l)!!6''

^la+bx j 2"{a+bx)"y/a+bx'

= sinx;

j;^

=sin

7Г

x + « —

= cosx; у

=cos

x +

n —

1 in) (-1)"'^!

X -a

jc-a) [x

Л+1

e"^sinZ>x;

y''^=(a4fe')2e"^sin(6x +

«<p),

где sin<i[>=: , ; cosip= .- -.

1 /^

. 1 7C

где arctg~- = y,

X 2

3.1.

Для данных функций

найти

производные указанного по-

рядка: а) у= , /?, 6) у

arctg—, /"'?;в) s

sin^о,

s^"^^?;

X а

т)

Injc, у^"Ч; Д) у

в""sinx,

j;^^^?

Решение, а) Находим первую производную

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ 287

1 2хх

•47^\

х'

хЧх^-l'

Вторую

производную находим диференцированием

j''

по

д:

1х'-1-х'

б)

Находим первую производную

1 1 _ а

Дифференцируя у'по

jc,

находим

вторую

производную

„ -lax

У =•

Дифференцируя еще раз по

х,

находим третью производную

(а^+х''\ -Ixia'+x^^lx 2а(Зд:'-аМ

/" = -2а^ Ч —

-^ г^.

[а'+х')"

{а'+х')'

в)

Для нахождения четвертой производной дифференциру-

ем последовательно четыре раза по (р

/ =

2 sin (р

cos

(р

= sin

2(р\

s'' =

2 cos

2ф;

s''

= -4

sin

2ф;

5^^^

= -8

cos

2^.

г) Для нахождения л-й производной дифференцируем пос-

ледовательно заданную функцию до тех пор, пока не выявим

общую

закономерность нахождения последующей производной

1 = х-^ /' = -1.х~^ /"

Ь2х-^ У')=-Ь2.3х-^ ит.д.

288 Гпава

Отсюда

У")

=(-1)""' {п-\)\х-\ (См. 3. пункт 5°).

д) Поскольку функция

представляет произведение двух

функций

^""^;

V-

sin

л:,

то применяя формулу Лейбница

=(wt;f^

=w(% + 4u"V

6uV44uV"+//t;('^

(4),

получим

j;^"^^

в"""

sin

4^"''

cos

бе"""

sin х +

Ае"''

cos

е"""

sin х.

3.2.

Найти

производные указанного

порядка:

а) ^

л-ху=^

у'

б) >^=x+arctg|;

/?;в)

y=jc^-f.3jcv;

/'?; г)

cos(x);) = x';

У'?;

д);сЧ/=1;

/"?;e)x

tg(jc4-;;);

/"?

Решение, а) Дифференцируем правую и левую часть по

е^у'+у

ху'

откуда

у = ;; .

е- +х

Дифференцируем

еще

один

раз

по

„_

у\е^^х)-у{еУу'^\)

Подставляя

последнее выражение значение

у',

получим

у^е'

[е'+х) (е^+лг)

б)

Дифференцируем

обе

части

по

л:

аИФФЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ фУНКиИИ 289

/=1+ ^ У

ц-ы^

Л'

откуда у

,_JA±7

у =

V4+7-1'

Дифференцируем еще раз по х

_2^l4 +

y^ [ 2^4

/ ^

(74^-l)'

(^/4^-l)

в) Дифференцируем правую и левую часть по у

Ъу^

—Ъх^х^-\-Ъ{ху-\гх)^

^—^

х^-^у

Дифференцируем еще раз по у

„_(2j.-x-)(;c'+>.)-(/-j:)(2x»4l)

Подставляя в последнее выражение х', получим

3 •

_2у(х'

у)'-2{/-х){х-+у)-2{/-х)'х

(х'^у)'

г) Дифференцируем обе части по у

sm[xy)[xy + x) = 2xx, откуда х = .

2x + ysin[xy)