Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

480

Гпава 9

Решение, а) По формулам (5) находим координаты центра

. 3jc(l-f9jc') ^ 3 1+9JC' 1 9 2

кривизны кривой <;=

-Уд:

,Т7=7+—~—~^'^~^^ •

Исключаем из этих выражений х. Из первого равенства

имеем х =

-3/—.

Подставляя найденное значение х во второе

выражение, получим уравнение эволюты в явном виде

1 9fti

— . Таким образом, эволютой параболы является

3 2

полукубическая парабола

(рис.

9.5).

Рис. 9.5

б) Уравнение астроиды. Функция задана неявно. Находим

1 1

Гу^

производные: у =

ные в формулы

(5),

получим

уХ

„ 1

^ а' ^

уху^

. Подставляя производ-

Гу\

^ =х

+ -

' а ^

v^'^/

— \-х+Зх^у\

Г1 =

у + 3х^у\

уХ)

Пользуясь уравнением самой астроиды, исключаем из этих

выражений хпу:

ПРИПОЖЕНИЕ аИффЕРЕНиИАПЬНОГО ИСЧИСПЕНИЯ

481

((^

-Г])^ = х^ -

j;^,

((^

+7])^ + (^ -7])^ = 2(х^ + у^') = 2а^\

Если повернуть оси координат на 45° и по формулам

^ ^+7] ^-77

gj = у— , 7] J = - j^ выразить новые координаты

через

ста-

рые,

то уравнение эволюты в новой координатной системе

примет вид ^^/^ +7]j^ = (2а)^

•

Таким образом, эволютой ас-

троиды будет астроида вдвое больших размеров (рис. 9.6) и

с осями, повёрнутыми на 45° относительно старых коорди-

нат.

Рис. 9.6

в) Параметрические уравнения эллипса. Находим производ-

ные:

л:

= - sin

7 =

2 cos /, Jc

= -

cos /,

= -2 sin t. Подставляя в

формулы

(5),

получим

с, sin^/ + 4cos^r ^

с,

=cos^ г r-2cos/ =

2sin / + 2cos t

cos /

cos^

cos ^

= -3

cos^

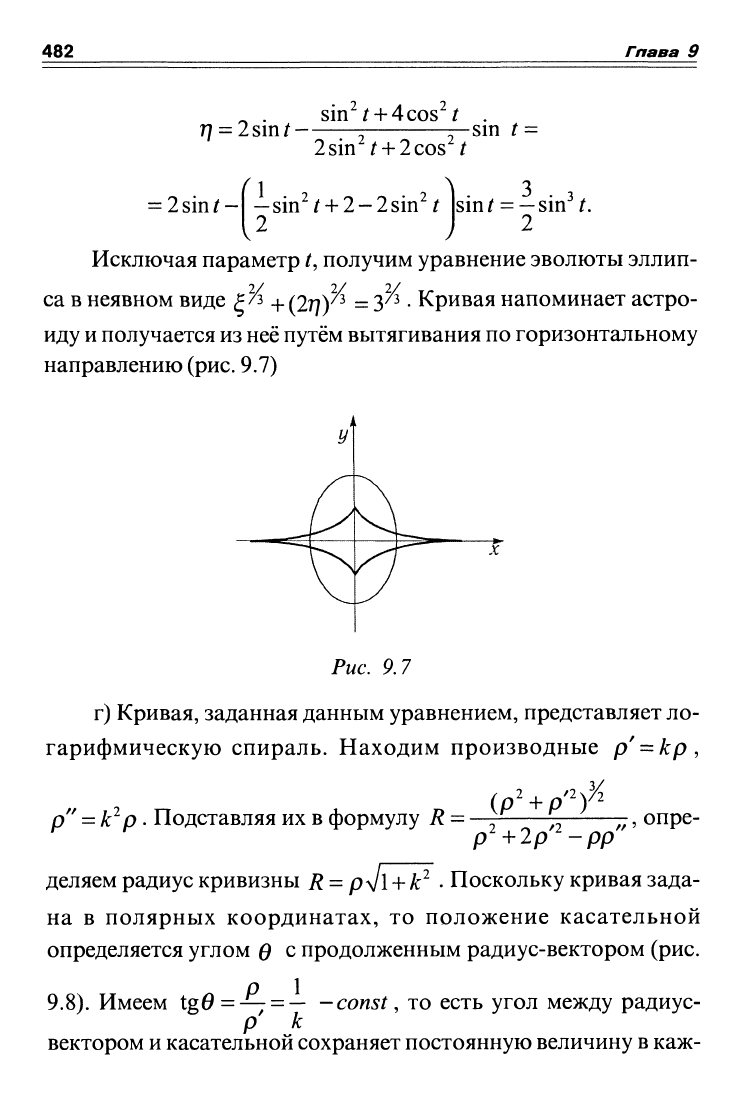
482

Гпава 9

ri =

2smt —:; ^—sm t

sin

/ -

2sin^^ + 2cos^/

sin^ +

2-2sin^

3 . 3

sin/= —sin t.

Исключая параметр /, получим уравнение эволюты эллип-

са в неявном виде £^ + (2т])^ = 3^

•

Кривая напоминает астро-

иду

получается из неё путём вытягивания по горизонтальному

направлению

(рис.

9.7)

Рис. 9.7

г) Кривая, заданная данным уравнением, представляет ло-

гарифмическую спираль. Находим производные р'

кр,

^2чК

:,опре-

р''

к^р

Подставляя их в формулу R

—~- ^

р'+2р''-рр'

деляем радиус кривизны R

р^1

к^

. Поскольку кривая зада-

на в полярных координатах, то положение касательной

определяется углом Q с продолженным радиус-вектором (рис.

9.8). Имеем tg0=-^ =

const,

то есть угол между радиус-

р к

вектором и касательной сохраняет постоянную величину в каж-

ПРИПОЖЕНИЕ аИФФЕРЕНиИАПЬНОГО ИСЧИСПЕНИЯ 483

ДОЙ

точке М кривой. Поскольку

А:

= ctg0 , то радиус кривизны

R и, как следует из

/S.ONM

, совпадает с полярным от-

sin0

резком нормали NM. Поскольку точка

Л/^

является центром кри-

визны, то координаты центра кривизны Pp<Pi

полярной системе

координат

(см.рис.

9.8) примут вид р^= pctgd =кр

,(pi

-(р

Рис. 9.8

Пользуясь уравнением логарифмической спирали, исклю-

чаем р и ^ из этих уравнений, тогда уравнение эволюты при-

мет вид pj =кае ^ л Нетрудно заметить, что уравнение

эволюты также представляет уравнение логарифмической спи-

рали, которая получается из исходной поворотом полярной оси

вокруг полюса на —.

9.4. Особые точки плоских кривых

1°.

Особой точкой М{х^,Уо) плоской кривой

F(X,JH)

= 0

называется такая точка, координаты которой удовлетворяют

трём уравнениям

484

Гпава 9

При исследовании основных типов особых точек вводят

обозначения A^F'^{x^,y^\ B^F^ix^.y^), C

F;^(x,,y,l не

все равные нулю и D

АС-В^,

Если

> О, то

— изолированная точка (рис. 9.9).

М,

Рис. 9.9 Рис. 9.10

Если

< О, то

— узел, т. е.

двойная

точка (рис. 9.10).

Если D-0, то

— точка возврата

первого

рода (рис.

9.11) или второго рода (рис. 9.12) или точка самоприкосновения

(рис.

9.13), или изолированная точка.

Рис. 9.11 Рис. 9.12

Для решения вопроса о виде особой точки необходимо рас-

смотреть расположение точек кривой в окрестности особой точ-

ки.

Угловой коэффициент касательной к кривой в особой точке

может быть найден из выражения Ск^ + 2Вк +

О.

В случае

изолированной точки касательных нет; в узловой точке — две

различные касательные; в точке возврата или самоприкоснове-

ния — одна общая касательная к обеим ветвям кривой.

ПРИПОЖЕНИЕ аИффЕРЕНиИАПЬНОГО ИСЧИСПЕНИЯ

485

Рис,

9.13

2°.

Если кривая задана параметрическими уравнениями

(p{t\y

= \f/{t)

ипри^

^о

x'^=(p\t^)^Q

и У1^\1/ХУ^)^0^ТО

имеет место особая точка.

Пусть хотя

бы

одна

из

производных второго порядка

х^ ,

у^

отлична

от

нуля, например

х^>0,

тогда налицо точка воз-

врата. Если

х^у^-

х^у'^'л-

О,

то

— точка возврата перво-

го рода; если

х^у^-

х^у^'=

О,

то

М^ — точка возврата второго

рода.

случае трансцендентной кривой могут встретиться

дру-

гие виды точек: угловые точки, точки прекращения и т.

д.

4.1.

Выяснить характер особых точек кривой

х^ =

ау^

+ у^

Решение. Обозначим F(x,y)

ах^

-h

у^

-jc^ и

найдём част-

ные производные

-2х,

F^,

lay

Ъу^.

Из решения системы

уравнений

-2JC

= 0,

2а;;+

3/=

О,

находим координаты особой точки 0(0,0).

Для выяснения типа особой точки находим вторые частные

производные в ней

F: = -2- А = -2,

5 = 0,

ху

F';^2a

6y;

2а.

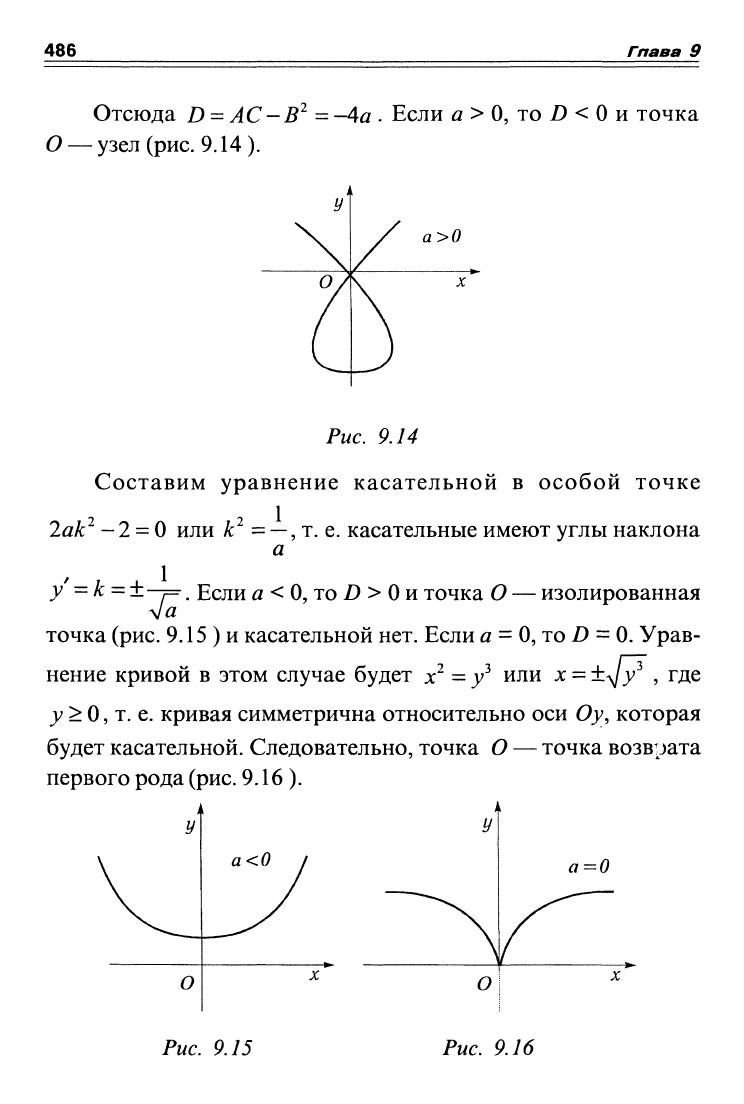
486

Гпава 9

Отсюда D

АС-В^

-4а . Если а>

О,

то

D <

и точка

О — узел (рис. 9.14).

/"".

•

Рис. 9.14

Составим уравнение касательной в особой точке

2ак^ -2 = 0 или

А:^

—,

т. е. касательные имеют углы наклона

-1<^

±—j=.

Если л <

О,

то

и точка О — изолированная

л/л

точка (рис. 9.15 ) и касательной нет. Если

О,

то

= 0. Урав-

нение кривой в этом случае будет х^

у^ или х

±^jy^ , где

J > О, т. е. кривая симметрична относительно оси Оу, которая

будет касательной. Следовательно, точка О — точка возврата

первого рода

(рис.

9.16).

а=0

Рис. 9.15

Рис. 9.16

ПРИПОЖЕНИЕ ПИффЕРЕНиИАПЬНОГО ИСЧИСПЕНИЯ

487

4.2.

Показать, что особые точки кривой

= acos^r,

у^а

sin^

t есть точки возврата первого рода.

Решение. Найдём первые производные

х^''^-За

cos^

sin г,

у[ = 3<2sin^ ^cos^. Приравнивая их нулю, получим четыре осо-

^ я- Ъп

бые точки ^, =0,

-~-> h -^у и

—

•

Вьшислим вторые производные У =

За{2 cos /

sin^

cos^

t),

У = За(2 sin

cos^

t -

sin^

t).

Поскольку в особых точках вторая производная х'/ или у''

отлична от нуля, то налицо точки возврата. Найдём третьи про-

изводные x''' = 3a(7sin^cos^^-2sin^0. y=3a(2cos^^-7sin^^cos0.

Так как в особых точках M.{i

1,2,3,4)

^ТУ\' ^УТ~ 9^^

sin

cos^

t-2

sin^

t){2

sin t

cos^

t -

sin^

t)\

-9a^

(2 cos t

sin^

t -

cos^

/)(2

cos^

t -1

sin^

cos 0| ^ 0,

это точки возврата первого рода. Нетрудно заметить, что за-

данная кривая есть астроида

(рис.

9.17), декартовые координа-

ты точек возврата которой,

(t/,0),(0,a),(-a,0),(0,-a).

соответственно

Рис. 9.17

488

Гпава

9.5. Касание кривых между собой

1°.

Если кривые у - f{x) и

y-g{x)

имеют общую точку

^о(^о'

>^о)

и касательные к обеим кривым в этой точке совпада-

ют, то кривые в точке М^ касаются друг друга. Условие каса-

ния двух кривых в точке М^ имеет вид

Если в точке М^ для функций /(х) и g(x) существуют

производные всех порядков до (w + 1) -го включительно и

выполняются условия /(Хо) =

g(Xo),

/'(Хо) = gVoX

/Vo) = gX^ol - . /^"Ч^о) = г^"Ч^о)' то говорят, что в точ-

ке

кривые имеют порядок касания п. При п>2 кривые

у = Дх) и

= g(x) в точке М^ имеют не только общую ка-

сательную, но и одинаковую кривизну.

Если кривые у

f{x) и y

g(x) имеют общую точку

^О(^ОУУО)

т. е. /(XQ) = g(Xo), а касательные к кривым в этой

точке не совпадают

/(XQ)

^ g(Xo), то говорят, что кривые в точ-

ке

пересекаются.

2°.

Огибающей семейства

плоских кривых называется кри-

вая,

которая касается каждой кривой семейства в одной или не-

скольких точках и причём вся состоит из этих точек касания.

Если уравнение семейства кривых, зависящих от одного

переменного параметра а, имеет вид F(x,

>^,а)

О,

то парамет-

рические уравнения огибающей определяются системой уравне-

ний

F(x,;;,a) = 0; F;(x,j;,a) =

(1)

Исключая из уравнений (1) параметр а, получим уравне-

ние

D{x,y)^0, (2)

ПРИПОУКЕНИЕ аИФФЕРЕНИИАПЬНОГО ИСЧИСПЕНИЯ 489

которое называется уравнением

дискриминантной

кривой.

Дис-

криминантная кривая может содержать геометрическое место

особых точек данного семейства, не входящее в состав огибаю-

щей данного семейства.

3°.

Соприкасающаяся кривая. Пусть дано уравнение кри-

вой y

f{x) и семейство кривых с п параметрами

G{x,y,a,b,... ,/) = 0. Требуется, изменяя знчения параметров,

выбрать из этого семейства такую кривую, которая с данной

кривой в некоторой её точке М^(х^,у^) имела бы наивысший

возможный порядок касания, т. е. найти к данной кривой

у = f{x) соприкасающуюся в точке

кривую.

Введём обозначение Ф{х,а,Ь,... J)

G{x,f(x),a,b,... ,/) и

запишем условия касания

Ф(Хо,л,6, ... ,/) = 0,

Ф'^(х^,а,Ь,

... ,/) = 0, ... ,

Ф[::!\х,,аЛ^^^.1)=о. (3)

Из системы

уравнений

(3) с п

неизвестными находим систе-

му значений параметров а,Ь, ...,/. Таким образом определяется

соприкасающаяся

кривая,

имеющая порядок касания

не ниже

п-1-

5.1.

Найти порядок касания цепной линии у = — (^^ + е"'') с

параболой у

—х^-\-\ в точке х^ = О.

- 1 9

Решение. Обозначим f(x)

—(e''+e "") и g(jc) =

—JC

+1 и

найдём последовательные производные от этих функций

Пх)

^(е'-е-'),

g\x)

Г(х)

^(е'+е-^),

g'Xx)

ГЬ)

^(е'-е-'),

g"Xx)

0,...