Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

460 Гпава 9

Разделив это уравнение на уравнение лемнискаты, полу-

чим

tg0 = -^ = --ctg2(jf), откуда в=—л-2(р.

Если обозначить через аир углы наклона касательной и

нормали к полярной

оси,

то получим

а = 0 + (р=:-

3(р;

^=«-у,

откуда, j8 =

3<р,

т. е. угол наклона нормали к лемнискате равен

утроенному значению полярного угла.

9.2.

Касательная плоскость

и нормаль к поверхности

р.

Касательной

плоскостью

к поверхности в заданной на

ней точке М называется такая плоскость, которая содержит ка-

сательные ко всем кривым, проведённым по поверхности через

эту точку.

Нормалью к поверхности называется прямая, перпендику-

лярная касательной плоскости в точке касания.

Если поверхность задана неявным уравнением F(x, y,z)

то уравнение касательной плоскости в точке М^(х^,у^,2^) име-

ет вид

ах ду OZ

3FO

Э^О dpQ

где —-^, —^, —^ — значения частных производных в точке

ах ау OZ

о;

x,y,z — текущие координаты касательной плоскости.

Уравнение нормали к поверхности будет

ПРИПОЖЕНИЕ аИффЕРЕНиИАПЬНОГО ИСЧИСПЕНИЯ 461

^-^0 _У-У<, _^-2о

ЪР^ ЪР^ ЪР^ (2)

Эх Эу 3z

Вектор ^^"^г-?-^—jT—f называется нормальным векто-

[ Эх Э^; Эг J

ром к поверхности. Если на поверхности есть точка, в которой

дР дР dF ^ ^ . .

— = — = — = О, то она называется особой и в ней нет ни ка-

Эл:

Э;; dz

сательной плоскости, ни нормали к поверхности.

Если уравнение поверхности задано в явном виде

f{x,y),

то уравнение касательной плоскости

z-z,^^{x-x,) +

^{y-y,),

(3)

ох ду

^/о Э/п , ,

где —^, ^^^ — значения частных производных в точке

Эх ду

Уравнение нормали в этом случае

^ ^ -1 • (4)

Эх ду

Направляющие косинусы нормали к поверхности опреде-

ляются выражениями

. -р -q 1

cosA = —. :r; cos/l=—. =•; cosv =

(5)

где p

-:r-

Я-^г--

—7- Двойной знак перед корнем

Эх F, Э>^ Р^

соответствует двум противоположным направлениям нормали.

2°.

Если поверхность задана параметрическими уравне-

ниями

462

Гпава 9

(p{u,v),

\{/iu,v), z

x{u,v),

TO уравнение касательной плоскости в некоторой точке

(xo,3;o,Zo) имеет вид

|^-^о

У-Уь 2-^0

/ / /

\ Уи 2„

/ / /

"^у Уу V

Направляющие косинусы нормали

(6)

cosA =

cos ji

±У1А^+В^+С^' ^""^ ±У1А'+В^+&

cosv =

+л/л'+5'

+ С' '

(7)

где

У«

\Уо

;

2„

^„

; с=

^с

>'с|

А^

3°.

Углом между двумя поверхностями

точке их пересече-

ния называется угол между касательными плоскостями, прове-

дёнными к рассматриваемым поверхностям,

данной точке.

Поверхности назыаются

ортогональными^

если они пере-

секаются под прямым углом

—

в каждой точке линии их пе-

ресечения.

2.1.

Для данных поверхностей найти уравнения касатель-

ных плоскостей и нормалей в указанных точках: а) z = arctg— в

{

точке Mr,

-1;1;~—1;

б) х^+/+z^-jc:V^-10 = 0 в точке

Мо(~1;2;1); в) x = psin(p,

= рсо8ф, z

ptga в точке

^о(Ро'Фо);г) rlucosv, us'mv, ^la^-иЛ вточке r^^ixo^y^.z^}.

ПРИПОЖЕНИЕ аИффЕРЕНиИАПЬНОГО ИСЧИСПЕНИЯ 463

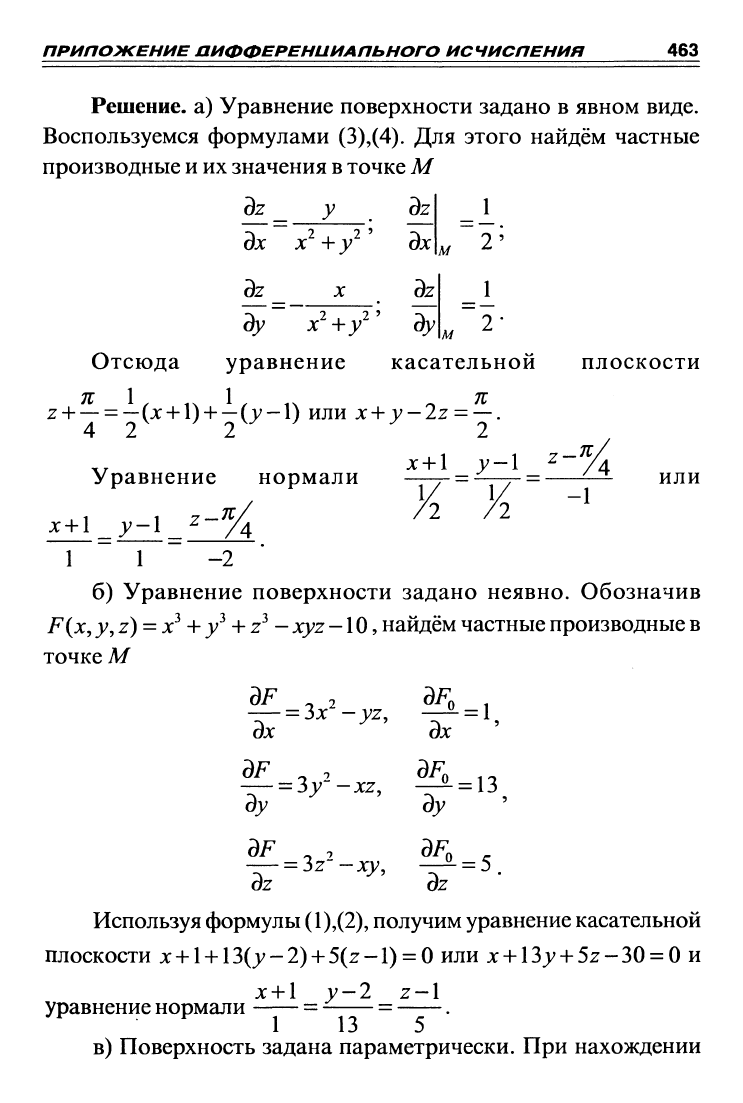
Решение, а) Уравнение поверхности задано в явном виде.

Воспользуемся формулами (3),(4). Для этого найдём частные

производные и их значения в точке М

У ^^

дх X' +

у^

Ъх

dz X д:

ду X +у ду

л."2

Отсюда уравнение касательной плоскости

7г1,

.. 1, .. ^;г

ZЛ = —(jC-f 1) + —(у-1) или X-Vy

—

LZ— — ,

^ 1 1 2

х + 1

у-\ ^-^/^

Уравнение нормали —j-

-—j-

^-^ или

1/1/ -1

x^^y-AJ_^

/2 /2

1 1 -2 '

б) Уравнение поверхности задано неявно. Обозначив

F{x, у, z)

+у^ +z^ - xyz -10, найдём частные производные в

точке М

dF 2 ^^0 1

— = 3х -yz, —^ = 1,

Эх дх

— = 3у -JCZ, —^ = 13

ду ^ ду '

dF 2 ^^0 с

—~

= 3z -ху, -^^ = 5.

dz OZ

Используя формулы

(1),(2),

получим уравнение касательной

плоскости

+ l + 13(>'-2) + 5(z-l) = 0 или x + 137H-5z-30 = 0 и

jcH-1 У--2

—1

уравнение нормали = = .

в) Поверхность задана параметрически. При нахождении

464

Гпава

касательной ПЛОСКОСТИ

точке {pQ,%) воспользуемся уравне-

нием (6). Вычисляя производные

точке

М^,

будем иметь

Z-Z,

sm%

COSCPQ

tga

Pocoscpo -PoSiiKPo

= 0.

ЧИМ

Откуда

при

Posin%,

Уо

Pocos(p^,

z^ =

tga

полу-

xpo sin (p^iga- PI sin^ %^%а

yp^ cos (Potga-

-pl cos'

<Ро

tga - zpo + Po tga = 0

или

sin

%-\-y

cos

фо

ctg a = 0.

Уравнение нормали к поверхности (2) в точке М^ будет и

уравнением нормали к касательной плоскости. Таким образом,

x-ppSincpo ^y-p^cos% ^ z-potgg

sin<pQ cos^o ~-ctgao

По

условию задачи поверхность задана параметрически-

ми уравнениями

х = и

cos

y^usmv,

z- 4й^ -

Для

на-

хождения касательной плоскости

точке {x^^y^-^z^

воспользуемся формулой (6). Находя частные производные

по

u,v

точке

(XQ,

J^O,ZQ)

будем иметь

^-^0

У-У^

cos

sin

-UQ

COS

z-z^

= 0.

Откуда

ПРИЛОЖЕНИЕ аИФФЕРЕНиИАПЬНОГО ИС ЧИСПЕНИЯ 465

(z-ZoKCOS

v^+{y-y^)

J " -f

/ Ч • 2 / Ч t/oCOSt^o _

+(z-Zo)WoSin ^,+(x-Xo)-f==f = 0

или, переходя к координатам

JC,J;,Z

преобразуя последнее выражение к виду

XXQ

j^>^o

ZZQ

>^О

И подставляя вместо квадратов в

правую часть их значения через криволинейные координаты,

окончательно получим хх^ + уу^ -\-zzQ=a^.

2.2.

Написать уравнения нормали к поверхности конуса

х^

у^

z^ в точке

(4;3;5).

какой точке конуса нормаль не оп-

ределена?

Решение. Уравнение поверхности задано неявно. Обозна-

чая F(x, у, z) =

х^

j^^

- z^, находим частные производные

= 2х, = 2у^ =

—2z,

Эх ду dz

^ =

^ = 6, ^ = -10.

Эх ду dz

Уравнение нормали к поверхности конуса примет вид

x-4__j^-3_z-5 x-4_y-3__z-5

^\dF dF ЭFl

Вектор п<—,—' т~

— ^^^^ нормальный вектор к повер-

[

Эх

ду dz ]

хности конуса. Поскольку в точке (0;0;0) производные

466 Гпава 9

dF dF dF ^ , . .

-—

—-=——

О,

то эта точка является особой и в ней нормаль

Эх оу OZ

к поверхности конуса не определена.

2.3.

Найти углы с осями координат нормали к поверхности

х^

+у^ -xz-yz

0 в точке (0,2,2).

Решение. Уравнение поверхности задано неявно. Восполь-

зуемся формулами (5). Найдём сначала частные производные в

точке

Э2_

дх

ду

dF^ Ix-z

dF^ х

у '

Щ _2y-z

3F/

Х +

р=-\\

q = l.

Таким образом, cos

= -^, coSjU =

—1=,

cosv=-j=r.

2.4.

Определить плоскость, касательную к поверхности

х^

+ 2у^ +2^=4 и а) параллельную плоскости x-2y

^ч „x

lv-lz +

б) перпендикулярную к прямой = = .

2 2-1

Решение,

а)

Уравнение поверхности задано

неявно.

Обозна-

чаем F{x, у, z) =

х^

+ 2у^

н-

и находим частные производ-

Э^ . dF . dF ^

ные —- = 2х, -г- = 4у, — = 2z.

Эх ду dz

Воспользуемся условием параллельности касательной плос-

кости

данной плоскости

aF 3F aF

_^__^__Э2_

2х _ 4>; _ 2z

А ~ В " С ™^ 1 " -2 "" Г

Решая эти уравнения совместно с уравнением поверхности

х^+ 2;;^ H-z^ =4 , находим координаты точек касания

МД1,-1Д)иМ2Н,1,-1).

ПРИПО^КЕНИЕ ПИффЕРЕНиИАПЬНОГО ИСЧИСПЕНИЯ

467

Таким образом, касательные плоскости имеют уравнения:

2(x-l)~4(j;

+ l) + 2(z-l) = 0 или x-2j; + z-~4 = 0;

-2(jc + l) + 4(>;-l)-2(z + l) = 0 или jc-2;; + z + 4 = 0.

б) Из условия перпендикулярности касательной плоскости

и прямой имеем

аг ^F aF

dx_

^^3z_ или ^,= 22^=2z

I т п 11-1

Присоединяя к этим уравнениям уравнение поверхности

х^

•\-2у^

+z^ =Л , находим координаты точек касания

4 22^ Г л -^ оЛ

М,

V7'

л/7'л/7

и Л/,

Vv'Vv' V?

Следовательно, касательные плоскости будут:

^ ^ У

прямой

—

^ г. 14 ^ , ^ 14 ^

или

2JC

2V-Z

—р-

= 0, 2x + 2y-z—г- = 0.

V7 л/7

2.5.

К поверхности

jc^

j;^

-3z =

провести касательную

плоскость, проходящую через точку

Л/,

(0,0,-1), параллельно

1 2'

Решение. Обозначим F(x,у, z)

x^ -у^ -3z и найдём час-

г)Р г)/^ г)Р

тные производные — = 2х, — = -2

— = -3

Воспользуем-

дх ду dz

ся условием параллельности данной прямой и касательной

дР dF dF

плоскости —/ +

——m

—-А2

= 0 или 2х-7""3 = 0. Присоеди-

дх ду OZ

468

Глава

няя к этому уравнению уравнение касательной плоскости, про-

ходящей через точку М^

2х{х^

-х)- 2у(у^

-^у)-

3(zj -

или 2JCV2-2/-3Z-3 = 0,

и уравнение

поверхности,

получим систему

2х

—

у-3

x'-r-3z

= 0,

[2x'-2/~3z-3

= 0.

Из решения этой системы находим, что координаты точки

касания раны х

2, у

z = l. Таким образом, искомое урав-

нение касательной плоскости примет вид

4(x-2)-2(>;-l)~3(z-l) = 0 или 4x-2>;"-3z = 3.

2.6. Доказать, что сумма квадратов отрезков, отсекаемых

на осях координат плоскостью, касательной к поверхности

2 2 2 2

х^

+у^ +z^ =а^, равна постоянной величине а^.

Решение. Обозначим F\pc^y^z) = и найдем

частные производные

дх 3 ду 3 dz 3

Уравнение касательной плоскости (1) в произвольной точке

(•^о'Д^о'^о)

примет вид

x/\x-x^)+y/'(y-y^)+z~/'(z-z^)=0

или, если воспользоваться уравнением поверхности

X у Z _ %

v/3

л/З ^/З

•^0

Уо ^0

ПРИПО?КЕНИЕ аИффЕРЕНиИАПЬНОГО ИСЧИСПЕНИЯ 469

Координаты точек пересечения этой плоскости с осями ко-

ординат соответственно равны

х-а'^х\^^

у-сх^У^^

z-a'^z^^

Отсюда сумма квадратов отрезков равна

ЧТО

и требовалось доказать.

2.7. Показать, что поверхности х^

Л-у^

Л-!^

^ах и

jc^

у^

АЪу

ортогональны друг другу.

Решение. Угол между двумя поверхностями по линии их

пересечения определяется углом между соответствующими ка-

сательными плоскостями в каждой точке линии пересечения.

Будем определять положение касательных плоскостей их нор-

малями, тогда угол между поверхностями равен углу между нор-

малями к касательным плоскостям по линии пересечения

поверхностей.

Введём обозначения

F,(x,;;,z)

= x^+У+z^-ах и

(х,

у^

x^ +у^ +z^ -

ЛЬу

и найдём частные производные

/, =—^ = 2х-а, 1^=—^

2х, щ=—^

2у, т^=—^

2у-4Ь,

ах ах су оу

n,=—^

2z, «2=—^ = 2z.

az az

Воспользуемся условием ортогональности

1^2

+ т^т^

н-

«1^2 =

нормалей по линии пересечения повер-

хностей ах = 4Ьу,

2х(2х -а)

2у(2у - 46) + 2z

•

2z =

О,

4x^-2ax +

4/-86y

+ 4z^=0, 4ах-2ах-2ах = 0,

т. е. условие ортогональности выполняется, что и требовалось

доказать.