Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

610 г пава 11

д) Представим исходный интеграл в виде суммы двух ин-

тегралов

Г~ 1пх , г1 1пх - г- 1пх ,

—^—ах= —г ахл-] -т—ах.

Сделаем во втором интеграле замену переменной x = -,

"^ = —Y и воспользуемся свойствами определенного интегра-

ла, тогда получим

lnf-1

р Inx _ fo [ / j J/_ roln/<i/_

filn/flf^_

filnx(ix

Jo jc'+l ^~ Jl Л Y ?'~Ji /'+1" Jo^4l~ Jox4r

Отсюда следует сходимость и данного интеграла.

Глава 12

ПРИЛОЖЕНИЕ ОПРЕДЕЛЕННОГО

ИНТЕГРЛЛЛ К ЗЛДЛЧЛМ ГЕОМЕТРИИ.

МЕХЛНИКИ И ФИЗИКИ

12.1« Общая схема применения

определенного интеграла к вычислению

различных величин

Определенный интеграл широко используется для вычисле-

ния различных геометрических и физических величин. Рассмот-

рим общую схему применения определенного интеграла к

вычислению некоторой величины

в заданных пределах или на

отрезке

[а,Ь],

1°.

а) Заданный отрезок разделим на

промежутков точка-

ми

(З

х^

...

< x„_j <x^=b и найдем длину каждого из

этих частичных промежутков

б) Выберем в каждом из этих промежутков произвольную

точку ^^ так, что

х,^_^

<^^<х,^,

определим соответствующее зна-

чение функции в этой точке f{^j^) и представим приближенное

612 Гпава 12

значение каждого элемента Aw^ в виде произведения

в) Составим сумму таких произведений по всем промежут-

кам заданного отрезка

/(^,)Ах,+/(<^,)Ах,+ ... +/(^„)Ах„=Х/(^*)Д^*.

к=\

Выражаемая этой суммой величина будет тем ближе к ис-

тинному значению

чем меньше каждый из промежутков

Isjc^.

г) Истинная величина

определяется пределом, к которому

стремится указанная сумма, при условии, что каждый из проме-

жутков Ах^ -> О, т. е.

в предложенной схеме определенный интеграл рассматри-

вается как предел интегральной суммы.

2°.

Некоторые величины целесообразнее вычислять посред-

ством определенного интеграла, пользуясь другой схемой.

а) Пусть некоторая часть искомой величины и есть неизве-

стная функция Aw от переменной

которая изменяется в извес-

тном из условия задачи интервале хе {а^Ь\.

б) Представим дифференциал функции du в виде произве-

дения du = f{x)dx, где /(х) — заданная из условия задачи фун-

кция от X.

в) Поскольку дифференциал функции

при dx-^Qn при-

ращение Aw есть бесконечно малые величины одного порядка

малости, то искомая величина и находится интегрированием du

в пределах от х = а до х =

Z?,

т. е.

u =

jfix)dx

ПРИЛОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА

613

1.1.

Найти площадь криволинейного треугольника, ограни-

ченного параболой у

х^, осью Ох и прямой х = 7: а) рассмат-

ривая определенный интеграл как предел интегральной суммы;

б) посредством дифференциала искомой площади.

Решение, а) Разобьем отрезок интегрирования

[0,1]

на

рав-

ных частей точками деления с абсциссами О,—,—, ...,

, 1

п п п

выберем из полученных

частичных отрезков правые концы, т.

е. Xj =

—,

^2 =

—,

... ,х^_, = ,

Jc^

= 1. Длина каждого из этих

п п

частичных промежутков равна Дх^ =

—

2 ^

Так как у

х , то

/(^.)=

,Ях,)

Гол'

K"J

,-,/М

^nV

K"J

и приближенное значение каждого элемента AS^ выразится в

виде произведения

^tV

AS,=

v«y

3 •

и и

Составим сумму таких произведений

^=1 к=\ П П

Пользуясь формулой суммы квадратов целых чисел

2_'?(«

1)(2«

^=1 6

находим

5 =

/..3

п п п

—+—+-

,3 2 6^

1 1 1

-+—+-

3 2п вп"

614

Гпава 12

Искомая площадь определяется пределом при

/Sx^

-^ О, т.

е. при и

—> оо

5 = lim

1 1

- + —

—-

3 2п вп"

б) Для криволинейного треугольника, прилежащего к оси

Ох (рис. 12.1) дифференциал переменной площади S{x)

S^j^^

есть площадь прямоугольника

со

сторонами у и dx,

т.

е.

dS = ydx.

Подставляя сюда значение функции и интегрируя в задан-

ных пределах а

Ь =

\, получим

S = \ х dx =

12.2.

Площадь плоской фигуры

Площадь всякой плоской фигуры в декартовой системе ко-

ординат может быть составлена из площадей криволинейных

трапеций, прилежащих к оси Ох или Оу.

1°.

Площадь криволинейной трапеции

аАВЬ

(рис.

12.2),

при-

лежащей к оси Ох находится по формуле

S={''nx)dx={'ydx. (1)

Ja Ja

ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА

615

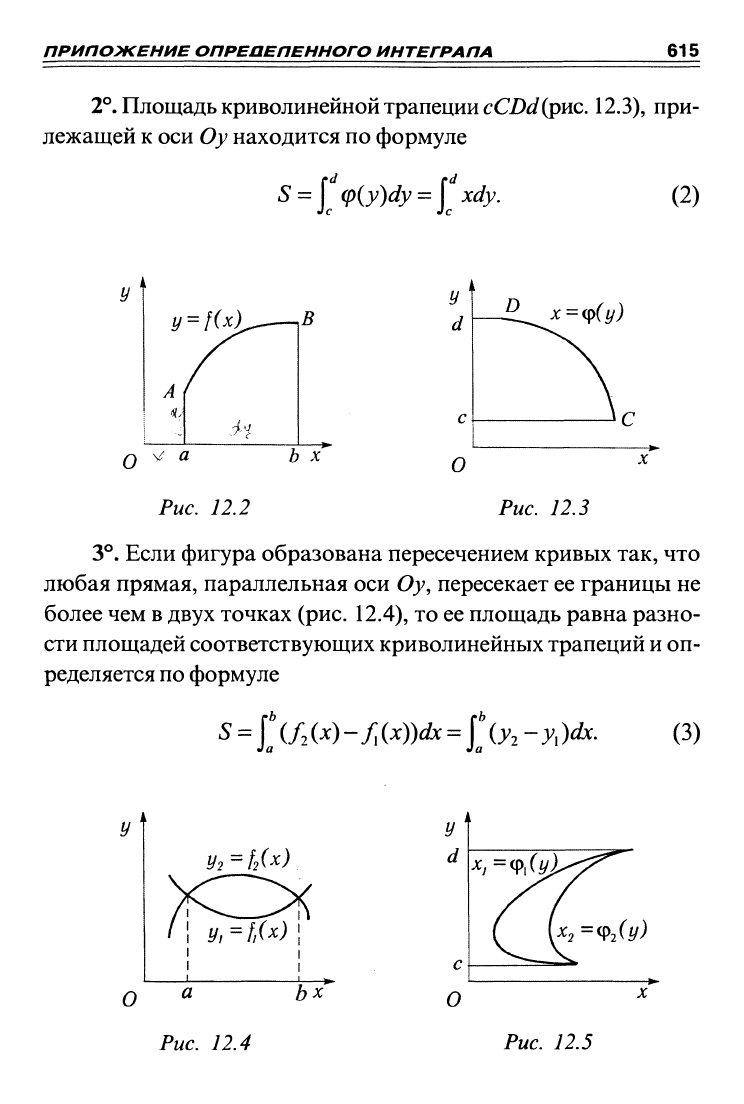
2°.

Площадь Криволинейной Трапеции

сС/)й?(рис.

12.3), при-

лежащей к оси Оу находится по формуле

\(p{y)dy

\xdy.

(2)

у'

-^5^х

<р(у)

У^

Рис. 12.3

3°.

Если фигура образована пересечением кривых так, что

любая прямая, параллельная оси Оу, пересекает ее границы не

более чем в двух точках (рис. 12.4), то ее площадь равна разно-

сти площадей соответствующих криволинейных трапеций и оп-

ределяется по формуле

S=\\Ux)-f,{x))dx=\\y,-y,)dx.

Ja Ja

(3)

У2=!2(х)

y,=f,(x)

О О bx

Рис. 12.4

Рис. 12.5

616 Гпава 12

Если фигура образована пересечением кривых так, что лю-

бая прямая, параллельная оси Ох, пересекает ее границы не бо-

лее,

чем

двух точках

(рис.

12.5),

то ее площадь определяется по

формуле

\\(P2iy)''%(y))dy

[(х, -x,)dy, (4)

4°.

Площадь всякой плоской фигуры в полярной системе

координат может быть составлена из площадей криволинейных

секторов.

Площадь криволинейного сектора ОАВ

(рис.

12.6) находит-

ся по формуле

•'«'I

Рис. 12.6

5°. Площадь криволинейной трапеции, ограниченной кри-

вой, заданной в параметрической форме х

(p{t);

у =

\ff{t),

где

/ 6 [а;

/3]

и ^ (а) -а; (рф)

Ь,

определяется по формуле

S=\''ydx=

[\it)((>\t)dt.

(6)

Ja Ja

2.1.

Найти площадь фигуры, ограниченной линиями:

а)з;

= х

/=9х;б)ху =

= V^,jc = 4, у

0;ъ)х=^-у\

осью ординат и прямыми у

-3; т) у

х^,

у^=-'х;

ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАЛА

617

ji) y=j^,y=x',x=±]:,€) у-хе ^ иееасимптотой;ж) У =x(x--a)^.

Решение, а) Построим графики (рис. 12.7) и найдем точки

пересечения этих

линий.

Для этого решим систему

у^хЛ-1\

|/=9х.

Откуда

(jc

+ Tf

9х или

jc^

5х +

4 =

О.

Точки пересечения

(25 . 5_^3 . ,

x,= —±J 4=

—±—;

X. =4; Х2=1.

Применяя формулу

(3),

будем иметь

у =

+ 2

Рис. 12.7

S=j\-j9x -{x+2)]dx=3fylxdx-j\x+2)dx= 3-jc^-

3 Г ^2 \\

—+2JC

^ '- х'

2х^ 2х

= 2-8-8-8-2 + -+2 = -.

2 2

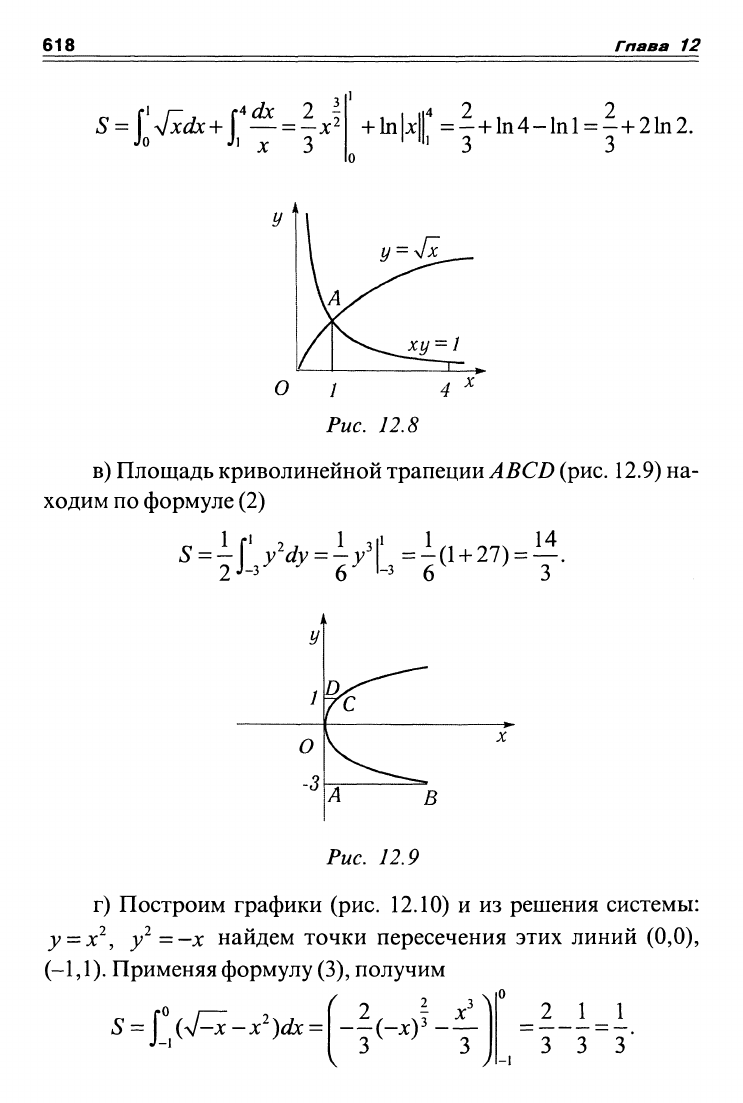
б) Построим графики (рис. 12.8) и найдем координаты точ-

ки А пересечения гиперболы и параболы, решая их уравнения

совместно;

^(1,1).

Поскольку криволинейная трапеция сверху ог-

раничена различными кривыми, то разбивая промежуток интег-

рирования на два промежутка

пользуясь формулой

(1),

получим

618

Гпава 12

S=\

4xdx^\

^dx 2 \

X 3

1пЫГ

=-+1п4-1п1 = -+21п2.

Mil 3 3

О 1

Рис. 12.8

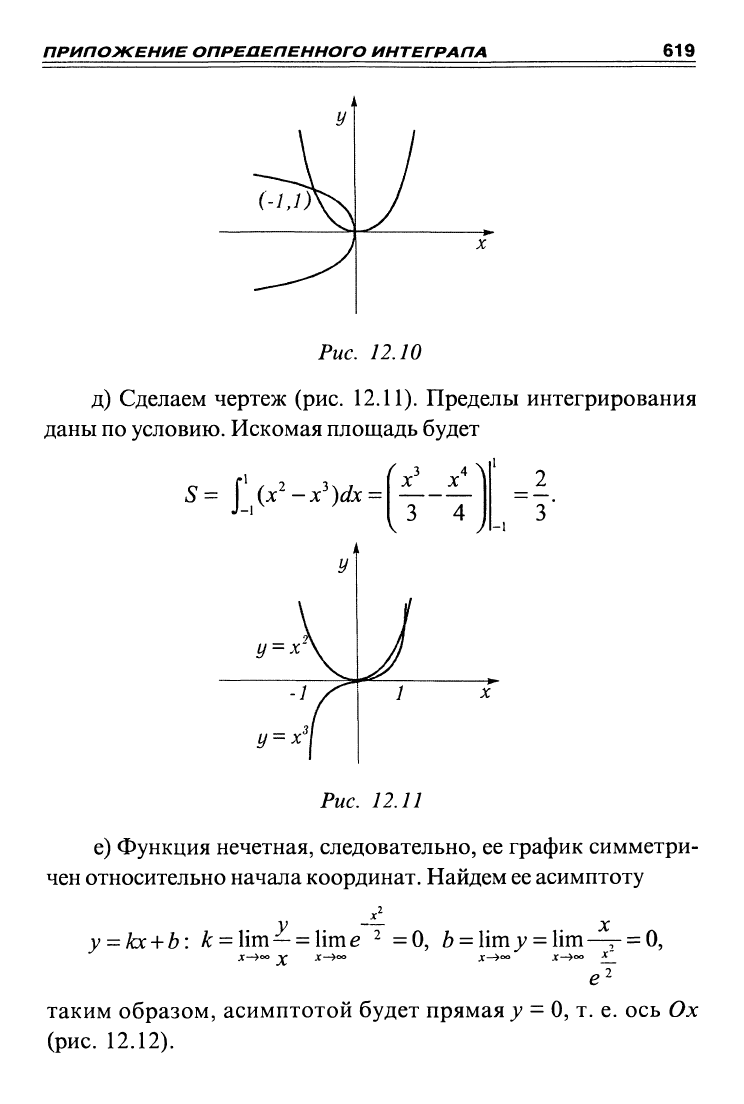
в) Площадь криволинейной трапеции ABCD

(рис.

12.9) на-

ходим по формуле (2)

5 =

—

уау-—у\ = —

+ 27) = —.

Рис. 12.9

г) Построим графики (рис. 12.10) и из решения системы:

х^, у^ =-х найдем точки пересечения этих линий (0,0),

(-1,1). Применяя формулу

(3),

получим

2 1 1

j\yFx-x^)dx-

' 1 '- х'^

-Г.(-хУ -—

3 3 3

ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАЛА

619

Рис, 12.10

д) Сделаем чертеж (рис. 12.11). Пределы интегрирования

даны по условию. Искомая площадь будет

5=1'

(x'-x')Jjc =

/ 3 4 Л

' X X ^

у =

х^

у =

Рис. 12.11

е) Функция нечетная, следовательно, ее график симметри-

чен относительно начала координат. Найдем ее асимптоту

V X

кх-\-Ь:

/: = lim—= Итг ^ =0, 6 =

limj;

= lim—г = 0,

таким образом, асимптотой будет прямая у = 0,т. е. ось Ох

(рис.

12.12).