Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

620

Гпава 12

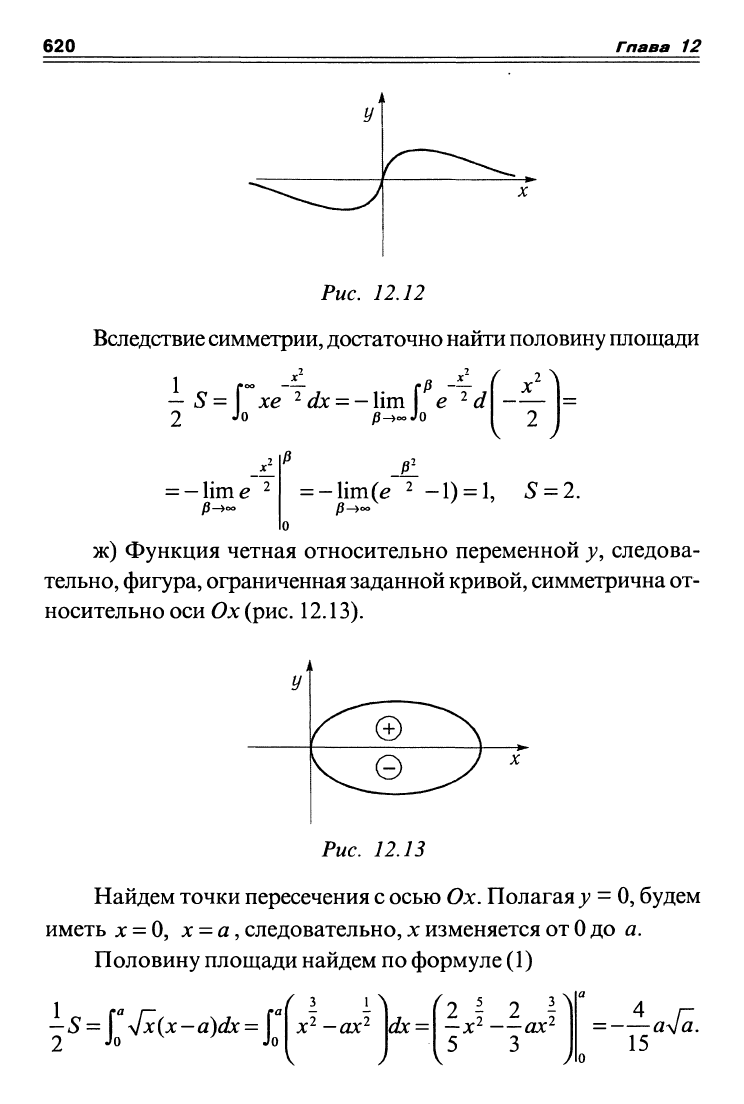
Рис. 12.12

Вследствие симметрии, достаточно найти половину площади

7 ->

—

5 = хе

- lim е

9 Jo

B^ooJo

( х'

= —lime ^

= -lim(e 2 -1) =

5 = 2.

)3—>«>

ж) функция четная относительно переменной ;;, следова-

тельно, фигура, ограниченная заданной кривой, симметрична от-

носительно оси Ох

(рис.

12.13).

Рис. 12.13

Найдем точки пересечения с осью Ох. Полагая

О,

будем

иметь

О,

х-а, следовательно, х изменяется от

до а.

Половину площади найдем по формуле (1)

\ а а( I

— S= I yjx(x-a)dx= I х^

Jo Jo

jc^

-ax^

\dx =

'2 '

~x^

-—ax^

5 3

•- a4a.

ПРИПОЖЕНИЕ ОПРЕЛЕПЕННОГО ИНТЕГРАЛА 621^

Знак минус означает, что фигура расположена ниже оси Ох.

Это,

кстати, следует даже из того, что подынтегральная функ-

ция на промежутке интегрирования отрицательна 4х{х - а) <

при

X 6

[О,

а]. Следовательно, найденный результат надо взять с

противоположным знаком. Таким образом, вся площадь будет

равна 5 = — а4а.

2.2.

Найти площадь, ограниченную: а) эллипсом х

= а

cos t,

у =

sin

б) одной аркой циклоиды

x=^a{t-

sin

а(1

- cos /)

и осью X] в) астроидой

л:

= а cos t, y = as\x\ t; г) кривой

х = 2(^^-1), y

t(4-t^).

Решение, а) Оси координат делят эллипс на четыре одина-

ковые части

(рис.

3.32). Найдем площадь, расположенную в пер-

вом квадранте

1 га

Поскольку эллипс задан уравнениями в параметрическом

виде, то преобразуем интеграл к переменной /. При х =

О,

/ = —,

а при х

а, t

0. Таким образом

( 1 Mi

-каЪ,

S = -4Jja6sin^^J^ = 2aZ?j2(l-cos20^^ =

2aZ?(

^—sin2r

б) При

О,

= 0; при 7 = 0, г-In (рис. 3.67). По фор-

муле (6) имеем

Г2л: ^ ^ - ^2к

5 = 1 ""a^{{-Q.o^ifdt^a^\ "^(l-2cost

cos^

t)dt =

а'

(Ъ 1 Т

-^-2sinr

-sin2r

4 jL

622

Гпава 12

в) Оси координат делят астроиду на четыре одинаковые ча-

сти

(рис.

7.63). Найдем площадь, расположенную в первом квад-

ранте. При х =

О,

/ =

—;

при у-^,

О.

Отсюда по формуле (6)

вся площадь будет равна

3a^sin^t

cos^

tsintdt=-a^\^{\-cos2t-

cos^

2t+cos^

2t)dt =

2 \ ^1

o"2

2 (1

- COS At)dt+-

- sin' 2t)d

sin

r) Найдем точки пересечения кривой с осями координат.

Если

О,

то

±1;

если

О,

то

О,

±2. Отсюда полу-

чим следующие

точки:

при / = -1

(О,

-3), при t

\ (0,3); при

= 0 (-2,0); при

= ±2 (6,0).

Если t

[-2,0], то ;; < 0; если

[0,2],

то у >

О.

Точка (6,0)

является точкой самосопряжения кривой. Следоватльно, кривая

имеет форму петли (рис. 12.14).

Рис. 12.14

Вследствие симметрии фигуры относительно оси х, доста-

точно найти половину площади; тогда вся площадь по формуле

(6) будет равна

ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАЛА

623

S-^2\\{A-t^)Atdt--%\\At^-t^)dt

= %

V 3 5

5 \

512

15 '

2.3.

Найти площадь, ограниченную

линиями:

а) одним вит-

ком спирали Архимеда р

а(р;

б) кардиоидой р = a(\

cos(p);

в) лемнискатой (х^+у^У =2а^(х^-у^); г) окружностями

p=acos(p и р

л/Заsin(р; д) х^ +у^ -Ъаху =

(декартовлист).

Решние. а) Один виток спирали Архимеда (рис. 3.58) опи-

сывается концом полярного радиуса при изменении полярного

угла

(р

от

до

2л:.

По формуле (5) находим

1 f27r 2 2 I ^ ЗР^ 4 3 2

-ГаУс1(р

—(р\

Jo ^ ^ 6 '^

2 Jo • ' 6 ' 'О 3

б) Поскольку кардиоида симметрична относительно поляр-

ной оси (рис. 3.61), то достаточно найти половину ее площади,

когда полярный угол (р изменяется от

до л:. Отсюда по фор-

муле (5) имеем

2'-\

a^{\

cos(pfd(p

a^\ (l

2cos(p^- — (l

+ cos2(p))d(p

2 Jo

^3 1

(p +

2sm(p

+—sm

2(p

3 2

—яа .

в) Лемниската симметрична относительно координатных

осей и делится ими на четыре равные части (рис. 3.62). Если пе-

рейти к полярным координатам х

cos

(р,

р sin

<р,

то урав-

нение лемнискаты в полярных координатах примет вид

р^

=2a^cos2(p.

Четвертой части площади соответствует изменение поляр-

ного угла от

до —. Отсюда вся площадь по формуле (5) будет

равна

624

Гпава 12

1 /

г) Решая совместно уравнения окружностей, находим точ-

ку (рис. 12.15) их пересечения А

а-

л/з к

2 6

равна сумме площадей двух сегментов ОБА и ОСА.

Искомая площадь

Рис, 12.15

Дуга ОСА описывается концом полярного радиуса боль-

шой окружности при изменении полярного угла <р от

до —,

следовательно

SocA

= ^ \^ За' sin'

(pd(p

-a^

J^**

cos 2(p)d(p

1 > 3 2

=—a

(л S]

6 4

^ J

= — a (p—sin2^

Дуга ОБА описывается концом полярного радиуса мень-

к к

шеи окружности при изменении

<р

от

—

до

—,

следовательно,

6 2

1 СЛ 2„„2„л„_а' fA,

SoBA

и «'cos'

(pdcp

= =- К'

cos 2(p)d(p

2Vb

^Уб

ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАЛА

625

(р

+—sin2(p

3 4

Таким образом, искомая площадь

^ - ^осА + ^овА -'

5к

-Si

д) Переходя к полярным координатам x = pcos^,

psin(p в уравнении декартова листа, получим

За sin

ф cos ф

р = —г—

г^—.

Так как петля кривой соответствует измене-

sin

(р

cos (р

нию полярного углаф от

до

—

(рис. 12.16), то площадь будет

равна

^ 1 г^ 9a^sin^(Z)cos^(p ,

5 = -

г ^ , \ d(p.

2-^0 (sin> + cos>)^

Деля числитель и знаменатель на cos^ (р, получим

9 ,ttgVtg£

3^^f^(l

tg» 3 , 1

Ь= — а

г—т

=—а г—- =—а

9 J П

to^

т\^ 9 i (^л. \о^ т\^ 9

14-

2 J(l

tg»^ 2 J(l

tg»^ 2

tg>

Ъа"

Рис. 12.16

626 Гпава 12

12.3.

Объем тела

1°.

Объем тела по площадям его параллельных сечений.

Пусть известна площадь S{x) любого сечения тела плоскостью

перпендикулярной оси х (рис. 12.17). Если х — расстояние сече-

ния от начала координат, то при изменении х на величину dx

диф-

ференциал объема тела равен объему прямого цилиндра с

высотой dx и площадью основания S{x) , т. е. dV = S{yi)dx .

Объем всего тела выражается интегралом

V^^ S{x)dx, (1)

где а,Ъ — левая и правая границы тела

Рис. 12.П

2°.

Если тело образовано вращением вокруг оси Ох криво-

линейной трапеции

аАВЪ

(рис.

12.18), то любое его сечение, пер-

пендикулярное к оси Ох, будет круг, площадь которого равна

ку^. Объем тела вращения вычисляется по формуле

V^n^ y'dx, (2)

Рис. 12.18

ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА 627

Если тело образуется вращением криволинейной трапеции

вокруг оси Оу (рис. 12.3), то объем тела находится по формуле

^п\\Чу, (3)

где с и

й?—

ординаты границ тела.

Если тело образовано вращением вокруг оси Оу криволи-

нейной трапеции

аАВЪ

(рис.

12.2),

то элемент объема равен объе-

му тела, образованного вращением вокруг оси Оу

прямоугольника со сторонами

y^^dx^^

отстоящего от оси Оу на

расстоянии

Объем тела вращения в этом случае равен

2K\ xydx. (4)

В более общих случаях объемы тел, образованных вра-

щением криволинейных трапеций, ограниченных кривыми

У\ = /i (^) ^ Уг- fi (^) ' ^с-^и /j (х) < /2 (jc)

и прямыми х-а,

х = Ь, вокруг координатных осей Ох.Оу, соответственно

равны

b b

V,^it\{yl-yl)dx

V^=2n\x{y,-y,)dx.

(5)

а а

Если кривая задана параметрически,

то,

приведенных фор-

мулах вычисления объема тел вращения, следует сделать соот-

ветствующую замену переменной интегрирования.

3°.

Если криволинейный сектор вращается вокруг полярной

оси и ограничен кривой р

р((р) и лучами<р = а ;(р =

, то

объем тела вращения определяется по формуле

2 ^

V =

—7i\

р^ sin

(pd(p.

(6)

3 „

71]

p''sm(pd(p.

2 2 2

X У Z

а^ b^ г

3.1.

Найти объем трехосного эллипсоида -у

"т

"Т ^

^ •

628

Гпава 12

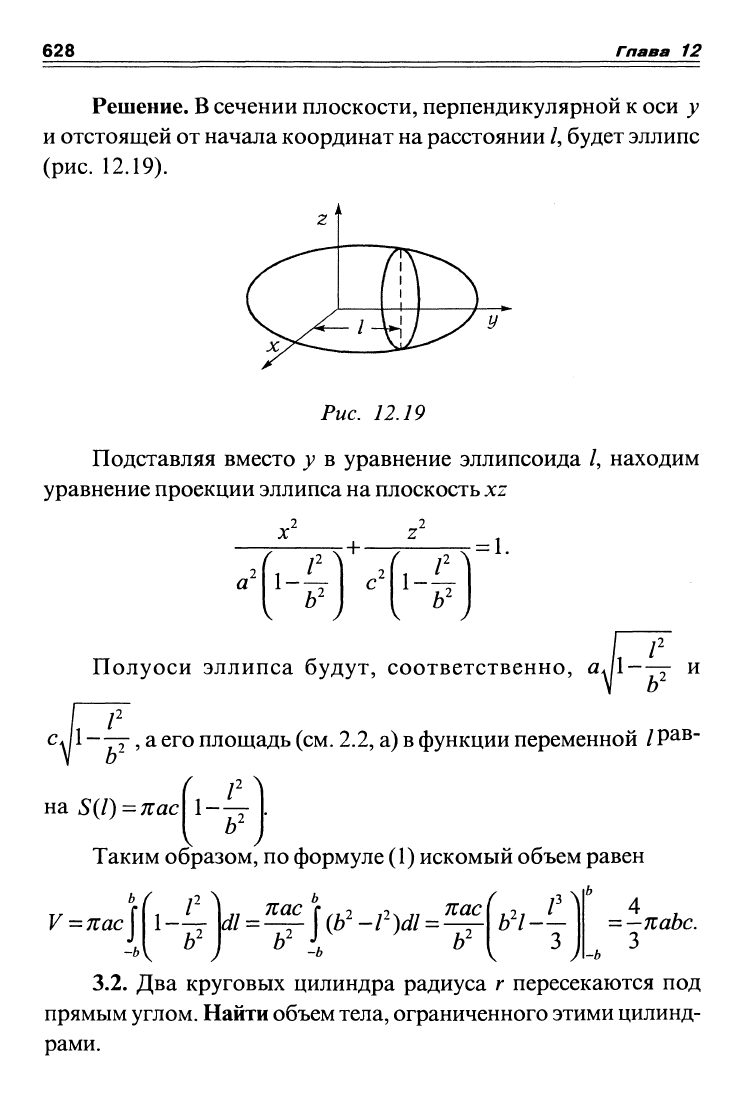
Решение.

сечении плоскости, перпендикулярной к оси у

и отстоящей от начала координат на расстоянии /, будет эллипс

(рис.

12.19).

Рис. 12.19

Подставляя вместо у в уравнение эллипсоида /, находим

уравнение проекции эллипса на плоскость xz

( ^2^

v'-^^

\j-^

V *%

= 1.

Полуоси эллипса будут, соответственно, аЛ\—т- и

с^\\-—,

а его площадь

(см.

2.2, а) в функции переменной /рав-

на

S{1) =

кас

I ,.\

Таким образом, по формуле (1) искомый объем равен

= nac

-Ь\

'^ J " -b

пас

-b

-—каЬс,

3.2. Два круговых цилиндра радиуса г пересекаются под

прямым

углом.

Найти объем тела, ограниченного этими цилинд-

рами.

ПРИПО?КЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА

629

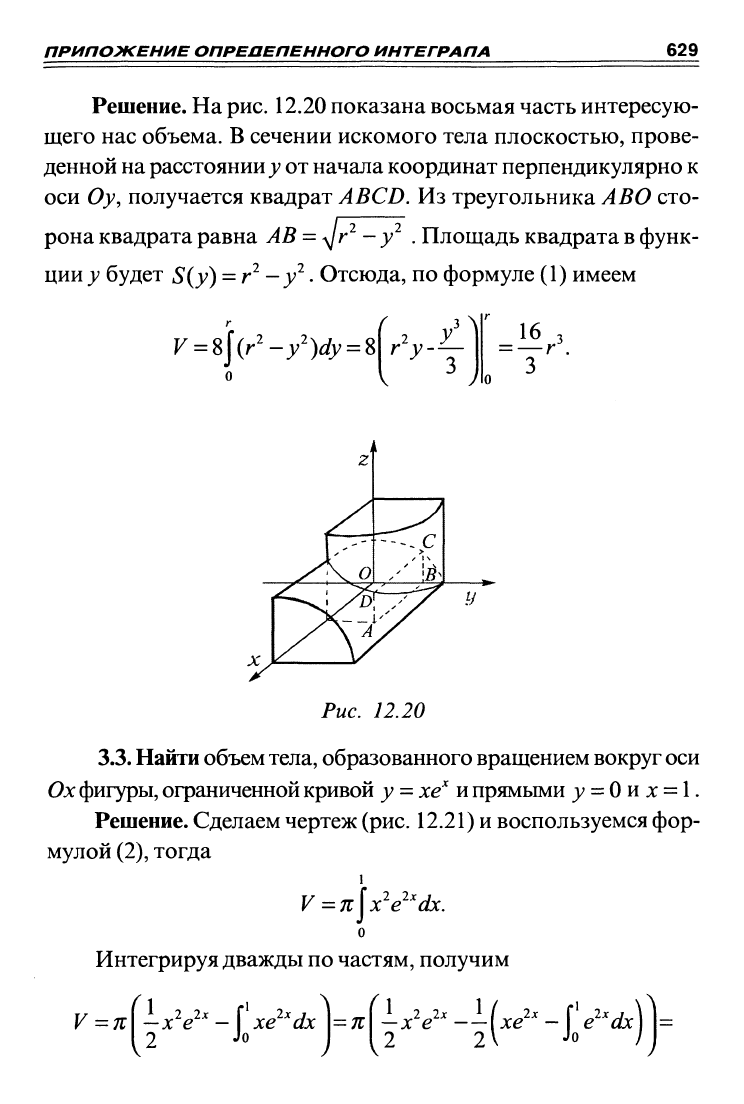
Решение. На

рис.

12.20 показана восьмая часть интересую-

щего нас объема. В сечении искомого тела плоскостью, прове-

денной на расстоянии у от начала координат перпендикулярно к

оси Оу, получается квадрат А BCD. Из треугольника А ВО сто-

рона квадрата равна АВ

yjr^

- у^

Площадь квадрата в функ-

ции у будет S(y)

г^ -у'^. Отсюда, по формуле (1) имеем

у-=^—

. 3

V )

Рис. 12.20

3.3.

Найти

объем

тела,

образованного вращением вокруг оси

Ох

фигуры,

ограниченной кривой у

—

хе" и прямыми y

Oii х

—

Решение. Сделаем чертеж

(рис.

12.21) и воспользуемся фор-

мулой

(2),

тогда

V=n]x'e"'dx.

Интегрируя дважды по частям, получим

•

-х'е'"

-i:

хе dx

^=;rf-xV^

•-1хе^''-^Учх]