Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

640 Гпава 12

Рис, 12.31

Найдем точки пересечения с осью Оу: при

О,

у=^±3.

Вследствие симметрии кривой относительно оси Ох достаточно

найти половину длины заданной

кривой.

Используя формулу

(1),

будем иметь

Интегрируя по частям фл-4у^ =и, dy

dv;

, 4ydy

du -

—,

, v

у, получим

^L=:yyll +

4y'f '•\'^-^4y'dy-hf-j=^

Отсюда

1 =

j;^l

+ 4/ +-1п|2>; +

д/1

+ 4/|| =3л/37+-1п(6 + л/з7).

2 I 11о 2

г) Сделаем чертеж (рис. 12.32) и найдем точки пересечения

окружности и параболы.

Для этого решим систему

у'^

=х^, х^

—6х +

у^ =0- Абсцис-

сы точек пересечения будут

и 2.

Вследствие симметрии достаточно найти половину длины

дуги. По формуле (1) имеем

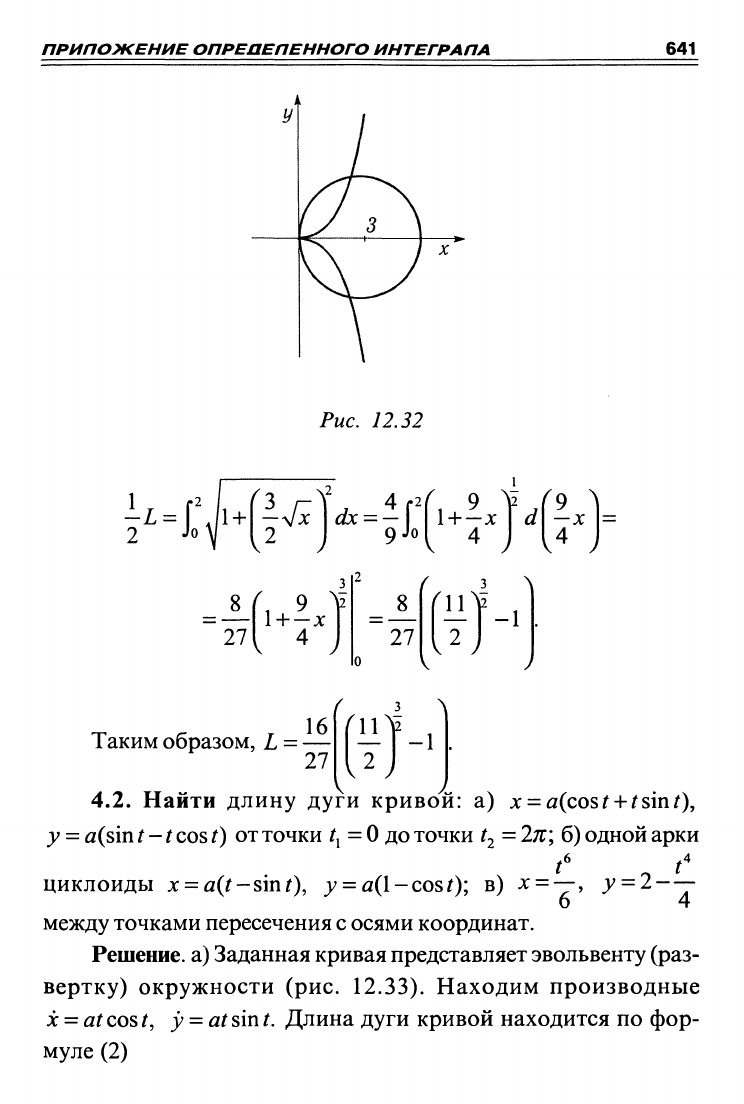
ПРИПО?КЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА

641

Рис. 12.32

i-r/

4r2f^

V /

v4 у

8 Л 9 "t

+ -;с

V2y

-1

Таким образом, L =

•1

4.2.

Найти длину дуги кривой: а) x = fl(cos/

/sinO,

у = a(sin t-t

cos

/) от точки

до точки /j =

2л:;

б) одной арки

ЦИКЛОИДЫ x = a(t-smt), y = a(l-cost); в) х

=—^

= ^—7

6 4

между точками пересечения с осями координат.

Решение, а) Заданная кривая представляет эвольвенту (раз-

вертку) окружности (рис. 12.33). Находим производные

cos

at sin

Длина дуги кривой находится по фор-

муле (2)

642

Гпава 12

Рис. 12.33

L= \ ""yla^t^cos^/ + aYsin^tdt

a\ ''tdt =

Jo Jo

^lair

6) Здесь t изменяется от

до In (рис. 3.67). Находим произ-

водные i =

а(1

cos

О,

у-а sin t. Длина одной арки циклоиды

по формуле (2) равна

i = J

^а^

- cos tf

а?-

sin^ tdt

a л/2 f

yjl

- cos tdt =

C^Tt

t t\

= la sin — dt

--4a

cos —

Jo 7 7

2л:

= 8a.

2 2L

в) Найдем пределы интегрирования: при

О,

/ = 0; при

О,

= л/8

Вычисляя производные x

t^, y

-t^ и исполь-

зуя формулу

(2),

находим

Jo Jo А JO

= -(/"+1)2

3 '

4.3.

Определить длину дуги кривой: а) первого витка спи-

рали Архимеда р

а(р;

б) кардиоиды р =

0(1

+cosф);

ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА 643

_ • 3 ф

в) р - « sin —;

г)

логарифмической спирали р =

ае"^"^

(т

0),

находящейся внутри круга р

а.

Решение. а)Длина дуги первого витка

(О

< ^ < 2л:) спирали

Архимеда (рис. 3.58) определяется по формуле (3) и равна

= J

'^^j{a(pf

-{-a^d(p

ci\''y]l

(p^d(p.

Интегрируя

по

частям

(р-=и, d(p

= dv;

(р-'^->

(pdcp

аи

—

I , получим

Vi+(p'

L = a

откуда

\(рф +

(р^\

-{^"^

(p^d(p

+ \nl(p +

+ (p^\

1о •'О \ /|о I

L= -((pyjl+(p^ +ln(^+^l+(pMj =ал:^11+4л^ +-1п[2л:+л/1+4л:Ч.

б) Вследствие симметрии кардиоиды относительно поляр-

ной оси (рис. 3.61) достаточно вычислить половину ее длины.

По

формуле (3) имеем

= 2 Г

-yja^

(14-

cos

(pf +

а^

sin^

(pdcp

2 V2a

yJl-\-cos

(pdcp

= 4ci\

COS—d(p

Sa sin

:^<P

8a.

в) Изменяя

от

до Зл:, получим кривую (рис. 12.34).

На-

, .

ходим,

что р

=asin —cos—. Отсюда

по

формуле (3) имеем

\""Aa^sm^

—

a^sm^—cos^—d(p=^a\

""sin —1/© =

к \ 3 3 3J« 3

_ ^

""2 Jo

2(р^

а( 3.2^

1-C0S—^

к/ф =

—

<j9—sin—^

3 j 2\^ 2 3 ^

Зя

= — ак.

644 Гпава 12

Рис. 12.34

г) При ^ =

из уравнения логарифмической спирали нахо-

дим, что р

а.

Следовательно, (р изменяется от ~оо до 0. Представим ло-

гарифмическую спираль и круг р = л на

рис.

3.60. Находим про-

изводную р' =

ате"''^.

Длина дуги логарифмической спирали, находящейся внут-

ри круга, по формуле (3) равна

L=f yJa'e'^+m'aV'^d(p = ayJ\+m^f e^d(p

= ayjl

Km —

f%'"^rf(m(p)

= —л/l + m' lim e"4'

=—л/l

+ m'.

4.4.

Найти длину дуги пространственной кривой: а) одного

витка винтовой линии x = acos^ y

asint,

ct;

6) y

-\nx, z

—

от

x=^\ Л0 x

Решение, a) При изменении

от

до 2я получим один ви-

ток (рис. 4.20). Находим производныеx

-asmt,

аcost,

c, Длина дуги по формуле (4) будет равна

6) Запишем уравнение пространственной кривой

парамет-

рическом виде. Пусть x

t, тогда y

— mt, ^ =—; при

ПРИПО^КЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА

645

х =

\\ при х = 2,

Найдем производные i = 1,

= — Г,

и воспользуемся формулой

(4).

Тогда

^=f^R^^^=i

2л/4гЧ4^Ч1

..=j;

2^J

= -(/Ч1пО[ =-(3 + 1п2).

12.5.

Площадь поверхности вращения

Если поверхность образована вращением дуги АВ плоской

кривой у

f(x) вокруг оси Ох (рис. 12.35), то площадь поверх-

ности, образованная вращением дуги, определяется по формуле

гЬ

гь I гт

(1)

Ja Ja

При вращении дуги вокруг оси Оу (рис. 12.3) площадь по-

верхности вращения определяется по формуле

2nf xdl

2л:

J^ xyjl

ixfdy, (2)

Если дуга задана параметрически уравнениями х

x{t),

у = y(t), а < / < j8 , то площадь поверхности вращения вокруг

оси Ох равна

Рис. 12,35

646 Гпава 12

lK\%{t)^{x{t)fHmfdt. (3)

Если дуга кривой задана в полярной системе координат

р{(р), а<(р<р, то

271

f psm(p J

р^

(pyd(p. (4)

Если дуга кривой вращается вокруг произвольной оси, то

площадь поверхности вращения определяется по формуле

2лСксИ,

(5)

где R — расстояние от произвольной точки кривой до оси вра-

щения; dl — дифференциал дуги; а, b — пределы интегрирова-

ния, соответствующие концам

дуги.

Здесь

R и (i/следует выразить

через переменную интегрирования.

5.1.

Найти площадь поверхности, образованной вращени-

ем:

а) цепной линии y

ach— вокруг оси Охот х

0 до х

а;

х'

у'

б) эллипса

—г +

—г =

вокруг оси Ох и оси Оу; в) петли кривой

а b

9ау^

х(За-хУ-

вокруг оси Ох и оси Оу,

Решение, а) Поверхность, образованная вращением дуги

цепной линии вокруг оси Ох показана на рис. 12.36. Находим

производную y'

sh— и значение Jl

iy'^Y =ch—. Тогда по

формуле (1) имеем

= 1K['ach^—dx =

na['\ ch—+1

1^2 a

2x ^

жа\

—sh—+x

яаП -sh2 + l

ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА

647

Рис. 12.36

б) Пусть эллипс вращается вокруг оси Ох, причем а>Ь,

тогда J =Ъ —1-х, уу

=—1--^-В^спо-^ьзуемся

формулой (1)

а а

и найдем подынтегральную функцию

\ а а

b \ 1 а —Ь 9 b r~f 7~т

-—х"- ^—sja -е х\

''-аГ

где а -Ь =с ,

— =

£ — эксцентриситет эллипса. Таким об-

разом,

5 = 2л:Г yla^-£^x^dx

4n-r^la^-£^x^dx.

J-a п

Интегрируя по частям:

yja^

-е^х^ =w, dx

dv;

-£ xdx

= du, x

v, имеем

£X

—xyja -£ X H arcsin

2 2£ a

-1к—\а4а^-£^а^

H-a^ агс8тг| =

2л:/?(6

+—arcsin£).

a\ f £

648

Гпава 12

Если эллипс вращается вокруг оси Оу, то пользуемся фор-

2 « 2

мулой(2):х =а —r-v , хх' = —jy.

хфНхУ

=^x'Hxx'f

=f'-f^/+^/ =

=-J64

y=f>^+^/^

« f'' /1.2 , c' ..2

^ =

2^lLr-^77^^^-

6 J-*

Интегрируя no частям: Jb +-^у =u, dy

dv;

du =

_ 6

гУ^У

^ , v=y, получим

b'+Tl/

,2 c' , b'

2 V b^ Ic

с ,2^2

\Л

—

2ка

л/^Ч7^1п^

^^г^с

2с Tfe'+c^-c

, ^2

Так как 6 + с = а, с = га, то окончательно имеем

S^lKa

b^ , а

£а

lea а-га

2ка

\ +

lea \-е

в) Петля данной кривой описывается текущей точкой при

изменении х то

до

Ъа

(рис.

12.37). Дифференцируем уравнение

ПРИПОЖЕНИЕ ОПРЕОЕПЕННОГО ИНТЕГРАПА 649

кривой

Ыуу'

(За -

jc)'

1х{Ъа

х),

у/

(3^ ^К^ ^) д

1ЛЯ

6а

нахождения площади поверхности, образованной вращением

петли вокруг оси Ох, преобразуем формулу (1)

Рис. 12.37

(За-хУ(а-хУ

= — (За-х)л/а +2ах

х dx

— (За +2ах-х )dx =

' х'^

о 2 , 2 -^

За хЛ-ах

За

= 37Га'

5.2.

Найти площадь поверхности, образованной вращени-

ем:

а) астроиды х

= а

cos^

t, у

= а

sin^

t вокруг оси Ох; б) одной

арки циклоиды x

a{t- sin t), y

a(l-

cos

/) вокруг ее оси сим-

метрии.

Решение, а) Вследствие симметрии астроиды относительно

координатных осей, достаточно найти площадь поверхности,

описанной дугой астроиды, лежащей в первом квадранте

(О

—).

Воспользуемся формулой (3). Вся площадь враще-

ния будет равна