Черненко В.Д. Высшая математика в примерах и задачах (том 1)
Подождите немного. Документ загружается.


630 Гпава 12
х'-х-\-—
\е
4
Рис. 12.21
3.4.
Найти объем тела, образованного вращением вокруг
оси Оу фигуры, ограниченной кривой
j;^
= 4х и прямыми х = 0
иу = 4.
Решение. Сделаем чертеж
(рис.
12.22) и воспользуемся фор-
мулой
(3),
тогда
V
=
n \\xdx = 2я:;с^Г = 32к,
Jo 10
3.5.
Найти объем кольца (тора), образованного вращением
окружности х^ + (;; -4)^ = 9 вокруг оси Ох.
Решение. Центр окружности сдвинут на четыре единицы
вверх, а радиус окружности равен R
= 3
(рис.
12.23).
Решая урав-

ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАЛА
631
нение окружности относительно;;, находим уравнение верхней и
нижней дуги полуокружности
j^,2
=4±v9-x^ .Объем тора пред-
ставим как разность тел вращения, ограниченных этими окруж-
ностями. Учитывая симметрию относительно оси
Оу,
будем иметь
V^2к\\у^,
-yl)dx--2K^\25-x'л-%49^-
-25
+
8л/9-х' +x')dx
=
\6K^^y}9-x^dx.
Рис.
12.23
Сделаем замену:
х =
3 sin /,
Jx =
3 cos
tdt\
при x =
О,
/ = 0;
при
X
=
3,
t-
— .
Тогда получим
Уг.
V
=
\6ку^9со^'
tdt
=
12KY\\
+
co^2t)dt
=
(
=
12к
/
+—sin2r
2
\
=
36л:'
3.6. Найти объем тела, образованного вращением вокруг
оси Ох фигуры, ограниченной полуокружностью
х^
-\-
у^ =\ (при
X
>
О) и параболой
;; =
—х.
Решение. Сделаем чертеж (рис. 12.24)
и из
решения системы

632 Гпава 12
2 3
найдем абсциссу точки пересечения кривых: 2jc^
н-Зх-2
= 0;
1
-3±л/9 + 16 -3±5
^-1,2
х =
Pwc.
12.24
Поскольку криволинейная трапеция, которая вращается
вокруг оси Ох, ограничена различными кривыми, то, вычисляя
объем тела вращения по формуле
(2),
представим его в виде сум-
мы двух интегралов
У
=
я\ y^dx
=
ny—xdx^'Ku{\-x^)dx
= K
+ 7r
10
J Л
X —
ГЗ
1
, 1 1 \\
=
к\ —+1
+
—
^28 3 2 24j
19
= —к.
48
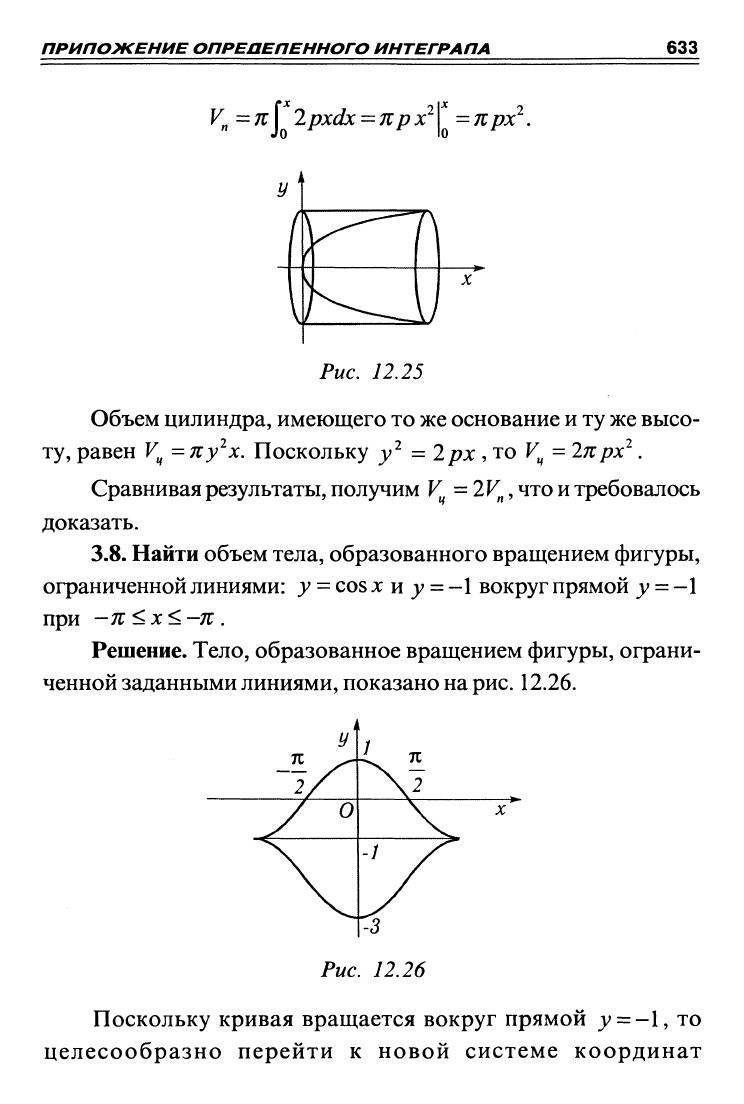
3.7. Доказать, что объем параболоида вращения равен по-
ловине объема кругового цилиндра, имеющего то же основание
и ту же высоту.
Решение. Считаем, что параболоид образован вращением
параболы у'^ =2рх вокруг оси
OJC,
причем сечение возьмем в
произвольной точке с абсциссой х (рис. 12.25). Тогда его объем
равен
ПРИПО?КЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА
633
К„=л:Г
2рх(1х =
прхЛ =крх^
Рис. 12.25
Объем цилиндра, имеющего то же основание и ту же высо-
ту, равен
V^
=
ку^х. Поскольку у^ =2рх
,^oV^-
1крх^,
Сравнивая результаты, получим
V^
=
2F^,
что и требовалось
доказать.
3.8.
Найти объем тела, образованного вращением фигуры,
ограниченной
линиями:
у - cos х и ^ = -1 вокруг прямой у
— —\
при
—л:
<х<—;г .
Решение. Тело, образованное вращением фигуры, ограни-
ченной заданными линиями, показано на
рис.
12.26.
Рис. 12.26
Поскольку кривая вращается вокруг прямой
j;
= -l, то
целесообразно перейти к новой системе координат

634
Гпава
12
X - х\ у - у
л-Х.
Тогда объем тела вращения равен
V^п\
(УУС1Х'
= ЯГ {y
+
\)dx
=
7ir (cosx
+
\fdx =
J-n J-л J-K
-i:(l
+
cos
2JC
+
2 cos
л:
\dx =
K—x
2
••Зя'
3.9.
Найти объем тела, образованного вращением вокруг
полярной оси: а) кардиоиды р
=
a(l-'COS(p);
б) лемнискаты
р^
=a^cos2^.
Решение, а) Очевидно, что
(р
изменяется от О до ;г (рис. 3.61).
Отсюда по формуле (6) имеем
2 с^ -1 -7 2 т f^ -1
V
=
—K\
а (l-cos(pysin(pd(p
= —Ka
\ (l-cos(p)d(l-cos(p) =
^ 3/1 ч4Г о 3
= —ка {l-cos(p)\
=-7Га
F
8
1о
3'
б) Так как лемниската симметрична относительно начала
координат
(рис.
3.62), то половина объема по формуле (6) равна
2
- 3 . ./
2 3
I 2 сУ - 2 сУ -
-V =-яу "^a\cos2(py
sm(pd(p =
-na^у
^{2cos^
(p-iy
smcpdcp.
^ 1 . ,
cos tdt
Сделаем замену:
cos (p
= ^ —, sm
(pd(p
= -7=—7-; при
л/2 sin
^
>y2sin^r
Ф
= 0,
^
=—;приф =
—, ^
=
—,
тогда
4 4 2
F =
3
r%
cos"^
tdt 4 3
ка , — = —т=ка
Зл/2 WA sin'/
3V2'
\
2+sin^/
\dt
=
J
ЗлЯ
па
-cigt-2t+-
2
/
1 .
t sin2^
2
ЛЛ
^
-—ка'
6
2

ПРИПОЖЕНИЕ ОПРЕЛЕПЕННОГО ИНТЕГРАПА
635
ЗЛО.
Найти объем тела, образованного вращением: а) од-
ной ветви циклоиды x
=
a{t- sin
Г),
у
=
а(\-
cos
t) вокруг оси
Ох\ б) фигуры, ограниченной кривой х =
3/^,
y
=
2\nt и осями
координат, вокруг координатных осей; в) астроиды х
= а
cos /,
у
= а
sin^
t вокруг прямой х
=
а.
Решение, а) Одна ветвь циклоиды получается при измене-
нии
^
от
О
до 2л:, а
X
от
О
до 27га (рис. 3.67). Следовательно,
искомый объем равен
К = л:| y^dx.
Используя параметрические уравнения циклоиды, получим
V
=
ка'
J'""
(1
-
cos
Г)'
dt
=
па"
j'''
^ 3
l-3cosr
+ -(l-hcos20-
V
-(1-sin^Ocos/ т-%а'
/5 3 1^
—^-4sin
1Л—sin2^H—sin^/
2 4 3
2л:
:57rV.
б) Фигура, ограниченная заданной кривой и осями коорди-
нат, показана на рис. 12.27, где
^е]0,1].
Объем тела вращения
вокруг оси Ох находим по формуле
V = KJ y^dx или V =
24KJ
tln^tdt.
Рис. 12.27

636 Гпава 12
При / = 0 подынтегральная функция терпит
разрыв.
Интег-
рируя несобственный интеграл дважды по частям: \n^t
=
u,
1 t^
2 ~In
tdt = du; tdt =
dv^
v = —, получим
/
К = 24л:ит
^^0
\
\p jfi
f tin
tdt
:24л:
/3->o 2
J8^
+ lim
— \nt+—
, 2 4
••2Ал
f 1 ^
- hm-t-——+hm-^—In б +-
^->o 4 /3^0 2 4
J8^
= 24л:
lim—-^
+ —
= 6л:.
^-»o 1
Объем тела вращения вокруг оси Оу находим по формуле
(3).
При у =
-оо,
/ = 0; при 7 = 0, / =
1,
отсюда
^ ^dt 9
V = K\ X dy =
97r\
r — = -7tt
J-^ -^ Jo ^ 4
9
= —7t.
4
в) Поскольку астроида симметрична относительно оси Ох,
то
достаточно найти половину объема тела вращения
(рис.
12.28).
Так как астроида вращается вокруг прямой х = а, то перенесем
начало координат
в
точку
(afi),
тогда
в
новой системе координат
х'
=
х-а, у'
=
у формула для вычисления объема примет вид
^V
=n[{xyd/
=
nllix-aydy.
Рассматривая только объем тела, получающийся от враще-
ния вокруг прямой х
=
а фигуры, ограниченной верхними вет-
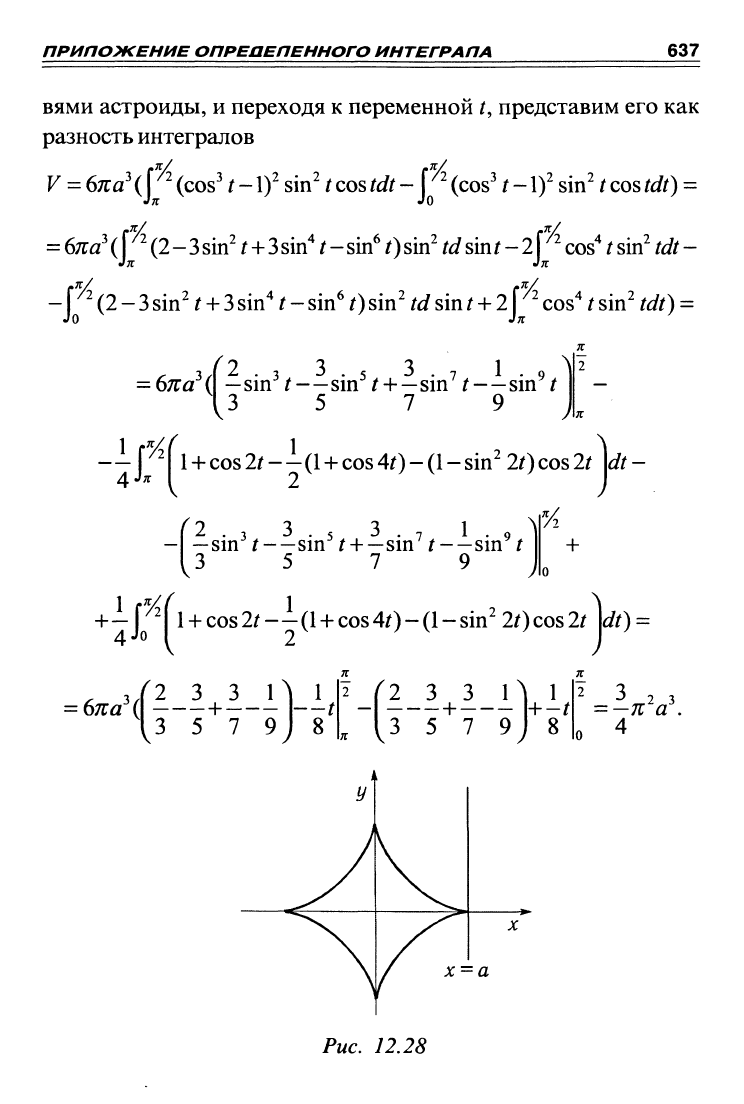
ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА
637
ВЯМИ
астроиды, и переходя к переменной /, представим его как
разность интегралов
V = вка' (1 (cos^ t
-1)^
sin^
t cos tdt
-y^
(cos^
t
-1)^
sin^
t cos tdt)
=
=
6^^^(r^(2-3sin^/
+ 3sin^^-sin^0sin^^^sin/-2K^cos'^/sin^^fi?/--
-J (2-3
sin^
t
+ 3
sin''
t - sin^ 0
sin^
td sin
t +
l\
cos"*
t
sin^
tdt) =
= 6паЦ
2.
. -i J. 5 J. 7 l.g
— sin ? sin t-i sin / sin /
3 5 7 9
— f'^ l + cos2^—(H-cos40-(l-sin^20cos2r
\dt-
(2 . , 3.5 3.7 1.9
- —sm /—sin^
+—sin
/ — sin r
3 5 7 9
Уг
+
~A
1
2 ^
+ cos 2t—(1 +
cos
4t) -
(1
- sin 2/)
cos 2t
3.1 2 3 3 П
= 6жа\\ + —
3 5 7 9
1
—t
8
.35798
\dt)
=
2 3
= -n'a\
Рис. 12.28

638 Гпава
12
12.4. Длина дуги кривой
1°.
Если плоская кривая отнесена
к
прямоугольной систе-
ме координат и задана уравнением
у = /(х) или х = F{y), или
параметрически
jc
=
(p{t),
j;
=i//(/),
то
дифференциал ^f/длины
ее дуги (рис. 12.29) определяется, соответственно,
по
форму-
лам
rf/
=
^1
+
{yf
dx =
^l
+
(xf
dy
=
yjx"
+ y^
dt.
(1)
Интегрируя дифференциал дуги
в
заданных пределах,
на-
ходим длину дуги
b
b d )3
L^\dl
=
\4^
+ {yydx
=
\4\-^{xfdy--\yjx'+y''dt.
(2)
а
а с а
2°.
Если плоская кривая отнесена
к
полярной системе коор-
динат
и
задана уравнением
р =
p{q>)
(рис.
12.30),
то
дифферен-
циал дуги равен
dl - yjр^
+ {p'Yd(p,
а
длина дуги определяется
по формуле
^
L =
\4p'Hpydcp, (3)
Рис.
12.30

ПРИПОЖЕНИЕ ОПРЕПЕПЕННОГО ИНТЕГРАПА
639
3°.
Длина дуги пространственной кривой, заданой парамет-
рически уравнениями х
=
х(/), у
=
y{t), z
=
z{t) при изменении
t
от сс
до р, определяется по формуле
L
=
j^x^+y^+z^dt.
(4)
а
4.1.
Найти длину дуги: а) кривой
>^
= lncosx от
jc
= 0 ДО
я
^ = т-; б) астроиды х^'^
+у^^^
-о^'^\
в) кривой
j;^
=9-х между
точками пересечения
ее с
осью Оу\ г) полукубической параболы
З;^
= х\ заключенной внутри окружности
х^^
+у^ =6х.
Решение, а) Применяя формулу
(1),
имеем
ГА
Уг
L=y'Jl+[ilncosxyfdx= f/\ l+iliLljx= f'
Jo ^ Jo V rn^^ V Jo
'Yi dx
cos X
cosx
= lim In
^-1
tg
X
ж
—h—
2 4
= lim
In
tg
^-f
P 7t
+ — =oo.
2 4
6) Поскольку астроида симметрична относительно коорди-
натных осей (рис. 12.28), то достаточно найти длину одной ее
ветви. Дифференцируя уравнение астроиды, имеем у=-{у1х)^'^.
Длина одной четверти астроиды находится
по
формуле
(2) и
равна
и=\14^ну1хг<к=\1^
;с"'+/'=
2/3
dx =
Jo v^^^ 9
X
3
-а.
Отсюда длина всей астроиды L
=
6a-
в) Кривая представляет параболу симметричную относи-
тельно оси Ох (рис. 12.31).
