Чейз, Ричард, Б., Эквилайн, Николас, Дж., Якобе, Роберт, Ф. Производственный и операционный менеджмент

Подождите немного. Документ загружается.

Глава

13.

Прогнозирование

411

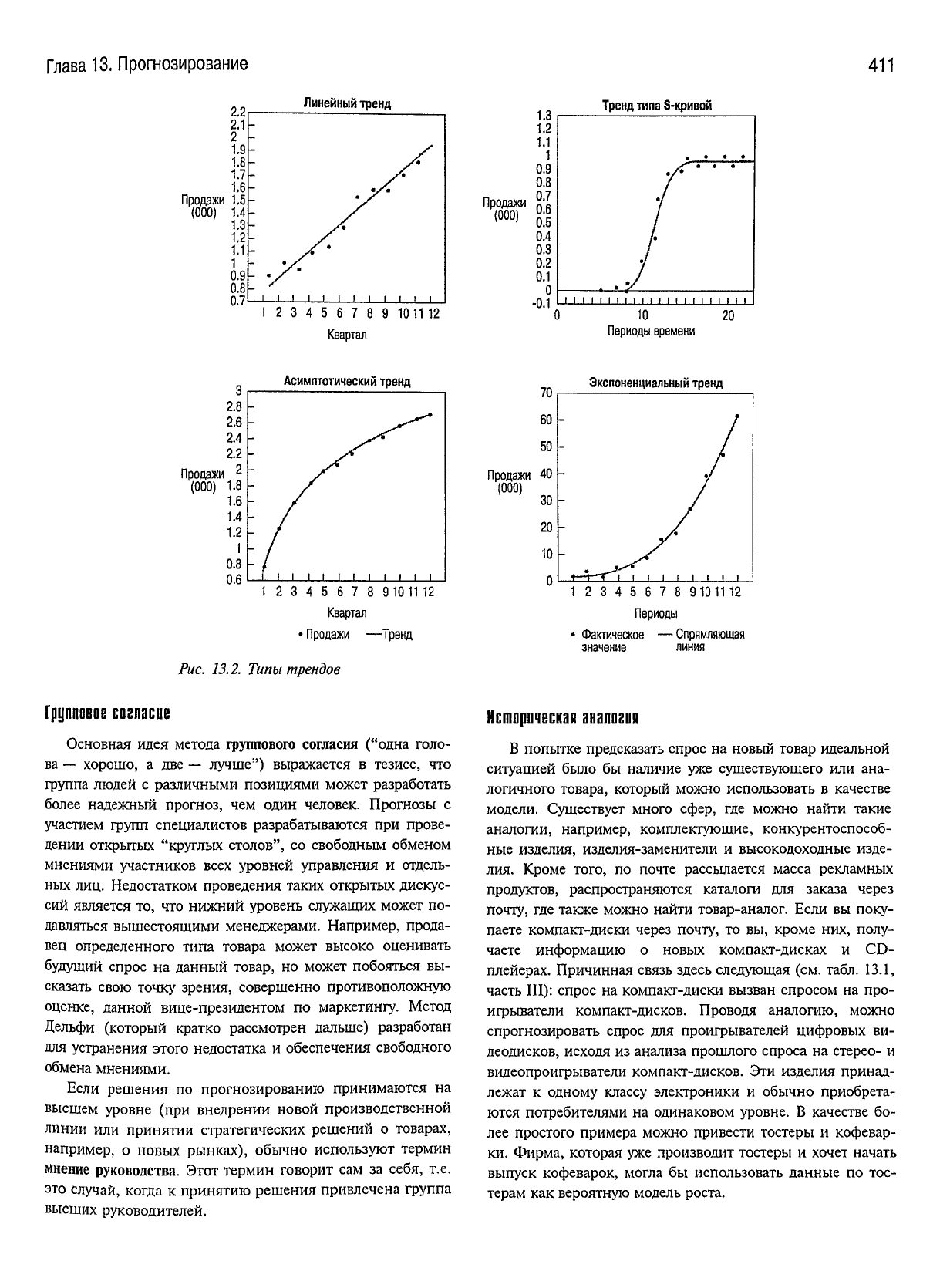
Линейный тренд

Тренд типа S-кривой

1011 12

Квартал

Асимптотический тренд

Экспоненциальный тренд

4 5 6 7 8

91011 12

Квартал

Продажи —Тренд

Рис. 13.2. Типы

трендов

Групповое согласие

Основная

идея метода

группового

согласия

("одна голо-

ва

—

хорошо,

а две —

лучше")

выражается

тезисе,

что

группа людей

различными позициями может разработать

более надежный прогноз,

чем

один человек. Прогнозы

участием групп специалистов разрабатываются

при

прове-

дении открытых

"круглых

столов",

со

свободным обменом

мнениями

участников

всех

уровней управления

отдель-

ных лиц. Недостатком проведения таких открытых дискус-

сий

является

то, что

нижний уровень служащих может

по-

давляться вышестоящими менеджерами. Например, прода-

вец определенного типа товара может высоко оценивать

будущий спрос

на

данный товар,

но

может побояться

вы-

сказать свою точку зрения, совершенно противоположную

оценке,

данной вице-президентом

по

маркетингу. Метод

Дельфи (который кратко рассмотрен дальше) разработан

для устранения этого недостатка

обеспечения свободного

обмена мнениями.

Если решения

по

прогнозированию принимаются

на

высшем уровне

(при

внедрении новой производственной

линии

или

принятии стратегических решений

товарах,

например,

новых рынках), обычно используют термин

Мнение

руководства.

Этот термин говорит

сам за

себя,

т.е.

это случай, когда

принятию решения привлечена группа

высших руководителей.

Продажи

(000)

2 3 4 5 6 7 8

9101112

Периоды

•

Фактическое —Спрямляющая

значение линия

Историческая аналогия

В попытке предсказать спрос на новый товар идеальной

ситуацией было бы наличие уже

существующего

или ана-

логичного товара, который можно использовать в качестве

модели.

Существует

много сфер, где можно найти такие

аналогии,

например, комплектующие, конкурентоспособ-

ные

изделия, изделия-заменители и высокодоходные изде-

лия.

Кроме того, по почте рассылается масса рекламных

продуктов, распространяются каталоги для заказа через

почту,

где также можно найти товар-аналог. Если вы поку-

паете компакт-диски через

почту,

то вы, кроме них, полу-

чаете

информацию о новых компакт-дисках и CD-

плейерах. Причинная связь здесь следующая (см. табл. 13.1,

часть

III):

спрос на компакт-диски вызван спросом на про-

игрыватели компакт-дисков. Проводя аналогию, можно

спрогнозировать спрос для проигрывателей цифровых ви-

деодисков, исходя из анализа прошлого спроса на стерео- и

видеопроигрыватели компакт-дисков. Эти изделия принад-

лежат

к одному классу электроники и обычно приобрета-

ются потребителями на одинаковом уровне. В качестве бо-

лее простого примера можно привести тостеры и кофевар-

ки.

Фирма, которая уже производит тостеры и

хочет

начать

выпуск кофеварок, могла бы использовать данные по тос-

терам как вероятную модель роста.

412

Часть

IV.

Управление

снабжением

Метод

Дельфи

Как

уже упоминалось в связи с методом группового

согласия, заявление или мнение вышестоящего чиновни-

ка,

вероятно,

будет

весить больше, чем мнение его под-

чиненных. При этом часто подчиненные боятся высказать

свои настоящие соображения, опасаясь гнева руководства.

Для устранения этого в методе Дельфи обеспечивается

конфиденциальность

участвующих

в исследовании лиц.

Каждый участник имеет одинаковый вес. Председательст-

вующий готовит анкету (вопросник) и раздает ее участни-

кам.

Их ответы подытоживаются и возвращаются всей

группе вместе с новым перечнем вопросов.

Метод Дельфи разработан в 50-х

годах

компанией

Rand.

Ниже приведены основные стадии осуществления

этого метода.

1. Выберите экспертов. Это должны быть специалисты-

профессионалы, представляющие различные области.

2. С помощью вопросника (или электронной почты) полу-

чите прогнозы (замечания или уточнения прогнозов)

ото

всех

участников.

3. Подведите итоги и раздайте полученные выводы

участ-

никам

с соответствующими новыми вопросами.

4. Снова подведите итоги, совершенствуя прогнозы и ус-

ловия,

опять разработайте новые вопросы.

5. Повторите в

случае

необходимости п. 4. Ознакомьте с

окончательными результатами

всех

участников.

Обычно с помощью метода Дельфи можно достичь

удовлетворительных

результатов

уже за три раунда. Про-

должительность составления прогноза зависит от числа

участников, объема работы, выполняемой при разработке

прогноза, и быстроты ответов участников.

Анализ временных рядов

Модели временных рядов прогнозируют

будущее,

ис-

ходя

из прошлых данных. Например, данные о продажах,

собранные за последние шесть недель, можно использо-

вать для прогнозирования продаж на еще не наступив-

шую

седьмую

неделю. Поквартальные данные продаж,

собранные за несколько последних лет, можно использо-

вать для прогнозирования продаж

будущих

кварталов. Не-

смотря на то, что оба примера содержат данные о преды-

дущих

продажах, для прогнозирования, вероятно,

будут

использоваться различные модели временных рядов.

В табл. 13.2 показаны модели временных рядов и не-

которые их характеристики.

Обратите внимание, что в табл. 13.2 представлены ме-

тоды от очень простых до очень сложных. В этой таблице

не

указан метод простого скользящего среднего, характе-

ристики

которого аналогичны

методу

простого

экспонен-

циального сглаживания. Отметим, что определение взве-

шенного скользящего среднего может быть весьма запу-

танным,

особенно если прогнозист включает в прогноз

сезонные или

другие

циклические факторы, влияющие на

прогноз.

Его характеристики находятся

между

характери-

стиками методов экспоненциального сглаживания

Холта

экспоненциального сглаживания Винтера. Здесь под-

робно не рассматриваются модели

Холта

и Винтера, но

если у читателя возникнет желание применить к исход-

ным

данным такие разновидности экспоненциального

сглаживания, то он сможет найти их в литературе.

Признавая,

что термины

краткосрочный,

среднесрочный

долгосрочный

зависят от контекста, в котором они ис-

пользуются, обратим внимание, что в бизнес-

прогнозировании термин

краткосрочный

обычно означает

период времени до

трех

месяцев;

среднесрочный

— от

трех

месяцев до

двух

лет;

долгосрочный

— свыше

двух

лет. Во-

обще говоря, модели краткосрочного прогноза усредняют

случайные изменения и

регулируют

краткосрочные коле-

бания

(типа реакций потребителей на новое изделие).

Среднесрочные прогнозы полезны при наличии сезонных

колебаний,

а модели долгосрочных прогнозов устанавли-

вают

общие тренды и особенно полезны в определении

границ прогнозов.

При

выборе модели прогнозирования фирме

следует

руководствоваться таким данными.

1. Временной горизонт прогнозирования.

2. Исходные данные.

3. Требуемая точность.

4. Бюджет, выделенный для разработки прогноза.

5. Уровень квалификации персонала.

При

выборе модели прогнозирования

существуют

другие

проблемы, например степень гибкости фирмы.

(Чем

лучше

фирма способна реагировать на изменения,

тем менее точным может быть прогноз.) Еще одна важная

проблема — это последствия плохих прогнозов. Если ре-

шение о крупных инвестициях должно базироваться на

прогнозе, то прогноз должен быть очень хорошим.

Простое

скользящее

среднее

Если спрос на изделие стабильный (не растет и не па-

дает), не носит сезонного характера и имеет лишь слу-

чайные флуктуации, для прогноза можно использовать

метод скользящего среднего. Учитывая, что

скользящие

средние

центрированы и усреднены за небольшой интер-

вал времени, этот метод наиболее

удобен

для непосредст-

венного предсказания последующего периода времени.

Например,

центрированное пятимесячное среднее января,

февраля, марта, апреля и мая приходится на март. При

этом нужны данные

всех

пяти месяцев. Если нашей це-

лью является прогноз на июнь, то мы должны каким-то

образом при отсутствии фактических данных за

будущие

июнь,

июль и

август

определить наше скользящее среднее

с марта по июнь. Таким образом, появляется временной

разрыв

между

месяцем центрирования и прогнозируемым

месяцем, что снижает точность прогноза, если пользо-

Глава

13.

Прогнозирование

413

ваться только имеющимися данными, чем и приходится

чаше всего довольствоваться на практике. Если мы хотим

сделать прогноз на июнь, используя пятимесячное сколь-

зящее среднее,

берут

средние значения за январь, фев-

раль, март, апрель и май. После июня для прогноза на

июль

следует

брать средние значения за февраль, март,

апрель, май и июнь и т.д. Этот метод иллюстрируется ре-

зультатами прогнозирования, приведенными в табл. 13.3

на рис. 13.3.

Важно выбрать наилучший интервал усреднения для про-

стого скользящего среднего, он зависит от разрешения сле-

дующего

противоречия: чем длиннее интервал усреднения,

тем лучше сглаживаются флуктуации (которые иногда

даже

желательны), но если в исходных данных наблюдается тренд

роста или спада, то усиливается эффект запаздывания тренда

(лаговый

эффект).

Поэтому, несмотря на то, что короткий

интервал усреднения

дает

большие разбросы, его использо-

вание лучше отслеживает тренд. И наоборот, более продол-

жительный интервал усреднения

дает

сглаженный результат,

но

приводит к лаговому эффекту.

Таблица

13.2.

Характеристики методов прогнозирования,

основанных

на анализе временных

рядов

Метод

прогнозирования

Количество

стати-

стических

данных

Модель данных

Горизонт

прогноза

Время,

затрачивав-

Подготовка

мое на

подготовку

персонала

прогноза

Простое экспонен-

циальное сглажи-

вание

Экспоненциальное

сглаживание

Холта

(Holt)

Экспоненциальное

сглаживание Вин-

тера

(Winter)

Регрессионные

трендовые модели

Причинные регрес-

сионные модели

Декомпозиция

временных рядов

Метод Дженкинса

От

до 10 наблю-

дений

для

установ-

ления весовых ко-

эффициентов

От 10 до

наблю-

дений

для

установ-

ления весовых ко-

эффициентов

По меньшей мере

4-5 наблюдений

за

сезон

От

до

20;

для

сезонного

по

меньшей мере

5 за

сезон

10 наблюдений

на

независимую пере-

менную

Достаточно

двух

экстремальных

значений

50 или больше

наблюдений

Данные должны

быть

стационарны-

ми

Тренд, без

сезон-

ных колебаний

Тренд и сезонные

колебания

Тренд и сезонные

колебания

Может обрабаты-

вать

сложные мо-

дели

Обрабатывает

цик-

лические

сезон-

ные модели; может

определять экс-

тремальные точки

Должны

быть

ста-

ционарными

или

приведенными

стационарным

Краткосрочный

Малое

От краткосрочного Малое

до среднесрочного

От краткосрочного Малое

до среднесрочного

От краткосрочного Малое

до среднесрочного

Краткосрочный,

среднесрочный

долгосрочный

От краткосрочного

до среднесрочного

Краткосрочный,

среднесрочный

долгосрочный

Имеет

длительный

период

разработки

и малое время

внедрения

От малого до сред-

него

Продолжительное

Особой подготов-

ки

не требуется

Достаточно общей

подготовки

Средний уровень

подготовки

Средний уровень

подготовки

Высокий уровень

подготовки

Не требует осо-

бой подготовки

Высокий уровень

подготовки

Источник.

Holton

Wilson

and Deborah Allison-Koerber, "Combining Subjective and Objective Forecasts Improves Results", Journal of

Busi-

ness

Forecasting,

Fall

1992, p.

Таблица

13.3.

Текущий спрос

прогноз методом простого скользящего среднего при трех-

девятинедельном интервале усреднения

Неделя

Спрос

800

1400

1000

1500

1300

Трехнедельное

усреднение

1067

1300

1333

Девягинедельное

усреднение

Неделя

Спрос

1700

1800

2200

1900

2400

Трехнедельное

усреднение

2200

2000

1833

1900

1967

2167

Девягинедельное

усреднение

1811

1800

1811

1911

1933

2011

414

Часть IV. Управление снабжением

Окончание табл.

13.3

Неделя

Спрос

1800

1700

1300

1700

1500

2300

2800

2000

Трехнедельное

усреднение

1433

1533

1600

1567

1633

1833

2033

2,800

2,400

2,000

1,600

1,200

800

400

Девятинедельное

усреднение

1367

1467

1500

1556

1644

1733

_ Фактические

Хзначения

у>

i i i

Неделя

чЛ

Спрос

2600

2000

2500

2600

2200

2500

2400

2100

Трехнедельное

усреднение

2233

2467

2333

2367

2433

2333

2300

2367

/среднение за 3

недели

....

-Усреднение за 9

недель

Девятинедельное

усреднение

2111

2144

2111

2167

2267

2311

2378

20 24 28 32

Рис. 13.3.

Прогноз

методом

простого

скользящего

среднего

при

трех-

и де-

вятинедельном

интервале

усреднения

по

сравнению

текущим

спросом

Формула для вычисления простого скользящего сред-

него:

р _ Д-l

Д-2

"*"

Д-3

"*"

•••

Д-я

•

/1О ])

где F, — прогноз на будущий период;

п — интервал (число периодов) усреднения;

Д.,

— фактическое значение в прошлом периоде;

Д_

Д.„ — фактические значения два периода назад,

три периода назад и так далее до п периодов назад.

Графики

на рис. 13.3, построенные по данным

табл. 13.3, показывают влияние интервала усреднения на

значение

скользящего среднего. Мы видим, что тренд

роста выравнивается примерно к 23-й неделе. Трехне-

дельное усреднение лучше отражает фактические измене-

ния

спроса, чем девятинедельное, хотя последнее более

сглаженное.

Одним из недостатков метода простого скользящего

среднего является необходимость статистического

учета

хранения

всех прошлых данных. При ограниченной но-

менклатуре товаров и интервале усреднения от

трех

до

шести периодов это не очень существенно. Но при вы-

числении

скользящих средних, например, при 60-

периодном усреднении для каждого из 20 тысяч наимено-

ваний

материальных запасов потребуется значительное

количество данных.

Взвешенное

скользящее

среднее

При

определении простого скользящего среднего каж-

дому элементу базы данных присваивается равный вес, а

при

расчете взвешенного скользящего среднего им может

присваиваться любой произвольный вес, при условии, что

сумма всех весов равна 1. Например, магазин может обна-

ружить, что при четырехмесячном интервале усреднения

наилучший прогноз оказывается при использовании веса,

равного 40% для продаж истекшего месяца; веса, равного

30% для месяца, предшествующего истекшему месяцу,

20% — третьему от истекшего месяцу и 10% — четвертому

месяцу. Если текущий уровень продаж составлял:

Месяц

100

Месяц

105

Месяц

то прогноз на пятый месяц

будет

следующим:

= (0,40 х 95) + (0,30 х 105) + (0,20 х 90) +

(0,10 х 100) = 97,5.

Ниже

приведена формула для вычисления взвешен-

ного скользящего среднего:

F, = w,4_,

A,_

...w

A,.

;

(

)

где w, — значение веса, присвоенное истекшему периоду

U - 1);

Глава

13. Прогнозирование

415

—

значение веса, присвоенное периоду

—

2);

—

значение веса, присвоенное периоду

—

«);

—

общее число периодов

прогнозе.

Схема присвоения веса может быть любой, например,

некоторые периоды можно игнорировать

(их вес

принять

равным

нулю), более старые периоды

могут

иметь боль-

ший

вес по

сравнению

последними,

но

обязательно

сумма всех весов должна быть равна единице:

Предположим,

что в

нашем примере продажи

в 5-м

месяце составили ПО единиц. Тогда прогноз

на 6-й

месяц

будет

следующим:

= (0,40

х 110) +

(0,30

х 95) +

(0,20

х 105) +

(0,10x90)

102,5.

Выбор

весовых коэффициентов.

Опыт, метод проб

ошибок

являются самым простыми способами выбора

ве-

са.

Как

правило, близкое прошлое служит наиболее

важ-

ным

индикатором

будущего,

значит, этому периоду

времени присваивают более высокий

вес.

Например,

до-

ходы

за

прошлый месяц или производственные мощности

завода лучше оценивать

по

текущему месяцу,

а не

брать

данные трехмесячной давности.

Однако,

если данные имеют сезонные колебания,

это

следует

учитывать

при

установлении весовых

коэффици-

ентов.

Объему продаж купальных костюмов

июле

про-

шлого года

следует

присваивать более высокий

вес, чем

продажам декабря

(в

северном полушарии).

Преимущество метода взвешенного скользящего сред-

него перед простым заключается

возможности влияния

на

прогноз, изменяя результаты прошлых периодов.

Од-

нако

использование этого метода дорого

менее удобно,

чем использование метода экспоненциального сглажива-

ния,

рассматриваемого ниже.

Экспоненциальное сглаживание

Главным недостатком рассмотренных методов прогно-

зирования

(методы простого

взвешенного скользящего

среднего) является необходимость использования боль-

шого количества прошлых данных.

(Это

относится

и к

регрессионному анализу, который

будет

рассмотрен

поз-

же.)

рассмотренных методах новые блоки данных

сум-

мируются

предыдущими, данные, относящиеся

само-

му раннему периоду, исключаются

и,

исходя

из

этого

строится прогноз.

Во

многих случаях

(а,

может быть,

даже

подавляющем большинстве) самые последние данные

наиболее характерны

для

будущего

по

сравнению

более

ранними

данными. Если считать,

что

значимость данных

уменьшается

течением времени,

то

наиболее подходя-

щим

методом усиления влияния последних периодов

яв-

ляется

экспоненциальное сглаживание.

Метод получил название "экспоненциальное сглажи-

вание"

связи

тем,

что

каждое значение периодов,

ухо-

дящих

прошлое, уменьшают

на

множитель

— а).

На-

пример,

если

а =

0,05,

то

коэффициенты взвешивания

для различных периодов

будут

следующими.

Последний период

а(1-а)°

Данные,

полученные

один период

назад а(1-а)

Данные,

полученные

два периода

а(1-а)

Данные,

полученные

три периода

назада(1-а)

Взвешивание

при

а=0,05

0,0500

0,0475

0,0451

0,0429

Экспоненциальное

сглаживание чаще всего использу-

ется

для

прогнозирования. Фактически, этот метод явля-

ется составной частью всех компьютеризированных

про-

грамм прогнозирования

широко используется при зака-

зе запасов

фирмах розничной торговли, оптовых

компаниях

сервисных агентствах.

Метод экспоненциального сглаживания получил

ши-

рокое

распространение

по

таким шести причинам.

1. Экспоненциальные модели на удивление точны.

2. Составление экспоненциальной модели относительно

несложное.

3. Пользователь может понять, как работает модель.

4. Использование модели

требует

немногих вычислений.

5. Требования

памяти компьютера невысоки из-за огра-

ниченного

объема необходимых статистических данных.

6. Несложно выполнить тесты на точность работы модели.

Для прогнозирования

будущего

методом экспоненци-

ального сглаживания необходимы только

три

вида

дан-

ных: данные последнего прогноза, текущий спрос

и кон-

станта

сглаживания а. Эта

константа определяет уровень

сглаживания

скорость реакции

на

разницу

между

про-

гнозами

текущими событиями. Выбор значения

кон-

станты зависит

как от

природы продукта,

так и от

опыта

менеджера

и его

способности быстро реагировать.

На-

пример,

если фирма производит стандартное изделие

относительно стабильным спросом, быстрота реагирова-

ния

на

различия

между

текущим

прогнозируемым спро-

сом нужна невысокая,

от 5 до 10%.

Однако, если фирма

наращивает выпуск, желательно иметь более высокую

скорость реагирования, возможно

от 15 до 30%,

чтобы

придать большую значимость текущему росту.

Чем

выше

темп роста,

тем

выше должна быть скорость реагирова-

ния.

Иногда пользователи простого скользящего среднего

переходят

методу экспоненциального сглаживания,

но

предпочитают придерживаться

при

прогнозировании

тех

же приемов,

что и в

методе простого скользящего сред-

него.

этом

случае

константу сглаживания приблизи-

тельно определяют

по

формуле

•

где я —

число периодов усреднения.

Уравнение

для

однократного экспоненциального сгла-

живания

имеет такой

вид:

-F,

(13.3)

416

Часть IV. Управление снабжением

где

р, _

экспоненциально сглаженный прогноз на период

—

экспоненциально сглаженный прогноз, сделанный

для предшествующего периода;

Д_,

—

фактический спрос

предшествующем периоде;

—

константа сглаживания.

Это уравнение показывает,

что

новый прогноз равен

прогнозу прошлого периода, плюс поправка (разность меж-

ду предыдущим прогнозом

фактическим результатом)

Чтобы продемонстрировать действие метода, примем,

что долгосрочный месячный спрос

на

изучаемый товар

относительно стабилен

поэтому можно принять

кон-

станту сглаживания

а =

0,05. Если экспоненциальный

метод прогнозирования используют постоянно,

то

суще-

ствует

прогноз

для

предшествующего месяца

. Допустим,

что прогноз спроса

на

предшествующий месяц составляет

/)_,

1050

единиц. Если фактический спрос составил

1000 единиц,

а не 1050, то

прогноз спроса

на

месяц

будет

таким:

F,_,

+а(Д_,

- F

) = 1050 +

0,05(1000

1050)

1047,5

единиц.

Поскольку коэффициент сглаживания

мал,

реакция

нового прогноза

на

ошибку

в 50

единиц выражается

снижении

значения прогнозируемого

на

ме-

сяц

спроса только

на 2,5

единицы.

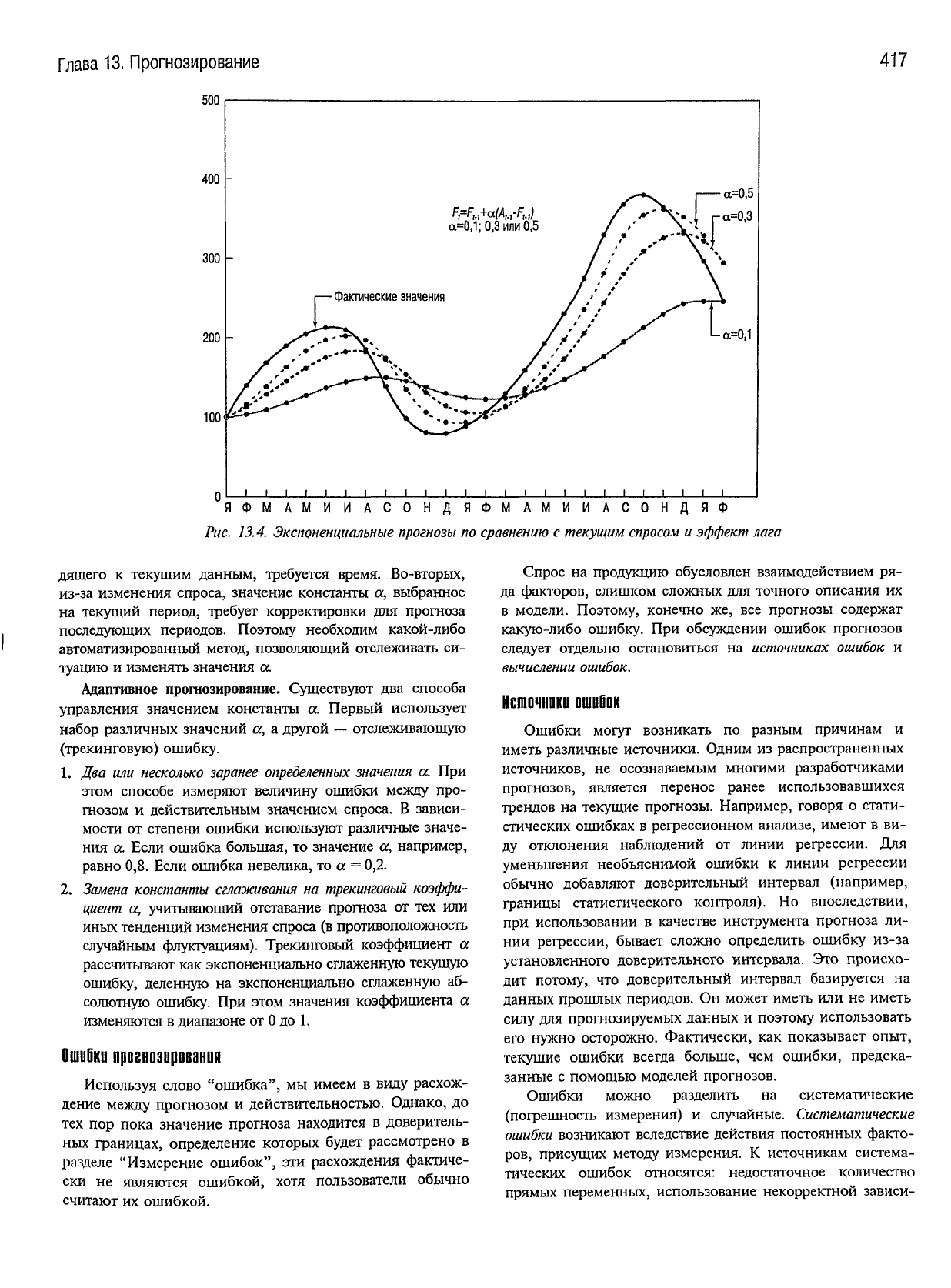
Недостатком однократного экспоненциального сгла-

живания

является лаговый эффект.

На

рис.

13.4

представ-

лены текущие данные

виде сглаженной (плавной)

кри-

вой,

чтобы показать эффекты запаздывания экспоненци-

альных прогнозов. Прогноз запаздывает

периоды роста

или

падения спроса

превышает фактические значения

при

его

уменьшении. Обратите внимание:

чем

выше

зна-

чение

а, тем

точнее прогноз,

тем

ближе

он к

реальным

событиям.

Для

большего соответствия реальному спросу

можно ввести трендовый фактор. Кроме того, можно

из-

менять значение

а. В

таких

случаях

говорят

об

адаптив-

ном

прогнозировании.

Трендовые эффекты

адаптивное

прогнозирование более подробно рассмотрены

следую-

щих

разделах.

Трендовые эффекты при экспоненциальном сглаживании.

Следует

помнить,

что

восходящий

или

нисходящий тренд

данных, собранных

за

последовательные периоды

вре-

мени,

приводит

отставанию экспоненциального прогно-

за

от

фактической ситуации. Экспоненциально сглажен-

ные прогнозы можно откорректировать введением тренда.

Для этого необходимы

две

константы сглаживания.

По-

мимо константы сглаживания

а, в

уравнении тренда

ис-

пользуют

константу сглаживания тренда 8,

которая умень-

Некоторые

авторы предпочитают называть

сглаженным

средним

значением.

Когда метод экспоненциального сглаживания применяют

впервые,

начальный прогноз или стартовое значение можно

по-

лучить

помощью простой оценки

или

усреднения значений

предыдущих периодов, например, взяв среднее значение первых

двух

или трех периодов.

шает влияние ошибки,

т.е.

разности

между

действитель-

ным

значением

прогнозируемым. Если

оба

коэффици-

ента сглаживания

не

включены

уравнение, вероятность

ошибки

возрастает.

В первом периоде возникает проблема определения

начального значения тренда, которое

следует

выбрать ли-

бо

из

предположений, основанных

на

фактах, либо

из

ориентировочного расчета

по

данным

прошлых перио-

дах для аналогичных товаров.

Ниже

приведены уравнения

для

вычисления прогноза

с использованием тренда

(FIT):

FIT

F,+T,;

(13.4)

FIT,

a(4_,

FIT,.,);

(13.5)

T,=T,_

+a8(A,_,-FIT

);

(13.6)

где

F, —

экспоненциально сглаженный прогноз на период

Т, —

экспоненциально сглаженный тренд

на

период

FIT,

—

прогноз, включающий тренд

периоде

FIT,_i

—

прогноз, включающий тренд предыдущего периода;

Д_,

—

фактический спрос

предыдущем периоде;

—

константа сглаживания прогноза;

—

константа сглаживания тренда.

Пример

13.1.

Прогноз

трендовым

регулированием

Примем,

что

исходный

прогноз

/=•_,

100

единицам, тренд

=10,

сс=

0,20 и

0,30. Рассчитайте

прогноз

на следующий

период,

при условии,

что

значение фактического

спроса

оказа-

лось

равно 115,

его

прогнозное

значение

—

100.

Решение

Сложив значения

исходного

прогноза

тренда,

получим:

FIT,_,

F,_,

T,_,=

100

110.

Значение

фактического

спроса

Д.,

равно 115, поэтому:

FIT,,,

+a(A

-FlT,_,)

110 + 0,2(115

110)

111,0;

Т,

Т,_,+сс8(А,^

-FIT

)

(0,20)(0,30)(115-110)

= 10,3;

FIT

F, +

=111,0

10,3

121,3.

Если значение фактического

спроса

окажется

120

вместо

121,3,

то

процедуру следует повторить

прогноз

на следующий

период

будет

таким:

121,3

0,2(120

121,3)

121,04;

10,3

(0,2)(0,3)(120-

121,3)

10,22;

FIT

121,04

10,22

131,26.

Выбор

значения константы сглаживания прогноза.

Экспо-

ненциальное сглаживание

требует,

чтобы константа сгла-

живания

находилась

диапазоне

от 0 до 1.

Если реаль-

ный

спрос стабильный (например, спрос

на

электроэнер-

гию

продукты питания),

то для

снижения влияния

краткосрочных

или

случайных колебаний

следует

исполь-

зовать небольшую величину

а.

Если реальный спрос быст-

ро увеличивается или уменьшается,

то

для

учета

изменений

лучше

брать большее значение константы сглаживания

ее

Идеальным было

бы

предугадать

точное значение

ос К со-

жалению, этому мешают

два

обстоятельства. Во-первых,

для определения значения

а,

наилучшим образом подхо-

Глава

13. Прогнозирование

417

500

400

300

100

0=0,1

ЯФМАМИИАСОНДЯФМАМИИАСОНДЯФ

Рис. 13.4.

Экспоненциальные

прогнозы

по

сравнению

текущим

спросом

эффект

лага

дящего

текущим данным,

требуется

время. Во-вторых,

из-за изменения спроса, значение константы

а,

выбранное

на

текущий период,

требует

корректировки

для

прогноза

последующих периодов. Поэтому необходим какой-либо

автоматизированный метод, позволяющий отслеживать

си-

туацию

изменять значения

а.

Адаптивное прогнозирование.

Существуют

два

способа

управления значением константы

а.

Первый использует

набор различных значений

а, а

другой

—

отслеживающую

(трекинговую) ошибку.

Два или

несколько

заранее

определенных

значения

а. При

этом способе измеряют величину ошибки

между

про-

гнозом

действительным значением спроса.

зависи-

мости

от

степени ошибки используют различные значе-

ния

а.

Если ошибка большая,

то

значение

а,

например,

равно 0,8. Если ошибка невелика,

то а = 0,2.

Замена

константы

сглаживания

на

трекинговый

коэффи-

циент

а,

учитывающий отставание прогноза

от тех или

иных тенденций изменения спроса (в противоположность

случайным флуктуациям). Трекинговый коэффициент

рассчитывают как экспоненциально сглаженную

текущую

ошибку, деленную

на

экспоненциально сглаженную

аб-

солютную ошибку. При этом значения коэффициента

изменяются

диапазоне

от 0

до

ОшиОки прогнозирования

Используя слово "ошибка",

мы

имеем

виду

расхож-

дение

между

прогнозом

действительностью. Однако,

до

тех

пор

пока значение прогноза находится

доверитель-

ных границах, определение которых

будет

рассмотрено

разделе "Измерение ошибок",

эти

расхождения фактиче-

ски

не

являются ошибкой,

хотя

пользователи обычно

считают

их

ошибкой.

Спрос

на

продукцию обусловлен взаимодействием

ря-

да факторов, слишком сложных

для

точного описания

их

модели. Поэтому, конечно

же, все

прогнозы содержат

какую-либо ошибку.

При

обсуждении ошибок прогнозов

следует

отдельно остановиться

на

источниках

ошибок

вычислении

ошибок.

Источники ошиОок

Ошибки

могут

возникать

по

разным причинам

иметь различные источники. Одним

из

распространенных

источников,

не

осознаваемым многими разработчиками

прогнозов, является перенос ранее использовавшихся

трендов

на

текущие прогнозы. Например, говоря

стати-

стических ошибках

регрессионном анализе, имеют

в ви-

ду отклонения наблюдений

от

линии регрессии.

Для

уменьшения необъяснимой ошибки

линии регрессии

обычно добавляют доверительный интервал (например,

границы статистического контроля).

Но

впоследствии,

при

использовании

качестве инструмента прогноза

ли-

нии

регрессии, бывает сложно определить ошибку из-за

установленного доверительного интервала.

Это

происхо-

дит потому,

что

доверительный интервал базируется

на

данных прошлых периодов.

Он

может иметь или

не

иметь

силу

для

прогнозируемых данных

поэтому использовать

его нужно осторожно. Фактически,

как

показывает опыт,

текущие ошибки

всегда

больше,

чем

ошибки, предска-

занные

помощью моделей прогнозов.

Ошибки

можно разделить

на

систематические

(погрешность измерения)

случайные.

Систематические

ошибки

возникают вследствие действия постоянных факто-

ров,

присущих

методу

измерения.

источникам система-

тических ошибок относятся: недостаточное количество

прямых переменных, использование некорректной зависи-

418

Часть

IV. Управление снабжением

мости

между

переменными, применение неверной трендо-

вой линии, ошибочный сдвиг сезонного спроса (не в ту

сторону) и наличие необнаруженного тренда во временных

рядах.

К случайным ошибкам можно отнести те, которые

нельзя объяснить используемой моделью прогноза.

Измерение ошибок

Для описания ошибок используют несколько общих

понятий:

стандартная

ошибка,

среднее

квадратов

ошибок

(дисперсия)

среднее

абсолютное

отклонение.

Кроме того,

прогнозировании для

учета

позитивных и негативных

систематических отклонений используют

трекинг.

Стандартная ошибка

будет

обсуждаться

в разделе, по-

священном линейной регрессии. Стандартная ошибка оп-

ределяется корнем квадратным функции, поэтому

удобнее

использовать саму функцию, которая является средним

квадратов ошибок, или дисперсией.

Среднее абсолютное отклонение (Mean

Absolute

Deviation — MAD) раньше часто употреблялось, но со вре-

менем от него стали отказываться в пользу измерения

стандартного отклонения и стандартной ошибки. В по-

следние годы опять вернулись к MAD из-за его простоты и

надежности при оценке трекинга. MAD представляет собой

среднее значение ошибки в прогнозах, которое, как и стан-

дартное отклонение, измеряет разброс некоторого наблю-

даемого процесса от некоторого ожидаемого процесса.

MAD вычисляют как разность

между

действительным

прогнозируемым спросом без

учета

знака, по

следую-

щей формуле:

(13.7)

где / — номер периода;

— текущий спрос данного периода;

F — прогнозируемый спрос данного периода;

п — общее количество периодов;

| — символ модуля (абсолютной величины).

При

нормальном распределении ошибок прогноза

(что, как правило, и наблюдается на практике) среднее

абсолютное отклонение следующим образом взаимосвя-

зано

со стандартным отклонением:

стандартное отклонение

-ё

xMAD,

или

примерно 1,25 MAD.

наоборот: 1 MAD = 0,8 стандартного отклонения.

Стандартное отклонение обычно большая величина.

Если установлено, что MAD набора точек равно 60 едини-

цам,

то стандартное отклонение

будет

равно 75 единицам.

В обычном статистическом анализе, если контрольные

границы были установлены как ±3 стандартных отклоне-

ния

(или ± 3,75 MAD), то 99,7% точек

будут

находиться в

этих границах.

Трекинг является инструментом, индицирующим, на-

сколько точно прогноз

"идет

в ногу" с фактическим

уменьшением или увеличением спроса. В прогнозирова-

нии

трекинг — это отношение суммарной ошибки про-

гноза к

соответствующему

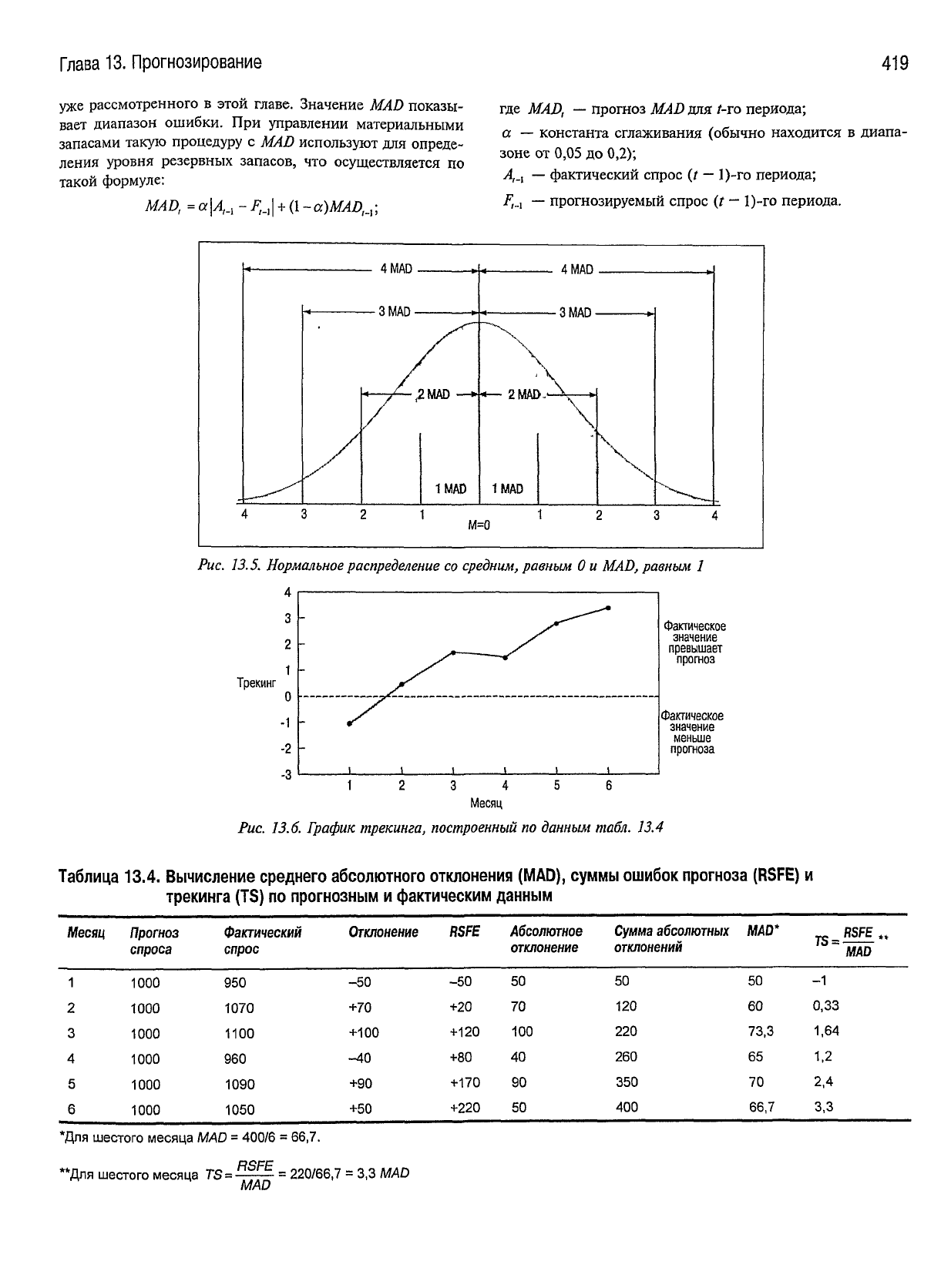
значению MAD. На рис. 13.5

показано

нормальное распределение со средним, равным

нулю

и MAD = 1. Если, например, трекинг равен -2, то

можно сказать, что модель прогноза еще обеспечивает,

получение достаточно точных значений прогноза.

Трекинг (TS) можно вычислить как арифметическую

сумму

отклонений прогнозов, деленную на среднее абсо-

лютное отклонение:

где

RSFE—

алгебраическая сумма ошибок прогноза

(Running Sum of Forecast Errors), учитывающая

знак

ошибки

(отрицательные ошибки компенсируют положи-

тельные и наоборот);

MAD — среднее

всех

абсолютных отклонений

(независимо от того, это положительные или отрицатель-

ные отклонения).

В табл. 13.4 представлена процедура вычисления

MAD и трекинга для шестимесячного периода, где про-

гнозируемый месячный спрос был установлен одинако-

вым и равным 1000. Здесь же показан фактический спрос.

В этом примере среднее абсолютное отклонение со-

ставило 66,7 единиц, а трекинг равен 3,3 MAD.

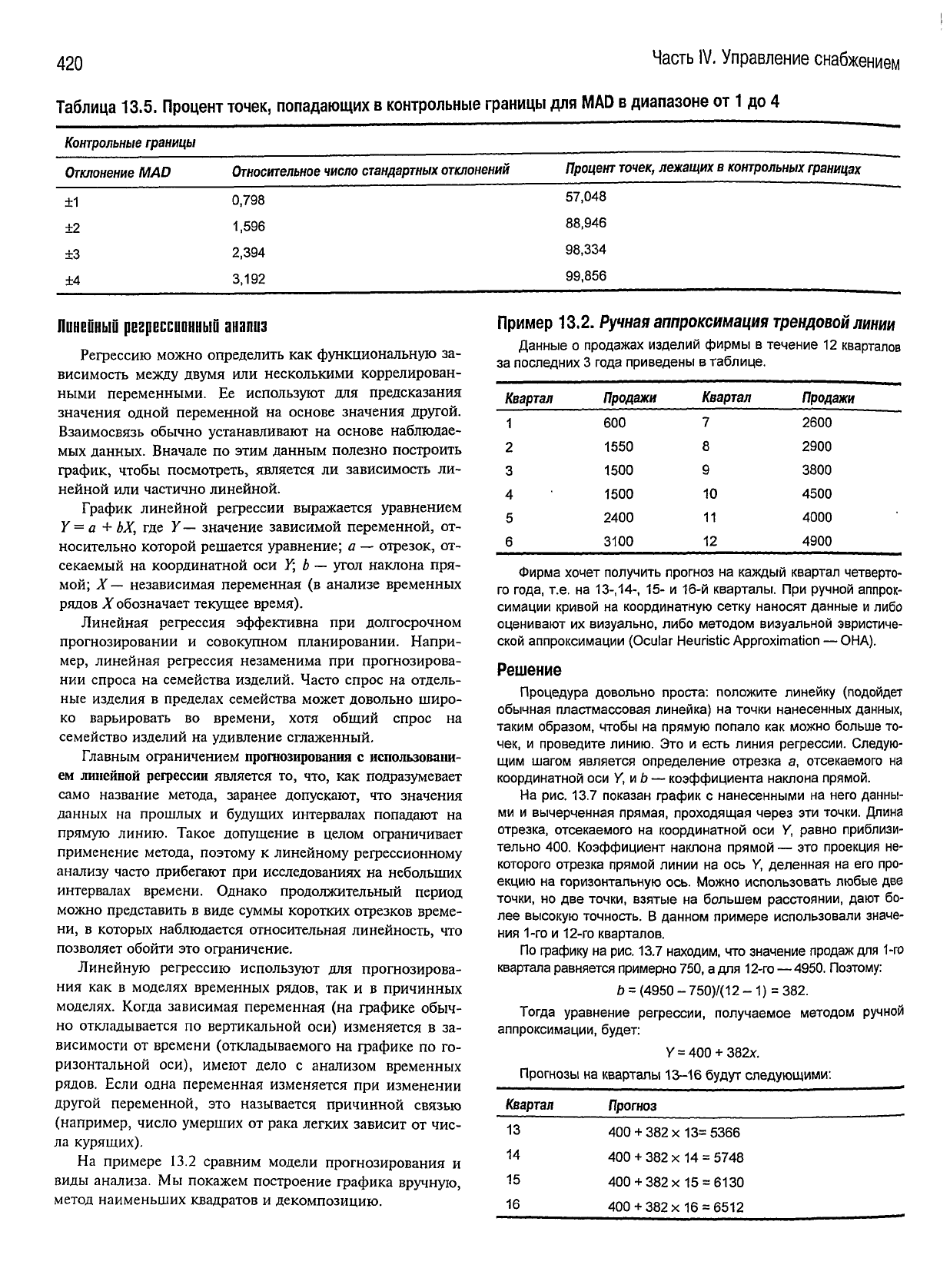
Для большей наглядности строится график. Чтобы по-

казать направление смещения трекинга, на горизонталь-

ной

оси откладывают номер месяца (рис. 13.6).

Обратите внимание, что в приведенном примере тре-

кинг

изменяется от —1 MAD до +3,3 MAD. Это связано с

тем, что текущий спрос оказался выше прогнозируемого в

четырех

из шести периодов. Если бы фактический спрос в

первом периоде не оказался ниже значения прогноза и не

скомпенсировал постоянную положительную ошибку

RSFE,

то трекинг был бы больше и можно было прийти к

заключению, что принятый спрос в 1000 единиц является

неудачным прогнозом.

Для допустимых отклонений трекинга устанавливают

контрольные границы, которые зависят от прогнозируе-

мого спроса (высокодоходные товары или большой объем

продаж

следует

контролировать чаще) и от имеющегося в

распоряжении персонала времени (при суженных допус-

тимых границах больше прогнозов

будет

выходить за эти

границы и поэтому потребуется больше времени для ис-

следований). Учитывая связь трекинга с MAD, по данным

табл. 13.5 можно выбрать контрольные границы по необ-

ходимому

проценту точек, попадающих в область допус-

тимых отклонений MAD.

В правильно сформированной модели прогнозирова-

ния

сумма текущих ошибок прогноза должна быть равна

нулю. Ошибки из-за завышенной оценки компенсируют-

ся

ошибками, вызванными недооценкой. Поэтому тре-

кинг

также должен быть равен нулю, указывая на несме-

щенную модель, а не на опережение или запаздывание

прогноза по отношению к фактическому спросу.

MAD часто используют для прогноза ошибок. Жела-

тельно, чтобы MAD было более чувствительным к послед-

ним

данным. Чтобы достичь этого, вычисляют экспонен-

циально сглаженное MAD как прогноз для диапазона

ошибок

следующего

периода. Процедура аналогична про-

цедуре

однократного экспоненциального сглаживания,

Глава

13.

Прогнозирование

419

уже рассмотренного

этой главе. Значение

MAD

показы-

вает

диапазон ошибки.

При

управлении материальными

запасами

такую

процедуру

с MAD

используют

для

опреде-

ления

уровня резервных запасов,

что

осуществляется

по

такой

формуле:

MAD,=a

\А

1А

F,_,| + (1

a)MAD,_,;

где

MAD, —

прогноз

MAD для /-го

периода;

а —

константа сглаживания (обычно находится

диапа-

зоне

от 0,05 до 0,2);

Д_,

—

фактический спрос

(г

—

1)-го

периода;

•F,_,

—

прогнозируемый спрос

—

1)-го

периода.

Рис.

13.5.

Нормальное

распределение

со

средним,

равным 0 и

MAD,

равным 1

Трекинг

Фактическое

значение

превышает

прогноз

Фактическое

значение

меньше

прогноза

Месяц

Рис.

13.6. График

трекинга,

построенный

по данным

табл.

13.4

Таблица

13.4.

Вычисление

среднего

абсолютного

отклонения

(MAD),

суммы

ошибок

прогноза

(RSFE)

трекинга

(TS) по

прогнозным

фактическим

данным

Месяц

Прогноз

спроса

1000

Фактический

спрос

950

1070

1100

960

1090

1050

Отклонение

-50

+70

+100

-40

+90

+50

RSFE

-50

+20

+120

+80

+170

+220

Абсолютное

отклонение

100

Сумма

абсолютных

отклонений

120

220

260

350

400

MAD*

73,3

66,7

RSFE

MAD

-1

0,33

1,64

1,2

2,4

3,3

*Для

шестого

месяца

MAD

400/6

66,7.

RSFE

*Для

шестого

месяца

TS=-

MAD

220/66,7

3,3 MAD

420

Часть IV

Управление

снабжением

Таблица

13.5. Процент точек, попадающих в контрольные границы для MAD в диапазоне от

до 4

Контрольные

границы

Отклонение

MAD

Относительное

число

стандартных

отклонений

Процент

точек,

лежащих

контрольных

границах

±1

±2

±3

±4

0,798

1,596

2,394

3,192

57,048

88,946

98,334

99,856

Линейный регрессионный анализ

Регрессию можно определить как функциональную за-

висимость

между

двумя

или несколькими коррелирован-

ными

переменными. Ее используют для предсказания

значения

одной переменной на основе значения

другой.

Взаимосвязь обычно устанавливают на основе наблюдае-

мых данных. Вначале по этим данным полезно построить

график, чтобы посмотреть, является ли зависимость ли-

нейной

или частично линейной.

График

линейной регрессии выражается уравнением

= a +

ЬХ,

где Y— значение зависимой переменной, от-

носительно которой решается уравнение; a — отрезок, от-

секаемый на координатной оси Y; b —

угол

наклона пря-

мой;

X — независимая переменная (в анализе временных

рядов

обозначает текущее время).

Линейная

регрессия эффективна при долгосрочном

прогнозировании и совокупном планировании.

Напри-

мер, линейная регрессия незаменима при прогнозирова-

нии

спроса на семейства изделий. Часто спрос на отдель-

ные изделия в

пределах

семейства может довольно широ-

ко

варьировать во времени,

хотя

общий спрос на

семейство изделий на удивление сглаженный.

Главным ограничением прогнозирования с использовани-

ем линейной регрессии является то, что, как подразумевает

само название метода, заранее допускают, что значения

данных на прошлых и

будущих

интервалах попадают на

прямую линию. Такое допущение в целом ограничивает

применение метода, поэтому к линейному регрессионному

анализу часто прибегают при исследованиях на небольших

интервалах времени. Однако продолжительный период

можно представить в виде суммы коротких отрезков време-

ни,

в которых наблюдается относительная линейность, что

позволяет обойти это ограничение.

Линейную регрессию используют для прогнозирова-

ния

как в моделях временных рядов, так и в причинных

моделях. Когда зависимая переменная (на графике обыч-

но

откладывается по вертикальной оси) изменяется в за-

висимости от времени (откладываемого на графике по го-

ризонтальной оси), имеют

дело

с анализом временных

рядов. Если одна переменная изменяется при изменении

другой

переменной, это называется причинной связью

(например,

число умерших от рака легких зависит от чис-

ла курящих).

На

примере 13.2 сравним модели прогнозирования и

виды анализа. Мы покажем построение графика

вручную,

метод

наименьших квадратов и декомпозицию.

Пример 13.2.

Ручная

аппроксимация

трендовой

линии

Данные

продажах изделий фирмы

течение

кварталов

за

последних

года приведены

таблице.

Квартал

Продажи

600

1550

1500

2400

3100

Квартал

Продажи

2600

2900

3800

4500

4000

4900

Фирма

хочет получить прогноз

на

каждый квартал четверто-

го

года,

т.е. на

13-.14-, 15-

и 16-й

кварталы.

При

ручной аппрок-

симации

кривой

на

координатную сетку наносят данные

либо

оценивают

их

визуально, либо методом визуальной эвристиче-

ской

аппроксимации (Ocular Heuristic Approximation

— ОНА).

Решение

Процедура довольно проста: положите линейку (подойдет

обычная пластмассовая линейка)

на

точки нанесенных данных,

таким

образом, чтобы

на

прямую попало

как

можно больше

то-

чек,

проведите линию.

Это и

есть линия регрессии. Следую-

щим

шагом является определение отрезка

а,

отсекаемого

на

координатной

оси

и b

—

коэффициента наклона прямой.

На рис.

13.7

показан график

нанесенными

на

него данны-

ми

вычерченная прямая, проходящая через

эти

точки. Длина

отрезка,

отсекаемого

на

координатной

оси У,

равно приблизи-

тельно 400. Коэффициент наклона прямой

— это

проекция

не-

которого

отрезка прямой линии

на ось У,

деленная

на его

про-

екцию

на

горизонтальную ось. Можно использовать любые

две

точки,

но две

точки, взятые

на

большем расстоянии, дают

бо-

лее высокую точность.

данном примере использовали значе-

ния

1-го и

12-го кварталов.

По графику

на

рис.

13.7 находим,

что

значение продаж для

1-го

квартала равняется

примерно

750, а

для

12-го

—

4950.

Поэтому:

(4950

750)/(12

382.

Тогда уравнение регрессии, получаемое методом ручной

аппроксимации,

будет:

= 400

382х.

Прогнозы

на

кварталы 13-16 будут следующими:

Квартал

Прогноз

400

382x13=5366

400

382

х 14 =

5748

400 +382

6130

400

382x16

6512