Чейз, Ричард, Б., Эквилайн, Николас, Дж., Якобе, Роберт, Ф. Производственный и операционный менеджмент

Подождите немного. Документ загружается.

Глава

15. Системы

управления

товарно-материальными запасами при независимом спросе

471

потребностях в различных изделиях, которые не зависят

один

от

другого.

Например, рабочая станция может вы-

пускать множество деталей, не связанных

между

собой,

но

удовлетворяющих требованиям некоторой "внешней

потребности". Когда же мы говорим о зависимой потреб-

ности,

потребность в каком-то одном изделии выступает

непосредственным следствием потребности в

другом

из-

делии — обычно изделии более высокого уровня, частью

которого оно является.

концептуальной точки зрения, определение зависи-

мой

потребности представляет собой относительно про-

стую

вычислительную

задачу.

Необходимое количество

изделий с зависимой потребностью можно вычислить до-

вольно просто, основываясь на количестве этих изделий в

каждом изделии более высокого уровня. Если, например,

автомобильная компания планирует выпускать 500 авто-

мобилей в день,

тогда

совершенно очевидно, что для

этого ей понадобятся

2000

колес и шин (плюс запасные).

Необходимое количество колес и шин

зависит

от объема

выпускаемой продукции, т.е. оно определяется не незави-

симо.

В то же время потребность в автомобилях

независи-

ма — она определяется множеством факторов, внешних

по

отношению к данной автомобильной компании

(автомобиль не является частью

другой

продукции и по-

требность в автомобилях не связана с потребностью в

других

продуктах).

Чтобы определить количество независимых изделий,

которые необходимо изготовить, фирмы обычно прибегают

услугам

своих отделов сбыта и исследований рынка. Эти

отделы используют ряд методов, в частности опросы потре-

бителей, методы прогнозирования, определение экономи-

ческих и социологических тенденций (см. раздел, посвя-

щенный

прогнозированию, в

главе

13). Поскольку незави-

симая

потребность величина неопределенная, в запас

приходится включать дополнительные изделия. В этой гла-

ве представлены модели для определения количества изде-

лий,

которое необходимо заказать, а также количества до-

полнительных изделий, которое необходимо для гарантиро-

вания

определенного

уровня

обслуживания.

Системы

управления

запасами

Система управления запасами реализует организаци-

онную

структуру

текущую

политику, обеспечивающие

поддержание запаса изделий и эффективное управление

им.

С помощью этой системы осуществляется разработка

графиков

размещения заказов, размещение заказов и по-

лучение материалов и контроль выполнения заказов. Эта

система позволяет отслеживать прохождение заказов и

получать ответы на следующие вопросы: получил ли по-

ставщик

заказ, отгрузил ли он заказанные материалы, со-

блюдаются ли сроки, предусмотрены ли процедуры по-

вторной

выдачи заказов и возврата ненужных или де-

фектных

материалов?

Классификация систем

управления

запасами

Существуют

две основные модели систем управления

товарно-материальными запасами —

модель

фиксиро-

ванным

объемом

(называемая также

модель

экономичного

размера

заказа, или

Q-модель)

модель

фиксированным

периодом

(называемая также

периодической

моделью,

моде-

лью

периодического

контроля,

или

Р-моделью).

Основное

различие

между

ними заключается в сле-

дующем. В модели с фиксированным объемом произво-

дится очередной заказ на поставку, когда запас материала

снижается до определенного уровня. Это событие может

произойти

в любой момент, в зависимости от скорости

потребления

материала. Что же касается модели с

фикси-

рованным

периодом, то в ней осуществляется размещение

очередного заказа через заранее определенный

(контрольный)

период времени.

Использование

модели с фиксированным объемом

(при

которой очередной заказ размещается, когда остаток

запаса снижается до заранее определенного уровня R)

предполагает постоянный контроль остатка запаса. Таким

образом, модель с фиксированным объемом представляет

собой

непрерывно

действующую

систему, которая

требует,

чтобы каждый раз, когда проводится изъятие материалов

из

запаса или добавление их в запас, обновлялись соот-

ветствующие записи и выполнялась проверка, достигнута

ли

точка очередного заказа. В модели с фиксированным

периодом вычисление остатка запаса проводится лишь по

истечении

контрольного периода времени. (Далее мы об-

судим

также некоторые разновидности систем, сочетаю-

щих черты обеих этих моделей.)

Ниже

перечислены некоторые дополнительные разли-

чия,

которые обычно оказывают влияние на выбор той

или

иной системы (табл. 15.1).

• Модель с фиксированным периодом в среднем имеет

больший запас, поскольку запаса материалов должно

хватать

до момента следующей поставки через фиксиро-

ванный

интервал поставок Т. В модели с фиксирован-

ным

объемом никакого фиксирования интервала поста-

вок

не предусматривается, т.е. очередные поставки осу-

ществляются по потребности и дополнительного запаса

на

какой-то период времени создавать не нужно.

• Модель с фиксированным объемом используется для

управления запасами дорогостоящих материалов, по-

скольку она обеспечивает меньший средний размер

запаса.

• Модель с фиксированным объемом больше

подходит

для ответственных (важных) материалов, называемых

критическими,

поскольку в ней предусматривается бо-

лее жесткий контроль за запасами, а следовательно, и

более быстрая реакция на

угрозу

исчерпания запаса.

• Модель с фиксированным объемом имеет большую

трудоемкость обслуживания, поскольку каждое добав-

ление

или изъятие материала должно регистрироваться

системе.

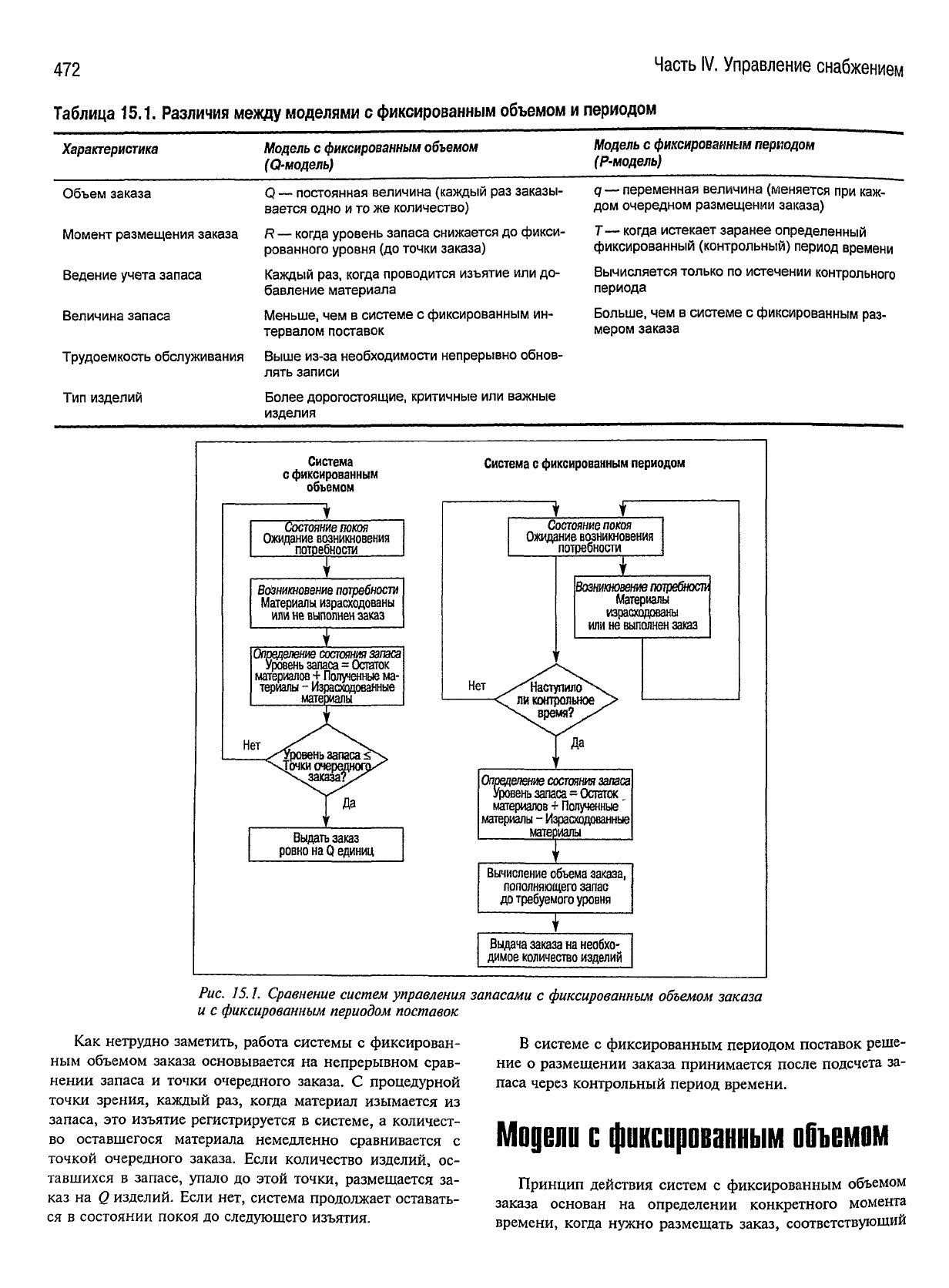
На

рис. 15.1 показано действие каждой из рассматри-

ваемых систем.

472

Часть

IV. Управление снабжением

Таблица

15.1.

Различия

между

моделями

с фиксированным объемом и периодом

Характеристика

Модель

фиксированным

объемом

(Q-модель)

Модель

фиксированным

периодом

(Р-модель)

Объем

заказа

Момент размещения заказа

Ведение

учета

запаса

Величина запаса

Трудоемкость обслуживания

Тип изделий

—

постоянная величина (каждый раз заказы-

вается одно и то же количество)

R —

когда уровень запаса снижается

до

фикси-

рованного уровня (до точки заказа)

Каждый раз, когда проводится изъятие или до-

бавление материала

Меньше, чем

системе

фиксированным ин-

тервалом поставок

Выше из-за необходимости непрерывно обнов-

лять

записи

Более

дорогостоящие,

критичные или важные

изделия

—

переменная величина ((меняется при каж-

дом

очередном размещении заказа)

Т—

когда истекает заранее определенный

фиксированный (контрольный) период времени

Вычисляется только

по

истечении контрольного

периода

Больше, чем

системе

фиксированным раз-

мером

заказа

Система

с фиксированным

объемом

Система

фиксированным периодом

Состояние

ПОКОЙ

Ожидание возникновения

потребности

Возникновение

потребности

Материалы

израсходованы

или

не

выполнен

заказ

Определение

состояния

запаса

уровень запаса

Остаток

материалов

Полученные

ма-

териалы

Израсходованные

материалы

Состояние

покоя

Ожидание возникновения

потребности

Возникновение

потребности

Материалы

израсходованы

или

не

выполнен

заказ

Нет

Наступило

ли контрольное

время?

Да

Выдать

заказ

ровно

на Q

единиц

Определение

состояния

запаса

Уровень

запаса=Остаток,

материалов

Полученные

материалы

Израсходованные

материалы

Вычисление

объема

заказа,

пополняющего запас

до требуемого уровня

Выдача

заказа

на

необхо-

димое количество изделий

Рис.

15.1. Сравнение систем управления запасами с фиксироеанньш

объемом

заказа

и с фиксироеанньш

периодом

поставок

Как

нетрудно заметить, работа системы

фиксирован-

ным

объемом заказа основывается

на

непрерывном срав-

нении

запаса

точки очередного заказа.

процедурной

точки зрения, каждый

раз,

когда материал изымается

из

запаса,

это

изъятие регистрируется

системе,

количест-

во оставшегося материала немедленно сравнивается

точкой очередного заказа. Если количество изделий,

ос-

тавшихся

запасе, упало

до

этой точки, размещается

за-

каз

на Q

изделий. Если нет, система продолжает оставать-

ся

состоянии покоя

до

следующего

изъятия.

системе

фиксированным периодом поставок реше-

ние

размещении заказа принимается после подсчета

за-

паса через контрольный период времени.

Модели

с фиксированным оОъемом

Принцип

действия систем

фиксированным объемом

заказа основан

на

определении конкретного момента

времени, когда нужно размещать заказ, соответствующий

Глава

15.

Системы

управления

товарно-материальными

запасами

при

независимом

спросе

473

определенному уровню запаса (точке заказа),

— Л, а так-

же размера этого заказа

Точка заказа

R — это

всегда

совершенно

определенное количество материала. Заказ

размером

размещается

в тот

момент, когда уровень

за-

паса достигает точки

R. Уровень

запаса

(Inventory Position)

определяется

как

остаток материалов перед прошлой

по-

ставкой,

плюс количество полученных материалов

при

прошлой

поставке, минус израсходованное количество.

Решение,

принимаемое

моделях

фиксированным

объ-

емом,

можно сформулировать, например, так: "когда

уро-

вень

запаса снижается

до 36,

разместить заказ

на 57 до-

полнительных единиц материала".

Действие модели

фиксированным объемом можно

уп-

рощенно

описать исходя

из

предположения,

что все

харак-

теристики движения запасов доподлинно известны.

На-

пример,

если годовая потребность

каком-то изделии рав-

на

1000

штук,

то

это именно 1000 штук,

не

1000

±10%.

То

же самое можно сказать

затратах

на

размещение заказа

(или

пуско-наладочных затратах)

издержках хранения

за-

пасов.

Несмотря

на

то,

что

предположение

полной опре-

деленности далеко

не

всегда реально,

оно

дает

хорошую

основу для описания моделей движения запасов.

Рассмотрим определение оптимальной величины зака-

за, используя упрощенную модель, приведенную

на

рис.

15.2, и

следующие допущения. (Эти допущения,

ко-

нечно,

далеки

от

реальности,

но они

могут

служить

от-

правной

точкой

позволяют

нам

воспользоваться

до-

вольно простыми примерами.)

•

Потребность

материале постоянна

равномерно

распределена

по

всему периоду.

•

Время выполнения заказа (время

момента выдачи

за-

каза

до получения заказанных материалов) неизменно.

•

Цена единицы материалов постоянна.

•

Издержки хранения запасов рассчитываются

по

сред-

ней

величине запаса.

•

Затраты

на

размещение заказа

пуско-наладочные

за-

траты постоянны.

•

Для

закупок любых количеств материала имеются

не-

обходимые ресурсы

исключается возможность невы-

полнения

заказа.

Текущий

^наличный)

запас

[К

Q-

Время

Рис. 15.2.

Основная

модель

системы

фиксированным

объе-

мом

Текущий запас материала,

как

показано

на рис. 15.2,

изменяется

по

"пиле"

и, при его

снижении

до

уровня

(точка заказа), размещается повторный заказ. Заказанные

изделия

будут

получены через интервал времени

кото-

рый

данной модели остается неизменным.

Вначале

для

разработки модели управления запасами

необходимо установить функциональную взаимосвязь

между

интересующими

нас

переменными.

данном

слу-

чае

нас

интересуют общие затраты

на

создание запасов,

которые можно выразить следующим уравнением:

Суммарные годовые затраты

Годовые затраты

на

закупки

Годовые затраты

на

размещение заказов

Годовые затраты

на

хранение

или

(15.1)

где

ТС — суммарные годовые затраты;

—

годовая потребность

материале;

— цена единицы закупаемого материала;

Q — количество материала, которое необходимо зака-

зать. Оптимальное количество называется

экономичным

размером

заказа (Economic Order Quantity

— EOQ, или

О,,,);

— затраты

на

размещение одного заказа;

—

точка повторного заказа;

—

период выполнения заказа;

Я—

годовые издержки хранения единицы среднего

запаса материала. Зачастую затраты

на

хранение опреде-

ляются

как

процент

от

цены материала,

т.е. Н =

/С,

где

— процент

от

цены

С.

правой части уравнения представляет собой

стоимость закупки годовой потребности материала;

(D/Q)S—

годовые затраты

на

размещение заказов

(фактическое

количество размещенных заказов

D/Q, ум-

ноженное

на

затраты

на

размещение одного заказа

5), а

(Q/2JH

— годовые издержки хранения (средний запас

Q/2, умноженный

на

годовые издержки хранения одного

изделия

Н).

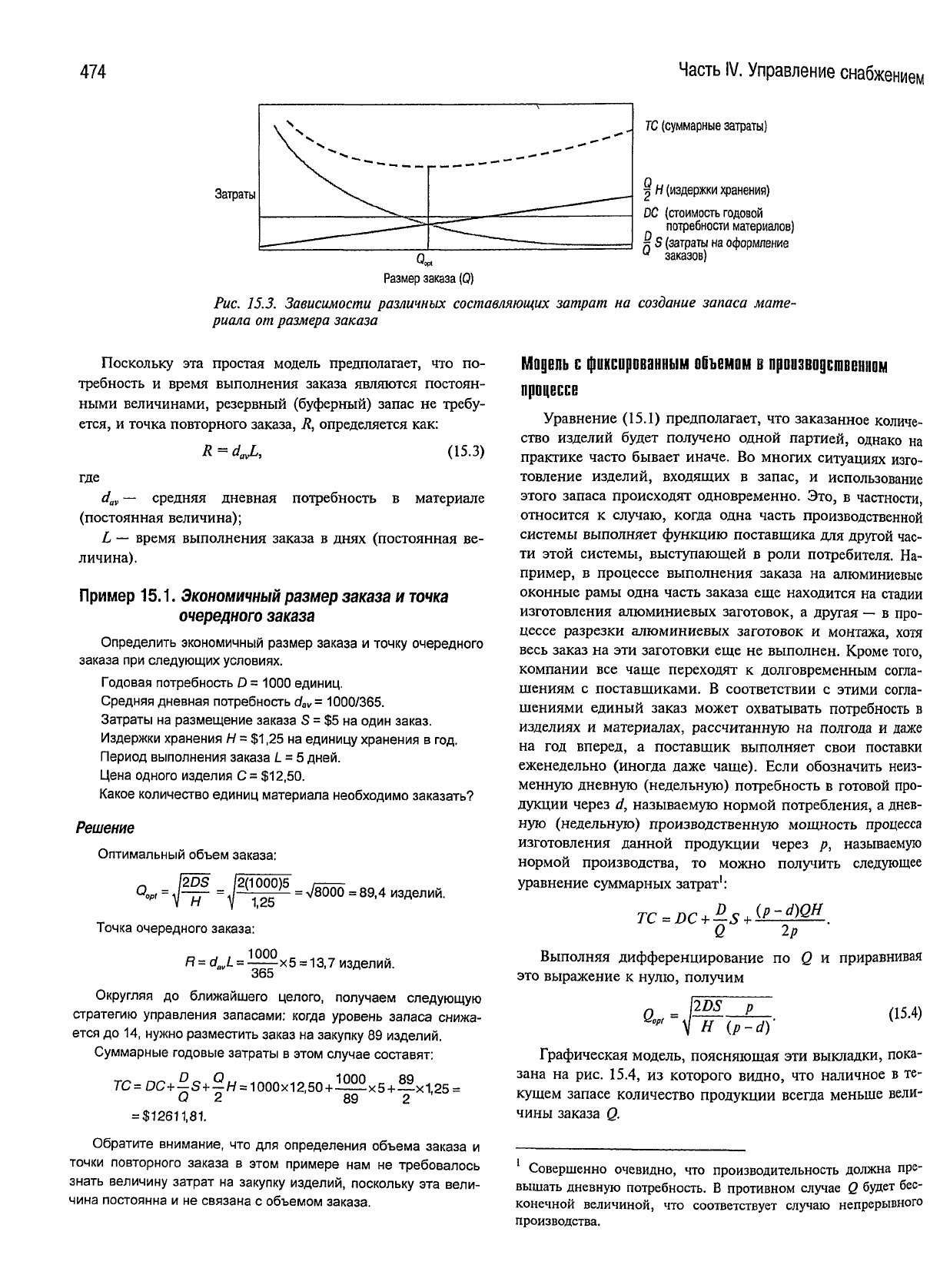
Зависимости

между

этими величинами пред-

ставлены

графическом виде

на

рис.

15.3.

Затем

для

разработки модели управления запасами

не-

обходимо определить

ту

величину заказа

apr>

при

которой

суммарные затраты минимальны.

На

рис.

15.3

суммарные

затраты достигают минимума

точке,

где

тангенс

угла

наклона

кривой суммарных годовых затрат равен нулю.

Для нахождения точки минимальных затрат возьмем

про-

изводную

от

суммарных годовых затрат

по Q и

приравня-

ем

ее к

нулю.

Для

рассматриваемого здесь уравнения

эти

преобразования

будут

иметь следующий

вид:

£-ЙгК-

(15.2)

474

Часть

IV.

Управление

снабжением

„ 1С (суммарные

затраты)

Затраты

\^ _J\ 5

(издержки

хранения)

DC (стоимость годовой

потребности

материалов)

(затраты

на

оформление

заказов)

Размер

заказа (О)

Рис. 15.3. Зависимости

различных

составляющих

затрат на

создание

запаса

мате-

риала

от

размера

заказа

Поскольку

эта простая модель предполагает, что по-

требность и время выполнения заказа являются постоян-

ными

величинами, резервный (буферный) запас не требу-

ется, и точка повторного заказа, R, определяется как:

R=d

L, (15.3)

где

— средняя дневная потребность в материале

(постоянная

величина);

— время выполнения заказа в днях (постоянная ве-

личина).

Пример

15.1.

ЭКОНОМИЧНЫЙ размер заказа

точка

очередного

заказа

Определить

экономичный размер заказа и точку очередного

заказа при

следующих

условиях.

Годовая

потребность D = 1000 единиц.

Средняя

дневная

потребность

1000/365.

Затраты

на размещение заказа S = $5 на один заказ.

Издержки

хранения

Н = $1,25 на единицу

хранения

в год.

Период

выполнения

заказа L = 5 дней.

Цена

одного изделия С = $12,50.

Какое количество единиц

материала

необходимо заказать?

Решение

Оптимальный

объем

заказа:

Точка

очередного заказа:

1000

" 365

= 78000 =89,4 изделий.

х5 =13,7 изделий.

Округляя

до ближайшего целого,

получаем

следующую

стратегию

управления

запасами: когда уровень запаса снижа-

ется до 14, нужно разместить заказ на закупку 89 изделий.

Суммарные

годовые

затраты

в этом

случае

составят:

DC+^S+-5H

1000X1250

±X5

Q 2

= $12611,81.

х1,25

Обратите

внимание, что для определения

объема

заказа и

точки повторного заказа в этом примере нам не

требовалось

знать

величину

затрат на закупку изделий, поскольку эта вели-

чина

постоянна и не связана с объемом заказа.

Модель

фиксированным оОъемам

производственном

процессе

Уравнение (15.1) предполагает, что заказанное количе-

ство изделий

будет

получено одной партией, однако на

практике

часто бывает иначе. Во многих ситуациях изго-

товление изделий, входящих в запас, и использование

этого запаса происходят одновременно. Это, в частности

относится к случаю, когда одна часть производственной

системы выполняет функцию поставщика для другой час-

ти этой системы, выступающей в роли потребителя. На-

пример,

в процессе выполнения заказа на алюминиевые

оконные

рамы одна часть заказа еще находится на стадии

изготовления алюминиевых заготовок, а другая — в про-

цессе разрезки алюминиевых заготовок и монтажа, хотя

весь заказ на эти заготовки еще не выполнен. Кроме того,

компании

все чаще переходят к долговременным согла-

шениям

с поставщиками. В соответствии с этими согла-

шениями

единый заказ может охватывать потребность в

изделиях и материалах, рассчитанную на полгода и даже

на

год вперед, а поставщик выполняет свои поставки

еженедельно (иногда даже чаще). Если обозначить неиз-

менную дневную (недельную) потребность в готовой про-

дукции через d, называемую нормой потребления, а днев-

ную (недельную) производственную мощность процесса

изготовления данной продукции через р, называемую

нормой

производства, то можно получить следующее

уравнение суммарных затрат

-S

Q 1р

Выполняя

дифференцирование по Q и приравнивая

это

выражение к нулю, получим

—.

(15.4)

(p-d)

Графическая модель, поясняющая эти выкладки, пока-

зана

на рис. 15.4, из которого видно, что наличное в те-

кущем запасе количество продукции всегда меньше вели-

чины

заказа Q.

Совершенно очевидно, что производительность должна пре-

вышать дневную потребность. В противном

случае

будет

бес-

конечной величиной, что соответствует

случаю

непрерывного

производства.

Глава 15. Системы управления товарно-материальными запасами при независимом спросе

475

Число

единиц

текущем

запасе

Приращение

Производство

Нппмя

пппич-

потребление

водсИорма одновременно^

7п

ебЛ

НИ

Уч/

Норма

х^потребления

Производства

нет;

только

"ч^

/-потребление

1 !\/

•- i

Время

Рис. 15.4.

Движение

запаса

готовой

продукции

случае

моде-

ли с

фиксированным

объемом

производственном

процессе

Пример

15.2.

Оптимальный

размер

производства

пар-

тип продукции

Продукт

X—

это типичное изделие

товарно-материальном

запасе

фирмы.

Окончательная

сборка этого изделия выполня-

ется

на

ежедневно работающей сборочной линии. Один

компо-

нент изделия

(назовем его

X-i)

изготавливается

другом

под-

разделении.

Выпуская компоненты

Хь это

подразделение обес-

печивает производительность, составляющую

100

изделий

день. Потребность

компоненте

Xi на

сборочной линии равна

штук в день.

Каким

будет оптимальный размер производства партии

для

компонента

X»,

если заданы следующие условия:

Ежедневный норма потребления

изделий.

Годовая потребность

D =

10 000 (40 изделий

250

рабочих дней).

Дневная норма производства

р =

100 изделий.

Затраты

на

пуско-наладочные работы

= $50.

Годовые

издержки

хранения

= $0,50

на

одно изделие.

Стоимость одного компонента

составляет

С =

$7.

Время упреждения заказа

L =

дней.

Решение

Оптимальный размер производства партии компонентов

точка очередного заказа вычисляются следующим способом:

100

2£S_P_

2x10000x50

V Н (p-d) V °'

(ЮО-40)

= dL = 40x7 = 280 изделий.

Отсюда следует,

что

заказ

на 1826

штук компонента

Xi не-

обходимо размещать

момент, когда текущий запас снижается

до 280 штук.

Учитывая,

что

норма производства компонента

составля-

ет

100

изделий

день, выполнение этого заказа займет

18,26

дней

обеспечит 45,65-дневный запас (1826/40).

период,

ко-

гда

компонент

Xi не

выпускается (27,39 дней), подразделение

может выполнять другие заказы.

Определение уровня резервного запаса

Описанная

нами модель управления запасами предпо-

лагала, что потребность известна и постоянна. Однако в

большинстве случаев потребность является переменной

величиной, изменяясь ежедневно. В связи с этим необхо-

димо иметь и поддерживать так называемый резервный

(буферный) запас, обеспечивая определенный уровень

защиты от дефицита изделий.

Резервный

запас

(Safety

Stock) можно определить как величину запаса, постоянно

поддерживаемую дополнительно к ожидаемой потребно-

сти. В

случае

нормального распределения колебаний по-

требности это

будет

среднее значение отклонений. Если,

например,

среднемесячная потребность составляет 100

изделий и мы предполагаем, что в следующем месяце она

останется такой же, а запас составляет 120 изделий, то 20

изделий и

будут

резервным запасом.

В литературе, посвященной определению резервного

запаса, встречаются два подхода к установлению потреб-

ности в запасе, обеспечивающем защиту. Первый под-

ход — это расчет через

вероятность

того, что потребность

превысит определенную величину. Можно, например, по-

ставить

следующую

задачу:

установить такой уровень ре-

зервного запаса, чтобы вероятность того, что потребность

превысит 300 изделий, была не выше 5%. Второй подход

основывается на определении ожидаемого количества из-

делий, которых может не хватить. Например, можно по-

ставить перед собой

задачу:

установить такой уровень за-

паса, чтобы можно было удовлетворять не менее чем 95%

заказов на данную продукцию, т.е. дефицит изделий

будет

существовать в течение лишь 5% всего времени. Еще раз

подчеркнем, что в первом подходе речь идет о

вероятно-

сти превышения определенного значения, а во втором —

том,

сколько

изделий нам не

хватает.

Вероятностный

подход.

Использование вероятностного

критерия для определения резервного запаса представляет

собой довольно простую

задачу.

С учетом моделей, опи-

санных в этой главе, мы предполагаем, что потребность

на

протяжении определенного периода времени имеет

нормальное распределение, характеризующееся некото-

рым средним значением и стандартным отклонением.

Напоминаем,

что в

этом

подходе

рассматривается

лишь

вероятность

исчерпания

запаса,

а не

количество

изделий,

которых

не хватит. Чтобы определить вероятность ис-

черпания запаса за данный период времени, можно про-

сто построить график нормального распределения для

ожидаемой потребности и установить, какой точке кривой

распределения соответствует имеющееся в наличии коли-

чество продукции.

Чтобы проиллюстрировать этот подход, рассмотрим

несколько простых примеров. Допустим, ожидается, что в

течение следующего месяца потребность в определенных

изделиях составит 100 штук. Кроме того, нам известно,

что стандартное отклонение равно 20 штук. Если мы по-

дойдем к началу этого месяца, имея в запасе лишь 100

476

Часть

IV. Управление снабжением

изделий, то вероятность исчерпания запаса составит 50%.

Для половины месяцев года мы предполагаем, что наша

потребность превысит 100 изделий; для другой половины

месяцев мы предполагаем, что наша потребность

будет

меньше 100 изделий. Далее, если мы

будем

делать одно-

разовый заказ на месячный запас изделий в количестве

100 штук и получать эту партию в начале месяца, то мож-

но

ожидать, что 6 месяцев в

году

мы

будем

испытывать

дефицит изделий (т.е. исчерпывать свой запас).

Если нам кажется, что столь частое исчерпание запаса

изделий неприемлемо, нам потребуется дополнительный

запас,

который позволит снизить риск исчерпания запаса.

Один из возможных вариантов — хранить дополнитель-

ные 20 единиц изделий. В этом

случае

мы по-прежнему

будем

делать одноразовый заказ на месячный запас изде-

лий,

однако график поставки изделий должен быть таким,

чтобы они поступали к нам в тот момент, когда у нас в

запасе еше остаются 20 изделий. Это обеспечивает нам

небольшой буфер (резерв) изделий, позволяющий снизить

вероятность исчерпания запаса. Если бы стандартное от-

клонение,

характеризующее нашу потребность в издели-

ях, равнялось 20, мы поддерживали бы резервный запас,

равный величине стандартного отклонения. Воспользо-

вавшись таблицей стандартного нормального распределе-

ния

(Приложение D) и сместившись на одно стандартное

отклонение вправо от среднего значения, получим веро-

ятность, равную

0,8413.

(Из таблицы мы получаем значе-

ние

0,3413,

к которому надо добавить 0,5.) Итак, в тече-

ние

приблизительно 84% всего времени мы рассчитываем

на

то, что наш запас не исчерпается, однако в течение

16% времени мы

будем

испытывать дефицит изделий. Ес-

ли мы

будем

заказывать изделия каждый месяц, можно

ожидать, что дефицит изделий

будет

ощущаться примерно

2 месяца в

году

(0,16 х 12 =

1,92).

Обычно компании, использующие этот подход, устанав-

ливают вероятность "неисчерпания" запаса равной 95%. В

нашем примере это означает, что резервный запас должен

составлять примерно 1,64 стандартного отклонения, или 33

изделия (1,64 х 20 = 32,8). Это вовсе не означает,

будто

ка-

ждый месяц мы должны заказывать дополнительных 33 из-

делия. Это означает только, что каждый раз мы должны за-

казывать месячный запас изделий, однако график получе-

ния

их необходимо спланировать таким образом, чтобы в

момент поступления заказанной партии изделий мы могли

рассчитывать на наличие у себя в запасе 33 изделий. В этом

случае

можно рассчитывать на то, что дефицит изделий бу-

дет ощущаться лишь в течение 0,6 месяца в

году

(иными

словами, запас

будет

исчерпываться лишь в одном месяце

из

каждых 20).

Подход, основанный на понятии "уровень обслужива-

ния".

Попытаемся выявить недостатки вероятностного

подхода к определению резервного запаса, воспользовав-

шись следующей аналогией. Допустим, метеоролог про-

гнозирует, что завтра

будет

дождь. Устроит ли вас прогноз

типа "да/нет"

(будет

дождь/не

будет

дождя) или вы пред-

почли бы некоторые подробности (например, о каком

дожде

идет речь:

чуть-чуть

покапает или

будет

лить как из

ведра, а может быть, начнется настоящий потоп)? А если

сейчас зима, и метеоролог просто обещает, что завтра

пойдет снег, — вас устроит такой прогноз (даже если он

сбудется с большой вероятностью)? Может быть, вы

предпочли бы знать,

будет

ли это легкий снежок или на-

стоящий снежный буран, который приведет к возникно-

вению автомобильных "пробок" на дорогах и закрытию

аэропортов? В этом и кроется идея этой модели запасов.

Нас

интересует не только вероятность исчерпания запаса

(вероятность дождя или снега), но и скольких изделий

нам

будет

недоставать (интенсивность дождя или снега).

Итак,

мы готовы к тому, чтобы дать определение

уровня обслуживания. Уровень обслуживания

(Service

Level)

в нашем рассмотрении обозначает требуемое коли-

чество изделий, которое можно реально получить из на-

личного запаса. Если, например, годовая потребность в

каком-то изделии составляет 1000 штук, то 95%-ный уро-

вень обслуживания означает, что 950 штук можно немед-

ленно

получить из запаса, а 50 штук не хватит. (Эта мо-

дель неприменима в тех случаях, когда всю

годовую

по-

требность можно определить лишь небольшим числом

потребителей, поскольку использовать для описания мо-

дели нормальное распределение допустимо только при

достаточно большом числе точек.)

Предложенная нами концепция уровня обслуживания

основана на статистической характеристике, известной

как

"Ожидаемое z или

E(z)

'•

E(z) — это ожидаемое коли-

чество изделий, которых

будет

не

хватать

на протяжении

каждого интервала времени выполнения заказа. В данном

случае

предполагается, что потребность имеет нормальное

распределение.

Чтобы вычислить уровень обслуживания, необходимо

знать,

сколько

изделий не

хватает.

Предположим, напри-

мер, что средняя недельная потребность в определенном

изделии равна 100 штук и стандартное отклонение — 10

штук. Если в начале недели мы располагаем 110 изделия-

ми,

сколько изделий нам может не

хватить?

Чтобы отве-

тить на этот вопрос, нужно просуммировать вероятность

того, что нам потребуется 111 изделий (не

хватает

одного

изделия),

вероятность того, что потребуется 112 изделий

(не

хватает

двух

изделий), вероятность того, что потребу-

ется 113 изделий (не

хватает

трех

изделий), и т.д. Сумми-

рование даст нам количество изделий, которых, по наше-

му мнению, может не хватить, если запас составит ПО

изделий.

Несмотря на то, что сама по себе эта концепция доста-

точно проста, соответствующие уравнения решить вручную

невозможно. К счастью, Роберт Браун (Robert Brown) со-

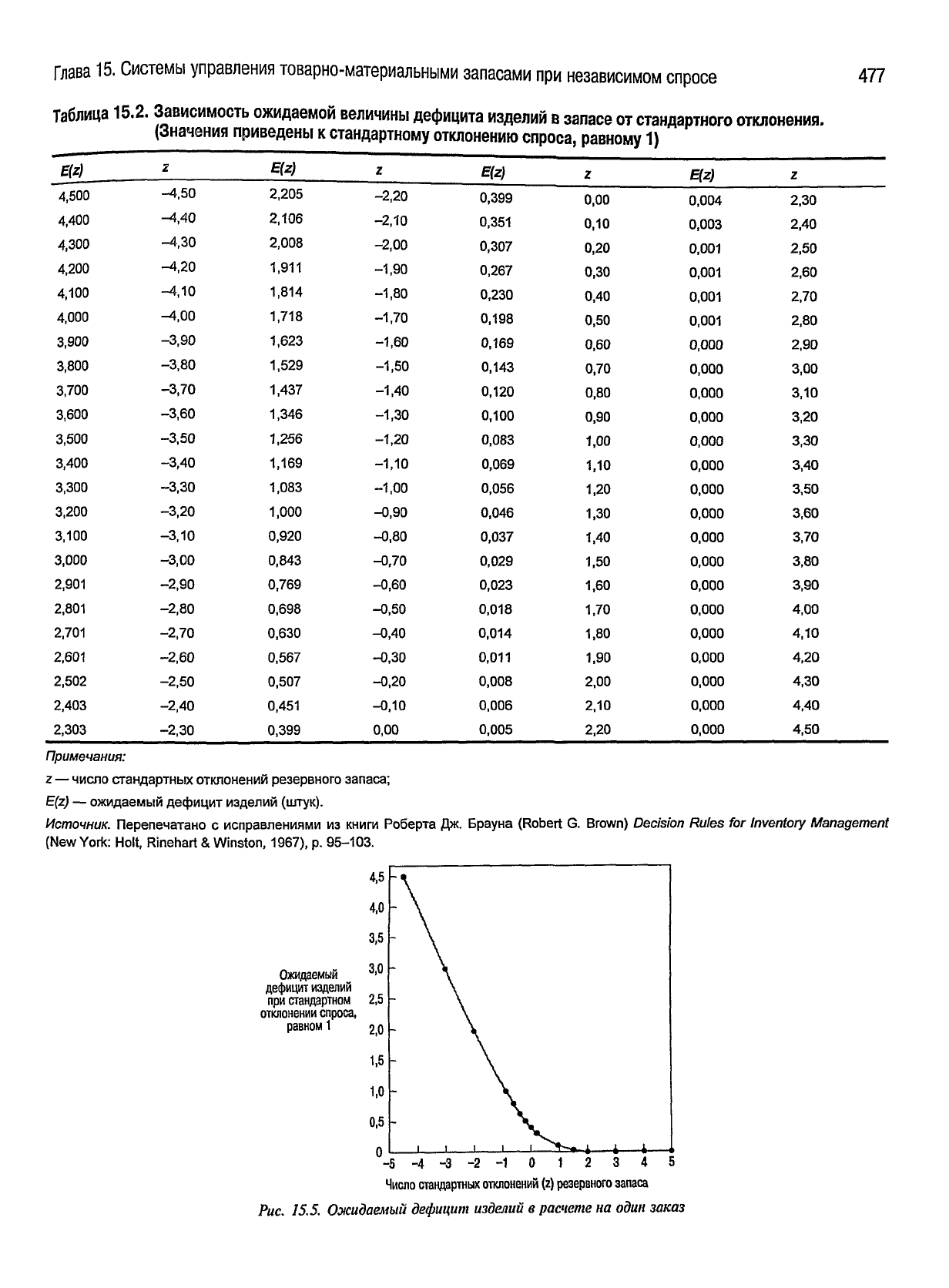
ставил таблицы ожидаемых значений (табл. 15.2).

На

рис. 15.5 показано графическое представление дан-

ных из табл. 15.2. С помощью этого графика можно опре-

делить ожидаемый дефицит изделий в каждом цикле вы-

полнения

заказа (это применимо и к Р-, и к (^-моделям).

Глава 15. Системы управления товарно-материальными запасами при независимом спросе

Таблица

15.2.

Зависимость ожидаемой

величины

дефицита изделий

запасе от стандартного отклонения.

(Значения

приведены

стандартному

отклонению

спроса,

равному

477

B(z)

4,500

4,400

4,300

4,200

4,100

4,000

3,900

3,800

3,700

3,600

3,500

3,400

3,300

3,200

3,100

3,000

2,901

2,801

2,701

2,601

2,502

2,403

2,303

-4,50

-4,40

-4,30

-4,20

-4,10

-4,00

-3,90

-3,80

-3,70

-3,60

-3,50

-3,40

-3,30

-3,20

-3,10

-3,00

-2,90

-2,80

-2,70

-2,60

-2,50

-2,40

-2,30

E(z)

2,205

2,106

2,008

1,911

1,814

1,718

1,623

1,529

1,437

1,346

1,256

1,169

1,083

1,000

0,920

0,843

0,769

0,698

0,630

0,567

0,507

0,451

0,399

-2,20

-2,10

-2,00

-1,90

-1,80

-1,70

-1,60

-1,50

-1,40

-1,30

-1,20

-1,10

-1,00

-0,90

-0,80

-0,70

-0,60

-0,50

-0,40

-0,30

-0,20

-0,10

0,00

E(z)

0,399

0,351

0,307

0,267

0,230

0,198

0,169

0,143

0,120

0,100

0,083

0,069

0,056

0,046

0,037

0,029

0,023

0,018

0,014

0,011

0,008

0,006

0,005

0,00

0,10

0,20

0,30

0,40

0,50

0,60

0,70

0,80

0,90

1,00

1,10

1,20

1,30

1,40

1,50

1,60

1,70

1,80

1,90

2,00

2,10

2,20

0,004

0,003

0,001

0,000

2,30

2,40

2,50

2,60

2,70

2,80

2,90

3,00

3,10

3,20

3,30

3,40

3,50

3,60

3,70

3,80

3,90

4,00

4,10

4,20

4,30

4,40

4,50

Примечания:

—

число

стандартных

отклонений

резервного

запаса;

E(z)

—

ожидаемый

дефицит

изделий

(штук).

Источник.

Перепечатано

исправлениями

из

книги

Роберта

Дж.

Брауна

(Robert

Brown) Decision

Rules

for

Inventory Management

(New

York:

Holt,

Rinehart

Winston,

1967),

95-103.

4,5

4,0

3,5

Ожидаемый

дефицит

изделий

при стандартном

2,5

отклонении спроса,

равном

1,5

1,0

0,5

-5-4-3-2-1

0 1 2 3 4

Число

стандартных

отклонений (z) резервного запаса

Рис. 15.5.

Ожидаемый

дефицит

изделий

расчете

на

один

заказ

478

Часть

IV.

Управление

снабжением

Воспользовавшись нашим предыдущим примером,

предположим, что средняя потребность равна 100 изделий,

а стандартное отклонение для этой потребности равно 10

штук. Если мы хотим воспользоваться рис. 15.5, значения

вертикальной оси нужно умножить на 10, поскольку этот

график

построен при стандартном отклонении, равном од-

ному изделию. Пользуясь числами, показанными в

табл. 15.2, или их графическим представлением на рис. 15.5

при

1 и при условии, что наш резервный запас состав-

ляет 10 изделий, можно рассчитывать на дефицит 0,83 из-

делий

(0,083

умножить на 10, поскольку рисунок и таблица

построены для стандартного отклонения, равного 1). По-

скольку нормальная потребность в течение этого периода

равняется 100, а нам не

хватает

лишь 0,83 изделий (т.е.

меньше одного изделия), наш уровень обслуживания рав-

няется

100 - 0,83, или

99,17%.

Если в том же примере у нас не

будет

никакого ре-

зервного запаса (т.е. заказываем точно 100 изделий), мы

будем

испытывать дефицит 3,99 изделий

(0,399

умножить

на

10). А наш уровень обслуживания

будет

равен 100 —

3,99, или 96,01%.

Из

этого примера также

следует,

что, если мы поддер-

живаем резервный запас, равный минус одному стандарт-

ному отклонению, то это говорит лишь о том, что мы

располагаем в начале каждой недели не 100 изделиями, а

90. При 90 изделиях мы

будем

испытывать дефицит 10,83

изделий, а наш уровень обслуживания

будет

равняться

89,17%.

Если же в начале каждой недели у нас

будет

изделий, мы

будем

испытывать дефицит

20,08

изделий, а

если 70 — то 30 изделий и т.д. Поскольку табл. 15.2 и

рис.

15.5 основаны на стандартном отклонении спроса,

равном одному изделию, от нас

требуется

лишь умножать

соответствующие числа на фактически используемые

данные. Еще один пример: если потребность составляет

550 изделий, а стандартное отклонение равно 36 изделий,

то наличие 568 изделий

даст

стандартное отклонение ре-

зервного запаса, равное 0,5, причем ожидаемая величина

дефицита изделий составит 0,198 х 36 = 7,128 штук. Сле-

довательно, уровень обслуживания составит (550 —

7,128)/550

98,7%.

Подводя итог предыдущего обсуждения

подхода,

осно-

ванного на использовании понятия "уровень обслужива-

ния",

можно отметить следующее: было приведено стан-

дартное отклонение, связанное с соответствующей по-

требностью, по основанию 1 (одна единица). Затем с

помощью табл. 15.2 мы вычислили планируемый дефицит

изделий для конкретного уровня обслуживания. В

случае

вероятностного

подхода

к исчерпанию запаса мы непо-

средственно использовали стандартное нормальное рас-

пределение (Приложение D), чтобы определить число

стандартных отклонений резервного запаса, требующееся

для достижения нужной нам вероятности. Главное пре-

имущество

подхода,

основанного на использовании

поня-

тия

"уровень обслуживания", заключается в том, что ре-

зервный запас определяется на основании фактического

количества изделий, которые мы хотим поставить нашим

потребителям.

Мы

продолжим это объяснение в контексте

двух

базо-

вых моделей — с фиксированным объемом заказа и с

фиксированным

периодом поставок. Мы осветим также

важные вопросы, касающиеся способов проектирования

таких систем управления запасами, которые обеспечивали

бы приемлемые уровни обслуживания потребителей, ми-

нимизируя при этом затраты на поддержание запаса. В

приводимых примерах мы продемонстрируем

подход

вычислению резервного запаса, основанный на использо-

вании

уровня обслуживания. Для тех, кто предпочитает

пользоваться подходом, основанным на вероятности ис-

черпания запаса, укажем, что широко распространенными

значениями

z являются 1,64 для 95%-ной вероятности и

2,0 для 98%-ной вероятности.

Модель

с фиксированным объемом и уровень обслуживания

Модель с фиксированным объемом заказа непрерывно

отслеживает уровень запаса и размещает новый заказ,

когда запас достигает некоторого уровня R. Опасность ис-

черпания запаса в этой модели возникает только в тече-

ние

времени выполнения заказа, т.е. периода

между

мо-

ментом размещения заказа и моментом получения изде-

лий

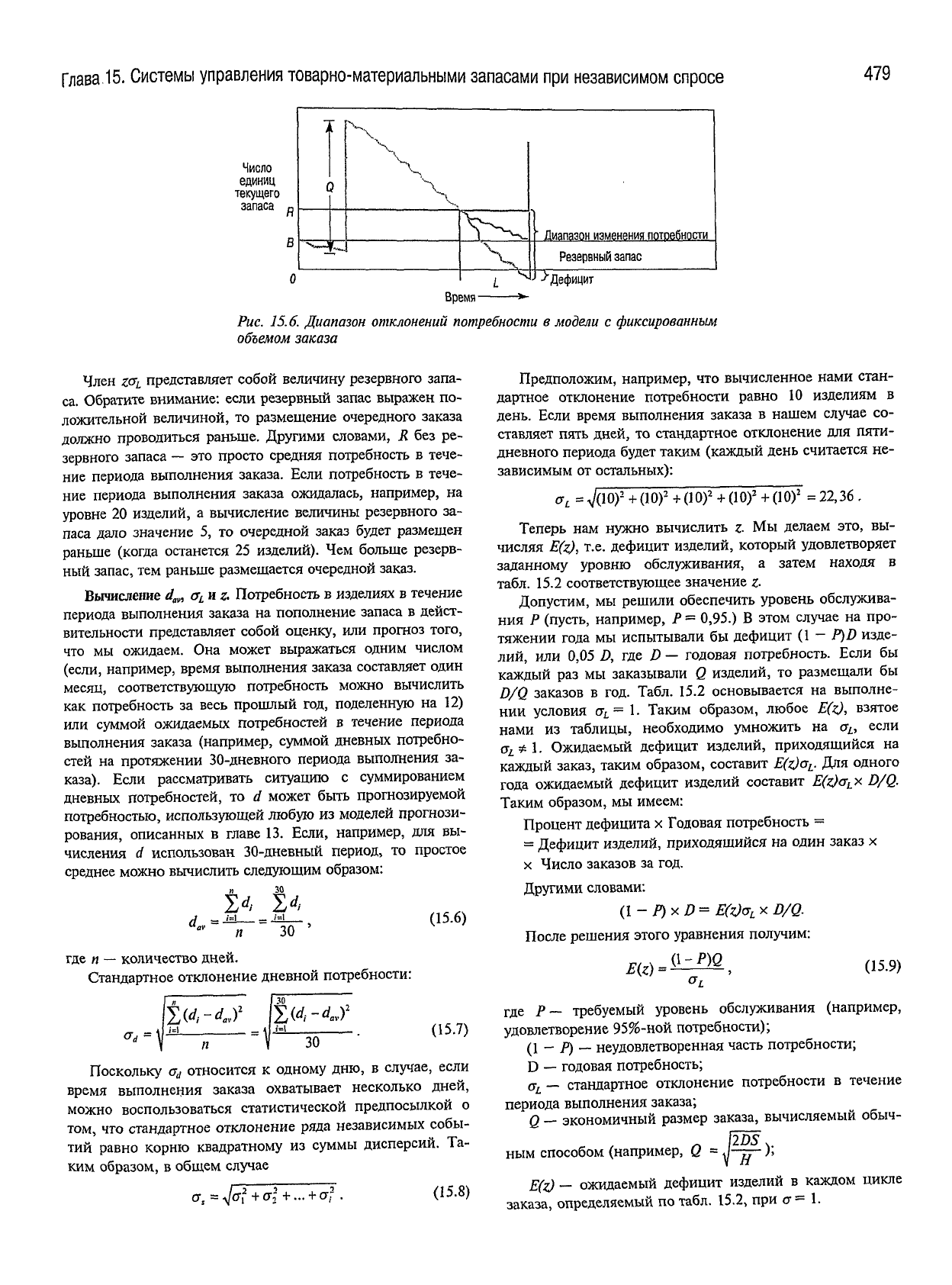
по этому заказу. Как показано на рис. 15.6, заказ

размещается в тот момент, когда уровень запаса снижает-

ся

до точки повторного заказа R.

В течение времени выполнения заказа L возможны

изменения

потребностей в определенном диапазоне. Этот

диапазон вычисляется либо на основе анализа данных,

отражающих прошлые потребности, либо на основе

неко-

торой предположительной оценки (если данные за про-

шедший период невозможно получить).

Величина резервного запаса зависит, как уже указыва-

лось, от

требуемого

уровня обслуживания. Количество из-

делий Q, которые необходимо заказать, вычисляется

обычным способом (учитывая потребность, издержки,

связанные с дефицитом, затраты на размещение заказа,

затраты на хранение и т.п.). Затем устанавливается точка

очередного заказа, которая

учитывает

ожидаемую потреб-

ность в течение периода выполнения заказа, плюс ре-

зервный запас, определяемый требуемым уровнем

обслу-

живания.

Таким

образом,

важнейшее

различие

между

моде-

лью, в

которой

потребность

известна,

такой,

которой

потребность

неизвестна,

заключается

определении

точки

очередного

заказа.

Объем

заказа

обоих

случаях

один

и тот

же. При этом элемент неопределенности учитывается в

резервном запасе.

Точка очередного заказа вычисляется следующим об-

разом:

= d

L + za

(15.5)

где

— точка очередного заказа (в единицах);

— средняя дневная потребность;

— период выполнения заказа в днях (период

между

моментом размещения заказа и моментом получения из-

делий по этому заказу);

z — число стандартных отклонений для заданного

уровня обслуживания;

— стандартное отклонение спроса в течение перио-

да выполнения заказа.

Глава.

15.

Системы управления товарно-материальными запасами при независимом спросе

479

Число

единиц

текущего

запаса

)

•

Диапазон изменения потребности

Резервный

запас

-^Дефицит

Время

Рис. 15.6.

Диапазон

отклонений

потребности

модели

фиксированным

объемом

заказа

Член

Z&L

представляет собой величину резервного запа-

са. Обратите внимание: если резервный запас выражен по-

ложительной величиной, то размещение очередного заказа

должно проводиться раньше. Другими словами, Я без ре-

зервного запаса — это просто средняя потребность в тече-

ние

периода выполнения заказа. Если потребность в тече-

ние

периода выполнения заказа ожидалась, например, на

уровне 20 изделий, а вычисление величины резервного за-

паса дало значение 5, то очередной заказ

будет

размешен

раньше (когда останется 25 изделий). Чем больше резерв-

ный

запас, тем раньше размешается очередной заказ.

Вычисление d

, a

и z. Потребность в изделиях в течение

периода выполнения заказа на пополнение запаса в дейст-

вительности представляет собой оценку, или прогноз того,

что мы ожидаем. Она может выражаться одним числом

(если, например, время выполнения заказа составляет один

месяц,

соответствующую

потребность можно вычислить

как

потребность за весь прошлый год, поделенную на 12)

или

суммой ожидаемых потребностей в течение периода

выполнения

заказа (например, суммой дневных потребно-

стей на протяжении 30-дневного периода выполнения за-

каза).

Если рассматривать ситуацию с суммированием

дневных потребностей, то d может быть прогнозируемой

потребностью, использующей

любую

из моделей прогнози-

рования,

описанных в

главе

13. Если, например, для вы-

числения d использован 30-дневный период, то простое

среднее можно вычислить следующим образом:

и 30 '

где п — количество дней.

Стандартное отклонение дневной потребности:

(15.7)

Поскольку а

относится к одному дню, в

случае,

если

время выполнения заказа

охватывает

несколько дней,

можно воспользоваться статистической предпосылкой о

том, что стандартное отклонение ряда независимых собы-

тий равно корню квадратному из суммы дисперсий. Та-

ким

образом, в общем

случае

ег =

JOT+0%+...

+ о\-

-'-

Предположим, например, что вычисленное нами стан-

дартное отклонение потребности равно 10 изделиям в

день. Если время выполнения заказа в нашем

случае

со-

ставляет пять дней, то стандартное отклонение для пяти-

дневного периода

будет

таким (каждый день считается не-

зависимым

от

остальных):

V(10)

+(10)

(10)

22,36

Теперь нам нужно вычислить г. Мы делаем это, вы-

числяя E(z), т.е. дефицит изделий, который

удовлетворяет

заданному уровню обслуживания, а затем находя в

табл. 15.2

соответствующее

значение г.

Допустим, мы решили обеспечить уровень обслужива-

ния

Р (пусть, например, Р -

0,95.)

В этом

случае

на про-

тяжении

года

мы испытывали бы дефицит (1 - P)D изде-

лий,

или 0,05 Д где D — годовая потребность. Если бы

каждый раз мы заказывали Q изделий, то размещали бы

D/Q заказов в год. Табл. 15.2 основывается на выполне-

нии

условия a

= 1. Таким образом, любое E(z), взятое

нами

из таблицы, необходимо умножить на a

, если

*\. Ожидаемый дефицит изделий, приходящийся на

каждый заказ, таким образом, составит E(z)o

. Для одного

года

ожидаемый дефицит изделий составит E(z)a

x D/Q.

Таким

образом, мы имеем:

Процент

дефицита х Годовая потребность =

Дефицит изделий, приходящийся на один заказ х

х Число заказов за год.

Другими словами:

- Р) х D =

E(zJ(T

х D/Q.

После решения этого уравнения получим:

(15.9)

где

р_ требуемый уровень обслуживания (например,

удовлетворение 95%-ной потребности);

(!_/>)_

неудовлетворенная часть потребности;

— годовая потребность;

— стандартное отклонение потребности в течение

периода выполнения заказа;

Q — экономичный размер заказа, вычисляемый обыч-

J2DS

ным

способом (например, Q = J~jr~

E(z)

— ожидаемый дефицит изделий в каждом цикле

заказа, определяемый по табл. 15.2, при ст= 1.

480

Часть

IV.

Управление

снабжением

Обратите

внимание,

что в

формуле

(15.9)

годовая

по-

требность

отсутствует.

Это

связано

с тем, что E(z)

пред-

ставляет

собой

дефицит

изделий

каждом

цикле

заказа.

(В

году

D/Q

циклов

заказа.)

Сравним

два

примера.

Разница

между

ними

заключа-

ется

в том, что в

первом

примере

вариация

потребности

выражена

виде

стандартного

отклонения

на

протяжении

всего

цикла

выполнения

заказа,

в то

время

как во

втором

она

выражена

виде

стандартного

дневного

отклонения.

Пример

15.3.

Экономичный

размер

заказа

Пусть годовая потребность D=1000 единиц, экономичный

размер

заказа Q = 200 единиц, требуемый уровень обслужива-

ния Р = 0,95, стандартное отклонение потребности в течение

периода выполнения заказа ог = 25 единиц, в году 250 рабочих

дней,

а период выполнения заказа L - 15 дней. Требуется опре-

делить точку очередного заказа.

Решение

В нашем примере d

= 4 (1000 изделий в год, деленные на

250 рабочих

дней).

Воспользуемся формулой

R =

+ zo

= 4 х 15 + z х 25.

Чтобы

найти z, воспользуемся формулой (15.9) для E(z) и

найдем соответствующее значение в табл. 15.2. В нашем при-

мере Q =

200,

уровень обслуживания Р = 0,95, а стандартное

отклонение потребности в течение периода выполнения заказа

CTL

25. Следовательно,

£(z) =

О-0.95)200

0/|

Из табл. 15.2 по E(z) = 0,4 находим, что z = 0.

Подставляя

это значение в выражение для R, получаем

R = 4x15 + zx 25= 60 + 0 х 25 = 60 единиц.

Это говорит о

том,

что, когда текущий запас снижается до 60

единиц, нужно заказать еще 200 единиц.

Теперь вычислим потребность в изделиях, которая факти-

чески удовлетворяется в течение года. Это даст нам возмож-

ность увидеть, действительно ли получается 95%-ный уровень

обслуживания. E(z) — ожидаемый дефицит по каждому заказу

при

стандартном отклонении, равном 1. Дефицит по каждому

заказу в нашем

случае

составит

E(z)ai_

= 0,4 х 25 = 10. Посколь-

ку

каждый год размещаются пять заказов (1000/200), это озна-

чает

дефицит 50 единиц. Такой результат подтверждает, что

нам действительно удалось обеспечить 95%-ный уровень об-

служивания, поскольку из запаса можно получить 950 единиц

при

общей потребности в 1000 единиц.

Пример

15.4.

Величина

заказа и

точка

очередного

заказа

Ежедневная

потребность в определенном изделии имеет

нормальное распределение (среднее значение равно 60, а

стандартное отклонение — 7). Источник поставок считается на-

дежным и обеспечивает постоянное время выполнения зака-

за—

6 дней. Стоимость размещения заказа равняется $10, а

годовые издержки хранения составляют $0,50 на одно изделие.

Потерь, связанных с дефицитом изделий и невыполнением за-

казов,

нет. Допустим, что продажи осуществляются на протяже-

нии всего года. Определить величину заказа и точку повторного

заказа,

которые позволяли бы удовлетворить 95%-ную потреб-

ность из имеющегося запаса.

Решение

В нашем примере требуется вычислить величину заказа Q

а также точку повторного заказа R:

= 60;

$10;

Od=7; H=$0,50;

D = 60x365; L = 6.

Оптимальная

величина заказа будет

I2DS

12x60x365x10

0,50

936 изделий.

Чтобы

вычислить точку очередного заказа, нам нужно вы-

числить количество изделий, используемое в течение времени

выполнения заказа, и сложить его с резервным запасом.

Стандартное отклонение потребности в течение шести дней

(период

выполнения заказа) вычисляется на основе дисперсии

по отдельным дням. Поскольку потребность для каждого дня

является

независимой величиной ,

Дальше нам нужно знать, сколько требуется стандартных

отклонений для обеспечения указанного уровня обслуживания.

Как уже

было

показано,

Следовательно,

Как следует из табл. 15.2, для интерполяции E(z) =

2721

по-

лучаем

z =

-2,72.

Точка очередного заказа:

R =

L+

ZOL

= (60 х 6) +

(-2,72)

х 17,2 = 313,2 единиц.

Полученный

результат можно резюмировать следующим

образом:

заказ на 936 единиц размещается каждый раз, когда

количество изделий, остающееся в запасе, сокращается до 313.

Обратите внимание, что в этом

случае

резервный запас

ZOL

оказывается отрицательным. Это означает, что, если бы мы зака-

зывали вычисленное нами количество изделий Q =

936,

когда

уровень запаса снижается до ожидаемой потребности в течение

периода выполнения заказа (d

£. = 360), мы обеспечили бы более

высокий уровень обслуживания, чем нам требовалось.

Чтобы

снизить

его до 95%, нужно допустить больше нехваток,

выдавая

заказы в точке, расположенной несколько ниже вычисленной на-

ми

точки очередного заказа (313). Может, такой вывод покажется

вам странным, но это действительно так. В этом

случае

мы фак-

тически ожидаем дефицит изделий в каждом цикле заказа.

Мы можем проверить уровень обслуживания, обеспечивае-

мый в этом примере, указав, что нам пришлось бы размещать

23,4

заказов в год (60 х 365/936). В каждый из периодов нам

пришлось бы сталкиваться с дефицитом 46,8 единиц

(2,72 х 17,2). Таким образом, мы испытывали бы дефицит 1095

изделий в год (48,6 х 23,4). Следовательно, уровень обслужи-

вания составит, как нам и требовалось, 0,95 =

[(21 900

1095)/21 900].

Как уже

указывалось,

стандартное

отклонение

для

суммы

неза-

висимых

переменных

равняется

корню

квадратному

из

суммы

этих

переменных.