Czichos H., Saito T., Smith L.E. (Eds.) Handbook of Metrology and Testing

Подождите немного. Документ загружается.

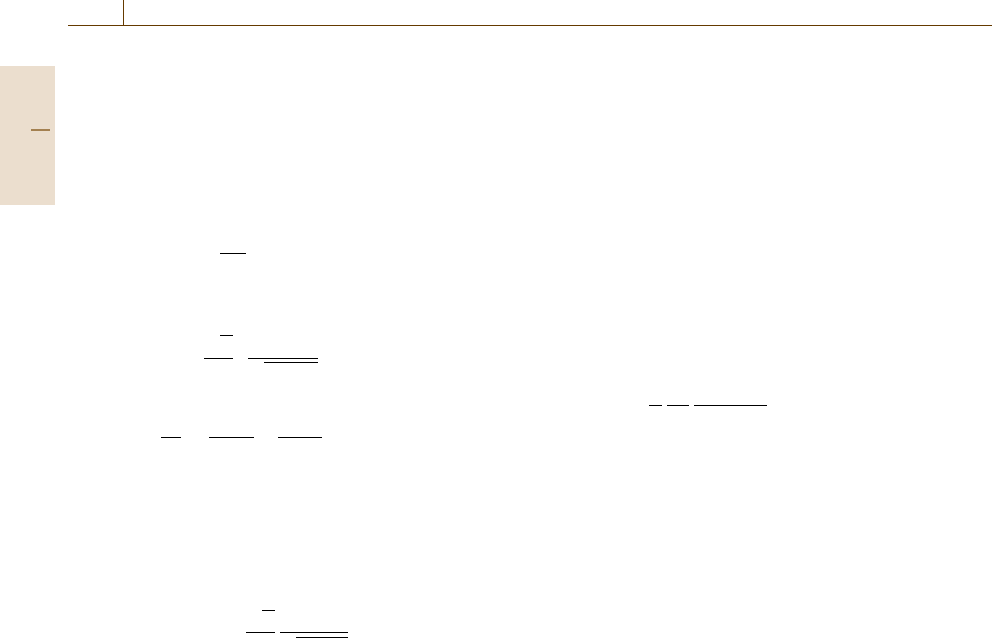
388 Part C Materials Properties Measurement

Principle. The total measured compliance C

is the sum

of contact compliance C

and the machine compliance

thus

, (7.35)

where C

is derived from the derivative of the (uncor-

rected) test force removal curve at maximum force





−1

(7.36)

and C

is the contact compliance of the specimen ma-

terial

√

)

(7.37)

with

1 −ν

(7.38)

and

= h

max

−ε F

max

, (7.39)

where E

and ν

are, respectively, the Young’s modulus

and the Poisson number of the indenter.

Thus the total compliance is

√



)

. (7.40)

If it can be assumed that the elastic modulus is con-

stant and independent of indentation depth, a plot of C

versus A

−1/2

is linear for a given material and the in-

tercept of the plot is a direct measure of the machine

load-frame compliance. The best values of C

are ob-

tained when the second term on the right-hand side

of (7.39) is small, i. e., for large indentations. In addi-

tion, the largest indentations are advantageous to ﬁnd

area function. A perfect modiﬁed Berkovich indenter,

for instance

A(h

) =24.5h

(7.41)

can be used to provide a ﬁrst estimate of the contact

area. Initial estimations of C

and E

are thus obtained

by plotting C

versus A

−1/2

for the two largest indenta-

tions in the reference block. Using these values, contact

areas are computed for all, at least six, indentation sizes

by rewriting (7.39)as

(C −C

)

, (7.42)

from which an initial guess at the area function is made

by ﬁtting A

versus h

data to the relationship

A(h

)

=24.5h

1/2

1/4

+···+C

1/128

, (7.43)

where C

–C

are constants. The lead term describes

a perfect modiﬁed Berkovich indenter; the others de-

scribe deviations from the Berkovich geometry due to

blunting of the tip.

The procedure is not complete at this stage because

the exact form of the area function inﬂuences the values

of C

and E

, so using the new area function the pro-

cedure shall be applied again and iterated several times

until convergence is achieved.

7.4 Strength

The strength of materials is inﬂuenced by the strain

rate, temperature, loading manner and chemical envi-

ronment. The conventional test for the examination of

the strength of materials is tension testing with a slow

strain rate of around 10

−3

−1

at room temperature.

Tensile properties obtained using this test are widely

used in engineering practices such as mechanical de-

sign, fabrication and maintenance of products. In the

case of brittle materials, compression or bending tests

are frequently used to examine their strength. These

tests are done under so-called quasistatic-loading con-

ditions. Tests at very slow strain rates are performed

to examine creep or stress–relaxation behavior. To con-

sider automobile collision, earthquakes etc., strength at

a high strain rate such as 10

−1

is required; impact

or high-speed deformation testing, such as a Hopkinson

pressure-bar test, is employed. Resistance to fracture

under cyclic loading is called fatigue strength. Strength

is also inﬂuenced by temperature as well as the envi-

ronment accompanied by chemical reactions such as

corrosion, or radiation damage. Fracture is frequently

found to occur under combined conditions of stress,

microstructural change and chemical reaction. In some

cases, high-temperature strength or low-temperature

toughness are of importance for engineering application

of materials, so that the meaning of the strength of ma-

terials is not unique but depends on the conditions of

their use.

Part C 7.4

Mechanical Properties 7.4 Strength 389

7.4.1 Quasistatic Loading

Strength

According to their loading speed, tests are classiﬁed

as quasistatic (or simply static) or dynamic. The most

common quasistatic measurement of the strength of ma-

terials is tension testing. The strength of a material has

three different meanings, which it is important not to

confuse. First, when the applied load is small, defor-

mation is reversible, that is, elastic deformation occurs.

Stresses are proportional to elastic strains and the so-

called Hooke’s law holds. The slope between tensile

stress and tensile elastic strain is called the Young’s

modulus, as was explain in Sect. 7.1. A material with

high Young’s modulus is strong, or rigid to elastic de-

formation. Secondly, when the applied stress becomes

higher, materials usually show plastic deformation. The

stress at the onset of plastic ﬂow is called the yield

strength, which has no direct relation with the Young’s

modulus. The yield strength indicates resistance against

plastic ﬂow. In the case of engineering materials, it is

necessary to deﬁne how to determine the yield strength

for mechanical design. Usually, 0.2% proof stress or

lower yield strength is employed. Thirdly, materials

show fracture under applied stress. Since there are many

fracture mechanisms, the strength against fracture is dif-

ferent from the yield strength. Ductile materials show

workhardening with plastic deformation and plastic in-

stability, i. e., necking in the case of tension, resulting in

dimple fracture. Frequently fracture occurs after a con-

siderable amount of plastic ﬂow, but fracture takes place

with little or no plastic deformation. This is called brit-

tle fracture, so that the resistance to brittle fracture is

another aspect of strength. Fracture is also strongly de-

pendent on the chemical environment.

Tension Test

This test is usually performed at room temperature with

a strain rate of 10

−4

–10

−1

. The testing procedure

and the shape and dimensions of a tensile specimen

should be taken from the ISO or other related standards,

depending on the materials and products under consid-

eration. The loading speed, or extending speed, should

be controlled within the above strain-rate range us-

ing a gear-driven type or servo-hydrostatic-type tester.

During testing, the applied load and displacement of

a gage length of a tensile specimen should be recorded.

Then, the load–displacement diagram can be obtained.

The curve is converted to a nominal stress–strain curve

and sometimes further to a true stress–strain curve.

Typical tensile properties such as the yield strength,

tensile strength, uniform elongation, total elongation,

workhardening exponent (n-value), r-value etc., can be

obtained from the results of the tension test.

Stress–Strain Curves of Ductile Materials

An example of the standard tension specimens is shown

in Fig. 7.37. Depending on the purpose, a strain gage or

extensometer is attached to monitor the change in gage

length (ΔL), while the load (F) is measured simultane-

ously with a load cell. Based on the initial area (A

)and

gage length (L

), the nominal stress (σ ) and nominal

strain (ε) are obtained by the following equations

σ = F/A

, (7.44)

ε =ΔL/L

. (7.45)

Here, the units for F and ε are Pa (= N/m

)andm/m

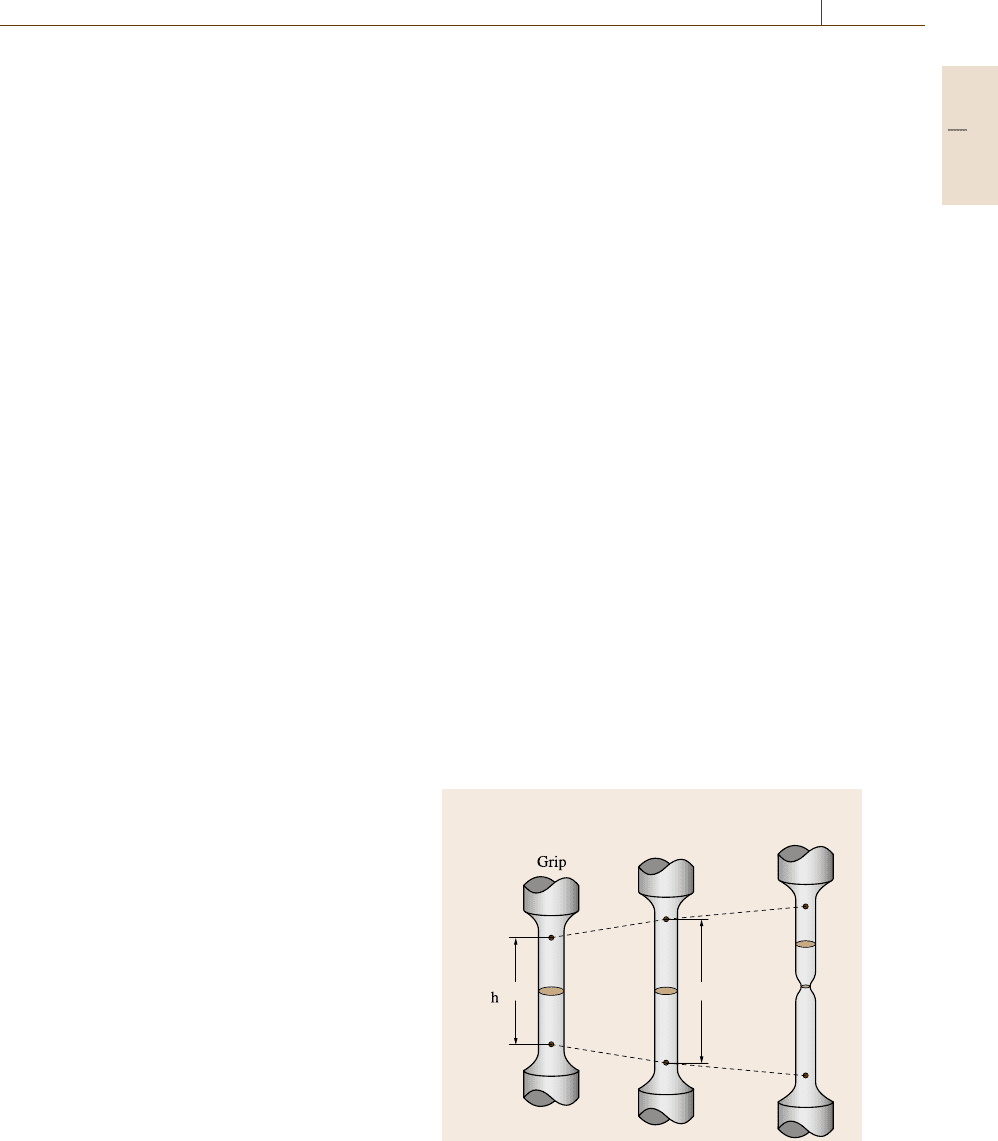
(nondimensional), respectively. In Fig. 7.38, two typical

examples of nominal stress–strain curves are presented;

one shows the case of discontinuous yielding (a) and

the other shows continuous yielding (b). Most metals

and alloys show the type of yielding shown in (b). How-

ever, annealed mild steels, which are widely used, show

the type shown in (a). As can be seen, these curves are

divided into three regions.

1. A linear elastic region at the beginning, where stress

is proportional to strain and the deformation is re-

versible.

2. After the onset of plastic ﬂow, the curve devi-

ates from the elastic line. The ﬂow stress increases

with increasing strain, meaning that the material is

strengthened by plastic deformation; this is called

Before test

Gauge

length

Uniform

deformation

Local

deformation

ALNecking

Grip

a) b) c)

Fig. 7.37a–c Tension specimen and macroscopic tensile

deformation behavior

Part C 7.4

390 Part C Materials Properties Measurement

Nominal stress

Nominal strain

Elastic line

Luders band

Uniform elongation

Local

elongation

0.2

0.2%

Fig. 7.38a,b Nominal stress–strain curves: (a) discontinu-

ous yielding and (b) continuous yielding

workhardening. When unloaded, only the elastic

strain is recovered but a permanent deformation,

i. e., plastic strain, remains. In this region, uni-

form plastic deformation occurs. For plastic strains,

the condition of constant volume is often assumed

(Fig. 7.37b[7.206]).

3. After reaching the maximum stress, which is called

the ultimate tensile strength (UTS) or simply the

tensile strength (TS), a lower stress is enough to

a) b) c)

20 µm 200 µm 200 µm

Fig. 7.39a–c Fracture surface:

(a) dimple, (b) cleavage and

continue to deform the material plastically because

necking occurs (Fig. 7.37c). After the onset of neck-

ing, deformation is localized to a necked region in

which the stress condition is no longer uniaxial but

is triaxial. Microvoids form inside the necked re-

gion, grow, connect to each other and lead to slip-off

of the remaining, outside ring region. Thus, the view

after fracture looks like a cup and a cone and hence

is called cup-and-cone fracture. This phenomenon

is typical of ductile fracture. The inner, ﬂat area con-

sists of dimples; the dimple pattern observed on the

fracture surface is shown in Fig. 7.39a.

4. When a material is brittle, as is the case for ce-

ramics, necking is not observed and the ﬂow curve

stops suddenly at the fracture stress, often within

the elastic regime. In such a case, the fracture sur-

face consists of cleavage or transgranular facets.

Examples of the fracture surface are presented in

Fig. 7.39band7.39c,

True Stress–Strain Curves

and the Workhardening Exponent (n-Value)

Within the uniformly elongated regime in Fig. 7.38,the

assumption of constant volume for plastic strains holds

approximately. This means that the cross section in the

gage volume in Fig. 7.37 decreases with increasing ten-

sile strain. Hence, the area (A) to support the applied

stress decreases with deformation so that the stress per

unit area is given by

∗

= F/A (7.46)

instead of (7.44); σ

∗

is called the true stress. Similarly

to σ

∗

, the gage length l

changes continuously with

deformation. Then, the true strain (ε

∗

)isdeﬁnedby

∗



dl/l =ln(l/l

) . (7.47)

One of the merits of using ε

∗

is its additive nature.

For instance, when a length changes from L

to L

Part C 7.4

Mechanical Properties 7.4 Strength 391

Fig. 7.40 Stress condition in a necked region in tension

test

and then to L

, the true strain from L

to L

ln(L

) and from L

to L

is ln(L

). There-

fore, ln(L

) +ln(L

) = ln(L

) holds. In

contrast, in the case of nominal strain, we have (L

−

)/L

+(L

−L

)/L

=(L

−L

)/L

, and hence

this property is not additive. Taking the assumption of

constant volume (A

= AL) we obtain the following

conversion from nominal stress and strain to true stress

and strain. Thus, we ﬁnd the relation for true stress

versus true strain starting from Fig. 7.38 by using

∗

= F/A

=σ(1 +ε) , (7.48)

∗

=ln(L/L

) =ln(1 +ε) . (7.49)

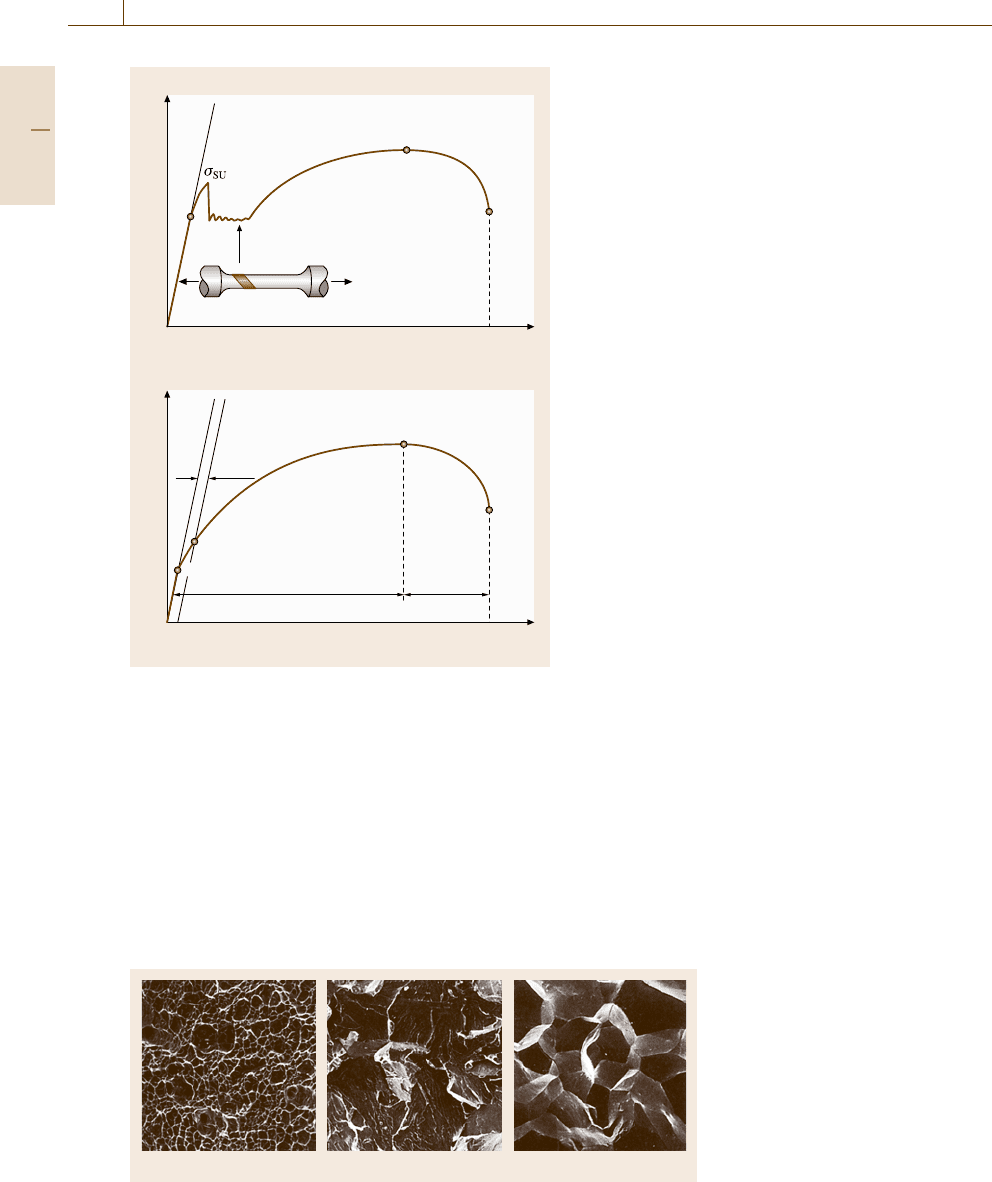
After the onset of necking, the specimen geometry

changes and the stress condition is also altered. As

showninFig.7.37c and Fig. 7.40, the stress condition

in a necked region is not uniform but is a compli-

cated triaxial stress condition. According to Bridgman’s

analysis [7.207], the tensile stress at the surface of the

smallest cross section, σ

(Fig. 7.40), is given by

F/ A

(1 +2R/a)ln(1+a/2R)

, (7.50)

where R and a are given in Fig. 7.40. Microvoids form

in the center of the necked region under triaxial stresses,

as explained above, leading to cup-and-cone fracture.

An example of curves of true stress versus true strain

converted from the nominal stress–strain curve by us-

ing (7.49)and(7.50) is shown in Fig. 7.41. This shows

that workhardening continues even in local deforma-

Nominal stress/true stress (MPa)

Nominal strain/true strain

1200

1000

800

600

400

200

0 0.1 0.2 0.3 0.4

True stress/

true strain

Nominal stress/

nominal strain

Work

hardening

rate

Fig. 7.41 True stress–strain curve in which the workhard-

ening rate is plotted to indicate the onset of necking

tion; the necking is caused from the balance between

cross-sectional area reduction and workhardening with

increasing tensile plastic strain. Hence, the crossing

point of the true stress σ

∗

and the workhardening rate

dσ

∗

/dε

∗

shows the onset of necking (Fig. 7.41).

Tensile Properties

Tension testing is simple and gives us lots of useful in-

formation on mechanical properties. So, this test is the

most basic and popular to understand the mechanical

behavior of materials. Several parameters for engineer-

ing use obtained by tension testing are explained below.

Elastic Limit and Proportional Limit

Most mechanical products are designed to be used

within the regime of elastic deformation. The rigor-

ous limit of elastic deformation is determined by the

elastic limit or proportional limit on the stress–strain

curve. The proportional limit is the point of deviation

from the linear relationship between stress and strain.

On the other hand, the elastic limit is found as the max-

imum stress without permanent strain after unloading.

These stresses are very sensitive to the method used to

measure strain. Within the linear stress–strain regime,

as was explained in details in Sect. 7.1, the Young’s

modulus (E) is determined from the slope, while the

Poisson’s ratio (ν) is determined by the absolute ratio

between the transverse strain and tensile strain. When

the tensile direction is taken as the x

-axis, these are

determined by

E = σ

/ε

, (7.51)

ν =

/ε

(7.52)

Part C 7.4

392 Part C Materials Properties Measurement

In the case of steel, E is nearly 200 GPa and ν is ap-

proximately 0.3. The elastic strain in steels is usually

less than 1%, which is very small compared with the

uniform elongation of the order of 10%. We note here

that the constant-volume assumption is not applicable

to elastic deformation.

Yield Strength

Special measurements such as those based on strain

gages are required for the measurement of elastic strains

less than 0.01 so that the yield strength (YS)isde-

termined for mechanical design using the conventional

tensile test. In the case of discontinuous yielding ob-

served in mild steel, as shown in Fig. 7.38a, the upper or

lower yield point is observed on the stress–strain curve

and used as the yield strength in engineering. After the

upper yield point, a plastic-deformation regime called

the Luders band appears and spreads within the speci-

men gage volume under the lower yield stress. Since the

upper yield strength is strongly dependent on the ten-

sile speed, i. e., the strain rate, the lower yield strength

is more popularly used. The strain during this hetero-

geneous deformation is called the Luders elongation,

which is also dependent on grain size.

On the other hand, Fig. 7.38b shows the case of

continuous yielding, which is observed in many met-

als and alloys such as aluminum, austenitic stainless

steel etc. 0.2% proof stress is usually employed, which

means a plastic (permanent) strain of 0.2% remains af-

ter unloading. Usually the elastic linear line is shifted by

0.2% and the intersection with the stress–strain curve is

found. Macroscopic yielding can be observed to take

place at this point. Although 0.2% strain is the choice

for engineering, other strains, for instance 0.1%, are

employed in other industrial ﬁelds.

Tensile Strength

The maximum stress appearing in Fig. 7.38 is deter-

mined by the tensile strength (TS), frequently called the

ultimate tensile strength (UTS). In the case of an ex-

treme design that allows plastic ﬂow, TS is employed as

the design strength.

Ductility

Parameters to describe the ductility includes uniform

elongation, total elongation and reduction in area af-

ter fracture. Uniform elongation is important for plastic

forming etc. and is determined as the strain at the tensile

strength. After the tensile strength, local deformation,

i. e. necking, starts. The total strain is given as the strain

to fracture in Fig. 7.41. It should be noted that the to-

tal elongation is dependent on the gage length adopted.

Therefore, fracture strain (ε

) is sometimes used, which

is deﬁned as ln(A

), where A

refers to the smallest

area in the necked region after fracture. Conventionally,

the reduction in area (ϕ)deﬁnedby[(A

− A

)/A

]×

100% is used. The extreme case observed in a pure

metal is a point fracture, where A

=0.

Workhardening Exponent (n-Value)

The true stress–strain curve shown in Fig. 7.41 is often

ﬁtted by using the following Hollomon’s equation

∗

= K(ε

∗

)

, (7.53)

where K and n stand for the strengthening factor

and the workhardening exponent (n-value), respec-

tively. By taking two measuring points or by using

the least-squares method for ln σ

∗

versus ln ε

∗

within

an appropriate strain regime, these K and n values

are determined. The n-value is important because it is

equivalent with uniform elongation. The plastic insta-

bility condition, i. e., the onset of necking can be given

dF = σ

∗

dA + A dσ

∗

=0 , (7.54)

where F is the applied tensile load. This equation

is rewritten by σ

∗

= dσ

∗

/dε

∗

under the assumption

of constant volume and therefore ε

∗

= n is obtained.

Alargen-value means excellent plastic formability.

Rankford Value (Plastic Anisotropy: r-Value)

Another parameter that indicates the plastic formability,

and which is also obtained by the tension test for sheet

metals and alloys, is the r-value. When tensile strain

reaches 10–20%, the strain for a thickness of ε

and the

strain for a width of ε

are measured and the r-value is

determined by

r =ε

/ε

. (7.55)

If the assumption of constant volume is used, this be-

comes

r =ln(W

/W)/ ln(LW/L

) , (7.56)

where W

, L

and W, L refer to the width and gage

length in the tensile direction before and after the ten-

sion test, respectively. These values are much more eas-

ily measured precisely than the thickness because most

cases use thin sheets. In an isotropic material, the r-value

equals unity. Commercially available materials gener-

ally show anisotropic feature in plastic ﬂow because of

their texture. Materials with high r-values are desirable

Part C 7.4

Mechanical Properties 7.4 Strength 393

for heavy drawing because the thickness change is small.

To achieve this, texture control is important.

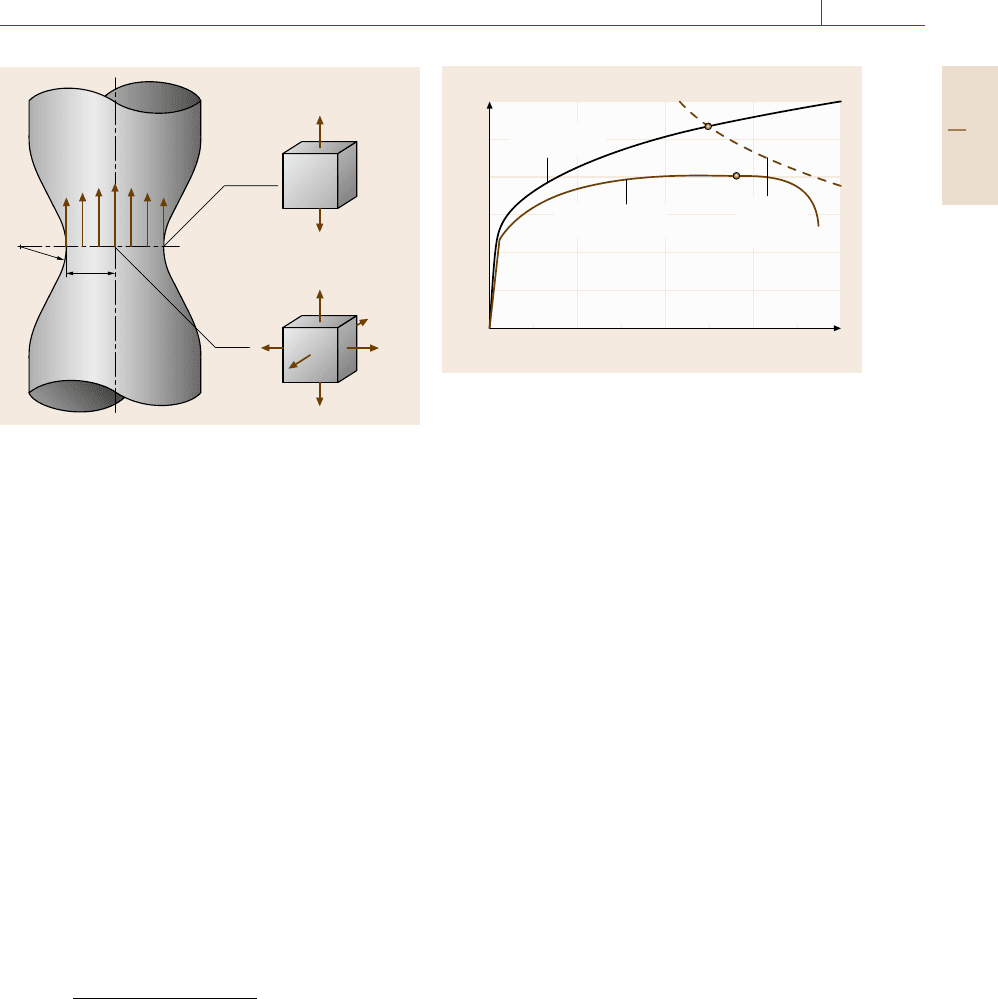
The Compression Test

The compression test looks like the reverse of the ten-

sion test, but more skill is required to obtain reliable

stress–strain curves. A schematic illustration of com-

pression of a round column is presented in Fig. 7.42,

where the top and bottom surfaces of the specimen

should be maintained with good parallelism. Friction

between the specimen and the anvil must be mini-

mized using an appropriate lubricant such as graphite or

S powder otherwise bulging, shown in Fig. 7.42b,

becomes serious and leads to constrained deformation.

If the compression alignmanet is not satisfactory with

respect to the specimen axis, buckling or bending oc-

curs easily at small strains. To avoid such buckling,

the length of the specimen should be designed taking

a) b)

σσ

Fig. 7.42a,b Compression test where bulging is illustrated

Nominal stress/true stress

Nominal strain/true strain

True stress/

true strain

Nominal stress/

nominal strain (compression)

Nominal stress/

normal strain (tension)

Fig. 7.43 Compression ﬂow curve compared with that in

tension

the cross-sectional area into consideration. Usually, the

ratio of the diameter of the cross-sectional area d

the length h

is chosen as 1.0–3.0. When the top and

bottom of a specimen are plastically constrained by an

anvil, the stress distribution within the cross section is

not uniform and plastic deformation occurs in an inho-

mogeneous manner within the specimen.

The nominal stress–strain curve obtained by the

compression test is higher than that obtained by the

tension test because the cross-sectional area increases

with deformation. Hence, ﬂow curves measured by the

tension test and the compression test should be com-

pared in terms of true stress–strain curves. If a material

shows isotropic plastic deformation, these two ﬂow

curves (the true stress–strain curves) coincide, as shown

in Fig. 7.43. However, if a material contains phase

or intergranular residual stress, so-called second-type

residual stresses, the yield strength will differ between

compression and tension, which is called the strength

difference (SD) effect. The SD effect is also caused

by crystallographic features in plastic ﬂow or stress-

induced martensitic transformations.

In general, the ﬂow stress (true stress) in compres-

sion after some amount of tensile plastic deformation

is smaller than that for continuous tension, as shown

in Fig. 7.44. This is called the Bauschinger effect (BE).

As seen in Fig. 7.44, the magnitude of the BE is of-

ten expressed by the BE stress or BE strain (Fig. 7.44).

Generally speaking, the ﬂow stress becomes smaller

when the strain path changes, even under biaxial or

triaxial stresses. In a stress space (the general stress

condition is described by six components, as will be

described later), the yield condition is shown using

True stress (MPa)

600

300

–300

–600

0 0.005 0.01 0.015 0.02

True strain

Tension

Tension Redrawing

Compression

0.001

0.5σ

0.5

Fig. 7.44 Tension-compression test to examine the Bau-

schinger effect (BE) in which the parameters of BE stress

(σ

−σ

)andBE strain β

0.5

are deﬁned

Part C 7.4

394 Part C Materials Properties Measurement

a) b)

Brinell test

Cross section

of specimen

Cross section

of specimen

Vickers test

Specimen surface

Fig. 7.45a,b Hardness tests by indenting deformation

the yielding surface. When a material is plastically

deformed and thus workhardened, the yielding stress

surface expands and moves in the stress space. Hence,

the yield strength after plastic deformation depends on

the loading conditions. Typical cases are: (1) isotropic

hardening, where the yield surface expands homoge-

neously, and (2) kinematic hardening, where the surface

moves without changing its shape and size. The BE is

important in order to understand plastic forming, which

is used to make mechanical parts. In addition, the BE

behavior is closely related to low-cycle fatigue behavior.

In the case of brittle materials such as concrete, in which

the SD effect for fracture is remarkable, the compressive

fracture strength is much higher than the tensile value.

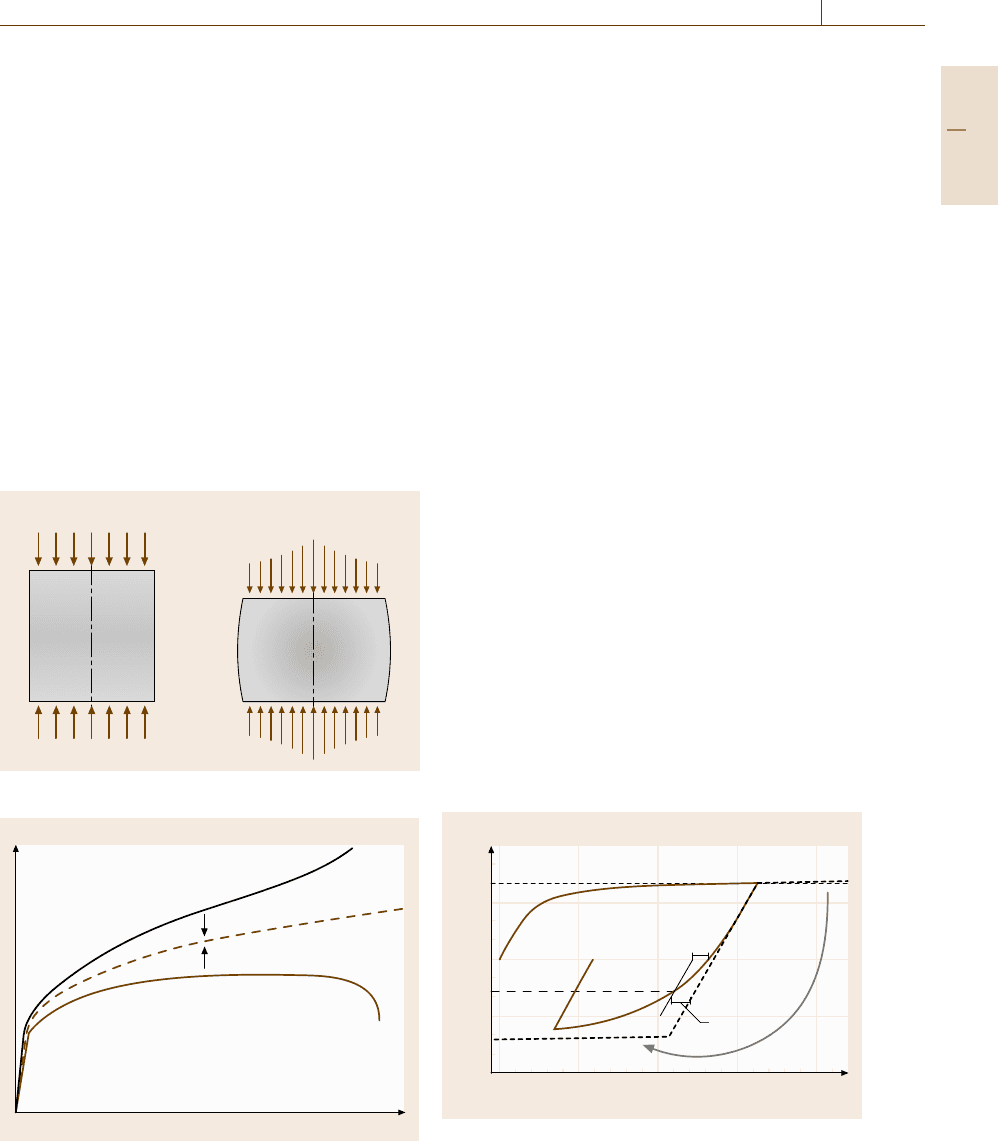
Hardness Test and Strength/Hardness Relations

In addition to the treatment of hardness measurements

methods given in Sect. 7.3, relations between strength

b)Tensile

strength

(GPa)

Rockwell

hardness

Brinell

hardness

Vickers

hardness

HRB

HRC

Vickers hardness HV 0.2 % proof stress (GPa)

21.61.20.80.40

100

0 200 400 600 800 1000

200

400

600

800

1000

1.5

0.5

100

200

300

400

500

600

Fig. 7.46a,b Relationship between hardness and tensile properties

and hardness are brieﬂy considered. The most popu-

lar measurement is a kind of compression test with

an indenter. The indenter is made from a hard mater-

ial such as diamond or high-carbon martensite steel.

As explained above and shown again in Fig. 7.45 an

indenter is pressed on the surface of a testing mater-

ial, and the indentation after unloading is measured.

Since the Vickers hardness test employs a pyramidal

diamond indenter, the applied stress is almost pro-

portional to the area, which means that the Vickers

hardness number is insensitive to the applied load.

As is estimated in Fig. 7.45, the deformation zone is

limited to just underneath of the indenter and is com-

plicated. According to an elasto–plastic analysis, the

representative plastic strain in the plastic zone is about

8%, so that the hardness number should correspond to

8% ﬂow stress in the simple tension or compression

test [7.208, 209]. Figure 7.46 shows the relationship

between the hardness and tensile properties, the yield

strength or tensile strength (8% proof stress is usually

not recorded). Excellent correspondence is found be-

tween the yield or tensile strength and hardness. The

experimental relationship of (7.57) is used to connect

the Vickers hardness number (HV) to the yield or tensile

strength (Y)

HV =cY , (7.57)

where the coefﬁcient c is 2.9–3.0. Therefore, the hard-

ness test is a convenient way to check the strength of

materials, particularly for engineering products.

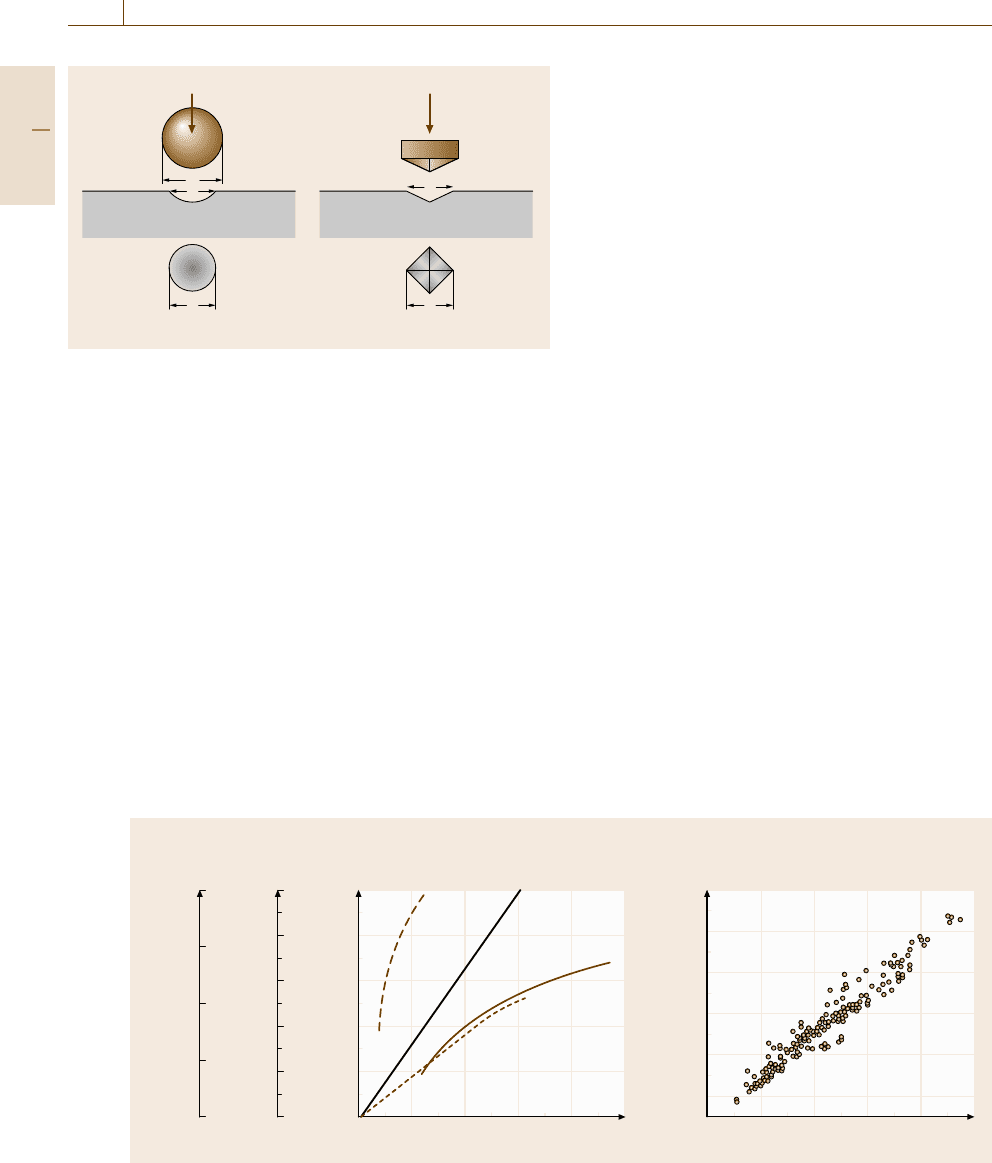
Supplementing the discussion of nanohardness

measurements given in Sect. 7.3.4, strengthening mech-

anisms will be considered brieﬂy. In most cases, the

Part C 7.4

Mechanical Properties 7.4 Strength 395

Vickers hardness HV

500

400

300

200

100

–2

–1

Square root of contact area (μm

1/2

)

Base hardness

Dislocations hardening

Precipitation hardening

Conventional test

Micro test

Ultra-micro test

Grain (block) size

hardening

Lath

Packet

Block

Fig. 7.47a,b Hardness with various loads to examine the

strengthening mechanism in a tempered martensite steel

shape of a diamond indenter is triangle pyramid because

the tip of square pyramid is difﬁcult to make precisely.

The test is performed under very small loads, such as

a few grams, and is widely used for thin-ﬁlm or elec-

tronics devices. One of the recent application [7.210]is

summarized in Fig. 7.47, where the hardness was meas-

ured using a wide range of applied loads for a tempered

martensite steel. Because an engineering material shows

multiscale heterogeneous microstructure that brings the

multiscaled heterogeneous plastic deformation. For ex-

ample, the tempered martensite is composed of laths,

blocks and packets as shown in Fig. 7.47a and hence

the strengthening mechanisms due to grain reﬁnement,

dislocation density, carbon solid solution and carbide

precipitation overlap. By examining the hardness with

various loads, using three kinds of hardness testers, the

contribution of individual strengthening mechanism can

be found separately, as illustrated in Fig. 7.47b.

The Bending Test

Schematic illustration of the bending test is presented

in Fig. 7.48. This test is frequently used to measure the

a) b)

Fig. 7.48a–c Bending test: (a) deformation aspect, (b) stress dis-

tribution in elastic deformation and (c) that in elasto–plastic

deformation

strength of brittle materials or the bending formability

of ductile materials. As shown in Fig. 7.48, two kinds

of tests, three- and four-point bending are used. three-

point bending is easy to carry out. However, four-point

bending is preferable because the bending moment M is

then constant in the central part of the specimen. When

a rectangular specimen is bent, as shown in Fig. 7.48a,

strain and stress distribution occurs in the cross sec-

tion, where the upper surface is in compression and

the lower surface is under tension. There exists a neu-

tral stress-free plane, which is denoted by the x-axis. If

the curvature is expressed by ρ, the normal strain under

elastic deformation is given by

ε = y/ρ . (7.58)

The normal stress is proportional to the strain, and

hence we obtain the maximum stress by

σ =6M/(bh

) , (7.59)

where b and h refer to the width and thickness of the

specimen, respectively. The stress distribution is shown

in Fig. 7.48b.

After yielding at M = σ

/6, the stress distribu-

tion changes from Fig. 7.48b–c, where σ

stands for the

yield strength. When M is further increased, the bound-

ary between the elastic region and the elasto–plastic

region moves towards the neutral plane. The stress or

strain distribution in the plastic region is dependent on

the workhardening of a material. A schematic illustra-

tion is given in Fig. 7.48c. When the applied moment

is removed, the residual stress distribution remains: ten-

sile stress at the upper surface and compression at the

bottom surface.

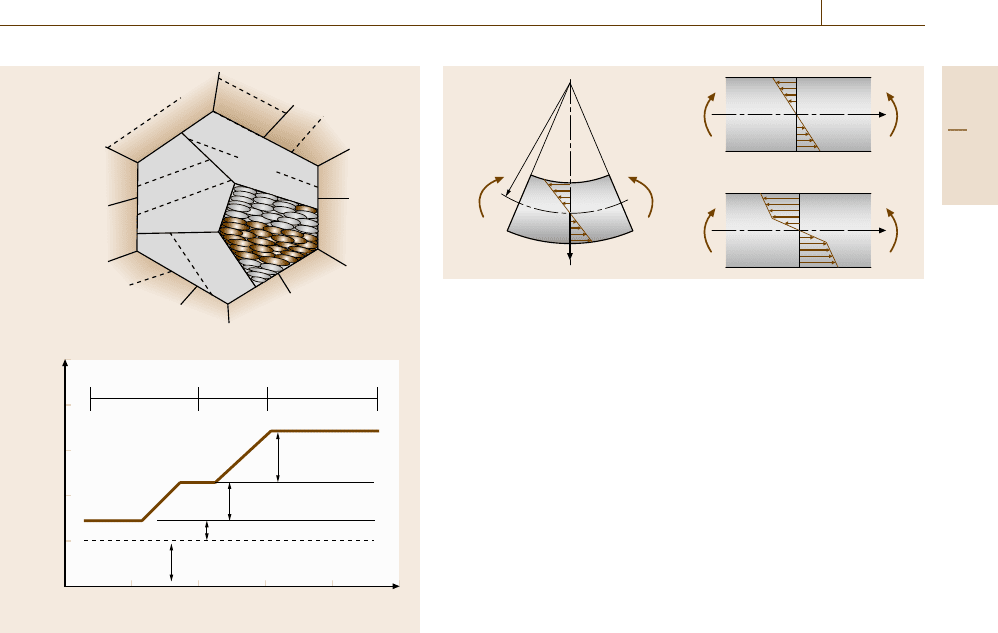
The Torsion Test

Shear deformation is related to the combination of bi-

axial deformation of tension and compression. This

Part C 7.4

396 Part C Materials Properties Measurement

Fig. 7.49a–c Torsion test: (a) deformation aspect, (b) stress dis-

tribution in elastic deformation and (c) that in elasto–plastic

deformation

conversion is achieved by rotating the coordinate sys-

tem by 45

◦

. In particular, the torsion test is used for

wires and bars. Figure 7.49 shows a schematic illustra-

tion of torsion (a) and the shear stress distribution (b) in

the cross section of a round bar with radius r. The engi-

neering shear strain γ is related to the shearing angle θ

and the bar length L by

γ =rθ/L . (7.60)

Considering the stress equilibrium, the torsion moment

(for torque T )isgivenby

τ =16T/πd

, (7.61)

where d refers to the diameter of the round bar speci-

men. Similarly to the bending test depicted in Fig. 7.48,

the stress distribution changes after yielding, as rep-

resented in Fig. 7.49c. Fracture usually takes place

perpendicularly to the specimen axis in ductile frac-

ture while along 45

◦

direction in case of brittle fraction.

In some cases, fracture along the longitudinal direc-

tion occurs, which is called delamination. Delamination

fracture has to be avoided for practical application of

wires.

Yielding Criteria under Multiaxial Stresses

Tension and compression tests are performed with uni-

axial loading. The general stress condition is a triaxial

stress, which is described by six components

⎛

⎜

⎝

⎞

⎟

⎠

When a special coordinate related to the principal

stresses, σ

(σ

,σ

) is employed, the shear stress

components all become zero. For instance, in the case of

the tension test along the tensile direction of the x

-axis,

the six stress components or three principal stresses are

written as

=σ

,σ

=σ

=0 ,σ

= σ

=0 ,

=τ

=0 . (7.62)

The yield strength σ

is the determined by σ

at 0.2%

plastic strain, or the Luders deformation. In the case of

the general stress condition, the stresses are converted

to principal stresses by changing the coordinate system.

For example, in the torsion test, τ =16T/πd

and the

other stresses are zero at the surface of a bar speci-

men from (7.61). Rotating the coordinate by 45

◦

gives

=−σ

=16T/πd

and the other stress components

are zero.

Two of the most popular criteria for yielding un-

der general stress conditions are the Tresca and von

Mises criteria. The Tresca criterion is based on the

maximum shear stress theory. When σ

>σ

,the

maximum shear stress is given by



−σ



/2. There-

fore, the yielding criterion is written by

−σ

=2k , (7.63)

where k is a constant and is given by σ

/2 for the tension

test.

On the other hand, the von Mises criterion is based

on the theory of shear strain energy. The shear strain

energy per unit volume is given by

1 +ν



(σ

−σ

)

+(σ

−σ

)

+(σ

−σ

)



Using the results of the tension test, the criterion can be

written as



(σ

−σ

)

+(σ

−σ

)

+(σ

−σ

)



=2σ

(7.64)

In general, yielding is found to occur at a stress con-

dition between these two criteria. Hence, the general

stress condition is projected to the case of the tension

test and the equivalent stress is then determined. For

instance, in the case of the von Mises criterion, the

equivalent stress σ

is given by



(σ

−σ

)

+(σ

−σ

)

+(σ

−σ

)



1/2

or more generally,



(σ

−σ

)

+(σ

−σ

)

+(σ

−σ

)



+σ



1/2

. (7.65)

Another interpretation of the von Mises criterion is the

maximum shear stress acting on the pyramidal plane in

the principal stress space.

Part C 7.4

Mechanical Properties 7.4 Strength 397

Torsion τ/σ

Tension σ/σ

von Mises

Tresca

0.8

0.6

0.4

0.2

0 0.2 0.4 0.6 0.8 1

Maximum stress

Fig. 7.50 Yielding under combined tension and torsion

stresses

A schematic illustration of the yielding surface un-

der combined torsion and tension loads [7.211, 212]

is shown in Fig. 7.50. Such a yielding condition un-

der general stress conditions is given by the yielding

surface in the stress space (six-dimensional or prin-

cipal stress space (three dimension)), which changes

with plastic deformation. This is called workhardening,

which includes isotropic hardening and kinematic hard-

ening. The Baushinger effect in Fig. 7.44 is an example

of kinematic workhardening, as already mentioned.

The Creep Test

Plastic deformation and fracture usually show time

dependence. When an external load is kept constant,

a specimen deforms plastically gradually, which is

called creep deformation. This is clearly observed at

high temperatures (T > 0.3T

), where T

denotes the

melting temperature of a material. In general, creep de-

formation at constant temperature is divided into three

stages in the creep curve, as shown in Fig. 7.51.

Here, after the initial strain that occurs during load-

ing to a certain ﬁxed stress, plastic strain initially

increases gradually, which is called transient creep. The

rate of increase of the strain in transient creep satu-

rates to a constant rate in the second regime. This is

called steady creep. The third regime, called tertiary

or accelerated creep, leads to the rupture of the spec-

imen. This effect is important, but it is not clear why

and when this acceleration from steady to tertiary creep

takes place. When the external load is small, tertiary

Elongation

Transient

creep

Accelerated

creep

Initial strain

Steady creep

Fracture

Holding time

Fig. 7.51 General creep deformation behavior under con-

stant load and temperature

creep is not observed and hence the specimen does not

fracture.

The experimental methods to examine creep behav-

ior include the constant-stress creep test, the torsion

creep test, the tension-torsion combined test, cyclic

loading creep, and the creep crack-propagation test.

A tester with an electric furnace and a lever-type load-

ing system for a round bar specimen is popular. In

general, creep rupture requires a long time, so that

many testers are used simultaneously. A dial gage

or differential transducer with a high sensitivity is

also required for strain measurement. When the ex-

perimental data obtained at various temperatures are

summarized by employing the following Larson–Miller

parameter,

λ = T(20 +log t

)×10

−3

, (7.66)

where t

stands for the rupture time, the experimen-

tal data for applied stress (σ) versus t

are well sum-

marized by a σ –λ master curve. The master curve

is inﬂuenced by strengthening mechanisms such as

solid solution hardening, grain reﬁnement, precipitation,

etc. The speed of crack growth is evaluated from the

viewpoint of fracture mechanics as will be explained

in Sect. 7.4.

Stress Relaxation

Plastic deformation shows time dependence, as ex-

plained for creep where the external stress is kept

constant. On the other hand, when a specimen is

pulled to induce plastic ﬂow and then kept at a con-

stant total strain, plastic ﬂow occurs with holding time

and hence stress (elastic strain) decreases, which is

called stress relaxation. To measure relaxation behavior,

Part C 7.4