Эськов В.Д., Каталевская А.В., Сипайлов А.Г. Теоретические основы электротехники. Часть 1
Подождите немного. Документ загружается.

131
Больше того, поскольку суммарный ток всех трех источников
120
/3
A
AAA
UU U U
равен нулю, то эти источники можно вообще
отключить, и режим остальной части цепи по-прежнему не изменится!
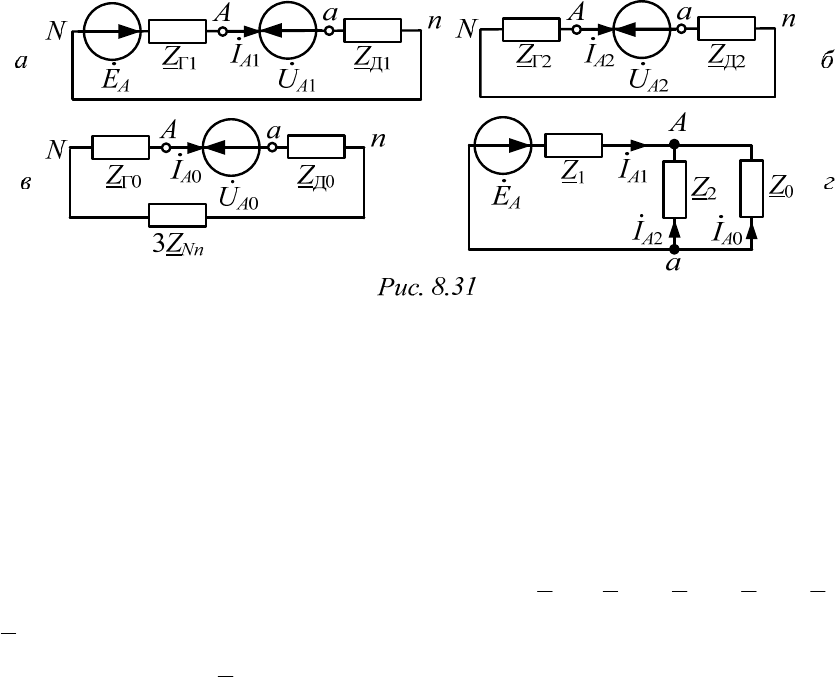
В результате получается расчетная схема, которая показана на
рис. 8.31, г. Формулы для определения составляющих токов и напряже-
ния на зажимах оборванного провода линии остаются теми же самыми.
В этом легко убедиться, рассчитав эту
схему, например, методом узло-
вых потенциалов.
Пример 8.4
Короткое замыкание одной фазы линии (А) на землю в системе ге-
нератор–двигатель, фазы которых соединены звездой, причем
нейтральная точка генератора заземлена (рис. 8.30, а).
Известны ЭДС генератора, образующие симметричную систему
прямой последовательности
2
,
A
BC
E
aE a E
сопротивления генера-
тора и двигателя всех последовательностей
Г1
,
Z
Г2
,Z
Г0
,
Z
Д1
,
Z
Д2
,Z
Д0
,Z включающие в себя сопротивления проводов линии, и сопротив-
ление заземления
З
.
Z
Определить ток короткого замыкания
К
.
I
Решение
1. Заменим несимметричный участок системой источников тока
,
A
I
,
B
I
,
C
I
на зажимах которых сохраняются напряжения ,
A
U
,
B
U
C
U
(рис. 8.32, б). Чтобы замена была эквивалентной, должны выпол-
няться условия несимметрии:
0,
A
U
0,
B
I
0.
C
I
В то же время
К
.
A
I
I

132
2. Разложим систему токов
,
A
I
,
B
I
C
I
на симметричные со-
ставляющие и применим принцип наложения. В подсхемах для каждой
последовательности существует симметричный режим, поэтому расчет
можно вести на одну фазу («особую» – в данном случае это опять фа-
за А). На рис. 8.33 показаны эти подсхемы. Обратим внимание, что ток
нулевой последовательности в фазах двигателя не течет, поскольку его
нейтральная точка не заземлена. В то же время в схему нулевой после-
довательности входит утроенное сопротивление заземления (по той же
причине, что и в предыдущем примере). Справедливым остается и заме-
чание по поводу ЭДС генератора.
3. Перепишем условия несимметрии применительно к составля-
ющим тока и напряжения особой фазы с учетом формул (8.1–8.4):
120 120К
0; / 3.
A
AA A AAA
UU U U I I I I
4. Найдем по закону Ома составляющие напряжения
A
U
на за-
жимах источников тока в подсхемах и, просуммировав их с учетом со-
отношения между составляющими тока
,
A
I
определим ток короткого
замыкания.
11
11 11111
22
222222
00
000
(/ ),где /( );
, где /( );
, где 3.
AA A
ГГДГД
AA
ГД Г Д
AA
ГЗ
UEZIZ ZZZZZ
UIZ ZZZZZ
UIZ ZZZ
Э
1 Г11 2 0 1 2 0
К
Э
1 Г1
Тогда 3/()3/(),
где /.
A
А
I
EZZZZZ EZZZ
EEZZ
Примечание. Составим и для этого режима расчетную схему за-
мещения. В схемах рис. 8.33, а–в по отношению к зажимам источников
тока заменим параллельные ветви одной эквивалентной. При этом в
каждой из подсхем будет протекать один и тот же ток
К
3.I
Поэтому
можно объединить эти подсхемы в один контур и каждая из них будет
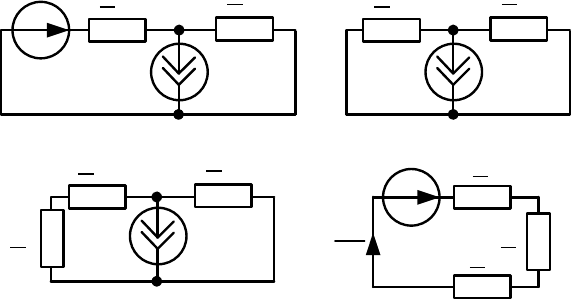
133
работать в прежнем режиме. Больше того, источники тока можно за-
мкнуть накоротко, а ток в контуре останется прежним, поскольку сум-
марное напряжение на этих источниках равно нулю. В результате полу-
чим расчетную схему, которая показана на рис. 8.33, г. Нетрудно убе-
диться, что формулы для определения тока короткого замыкания
К
I
и
симметричных составляющих напряжения
A
U
сохраняют свой вид.
Рис. 8.33
а б
в г
Z
Г2
n
N
Z
Д2
A
0
I
A2
.
U
A2
.
Z
Г0
n
N
Z
Д0
A
0
3Z
З
I
A0
.
U
A0
.
Z
1
Z
0
Z
2
N
U
A2
.
U
A1
.
U
A0
.
I
К
.
3
E
Э
.
Z
Г1
n
N
Z
Д1
A
0
I
A1
.
E
A
.
U
A1
.
8.14. Высшие гармоники в трехфазных цепях
Если в трехфазной цепи действует симметричная система несину-
соидальных ЭДС, то они сдвинуты по фазе на одну треть периода, т. е.
.3/3/ TteTtete
CBA
Рассмотрим гармонику порядка k во всех трех фазах этой системы,
учитывая, что
2.Tk k
Если
() sin ,
A
kkm k
etE kt
то
() sin 2 /3;
Bk km k
etE kt k
() sin 2 /3.
Ck km k
etE kt k
При
3,kn
где n – целое, окажется
2/32,kn
тогда
),()()( tetete
CkBkAk
то есть гармоники, кратные трем (3, 6, 9, …), образуют систему нулевой
последовательности.
При
31kn получим
2/32 2/3,kn
тогда
() ( 2 /3) ( 2 /3),
A
kBk Ck
etet et
то есть гармоники, чей порядок на единицу больше числа, кратного
трем (1, 4, 7, …), образуют систему прямой последовательности.
И очевидно, что при
32kn
окажется, что гармоники, чей номер
на единицу меньше числа, кратного трем (2, 5, 8, …), образуют систему
обратной последовательности:
134
() ( 2/3) ( 2/3).
A
kBk Ck
etet et
Иными словами, если из номера гармоники вычесть наибольшее
число, кратное трем, то остаток будет равен индексу последовательно-
сти, которую образуют три ЭДС этой гармоники: 0 – нулевая, 1 – пря-
мая, 2 – обратная. Так что даже при симметричной системе несинусои-
дальных ЭДС в цепи появляются группы напряжений и токов, которые
можно оценить как симметричные составляющие
различных последова-
тельностей. Поэтому расчет трехфазных цепей, в которых действуют
источники несинусоидальных напряжений и токов, следует вести мето-
дом наложения с учетом данного обстоятельства. Составляя для каждой
гармоники расчетную схему замещения, нужно не только определять ее
параметры в зависимости от частоты, но и выбирать конфигурацию од-
нофазной подсхемы, удовлетворяющую условиям существования
сим-
метричных составляющих соответствующей последовательности.
В большинстве практически важных случаев ЭДС генераторов не содер-
жат ни постоянной составляющей, ни четных гармоник, поэтому в дальней-
ших рассуждениях будем учитывать лишь нечетные гармоники (1, 3, 5, …).
Рассмотрим различные схемы соединения фаз в симметричной
трехфазной цепи, где действует симметричная система несинусоидаль-
ных ЭДС, обладающих симметрией относительно
оси абсцисс.
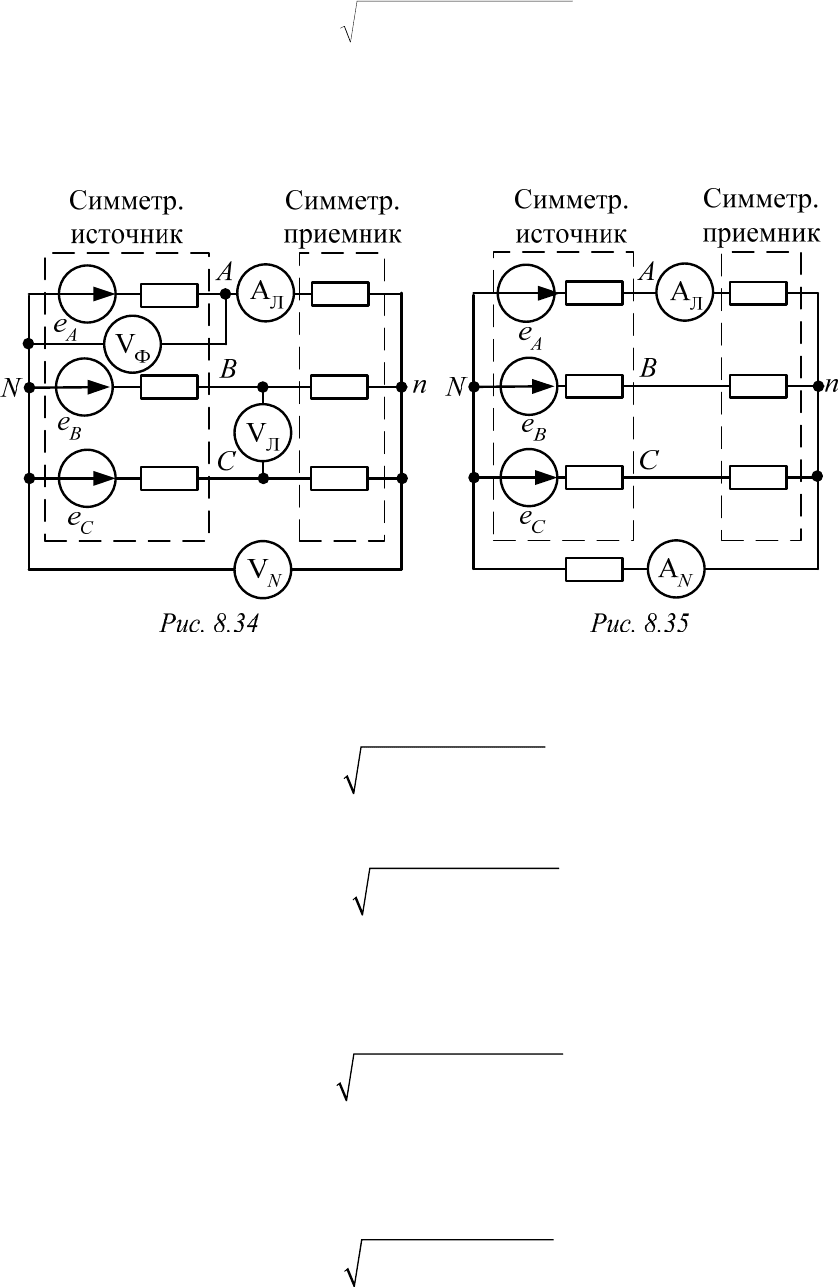
1. Звезда без нулевого провода (рис. 8.34)
Фазные напряжения источника содержат все вышеупомянутые
гармоники, поэтому
222
Ф 5
13
...U EEE
Линейные напряжения не содержат составляющих нулевой после-
довательности, а стало быть, и гармоник, кратных трем. В то же время
их составляющие прямой и обратной последовательностей превышают
соответствующие составляющие фазных напряжений в
3
раз, значит
Поэтому даже в симметричном режиме
ЛФ
3.UU
Линейные (они же фазные) токи не содержат гармоник, кратных
трем, поскольку эти гармоники образуют систему нулевой последова-
тельности и могут замыкаться лишь по нейтральному проводу:
2222
Л 15711
...IIIII
Поэтому в фазах источника и приемника отсутствуют падения
напряжения этих гармоник. Значит, согласно второму закону Кирхгофа,
между нейтральными точками N и n даже в симметричном режиме су-
ществует напряжение
2222
Л 15711
3( ...).U EEEE
135
...
2
15
2
9
2
3
EEEU
nN
,
в разложении в ряд Фурье которого основной является третья гармони-
ка. Следовательно, эту схему можно использовать в качестве утроителя
частоты.
2. Звезда с нейтральным проводом (рис. 8.35)
При тех же фазных ЭДС окажутся теми же самыми фазные и ли-
нейные напряжения. Но линейные токи на этот раз содержат все гармо-
ники
222
Л 135
...,I III
поскольку гармоники, кратные трем (и только они), замыкаются по ну-
левому проводу, так что
222
3915
3 ...
N
I III
3. Соединение треугольником
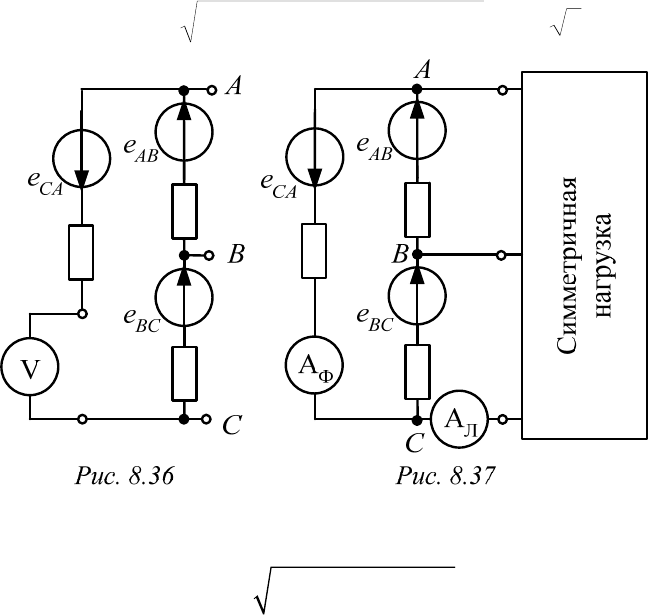
В фазах разомкнутого треугольника (рис. 8.36) ЭДС прямой и об-
ратной последовательностей в сумме дают нуль, поэтому напряжение на
разомкнутых зажимах содержит лишь гармоники, кратные трем:
222
3915
3...U EEE
Эта схема также может быть использована для утроения частоты.
Если цепь треугольника замкнута (рис. 8.37), то под действием
ЭДС гармоник, кратных трем, в его фазах и при отсутствии нагрузки
течет ток
222
Ф 3915
...IIII
136
Он создает падения напряжения, компенсирующие ЭДС, вызвав-
шие этот ток, поэтому линейные напряжения не содержат гармоник,
кратных трем. Значит, не содержат их при наличии нагрузки и линей-
ные токи (как и в случае со звездой). Поэтому
.3...)(3
Ф
2
11
2
7
2
5
2
1Л
IIIIII
В фазах генератора при наличии нагрузки токи содержат все гар-
моники:
222
Ф 135
...IIII
4. В заключение отметим, что в электродвигателях гармоники
1, 7, 13, … порядка создают магнитное поле, вращающееся в ту же сто-
рону, что и ротор (прямая последовательность). Гармоники порядка
5, 11, 17, … создают поле, вращающееся в противоположную сторону
(обратная последовательность). А гармоники, кратные трем, создают
пульсирующее магнитное поле (нулевая последовательность).
137
9. ЧЕТЫРЕХПОЛЮСНИКИ
9.1. Основные понятия и определения
При расчетах сложных электрических цепей нередко возникает
необходимость установить связь между напряжениями на двух парах
зажимов и токами, от них отходящими. В этом случае токи и напряже-
ния в остальных частях цепи интереса не представляют, хотя при реше-
нии задач учитываются параметры всей цепи.
Часть электрической цепи, имеющая две пары зажимов
для присо-
единения к остальной части цепи, называется четырехполюсником и
изображается на схеме, как показано на рис. 9.1. Зажимы, принадлежа-
щие одной паре, называются входными и обычно служат для присоеди-
нения к источнику энергии (1, 1). Два других, к которым обычно под-
ключается нагрузка, называются выходными (2, 2). Примеры: транс-
форматор, двухпроводная линия
электропередачи, мостовая схема. На
практике возможны и иные варианты подключения четырехполюсника.
Реальная схема соединений элементов, составляющих четырехпо-
люсник, и их параметры могут быть и неизвестны. В этом случае поль-
зуются некоторыми обобщенными величинами, достаточными для со-
ставления уравнений, связывающих напряжения и токи на зажимах че-
тырехполюсника.
Если параметры четырехполюсника не зависят
от режима работы,
он называется линейным, в противном случае – нелинейным.
Если он не содержит источников электрической энергии, то имену-
ется пассивным (
П, рис. 9.2), если содержит, то активным (А, рис. 9.1).
1
2
2
I
1
I
Активные четырехполюсники, в свою очередь, делятся на авто-
номные и неавтономные. У автономных существует напряжение хотя
бы на одной паре зажимов даже при отключении четырехполюсника от
остальной части цепи. У неавтономных в этом случае напряжение на
разомкнутых зажимах отсутствует. Их внутренние источники являются
зависимыми (пример – триод).
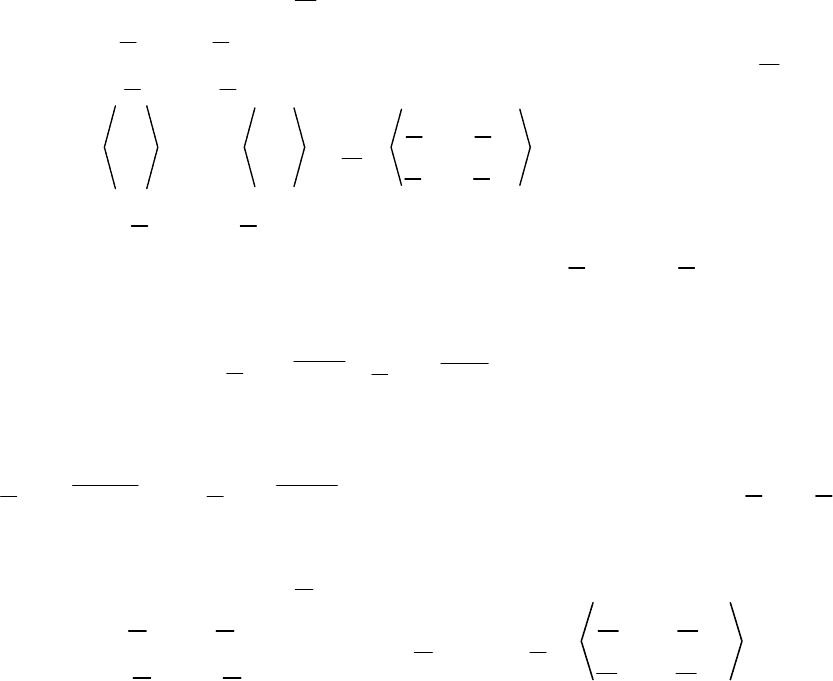
138
Если четырехполюсник удовлетворяет принципу взаимности, он
называется обратимым, в противном случае – необратимым. Отметим,
что пассивные линейные четырехполюсники всегда обратимы.
Если при перемене мест подключения входных и выходных зажи-
мов четырехполюсника его режим работы не меняется, то такой четы-
рехполюсник называется симметричным, в противном случае – несим-
метричным. В этом разделе (за
исключением одного параграфа) рас-
сматриваются
линейные пассивные четырехполюсники в устано-
вившемся синусоидальном режиме
. Поэтому все соотношения удобно
записывать в комплексной форме.
9.2. Основные уравнения четырехполюсника
Эти уравнения связывают напряжения и токи на входе и выходе че-
тырехполюсника. Возможны шесть вариантов записи основных уравне-
ний. При этом следует обратить внимание на возможные различные
направления токов в схеме рис. 9.2:
112 2
,.
I
II I
Уравнения в форме
Y
:
11 2
11 12
212
21 22
;
,
I
YU YU
I
YU YU
или в матричной записи
,IYU
1
11 12
1
21 22
2
2
где ;; .
IYY
U
YY
U
I
IU Y
Здесь
11 22
иYY
входные проводимости четырехполюсника от-
носительно первичных и вторичных зажимов,
12 21
иYY
взаимные
проводимости. При коротком замыкании выходных зажимов
2
(0)U
можно определить
1K
11
1K
;
I
Y
U
2K
21
1
.
I
Y
U
При обратном коротком замы-
кании
1
(0)U
и тех же направлениях токов можно найти
2OK 1OK
22 12
22
и .
II
YY
UU
Из принципа взаимности следует
12 21
.YY
Уравнения в форме
Z
:
11 2
11 12
212
21 22
;
,
UZIZI
UZIZI
или
,
UZI
где
11 12
21 22
,
ZZ
ZZ
Z
а
U
и I
– те же матрицы-столбцы, что и в предыдущем случае.
139
Здесь
11 22
иZZ
входные сопротивления четырехполюсника
относительно первичных и вторичных зажимов,
12 21
иZZ
взаим-
ные сопротивления. В режиме прямого холостого хода
2
(0)I
можно
определить
1
11
1X
;
U
Z
I
2X
21
1X
.
U
Z
I
При подключении источника с напряжением
2
U
к выходным за-
жимам и размыкании входных (обратный холостой ход –
1
0)I
можно
найти
1ОX
2
22 12
''
2ОX2ОX
;.
U
U
ZZ
II
Выполняется принцип взаимности:
12 21
.
Z
Z
Очевидно,
,
1
ZY
то есть взаимно обратны матрицы, а не их
компоненты. Легко заметить, что матричные уравнения
UZI
и
IYU
имеют вид закона Ома.
Уравнения в форме
А
:
122
11 12
11 12
12
21 22
12
122
21 22
;
или ,где .
,
UAUAI
AA
UU
AA
II
IAU AI
AA
Здесь коэффициенты
11 22
и
A
A
безразмерны,
12
A
имеет раз-
мерность сопротивления,
21
A
проводимости. При прямом включении
в режиме холостого хода
2
(0)I
определяются
11X
11 21
2X 2X
;.
UI
AA
UU
А в режиме короткого замыкания
2
(0)U
можно найти
11K
12 22
2K 2K
,.
UI
AA
II
Сравним последние формулы с описанием того же режима в фор-
ме
Y
. Тогда, учитывая, что
2K 2K
,
I
I
найдем
22
12 22
21 21
1
;.
Y
AA
YY
Продолжив сравнение в режиме холостого хода, обнаружим, что
140
11 11 22
11 21 12
12 21
;.
YYY
AAY
YY
Нетрудно убедиться, что
.1
21122211
AAAA
Способ более простого экспериментального определения коэффи-
циентов четырехполюсника в форме рассматривается ниже.
Уравнения в форме
B
:
211
11 12
11 12
21
21 22
21
211
21 22
;
или , где .
,
UBUBI
BB
UU
BB
II
IBUBI
BB
Как и в предыдущей паре формул, коэффициенты
11 22
иBB
безразмерны,
12
B
имеет размерность сопротивления,
21
B
проводимо-
сти. В режиме обратного холостого хода
1
(0)I
легко определяются
22X
11 21
1X 1X
;,
UI
BB
UU
а в режиме обратного короткого замыкания
1
(0)U
находятся
22K
12 22
1K 1K
;
UI
BB
I
I
(оба режима с изменением
направления токов). Если уравнения в форме
B
разрешить относитель-
но
11
и ,UI
то получим:
122
22 12
122
21 11
;
.
UBUBI
I
BU BI
Но перемена направлений токов
112 2
(, )
I
II I
должна при-
вести к форме
.A
Следовательно,
11 22 12 12 21 21 22 11
;;;.BA BA BA BA
Еще две формы записи уравнений связывают
1
U
,
2
I
с
2
,U
1
I
и
1
,
I
2
U
с
1
,U
2
.
I
Они употребляются реже.
11 2
11 12
11
22
21 2
21 22
;
Форма : или .
,
UHIHU
UI
IU
IHIHU
HH
112
11 12
11
22
212
21 22
;
Форма : или .
,
IGUGI
IU
UI
UGUGI
GG
А
