Эськов В.Д., Каталевская А.В., Сипайлов А.Г. Теоретические основы электротехники. Часть 1

Подождите немного. Документ загружается.

141

Разнообразие форм записей уравнений четырехполюсников обу-

словлено удобством использования той или иной формы при различных

схемах их соединений. Но при любой форме из четырех коэффициентов

четырехполюсников независимы только три.

9.3. Схемы соединения четырехполюсников

Рассмотрим наиболее часто встречающиеся схемы соединения че-

тырехполюсников на примере двух четырехполюсников, матрицы ко-

эффициентов которых известны, и заменим их одним эквивалентным,

связав его коэффициенты

A,Y,Z

с соответствующими коэффици-

ентами исходных четырехполюсников.

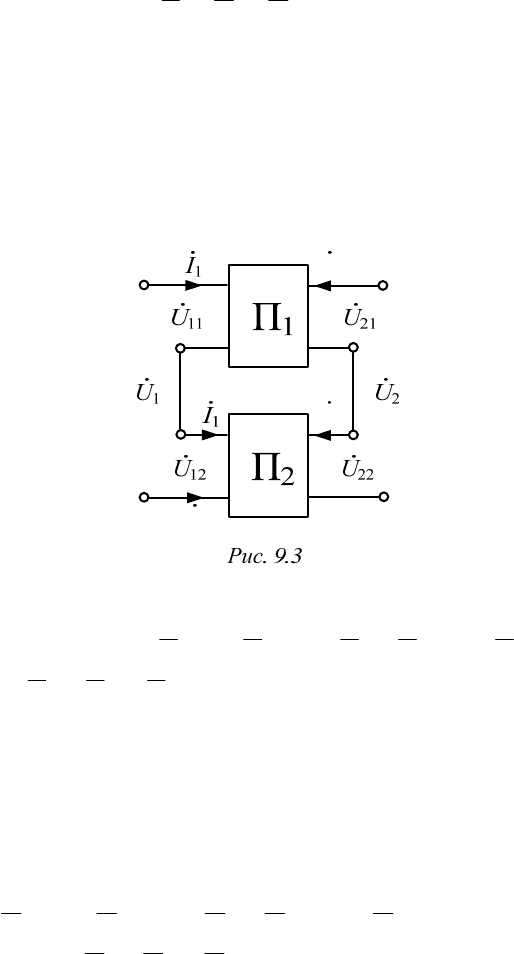
Последовательное соединение четырехполюсников – такое их со-

единение, при котором по входным зажимам обоих четырехполюсников

течет один и тот же ток



и по выходным зажимам – один и тот же ток





(рис. 9.3). В этом случае

11112 2 2122

;.UU U U U U 

    



Тогда в матричной форме





  

12 12

UUUZIZI(ZZ)IZI

    

Следовательно,

.)ZZ(Z



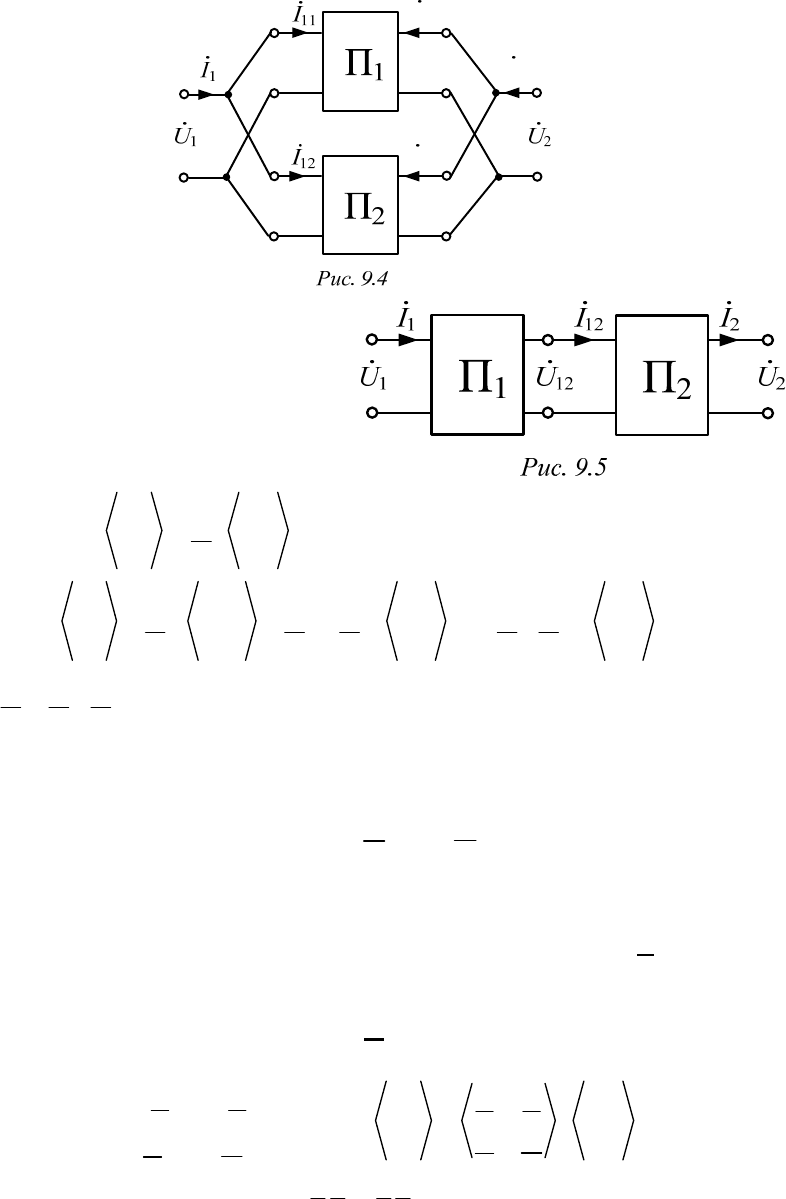
Параллельное соединение четырехполюсников – такое их соедине-

ние, при котором входные зажимы обоих четырехполюсников подклю-

чены к одному напряжению



и выходные зажимы обоих четырехпо-

люсников подключены к одному напряжению



(рис. 9.4).

Очевидно,

1 11 12 2 21 22

II III 

    

поэтому в матричной фор-

ме



    

12 12

II I YUYU(Y Y)UYU

     

Следовательно,

.)YY(Y





142



Каскадное соединение четы-

рехполюсников – такое их соедине-

ние, при котором входные зажимы

одного четырехполюсника (после-

дующего) подключены к выходным

другого (предыдущего) – рис. 9.5.

При этом

A



но

'' '"

112 2 2

UU U U

II I



     





AAA (AA)

  

тогда

.AAA

Для определения параметров эквивалентного четырехполюсника

при параллельно-последовательном или последовательно-параллельном

соединениях двух четырехполюсников используются соответственно

формы записи основных уравнений

и .GH

9.4. Экспериментальное определение

коэффициентов четырехполюсника в форме А

Наиболее употребительной формой записи основных уравнений

четырехполюсника является форма

А. Во многих учебниках, чтобы из-

бежать индексации обозначений, уравнения записывают в виде:

122

;

или ,

UAUBI

ICU DI





















 

где 1.AD BC





(9.1)

Найдем входные сопротивления четырехполюсника в режимах хо-

лостого хода и короткого замыкания при прямом и обратном включении

с этими же обозначениями коэффициентов.

143

Прямое включение

Холостой ход

0; .





(9.2)

Короткое замыкание

0; .





(9.3)

Обратное включение

Холостой ход

0; .







(9.4)

Короткое замыкание

0; .









(9.5)

Из этих пяти уравнений можно найти 4 неизвестных коэффициента

различными способами. Наиболее простые формулы получаются при

использовании соотношений (9.1, 9.2, 9.4, 9.5). Из (9.2):

;



из (9.5):

;BAZ

из (9.4) и (9.2):





Подстановка B, C, D в (9.1) позволяет найти

К2Х2

Х1





, а за-

тем и остальные коэффициенты четырехполюсника.

Заметим, что

1X 2X

1K 2K



9.5. Схемы замещения четырехполюсника

Поскольку в основных уравнениях четырехполюсника только три

независимых параметра, то и схемы замещения четырехполюсников

можно составить из трех сопротивлений, соединив их в Т- или П-схему

(рис. 9.6 и 9.7). Установим связь этих сопротивлений с коэффициентами

четырехполюсника в форме

А.

Т-схема (рис. 9.6). Найдем входные сопротивления четырехполюс-

ника в режимах прямого и обратного холостого хода и обратного корот-

кого замыкания. Очевидно,

1X 1 2X 2 2K 2

11 1

;; .

ZZ Z Z Z Z

    



1Х

Т 10 0

2Х 2К 1X

Тогда 1; ;

ZY С Y

ZZ Z





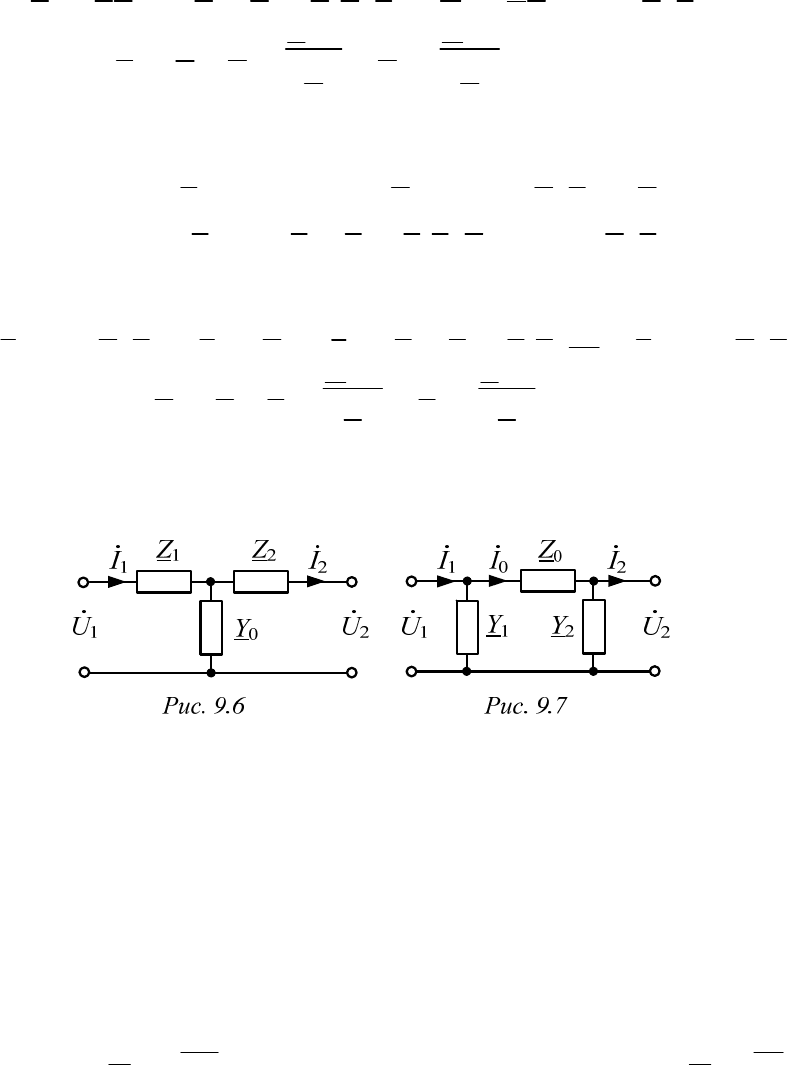
144

01 2

Отсюда ;; .

YCZ Z



 

П-схема

(рис. 9.7). Составим уравнения по законам Кирхгофа:





02 2 1 20 2 2

20020

;1;

IUY UU IZU ZY ZI     

      

10 1 2 2

112120 01

()(1).IIUYUYYYYZ I ZY     

   

Сравнивая эти формулы с основными уравнениями четырехполюс-

ника, найдем:

ППП 0 П

02 0 1 2 12 01

1; ; ;1.

ZY B Z C Y Y YYZ D ZY     

01 2

Отсюда ;;.

ZBY Y



 

Cоотношения между сопротивлениями Т- и П-схем подчиняются

формулам, описывающим эквивалентные преобразования схем звезда–

треугольник.

9.6. Передаточные функции

Передаточными функциями, или коэффициентами передачи,

называют отношения комплексных амплитуд, или комплексных дей-

ствующих значений, электрических величин на выходе и входе четы-

рехполюсника в заданном режиме работы. Именно выходная величина

делится на входную, а не наоборот.

Отношения одноименных величин – коэффициент передачи по

напряжению





и коэффициент передачи по току





–

представляют собой безразмерные комплексные величины, зависящие

от частоты. Применительно к четырехполюсникам, которые использу-

ются в усилительных устройствах, они называются коэффициентами

усиления по напряжению и току.

Т 2K 1 2 1 2 0 Т 2X 2 0

;1.

AZ Z Z Z Z Y D CZ Z Y 

145

Отношения разноименных величин – передаточное сопротивление





и передаточная проводимость







имеют размерности

сопротивления и проводимости и также являются комплексными вели-

чинами, зависящими от частоты.

Зависимости модулей этих комплексных коэффициентов от часто-

ты представляют собой амплитудно-частотные, а их аргументов – фазо-

частотные характеристики четырехполюсника, имеющие важное значе-

ние при исследовании устройств автоматики и радиотехники.

Если четырехполюсник нагружен на комплексное сопротивление

то передаточные функции можно выразить через это сопротивле-

ние и коэффициенты формы

.А

Логично использовать именно эти ко-

эффициенты четырехполюсника, если речь идет о передаче энергии или

сигнала от источника к приемнику.

22 22

122 122

22 22

122 122

;;

UU I I

UAUBI ICUDICZ D

UU I I

ICUDI UAUBIAZB

   





   





 

 

 

 

9.7. Симметричный четырехполюсник

Как отмечалось выше, если поменять местами входные и выходные

зажимы симметричного четырехполюсника, то режим его работы не из-

менится. При этом в основных уравнениях в форме

А коэффициенты

меняются местами. Поэтому у симметричного четырехполюсника

должно быть

.DA



В других формах записи уравнений (Z и Y) будут,

очевидно, справедливыми соотношения:

2211



2211

YY 

Таким

образом, симметричный четырехполюсник характеризуется только дву-

мя независимыми параметрами.

Коэффициенты симметричного четырехполюсника (рис. 9.8 и 9.9)

для Т- и П-схем соответственно равны:

T Т 0 Т 00

1, (1), ;

DZYBZZYС Y



   

ПП 0 П 00

1, , (2).

DZYBZCYZY  

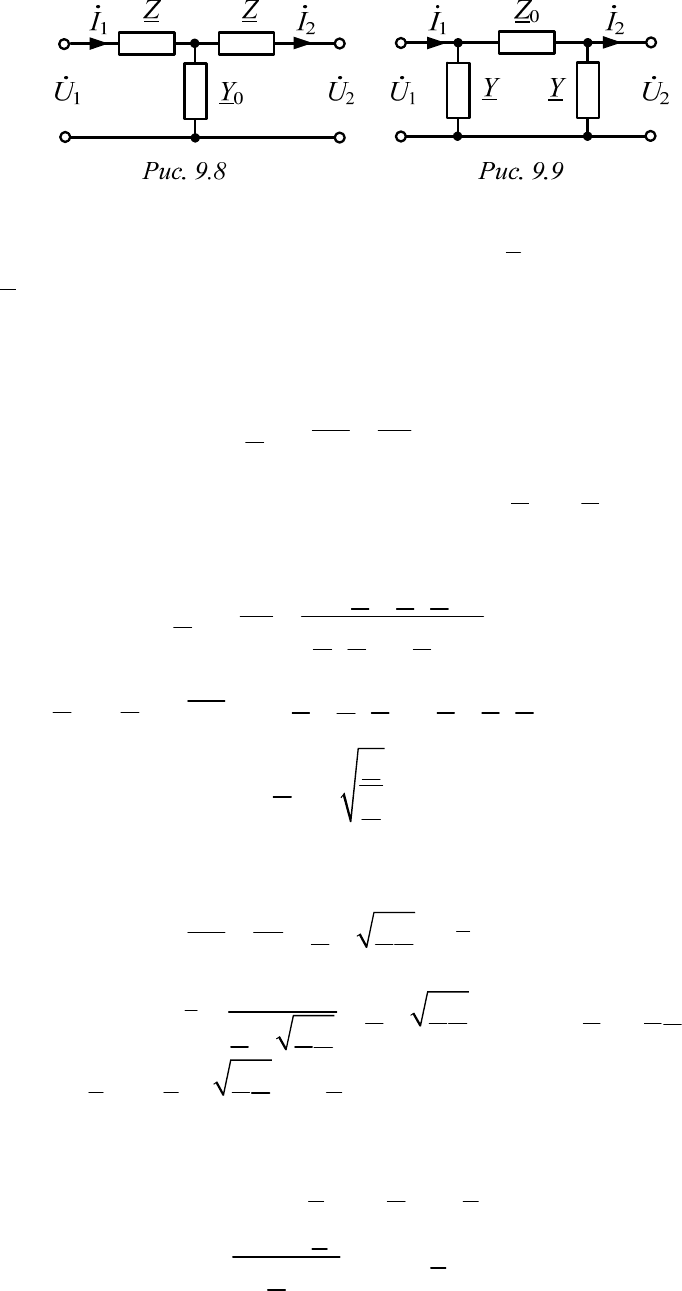
146

Введем понятия вторичных параметров симметричного четырехпо-

люсника – характеристического сопротивления

и постоянной пе-

редачи Г. Характеристическим сопротивлением четырехполюсника

называется такое сопротивление, при подключении которого к выход-

ным зажимам четырехполюсника входное сопротивление последнего

окажется точно таким же, т. е.





Режим работы четырехполюсника, в котором



, называется

режимом согласованной нагрузки. Из основных уравнений четырехпо-

люсника в этом режиме следует:

(/)

()

UABZ

CZ A I













Так как





то

CZ A BZ





откуда



Из определения характеристического сопротивления следует, что в

режиме согласованной нагрузки

BC e

 



В свою очередь,

,eABC

ABC







так как

 CBA

Поэтому ch ; shГ.ABC 

Уравнения симметричного четырехполюсника в гиперболических

функциях имеют вид:



12 2

ch(Г)sh(Г);

ch Г

sh Г .

UU IZ















 





147

В режиме согласованной нагрузки постоянная передачи

Г ln ln ln( ) j .

BC a b

 



11 2 2

Если e и e,тоUU U U







j( )

11 1 1

22 2

ln ln ln ln[e ] ln j( ).

UU U U

UU U











 



Постоянная ослабления (коэффициент затухания)

11 11

22 22

ReГ ln ln ln ln

UIUI

   



показывает, насколько отличаются логарифмы действующих значений

напряжений (или токов) на входе и выходе четырехполюсника в режиме

согласованной нагрузки.

Постоянная (коэффициент) фазы

1212

Im Г arg( ) arg( ) arg( ) arg( )bUUII   



показывает, насколько отличаются фазы напряжений (или токов) на

входе и выходе четырехполюсника в режиме согласованной нагрузки.

Уравнения в гиперболических функциях могут быть записаны и

для несимметричного четырехполюсника, но в них будут участвовать,

наряду с постоянной передачи, два характеристических сопротивления

(относительно входных и выходных зажимов).

9.8. Цепная схема

Каскадное соединение нескольких одинаковых симметричных че-

тырехполюсников называется однородной симметричной цепной схе-

мой, а каждый из этих четырехполюсников – звеном цепной схемы

(рис. 9.8).

Выразим параметры эквивалентного четырехполюсника

ЭC

через параметры одного звена. Для этого включим на выходе цепной

схемы сопротивление нагрузки





При этом по определе-

148

нию окажется





Рассуждая аналогичным образом и для осталь-

ных звеньев, получим

121

III













В свою очередь,







123

1121

H23H

23 H

...

Г ln ln ln ln ... ln Г.

...

UUU U

UUUU

UU U U

 

 



 



  

Таким образом,

ЭЭ

ГГ ;;; .

nanabnbZ Z 

Уравнения в гиперболических функциях для цепной схемы имеют

вид:

1H H

ch( Г)sh(Г);

sh( Г)

sh( Г).

UU n IZ n

IIn















 





9.9. Схемы замещения и основные уравнения

автономного активного четырехполюсника

Если автономный активный четырехполюсник отключить от

остальной части цепи, то на его разомкнутых входных и выходных за-

жимах возникнут напряжения одновременного (!) холостого хода

1XХ



2XХ



(рис. 9.11, а). Очевидно, такие же напряжения возникнут и на

зажимах схемы рис. 9.11, б, где активный четырехполюсник заменен

пассивным. Последний получается из исходного активного, если за-

мкнуть накоротко внутренние источники ЭДС и отключить внутренние

источники тока.

а б

Рис. 9.11

2XX

1XX

Пассивный четырехполюсник можно заменить Т-схемой замеще-

ния (рис. 9.12), параметры которой определяются так же, как в схеме

рис. 9.6.

Уравнения, описывающие состояние этой схемы, имеют вид:

149

11XХ 22XХ 2

122XХ 2

();

().

UU AU U BI

ICUU DI



 





 





   

 

Можно составить и другую схему замещения – с источниками тока,

задающие токи которых равны токам короткого замыкания

1КЗ



2КЗ



определяемым при одновременном (!) замыкании входных и выходных

зажимов (рис. 9.13).

В этом случае пассивный четырехполюсник удобнее заменить

П-схемой замещения, параметры которой определяются так же, как и в

схеме рис. 9.7. Уравнения, описывающие состояние этого варианта схе-

мы замещения активного четырехполюсника, имеют вид:

12 22КЗ

11КЗ 222КЗ

();

().

UAUBII

II CU DI I









 





 

   

9.10. Круговая диаграмма четырехполюсника

Круговой диаграммой называется геометрическое место точек, по

которым перемещается конец вектора входного тока четырехполюсника

при изменении величины сопротивления нагрузки от 0 до  и неизмен-

ном угле сдвига фаз между напряжением и током на выходе четырехпо-

люсника. Для линейного четырехполюсника это геометрическое место

(годограф) представляет собой дугу окружности – отсюда и название.

Докажем, что выражение







где

const,M



const,a 

const,





при изменении n от 0 до  представляет собой уравнение ду-

ги окружности, проходящей через начало координат.

После приведения к общему знаменателю получаем

Me M





На векторной диаграмме (рис. 9.14) этой формуле соответствуют

два вектора

( и ),

ОКМ

 

сумма которых





при любых значениях n

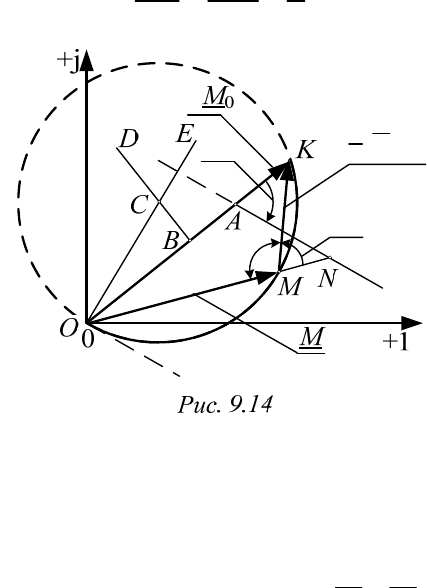
150

остается постоянной. Причем не меняется и угол



между этими векто-

рами, так же как и угол







при вершине М треугольника ОМК,

вследствие чего он оказывается вписанным в окружность.

Отсюда следует, что конец вектора





при изменении n переме-

щается по дуге ОМК окружности, для которой отрезок ОК является

хордой. Иными словами, вышеприведенное выражение при указанных

условиях действительно описывает дугу окружности на комплексной

плоскости.

Покажем, как найти положение точки М для любого значения n.

Отложим от точки А вдоль ОК отрезок

OA a



в некотором масштабе.

Проведем из точки А прямую



под углом (–



) к АК. Если





то

треугольники OAN и OMK подобны, поскольку имеют общий угол при

вершине O и одинаковые углы







Из подобия треугольников следу-

ет равенство отношений

NKMn

OA OM a















Значит, если

,OA a

то



в том же масштабе. Линия AN’

называется линией переменного параметра. Откладывая на ней различ-

ные отрезки AN, соответствующие разным значениям n, и соединяя их

концы N с точкой O, можно получить на пересечении с дугой необхо-

димое положение точки М. При



имеем



(),OM OK

а при

n 

точка М сливается с точкой O, секущая ON становится касатель-

ной (показана пунктиром). При этом точка N уйдет в бесконечность и

окажется

.ON AN





Отсюда ясно, что центр окружности С, частью ко-

торой является дуга ОМК, лежит на пересечении двух перпендикуляров:

к середине хорды

()

DOK

и к линии переменного параметра

().OE AN



