Эськов В.Д., Каталевская А.В., Сипайлов А.Г. Теоретические основы электротехники. Часть 1
Подождите немного. Документ загружается.

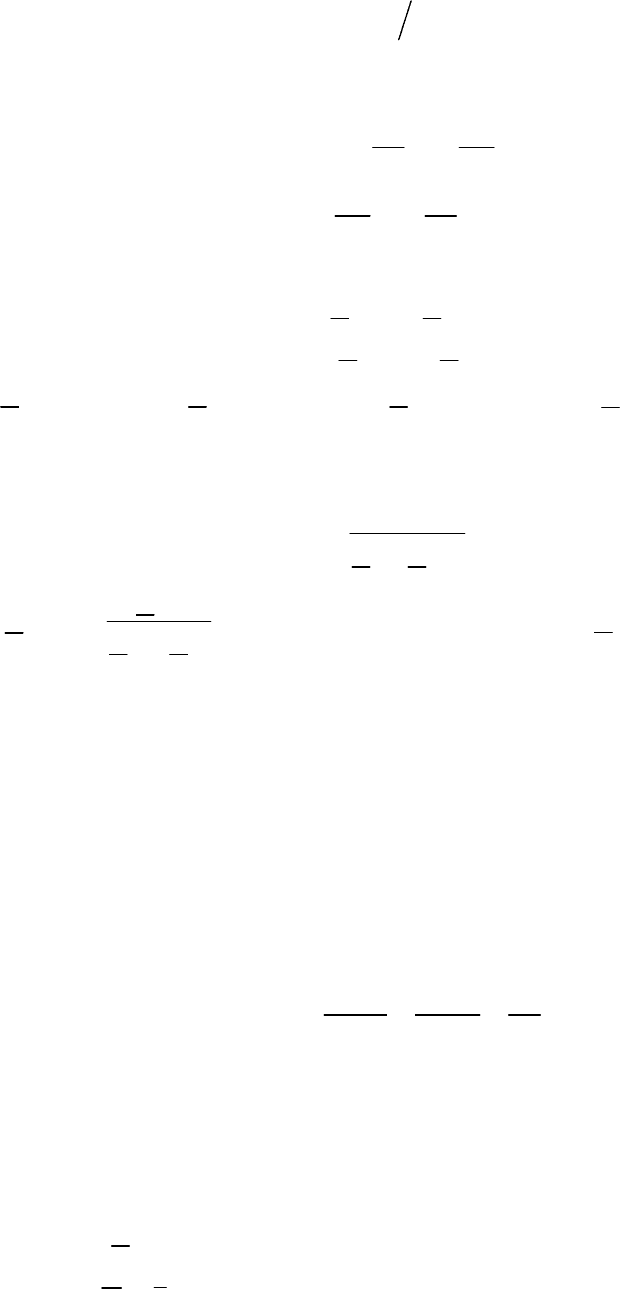
81
ХХ ХХ
ВН НН
.nU U
По второму закону Кирхгофа для мгновенных значений токов и
напряжений
12
1111
21
22 2 2
;
0.
di di
uRiL M
dt dt
di di
Ri L M u
dt dt
В комплексной форме
11 2
1
22 1
2
;
,
M
M
UZIZ I
UZIZI
где
11
1
j;
L
Z
RX
22
2
j;
L
ZR X
j;
M
M
ZX
22
H
.UZI
В результате решения системы уравнений можно найти
1
I
и запи-
сать его в виде:
1
1
1BH
,
U
I
ZZ
где
2
BH
2H
M
Z
Z
ZZ
вносимое сопротивление, а
H
Z
комплексное
сопротивление нагрузки.
Вносимым называется такое сопротивление, которое следовало бы
внести в первичную цепь, чтобы учесть влияние нагрузки вторичной
цепи трансформатора на ток в его первичной цепи. Можно показать, что
при уменьшении сопротивления нагрузки активно-индуктивного харак-
тера увеличивается вносимое сопротивление, имеющее активно-
емкостный характер (поэтому ток
1
I
увеличивается).
Если
12
,UU
то при
11L
R
X
и одинаковом магнитном потоке в
обеих обмотках коэффициент трансформации будет равен:
11 1
12
ХХ
ВН
ХХ
НН
,
L
M
I
Xw
I
Xw
U
n
U
12
где иww
число витков первичной и вторичной обмоток.
Пример 5.3 (рис. 5.17)
1
12 2
:10Ом;40Ом;20Ом;
LM
X
L
Дано RR X X
2
H
(20 j20) Ом;1A.ZI
Найти
1
,U
1
,I
построить векторную диаграмму.
82
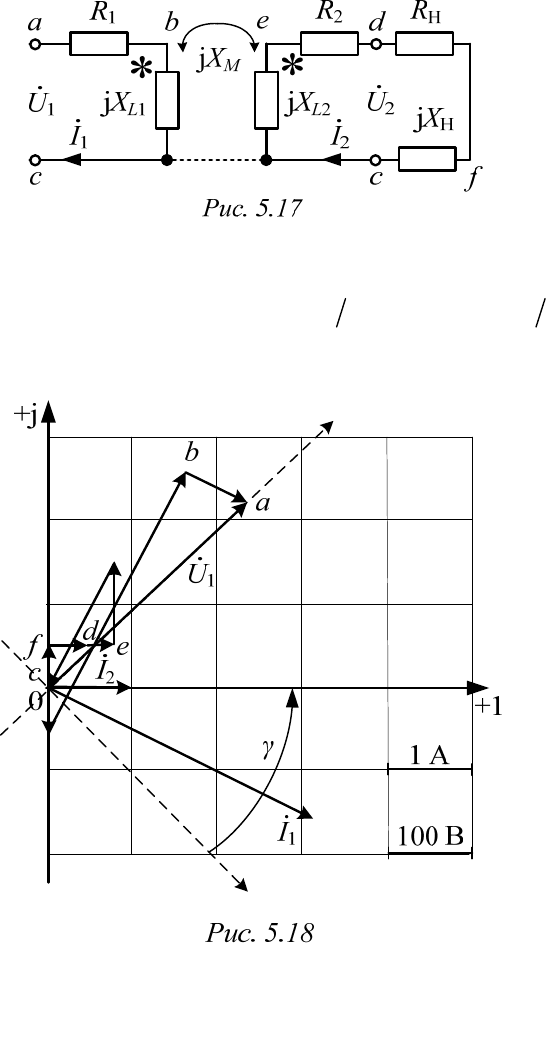
Решение
Построение диаграммы (рис. 5.18) начинаем с осей комплексной
плоскости и выбора масштабов
(40Bдел.; 1 A дел.).
UI
mm
Из
начала координат строим вектор
2
1A.I
b
+1
e
+j
По закону Ома
2H 2p 2H 2a
j j20 B; 20 B;
fc df
UIXU UIRU
22 2 2
10 B; j j40 B.
ed e e L
URI UIX
Точка с является общей для обеих обмоток (в реальных трансфор-
маторах она заземляется по соображениям техники безопасности). По-
местим эту точку в начало координат
(0)
c
и начертим из нее вектор
,
f
c
U
к концу которого пристроим вектор
.
df
U
Затем отложим векторы
2H 2a
20 B;
df
UIRU

83
ed
U
и
,
ee
U
так же пристраивая начало последующего к концу преды-
дущего.
Из диаграммы
(30 j60) B.
ce fc df ed e e
UUUUU
Это
напряжение взаимной индукции во вторичной обмотке, поэтому
1
(3 j1,5) A.
(j )
ce
M
U
I
X
Вектор тока
1
I
проводим из начала координат. Вычисляем состав-
ляющие падения напряжения в первичной обмотке:
211
j j20 B; j (60 j120) B;
bc M bb L
UXI UXI
11
(30 j15) B,
ab
URI
и строим их по порядку на комплексной плоскости. Теперь можно
найти и входное напряжение:
j43,4
1
90 j85 123,8 B.
ac b c bb ab
UU U U U e
На этом примере удобно продемонстрировать еще один метод рас-
чета простейших цепей синусоидального тока c одним источником –
метод пропорционального пересчета.
Предположим, что задано напряжение на входе первичной обмотки
трансформатора
j90
1
250 BUe
и требуется определить токи. Тогда,
выполнив предыдущий расчет, сравним расчетное значение напряжения
1
U
c заданным и найдем комплексный коэффициент пересчета
ЗАД
j90
j46,6
1
РАСЧ
j43,4
1
250
2,02 .
123,8
U
e
Ke
U
e
На этот коэффициент нужно умножить расчетные значения токов, что-
бы получить искомые. Таким образом, окажется
-j26,6 j46,6 j20 j46,6
12
3,35 2,02 6,77 A; 2,02 A.Ie e e I e
Что же касается векторной диаграммы, то ее можно оставить без
изменения, увеличив масштабы в
2,02K
раз и повернув оси по часо-
вой стрелке на угол
arg 46,6 .K
Эти оси показаны на рис. 5.18
пунктиром.
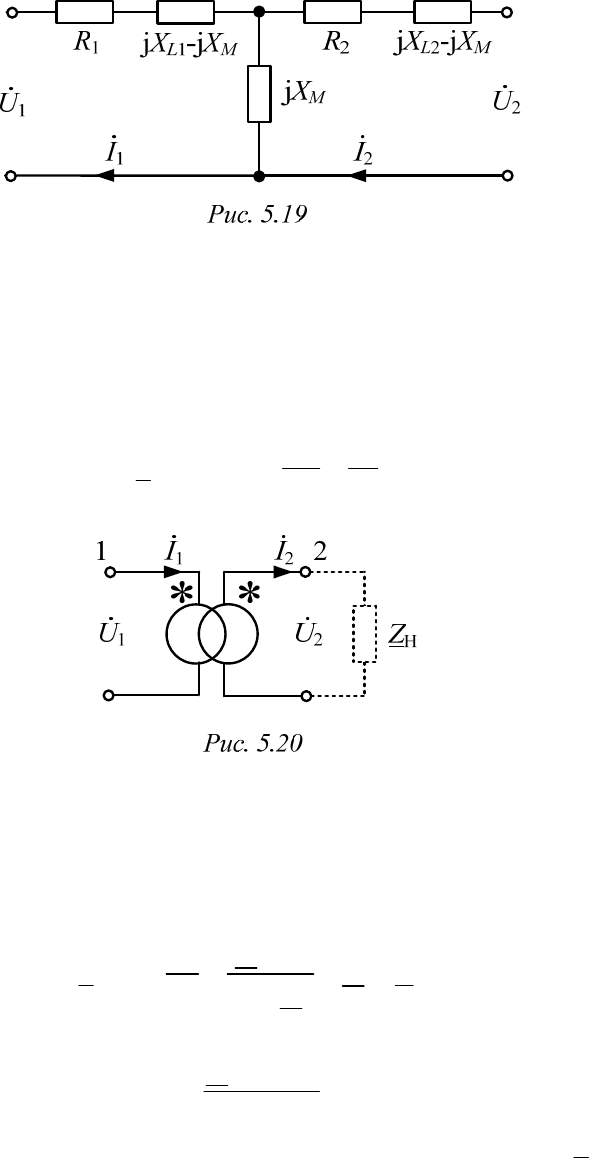
Отметим также, что при необходимости нетрудно «развязать» схе-
му замещения трансформатора (рис. 5.17), используя прием, проиллю-
стрированный на рис. 5.14. В результате эквивалентная комплексная
схема замещения трансформатора без индуктивной связи будет иметь
вид, показанный на рис. 5.19.
84
5.8. Идеальный трансформатор
Идеальный трансформатор представляет собой четырехполюсный
элемент схемы (рис. 5.20), который при любых условиях сохраняет
неизменным комплексный коэффициент трансформации:
j
12
21
.
UI
Nne
UI
1
2
Чтобы свойства реального трансформатора с ферромагнитным сер-
дечником приближались к свойствам идеального, должны выполняться
следующие условия:
112 2СВ
; ; 1.
LL
RXR XК
При наличии нагрузки входное сопротивление трансформатора
2
12
1BX
H
12
,
(/)
UNU
Z
NZ
IIN
а комплексная мощность
j2
22
111 2
€
€
= e .
€
NU I
SUI S
N
Если коэффициент трансформации вещественное число
(),Nn
то
12 1 2
;.PP QQ
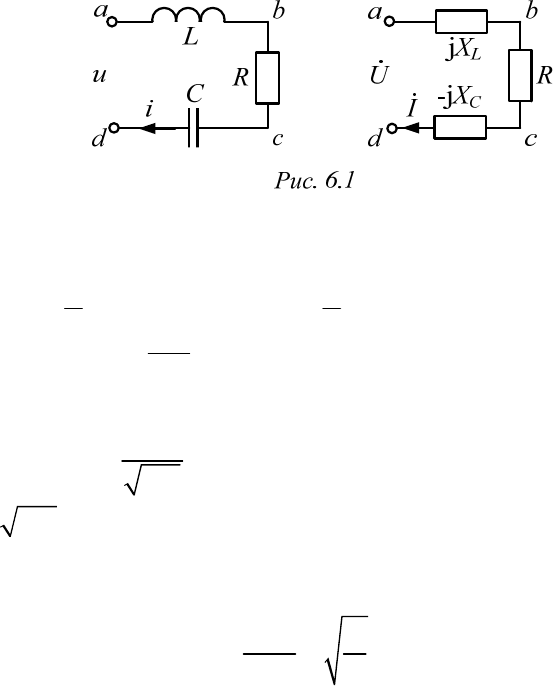
85
6. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Электрическим (фазовым) резонансом называется явление совпа-
дения по фазе тока и напряжения на входе пассивного двухполюсника,
содержащего индуктивности и емкости. Рассмотрим это явление на
примере простейших цепей.
6.1. Резонанс при последовательном соединении R, L, C
(рис. 6.1)
Для того чтобы по определению оказалось
arg arg ,UI
должны
быть равны нулю аргумент и мнимая часть комплексного сопротивле-
ния цепи: arg arg( / ) 0, Im Im( j ) 0,
L
C
ZUI ZRXXXX
т. е.
,
L
C
XX
или
1
.L
C
Отсюда
2
1.
L
C
Значит, резонанса мож-
но достичь, изменяя либо L, либо C, либо
. В последнем случае резо-
нансная частота
0
1
,
LC
а период свободных незатухающих колеба-
ний
0
2TLC
(формула Томсона).
Равные друг другу при резонансе индуктивное и емкостное сопро-
тивления можно выразить только через индуктивность и емкость:
0
0
1
.
L
L
CC
Эта независящая от частоты величина называется характеристиче-
ским сопротивлением контура.
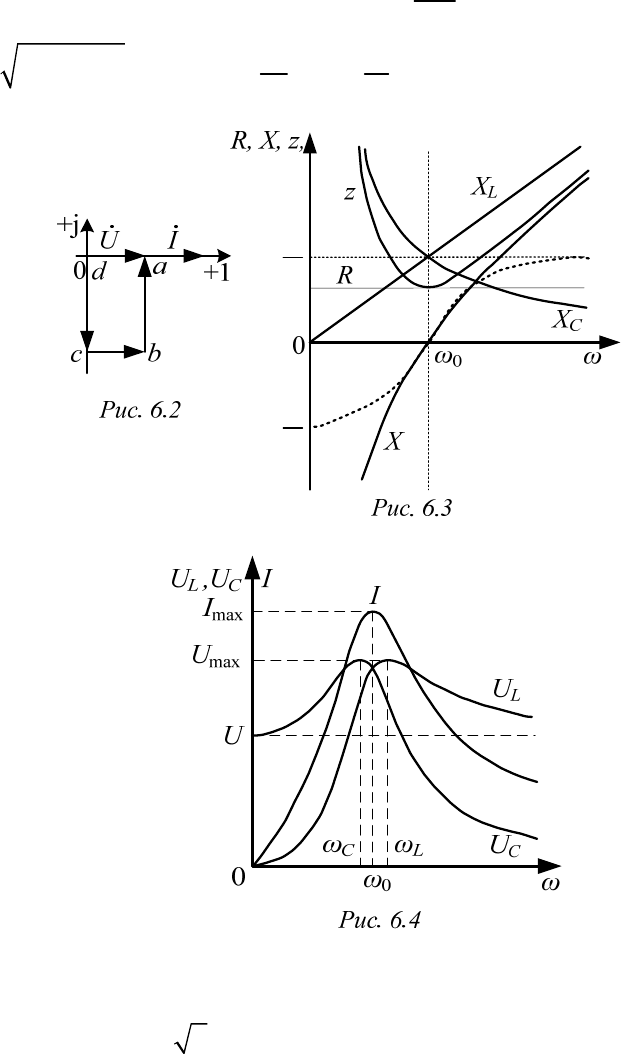
Векторная диаграмма для рассматриваемой схемы показана на
рис. 6.2, где
;
cd C
UIX
;
bc
UIR
;
ab L
UIX
.UU
ad
В данном случае резонанс происходит за счет взаимной компенса-
ции напряжений на реактивных элементах схемы
,
LC
UU
поэтому его
называют резонансом напряжений. Одновременно
R
UU
и может ока-
заться
.
C
UU
Для этого должно быть
,
LC
XXR
или
.R
86
Добротность контура
//
C
QRUU
показывает, во сколько раз
напряжение на каждом из реактивных элементов превышает напряже-
ние на входе цепи в режиме резонанса.
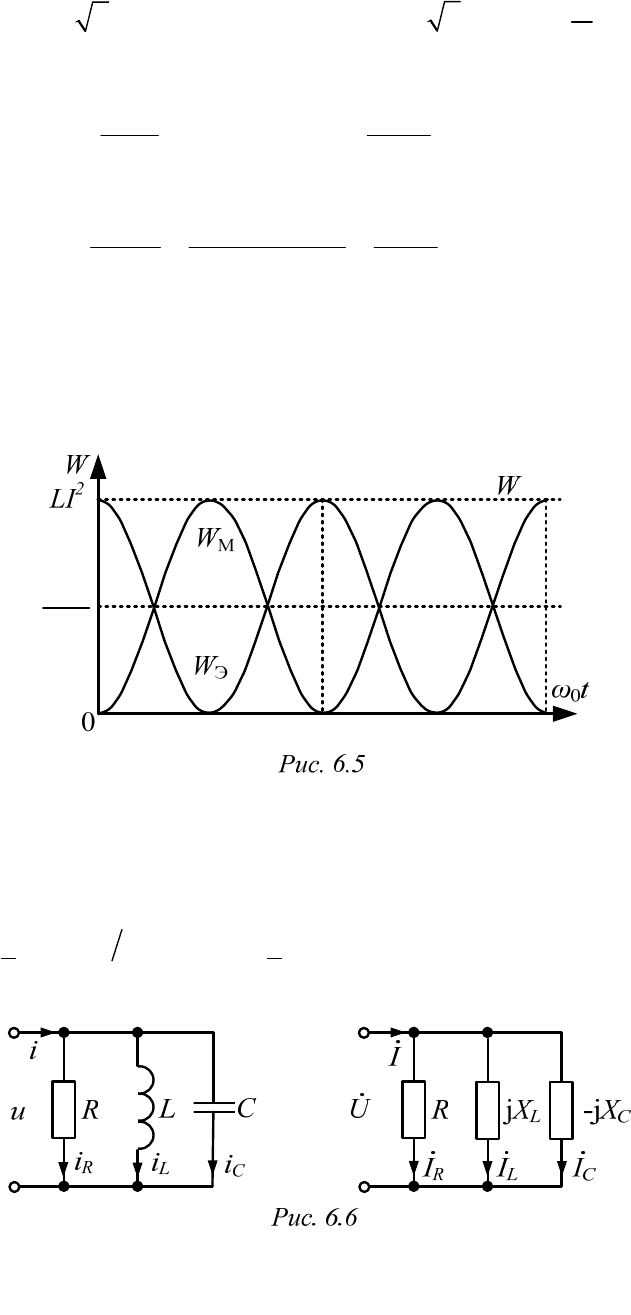
На рис. 6.2, 6.3 построены частотные характеристики цепи в соот-
ветствии с формулами:
1
() const; ; ; ;
LC LC
R
XLX XXX
C
22
;;;;.
LLCC
XU
zRX arctg I UIXUIX
R
z
2
2
Кривая
()z
имеет минимум, а кривая
()I
максимум при
0
.
Что касается кривых
()
L
U
и
(),
C
U
то они имеют максимум
при добротности
2,Q
причем связь между частотами, при которых
эти максимумы достигаются, такова:
2
0
.
LC
87
Энергетические соотношения при резонансе
Пусть
0
2sin( ),iI t
тогда
0
2sin( ).
2
CC
uIX t
Энергия, запасенная в магнитном поле,
22
22
00
sin ( ) 1 cos(2 ) .
22
м
Li LI
WLIt t
Энергия, запасенная в электрическом поле,
22 2
2
0
Э 0
2
0
cos ( )
1cos(2 ).
22
C
С uI t
LI
Wt
C
Их сумма не зависит от времени:
2
ЭМ
const.WW LI
Это
означает, что источник компенсирует потери в сопротивлении R, кото-
рые возникают при обмене энергией между электрическим полем кон-
денсатора и магнитным полем катушки (рис. 6.5).
2
2
L
I
2
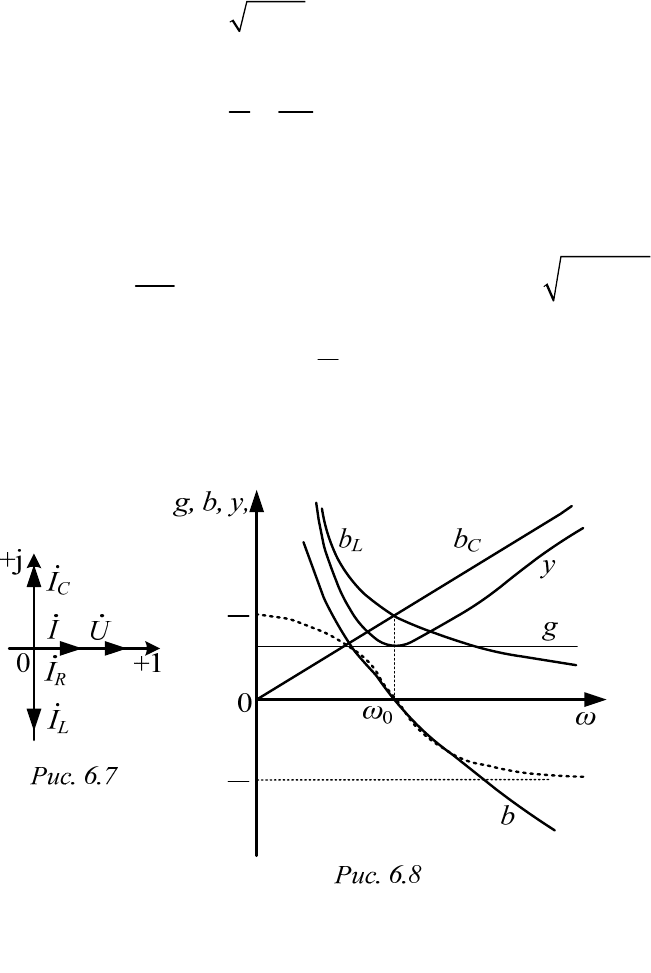
6.2. Резонанс при параллельном соединении R, L, C (рис. 6.6)
Для того чтобы по определению оказалось arg( ) arg( ),
I
U
должно
быть
arg( ) arg( ),YIU
или
Im( ) Im( j ) 0,
CL
Ygbbbb
откуда
LC
bb
и снова
2
1.
L
C
Векторная диаграмма построена на рис. 6.7, где
;.
LC R
II II
88
Может оказаться
,
C
II
для этого необходимо выполнение усло-
вия
, или /,где
LC
bb g g CL
характеристическая
проводимость цепи.
Добротность контура
C
I
Q
g
I
показывает, во сколько раз ток в
реактивном элементе больше тока на входе схемы.
Частотные характеристики (рис. 6.8) строятся в соответствии с
формулами:
22
1
( ) const; ; ; ; ;
LC LC
gbbCbbbygb
L
arctg .
b
g
Что касается зависимостей токов от частоты, то они подобны зави-
симостям соответствующих проводимостей от частоты.
2
2
Энергетические процессы сходны с процессами предыдущего при-
мера: происходит обмен энергией между электрическим и магнитным
полями, так что их суммарный запас остается неизменным.
Поскольку в данном случае резонанс происходит за счет взаимной
компенсации токов в реактивных элементах схемы, то он носит назва-
ние резонанса токов. Ток на входе двухполюсника при этом
оказывает-
ся минимальным.
89
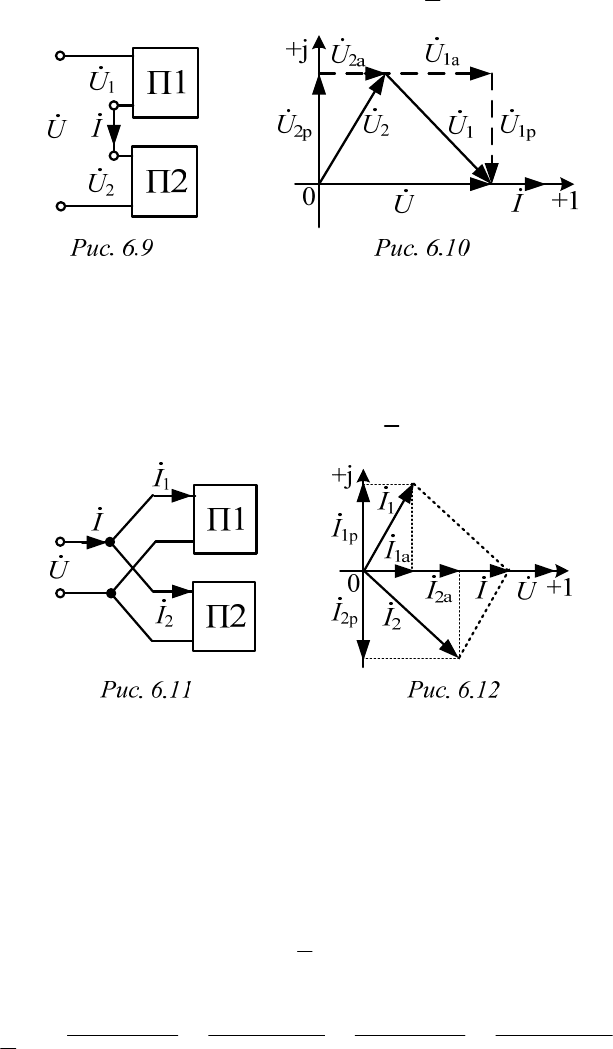
6.3. Резонанс в сложной цепи
Резонанс в цепи с последовательным соединением двухполюсни-
ков, содержащих реактивные элементы разного характера (рис. 6.9), ко-
торый происходит за счет взаимной компенсации реактивных состав-
ляющих напряжений на этих двухполюсниках (рис. 6.10), называется
резонансом напряжений.
Его условия:
1p 2p
;UU
1a 2a
;UU U
ЭЭ
Im 0.ZX
Резонанс в цепи с параллельным соединением двухполюсников, со-
держащих реактивные элементы разного характера (рис. 6.11), который
происходит за счет взаимной компенсации реактивных составляющих
токов в этих двухполюсниках (рис. 6.12), называется резонансом токов.
Его условия:
1p 2p
;II
1a 2a
;II I
ЭЭ
Im 0.Yb
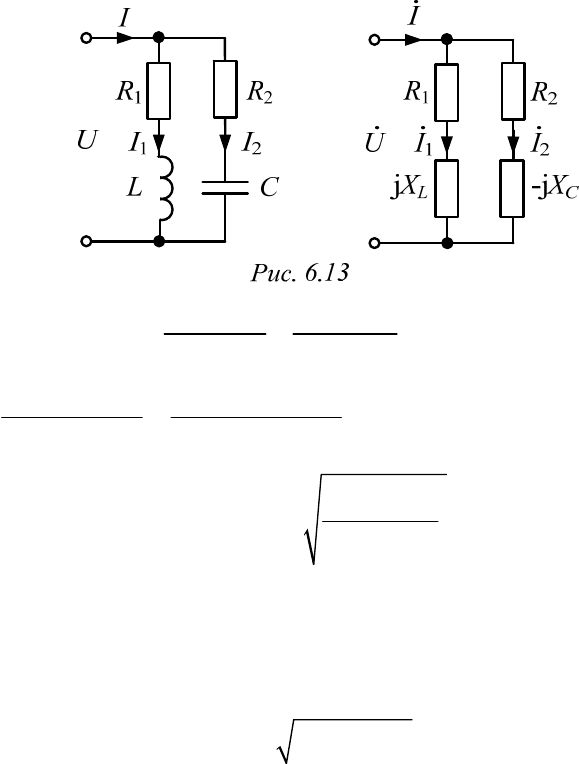
Пример 6.1
Определить резонансную частоту, если известны параметры
1
,
R
2
,
R
L, C схемы, изображенной на рис. 6.13.
Решение
Воспользуемся условием резонанса токов
ЭЭ
Im( ) 0.bY
Комплексная проводимость цепи
22
2
2
22
1
1
21
Э
j
j
j
1
j
1
C
C
L
L
CL
XR
XR
XR
XR
XRXR
Y
.
90
При резонансе
Э
2222
12
0.
C
L
LC
X
X
b
RX RX
Тогда
PP
222 222
1P 2P
,
1
LC
RLRC
откуда
22
1
P0
22
2
()
.
()
R
R
Частные случаи:
1.
12
.
R
RR
При этом
P0
,
как в простейших цепях.
2.
.R
Тогда
P
0,
резонанс при любой частоте.
3.
12
;0,RRR
наиболее реальный случай, тогда
22
P0
1/.R
Резонанс в реальных цепях. При последовательном соединении
элементов в режиме резонанса напряжение на каждом из этих элемен-
тов может оказаться больше, чем на входе цепи. В сильноточных цепях
такой резонанс приведет к повреждению изоляции и аварийным режи-
мам, поэтому с ним стараются бороться, избегая соответствующего со-
четания параметров. В слаботочных
цепях (радиотехника, телевидение)
за счет настройки контура в резонанс удается выделить сигнал опреде-
ленной частоты, усилить его.
Резонанс токов может сыграть полезную роль и в сильноточных
цепях: установка на подстанциях батарей конденсаторов (параллельно
нагрузке, имеющей активно-индуктивный характер, настроенных в ре-
зонанс с ней) позволяет улучшить коэффициент мощности
(cos ),
при-
близив его к 1 и снизив тем самым потери энергии при ее передаче от
источника к приемнику.
В слаботочных цепях резонанс токов применяется для ослабления
сигналов определенной частоты.
