Эськов В.Д., Каталевская А.В., Сипайлов А.Г. Теоретические основы электротехники. Часть 1
Подождите немного. Документ загружается.

41
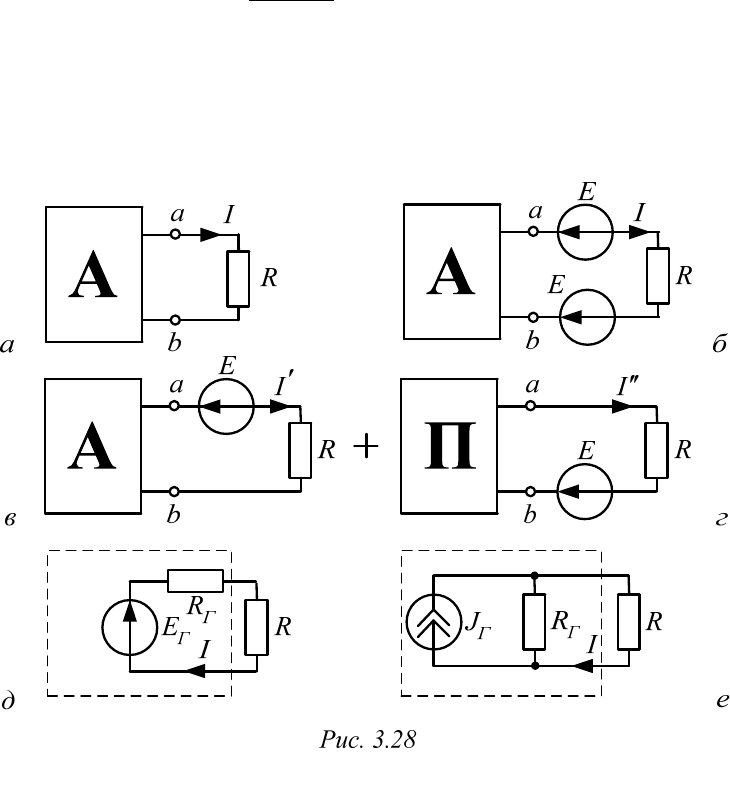
Докажем эту теорему с помощью схем рис. 3.28 и покажем, как
определяются вышеупомянутые параметры.
Ток I (рис. 3.28, а) не изменится, если последовательно в ветвь
нагрузки двухполюсника включить две одинаковых ЭДС противопо-
ложной полярности (рис. 3.28, б). По принципу наложения
,III
причем первая составляющая учитывает все источники активного двух-
полюсника и ЭДС Е (рис. 3.28, в), направленную против тока, а вторая –
лишь оставшуюся ЭДС Е (рис. 3.28, г). Если
,0
I
то в первой подсхе-
ме реализован режим холостого хода двухполюсника и
.
ХХ
UE
Во
второй подсхеме
,
Э
RR
E
II
где
Э
R
эквивалентное сопротивле-
ние пассивного двухполюсника относительно зажимов нагрузки
(рис. 3.28, д). Пассивный двухполюсник получается из активного заме-
ной источников ЭДС короткозамкнутыми ветвями и отключением вет-
вей с источниками тока.
Таким образом, во второй подсхеме по сравнению с исходной схе-
мой активный двухполюсник заменен простой эквивалентной схемой.
Теорема доказана и найдены параметры эквивалентного генератора
напряжения:
ГХХ
ГЭ
;
.
EU
R
R
(3.10а)

42
Используя известное преобразование, можно перейти к схеме экви-
валентного генератора тока (рис. 3.28, е), в которой
Г
ГКЗ
Г
ХХ
ГЭ
КЗ
;
.
E
JI
R
U
RR
I
(3.10б)
В последних простых схемах (рис. 3.28, д, е) легко находится ток:
KЗ
ГХХ ГГ Г
KЗ
ГГ Г Г Г
, или , где .
1/
I
E
UJR E
II I
R
RR R R R RR R
3.6.5. Теорема о линейных соотношениях
В линейной цепи при изменении какого-либо одного из ее парамет-
ров (ЭДС, задающего тока или сопротивления) любые две величины
(токи или напряжения) связаны линейным соотношением вида
.b
x
ay
Докажем теорему для случая изменения одной из ЭДС, например
.
m
E
По принципу наложения можно записать
.00
;
nmnmn
k
mkm
k
IEGIIEGI
Здесь в
0k
I
и
0n
I
собраны составляющие токов
k
I
и
,
n
I
не зави-
сящие от
m
E
. Исключая
m
E
из этих выражений, получим
.
00
baI
G
G
II
G
G
II
n
nm
km
nk
nm
km
nk
00
Здесь ;.
km km
kn
nm nm
GG
abII
GG
Аналогичным образом доказывается теорема и при изменении за-
дающего тока какого-либо источника. Для доказательства теоремы в
случае изменения одного из сопротивлений следует применить теорему
компенсации.
3.7. Метод наложения
Метод основан на принципе наложения. Его использование дает
заметное упрощение расчета в несложных схемах с небольшим количе-
ством источников. Любой ток (или напряжение) можно определить в
виде суммы составляющих от действия каждого источника в отдельно-
сти (обычно с применением эквивалентных преобразований).
Рассмотрим порядок расчета на примере привычной уже схемы
рис. 3.9 с
теми же данными.
43
Пример 3.4
Определить ток
1
I
методом наложения.
Решение
1. Изобразим столько подсхем, сколько в исходной схеме источ-
ников энергии (рис. 3.29–3.31). В каждой из них действует только один
источник. Остальные источники тока отключаем, а источники ЭДС за-
меняем короткозамкнутыми ветвями (замыкаем накоротко).
2. Каждую из подсхем преобразуем до одного контура, сохраняя
в ней сопротивление
1
,
R
после чего находим ток по закону Ома.
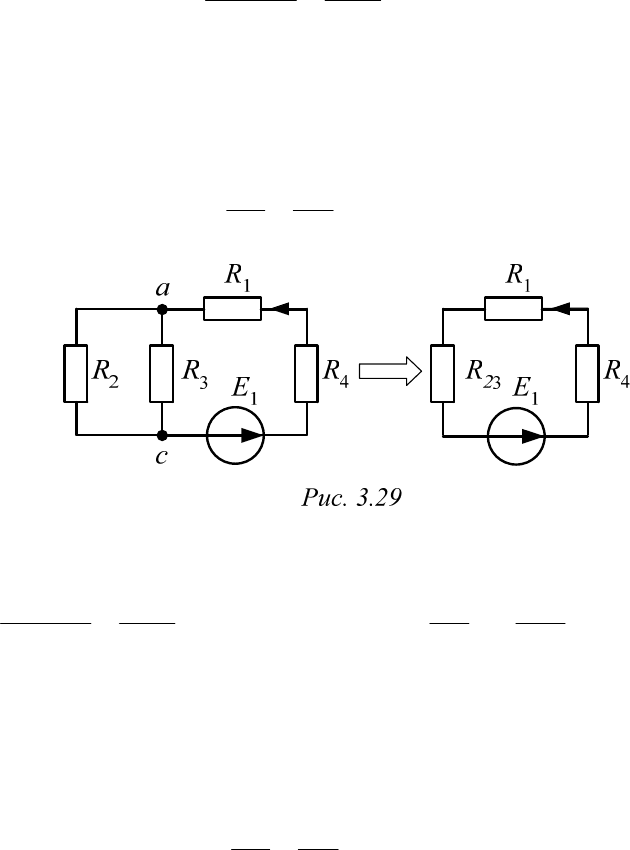
В первой подсхеме (рис. 3.29) для этого достаточно заменить па-
раллельно соединенные сопротивления
3
R
и
2
R
одним эквивалентным:
Затем можно найти эквивалентное сопротивление последовательно
включенных элементов
Э 1234
1 1,2 4 6,2 ОмRRR R
и воспользоваться законом Ома
1
Э
14
2, 26 А.
6, 2
E
I
R
1
I
1
I
Во второй подсхеме (рис. 3.30) производится замена пассивной и ак-
тивной ветвей, соединенных параллельно, одной эквивалентной. При этом
32 Э
Э
23 Э
319 11,4
11,4 Ви 1, 84 А.
23 6,2
RE E
EI
RR R
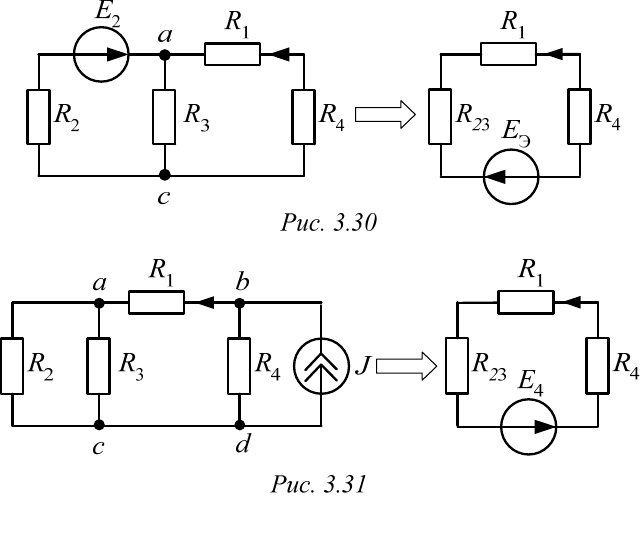
Наконец, в третьей подсхеме (рис. 3.31) переходим от схемы с источ-
ником тока J, подключенного параллельно сопротивлению
4
R
, к схеме с
источником ЭДС
44
44 16 В,EJR
включенным последовательно
с этим сопротивлением. И, как в первой подсхеме, вводим
23
R
, тогда
4
Э
16
2,58 .
6, 2
E
I
А
R
23
23
23
23
1, 2 Ом.
23
RR
R
RR
44
1
I
1
I
1
I
1
I
3. В соответствии с принципом наложения находим искомый ток:
1
2,26 1,84 2,58 3 А.IIII
Результат тот же, что и полученный другими методами.
Возможно также применение метода наложения с использованием
входной и взаимных проводимостей, а также коэффициентов передачи
по току, которые заранее определены в реальной электрической цепи
экспериментально.
Метод наложения нельзя использовать для определения мощностей
приемников в виде суммы составляющих в каждой из подсхем, по-
скольку мощность является квадратичной функцией тока:
2
.PI R
3.8. Метод эквивалентного генератора
Метод основан на теореме об эквивалентном генераторе и предна-
значен для определения тока в одной из ветвей, по отношению к зажи-
мам которой остальная часть схемы рассматривается как активный
двухполюсник. Используется в трех вариантах, алгоритмы расчета ко-
торых рассмотрены ниже.
3.8.1. Метод холостого хода
1. Сопротивление
Н
R
, в котором нужно найти ток, отключается
от схемы рис. 3.32, а. Затем определяется напряжение между образо-
вавшимися зажимами. Это напряжение холостого хода генератора
ГXX
EU
(рис. 3.32, б).

45
2. Источники ЭДС замыкаются накоротко, источники тока от-
ключаются, двухполюсник становится пассивным (рис. 3.32, в), после
чего определяется эквивалентное сопротивление относительно тех же
зажимов. Это внутреннее сопротивление генератора
.
ГЭ
RR
3. Определяется искомый ток по выведенной выше формуле:
XX
ГН
,
U
I
R
R
(3.10в)
которую иногда называют формулой Тевенена–Гельмгольца.
3.8.2. Метод короткого замыкания
1. Сопротивление
Н
,
R
в котором нужно найти ток (рис. 3.33, а),
замыкается накоротко, и в этой короткозамкнутой ветви (рис. 3.33, б)
любым методом определяется ток. Это ток короткого замыкания гене-
ратора
.
ГКЗ
II
2. Как в предыдущем методе, определяется
ГЭ
R
R
(рис. 3.33, в).
3. Определяется искомый ток по формуле
КЗ
Н
Г
,
1
I
I
R
R
(3.10г)
которую иногда называют формулой Нортона–Поливанова.
46
3.8.3. Метод холостого хода и короткого замыкания
1. Определяется напряжение холостого хода, как в способе 3.8.1.
2. Определяется ток короткого замыкания, как в способе 3.8.2.
3. Определяется сопротивление эквивалентного генератора по
формуле
.
КЗ
XX
Г
I
U
R
4. Искомый ток определяется по любой из формул: 3.10в
или 3.10г.
Чаще используется первый вариант метода эквивалентного генера-
тора (3.8.1). Второй (3.8.2) целесообразно применять в тех случаях, ко-
гда есть несколько ветвей, параллельных той, в которой определяется
ток. Третий (3.8.3) используется, если сопротивление генератора нельзя
найти с помощью известных преобразований. Он применим и в
тех слу-
чаях, когда активный двухполюсник представляет собой «черный
ящик». В этом случае напряжение холостого хода и ток короткого за-
мыкания определяются экспериментально.
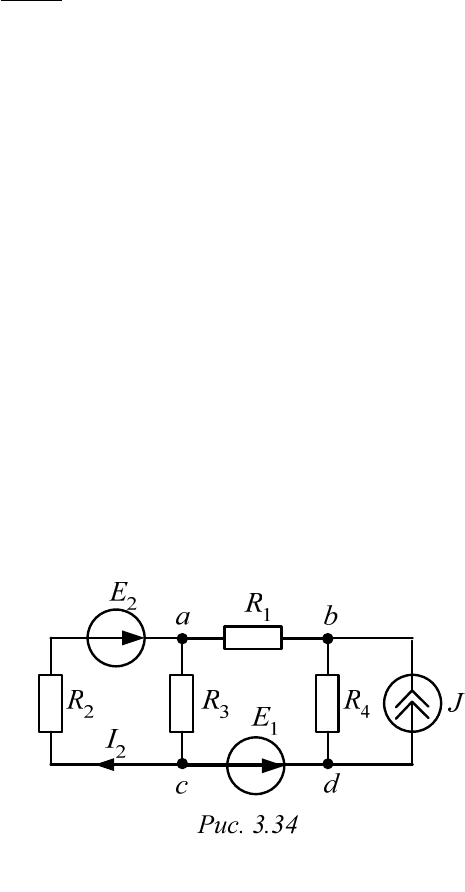
Применим первые два способа к схеме 3.9, которая повторена на
рис. 3.34 с теми же исходными данными.
Пример 3.5
Определить ток
2
,I
используя метод холостого хода и метод ко-
роткого замыкания.
Метод холостого хода
После отключения сопротивления
2
R
схема рис. 3.34 принимает
вид, показанный на рис. 3.35, а.
По второму закону Кирхгофа
.
X32XX
IREUU
cf
Неизвестный ток определим методом контурных токов. Для конту-
ра cabda уравнение с контурными токами имеет вид
.)(
14X413
EJRIRRR
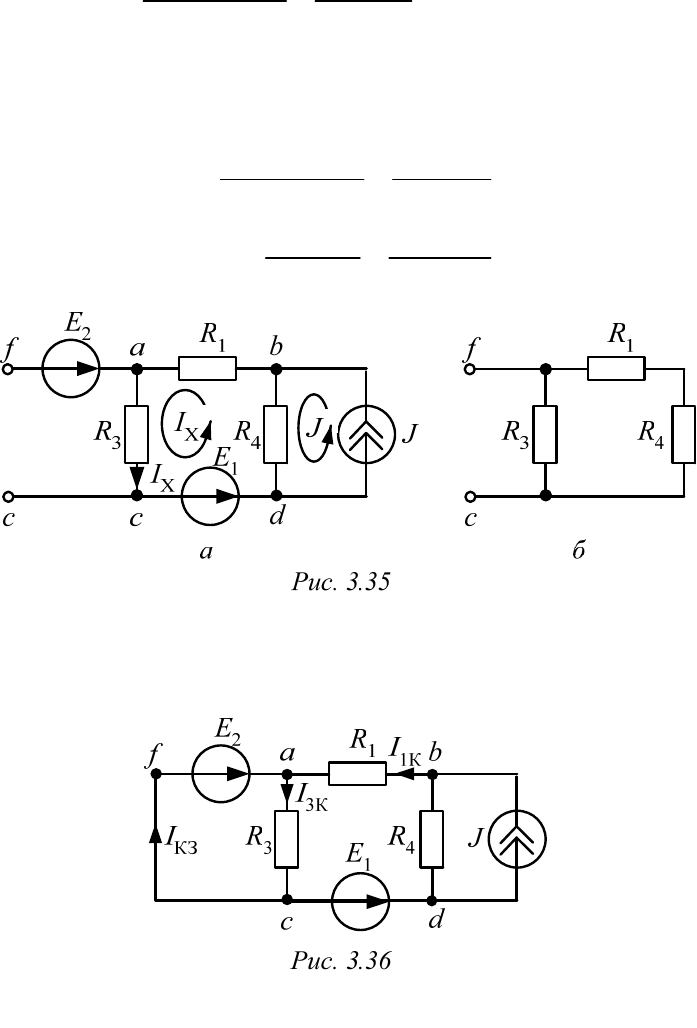
47
41
X
314
44 14
Отсюда 3, 75 A.
314
RJ E
I
RRR
Г XX
Тогда 19 3 3,75 7,75 В.EU
Если в этой схеме заменить ЭДС закороткой и отключить источник
тока, то получится схема, изображенная на рис. 3.35, б. Тогда
31 4
Г
314
()
3(1 4)
1,875 Ом.
314
cf
RR R
RR
RRR
Искомый ток равен:
Г
2
Г 2
7,75
2 А.
1,875 2
E
I
RR
Метод короткого замыкания
После замыкания сопротивления
2
R
накоротко схема рис. 3.34
приобретает вид, показанный на рис. 3.36.
По первому закону Кирхгофа
КЗ 3К 1К
.III
Для определения токов
3К
I
и
1К
I
воспользуемся методом узловых
потенциалов, принимая
0.
cf
Тогда
21
19 В;14В
ad
EE
и уравнение с узловыми по-
тенциалами для узла b имеет вид

48
14 1 4
11 1 1
.
ba d
J
RR R R
Отсюда
14 4 1
14
414 194 141
21,2 B.
14
ad
b
JR R R R
RR
1К 3К
13
21,2 19 19
2, 2 A; 6,33 A;
13
ba a
II
RR
КЗ
6,33 2, 2 4,13 A.I
Искомый ток с учетом найденного выше
Г
1, 875 ОмR
равен:
1
1
2
2 КЗ
Г
2
14,131 2А.
1, 875
R
II
R
Естественно, он имеет то же значение, что и полученное другим
способом.
3.9. Топологические матрицы и их применение к расчету цепей
Чтобы формализовать процесс составления уравнений, описываю-
щих состояние цепи с учетом ее геометрической структуры (топологии),
используются топологические матрицы.
Эти матрицы удобно составлять по графу схемы без особенностей,
т. е. схемы, в которой нет источников тока и ветвей с сопротивлением
равным нулю. Если таковые все же имеются, то их следует исключить,
используя
перенос источника тока в ветви контура и перенос источника
ЭДС через узел с последующим объединением узлов с одинаковыми
потенциалами.
Узловая (структурная) матрица A имеет столько столбцов, сколь-
ко граф ветвей, и столько строк, сколько граф независимых узлов (учи-
тываются все узлы, кроме опорного). В клетку матрицы, лежащую на
пересечении k-й строки и m-го столбца, вписывается 1, если ветвь m
направлена от узла k; –1, если она направлена к этому узлу; и 0, если
ветвь m
не подключена к данному узлу.
Если расширить матрицу за счет опорного узла, добавив соответ-
ствующую строку, то у такой матрицы сумма компонентов в каждом
столбце должна равняться нулю.
Контурная матрица B имеет столько столбцов, сколько граф вет-
вей, и столько строк, сколько граф независимых (главных) контуров.
В клетку матрицы, лежащую на пересечении k-й строки и m-го столбца
вписывается 1, если направление m-й ветви совпадает с направлением
49
обхода k-го контура; –1, если она направлена в противоположную сто-
рону; 0, если данная ветвь не входит в этот контур. Если граф планар-
ный (на чертеже его ветви не пересекаются), то обычно в качестве неза-
висимых контуров выбираются ячейки графа, а направление обхода –
против часовой стрелки.
Если расширить контурную матрицу за счет
внешнего контура,
в котором выбрать направление обхода по часовой стрелке, то сумма
компонентов в каждом столбце такой расширенной матрицы окажется
равной нулю.
Матрицу
В, составленную для главных контуров, называют мат-
рицей главных контуров. Направление обхода каждого из главных кон-
туров совпадает с направлением соответствующей хорды.
Связь между контурной и узловой матрицами определяется формулами
ФФ
и .БВ =0 ВБ =0
Здесь
Ф
Б
и
В
– транспонированные матрицы (меняются местами
столбцы и строки).
Уравнения Кирхгофа с помощью топологических матриц записы-
ваются следующим образом
по первому закону
,
Б I=0
(3.11)
по второму закону
.
BRI=BЕ (3.12)
Здесь
I и E – матрицы-столбцы токов и ЭДС ветвей, причем ЭДС
записывается со знаком «плюс», если ее стрелка совпадает с направле-
нием ветви;
R – диагональная (остальные компоненты равны 0) матрица
сопротивлений ветвей.
Уравнения с узловыми потенциалами в матричной форме:
уу
,
G=J
(3.13)
где
У
G
квадратная матрица узловых проводимостей; – матрица-
столбец узловых потенциалов;
У
J
матрица-столбец узловых задаю-
щих токов.
В свою очередь, матрицы узловых проводимостей и задающих то-
ков можно построить таким образом:
T
УУ
;, GAGAJ AGE
где
1
GR диагональная матрица проводимостей ветвей;
T
A
транспонированная узловая матрица.
Если обе части уравнения (3.13) умножить слева на
1
y
,
G
то будут
найдены узловые потенциалы
1
уу
.
=G J
Напряжения между узлами можно найти по формуле

50
T
,
UA
а токи по закону Ома для активных ветвей в матричной форме:
().
IGUE
(3.14)
Уравнения с контурными токами в матричной форме:
,
kk
RJE
(3.15)
где
k
R
квадратная матрица контурных сопротивлений; J – матрица-
столбец контурных токов;
k
E
матрица-столбец контурных ЭДС.
Матрицы контурных сопротивлений и контурных ЭДС могут быть
построены следующим образом:
;,
kk
T
R=BRB E BE
где
T
B
транспонированная контурная матрица.
Контурные токи равны:
1
,
kk
JR E
а токи ветвей находятся по формуле
T
.
I=B J
Пример 3.6
Составить уравнения по законам Кирхгофа для схемы рис. 3.9,
используя узловую и контурную матрицы.
Решение
На рис. 3.37, а показана схема, полученная после исключения ис-
точника тока в исходной схеме путем его переноса в правом контуре.
На рис. 3.37, б – направленный граф преобразованной схемы, у которого
жирными линиями выделено дерево. Здесь
Э 14 Э 14
14 4 4 30 B; 1 4 5 Ом.ЕЕRJ R R R
Узлы b и d устранены преобразованием. Поэтому матрица
A имеет
только одну строку и три столбца, а матрица
В – две строки и три
столбца. Ниже приводятся матрицы
A и В для этой схемы.
