Эськов В.Д., Каталевская А.В., Сипайлов А.Г. Теоретические основы электротехники. Часть 1

Подождите немного. Документ загружается.

Из выражения тока смещения следует:

2cos( ) 2sin( )

CiCi

u idt I t IX t



 



  



2sin( ).





Отсюда

IXU



(и здесь закон Ома), причем

коэффициент пропорциональности





называется емкостным

сопротивлением. Кроме того,



 





поэтому говорят, что

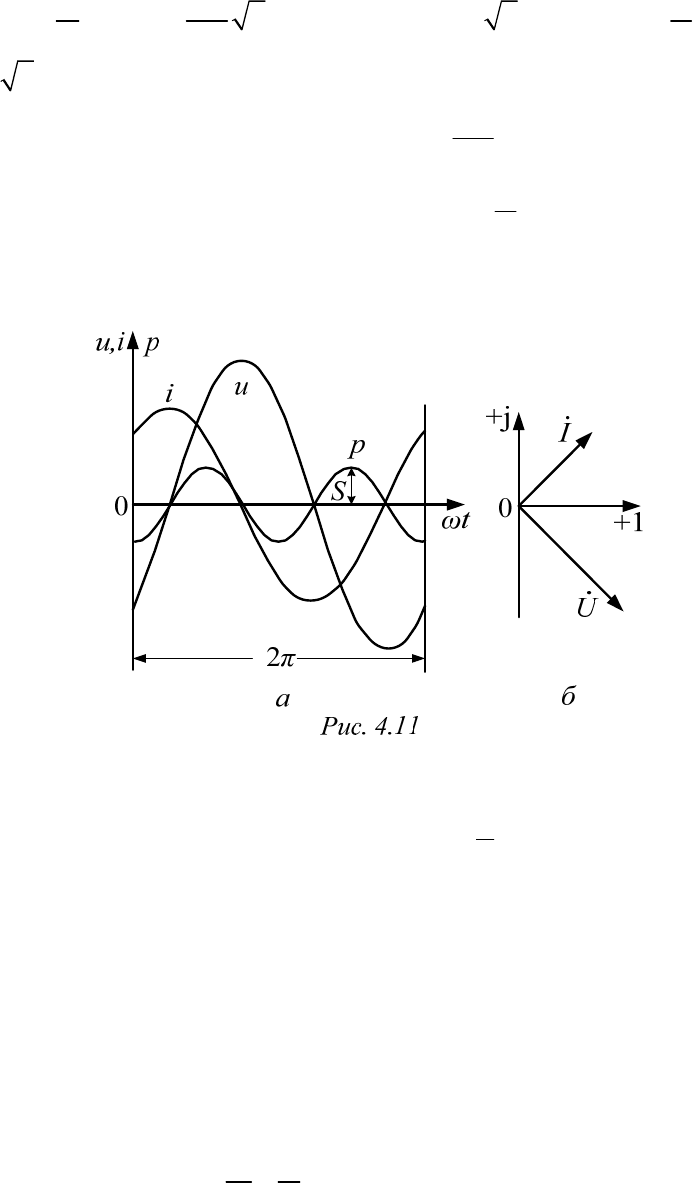
напряжение на емкости отстает от тока на 90 градусов. Векторная диа-

грамма показана на рис. 4.11, б.

Закон Ома для амплитуд и комплексов токов и напряжений спра-

ведлив и в этом случае:

j( )

;(j).

Cm m C C СС

UIXUIXe XI











Мгновенная мощность не содержит постоянной составляющей, так

что

0, .PSUIQ





Индуктивность и емкость – накопители энергии, а не потребители,

поэтому их называют реактивными элементами.

Последовательное соединение элементов R, L, C

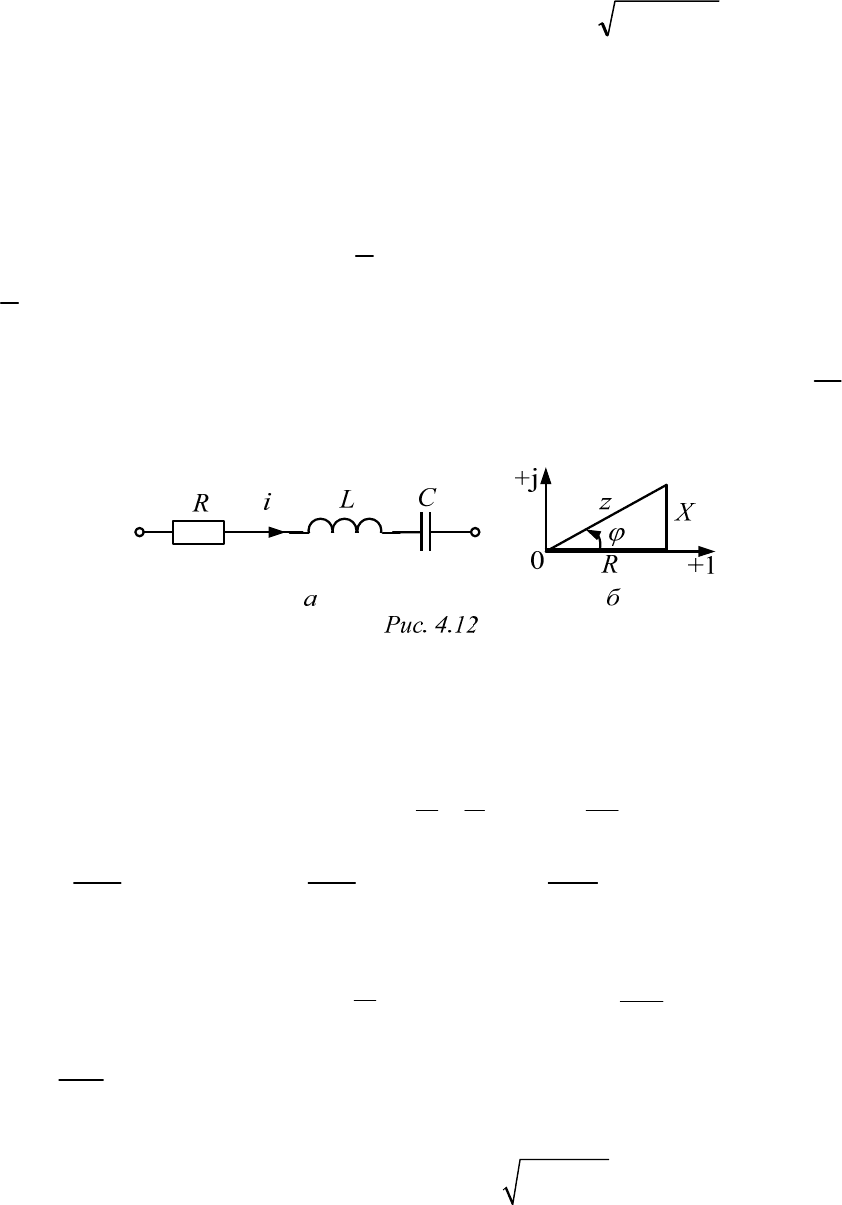
По второму закону Кирхгофа для схемы рис. 4.12, а найдем

sin( ) cos( )

LC m i Lm i

u u u u Ri L idt RI t X I t

dt C

 

      



cos( ) [ sin( ) cos( )],

Cm i m i i

XI t I R t X t







где величина

XX X





называется реактивным сопротивлением.

Если построить прямоугольный треугольник с катетами

cosRz





sin ,

XX X z





то его гипотенуза





называется

полным сопротивлением. Этот треугольник носит название треугольни-

ка сопротивлений. Тогда

sin( ) sin( ).

mimu

uIz t U t



 



И вновь справедлив закон Ома для амплитуд и действующих зна-

чений тока и напряжения:

.; zIUzIU









Он может быть записан

и для их комплексов:

,UIZ



где коэффициент пропорциональности

jZR Xze



  

комплексное сопротивление. Для иллюстрации по-

следнего выражения достаточно треугольник сопротивлений поместить

на комплексную плоскость (рис. 4.12, б). При этом угол

arctg





треугольнике равен углу сдвига фаз напряжения и тока.

Параллельное соединение элементов R, L, C

По первому закону Кирхгофа для схемы рис. 4.13, а, считая задан-

ным напряжение, найдем ток







Cudt

iiii

CLR

sin( ) cos( ) cos( )

mm m

uuu

UU U

ttt

RX X

  

  

[sin( ) cos( )].

mu u

Ug t b t







Здесь обозначены:





активная,





индуктивная,



емкостная,

bb b

реактивная проводимости. После

построения треугольника проводимостей (рис. 4.13, б) с катетами g и b

и введения в расчет его гипотенузы

,ygb

которая называется

полной проводимостью, окажется

sin( ) sin( ).

mumi

iUy t I t



 



 

Закон Ома в этом случае приобретает такие формы:

;; ,

UyIUyIUY  



где комплексная проводимость

-j

j,Yg bye



 

что становится оче-

видным, если треугольник проводимостей поместить на комплексную

плоскость (на рис. 4.13, б при





треугольник располагается в чет-

вертом квадранте). При этом угол

arctg





в треугольнике равен углу

сдвига фаз напряжения и тока.

4.6. Две схемы замещения пассивного двухполюсника

Если на векторной диаграмме (рис. 4.14, а), где изображены векто-

ры тока и напряжения пассивного двухполюсника, спроектировать век-

тор напряжения на вектор тока и направление перпендикулярное ему, то

полученные проекции называются активной

cos





и реактивной

sin





составляющими напряжения. При этом образуется тре-

угольник напряжений, который показан пунктиром. Разделив его катеты

на действующее значение тока, получим параметры последовательной

схемы замещения двухполюсника (рис. 4.14, б):





если ток отстает от напряжения.

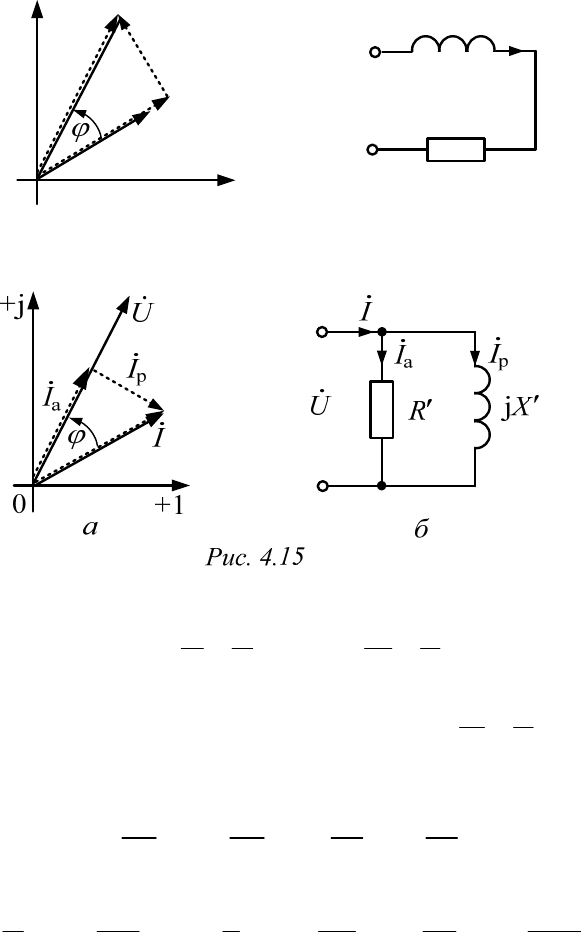
Если же вектор тока спроектировать на вектор напряжения и

направление перпендикулярное к нему (рис. 4.15, а), то проекции назы-

ваются активной и реактивной составляющими тока (

). При этом

получится треугольник токов (выделен пунктиром).

В свою очередь,

;





это параметры параллельной

схемы замещения (рис. 4.15, б).

Рис. 4.14

Сравнивая треугольники сопротивлений и проводимостей, найдем:

cos ; sin .



  

Учитывая, что по закону Ома должно быть



получим со-

отношения:

2222

;;;;

bRX

RXgb

yyzz



222

;; .

XRXR

RR XXL L

gR bX







   

При анализе работы конкретного пассивного двухполюсного

устройства можно выбирать либо последовательную, либо параллель-

ную схему замещения.

Из подобия треугольников напряжений, сопротивлений, проводи-

мостей, токов и мощностей следуют соотношения:

;;

gUUIRIIUPyUzIUIS 

bUUIXIIUQ 

4.7. Основы комплексного метода

Комплексный (символический) метод использует замену операций с

синусоидальными функциями времени действиями над изображающими

их комплексными числами и базируется на следующих ниже теоремах.

Пусть мгновенному значению тока





2sin( ) Im 2

iI t I e



















соответствует комплексное действующее значение

IIe







тогда легко доказать подстановкой нижеследующие положения.

Теорема линейности: линейной комбинации синусоид соответ-

ствует такая же комбинация изображающих их комплексов

() .

kk k k

it AI





Иными словами, сумме синусоид соответствует сумма изобража-

ющих их комплексов, умножению синусоиды на постоянное число –

умножение комплекса на то же самое число.

Теорема дифференцирования: операции дифференцирования сину-

соиды по времени соответствует умножение изображающего ее ком-

плекса на j



, т. е.







Теорема интегрирования: операции интегрирования синусоиды по

времени соответствует деление изображающего ее комплекса на



т. е.

idt









4.8. Законы Ома и Кирхгофа в комплексной форме

В соответствии со свойством линейности законы Кирхгофа приме-

нительно к синусоидальному режиму работы цепи можно переписать в

комплексной форме следующим образом.

Первый закон. Алгебраическая сумма комплексных токов в узле

равна нулю.

Второй закон. Алгебраическая сумма комплексных падений

напряжения в контуре равна алгебраической сумме комплексных ЭДС.

Или: для узла

0;I 





для контура

,UE





причем в понятие «алгебраическая» вкладывается тот же смысл, что и

для мгновенных значений величин.

Закон Ома в комплексной форме получается в результате примене-

ния всех вышеприведенных теорем к последовательному и параллель-

ному соединению элементов R, L, C (фактически он уже получен выше

без строгих доказательств):

, или , такUIZ IUY  

 

что 1, гдеZY





Отсюда легко получаются формулы для определения параметров

двух эквивалентных схем замещения пассивного двухполюсника.

Добавим к этим формулам понятие комплексной мощности

€

.SUI







Если

UUe IIe







то сопряженный комплекс тока

€

IIe







тогда

cos j sin j .

SUe Ie Se S S P Q













Сравнивая приведенные в этом разделе формулы с формулами,

связывающими постоянные токи, напряжения и мощности, увидим, что

они отличаются лишь обозначениями (табл. 4.1).

Таблица 4.1

Постоянный ток Синусоидальный ток

Для узла











Для контура





UE





Для пассивного

двухполюсника

U = IR

RG = 1

UIZ











Мощность

PUI IR



€

SUI I Z



 



Следовательно, все методы расчета, основанные на законах

Кирхгофа и используемые для расчета цепей постоянного тока, приме-

нимы и к расчету цепей синусоидального тока в комплексной форме.

j, j .ZR Xze Yg bye





   

5. ЦЕПИ С ИНДУКТИВНО СВЯЗАННЫМИ ЭЛЕМЕНТАМИ

5.1. Основные понятия и определения

Если при изменении тока в одном элементе цепи в другом возника-

ет ЭДС, то такие элементы называются индуктивно связанными, а наве-

денная ЭДС носит название ЭДС взаимной индукции.

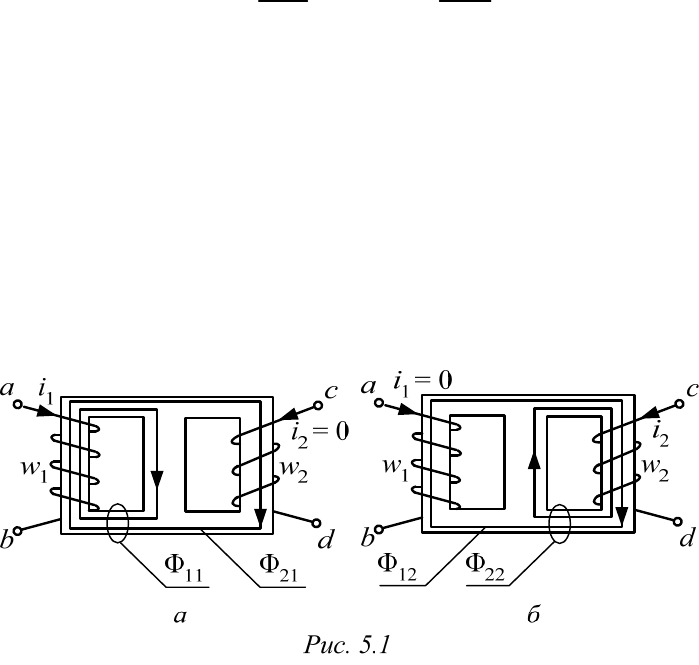
Рассмотрим две обмотки, находящиеся на крайних стержнях нена-

сыщенного магнитопровода (рис. 5.1, а). Пусть

0,i



тогда магнитные

потоки самоиндукции



и взаимоиндукции



окажутся пропорцио-

нальными току

равно как и потокосцепления соответствующих об-

моток с потоками, их пронизывающими,

11 1 11 21 2 21

и .ww  

Коэффициенты пропорциональности

носят названия собственной индуктивности первой обмотки и взаим-

ной индуктивности второй обмотки по отношению к первой (прилага-

тельное «собственная» обычно опускают).

Разумеется, при

0i 

и наличии тока

(рис. 5.1, б) магнитные по-

токи само- и взаимоиндукции

22 12

( и )



и соответствующие пото-

косцепления будут пропорциональны этому току:

Здесь

L 

(собственная) индуктивность второй обмотки, а



взаимная индуктивность первой обмотки по отношению ко второй.

В линейных цепях справедлив принцип взаимности, поэтому

12 21



и говорят просто о взаимной индуктивности двух обмоток М.

При наличии обоих токов (рис. 5.2, а) по принципу наложения

11 21

121

иLM





22 2 22 2 2 12 1 12 12 2

и .wLi wMi 

1222122221112111

MiiLMiiL 





















Если изменить направление одного из токов или иначе намотать

одну из обмоток, то изменятся знаки перед потокосцеплениями взаим-

ной индукции. Для облегчения решения вопроса об этих знаках вводит-

ся понятие одноименных зажимов.

Два зажима, принадлежащие двум разным индуктивно связанным

элементам, называются одноименными и помечаются одинаковыми

значками (звездочками

* или точками ), если при одинаковой ориента-

ции токов по отношению к этим зажимам потоки само- и взаимоин-

дукции складываются.

Согласно этому определению на рис. 5.2, а одноименными являют-

ся зажимы b и d, помеченные (*), а также зажимы a и c. Теперь нет нуж-

ды изображать магнитопровод, поэтому на схеме индуктивно связанные

элементы обозначаются, как показано на рис. 5,2, б.

Степень индуктивной связи оценивается коэффициентом связи



Нетрудно убедиться, что значение

не может превышать 1.



Если токи изменяются во времени, то в индуктивно связанных эле-

ментах, наряду с ЭДС самоиндукции, возникают и электродвижущие

силы взаимной индукции

12 2 21 1

ddi ddi

eMe M

dt dt dt dt



   

которые компенсируются соответствующими напряжениями

Поэтому падение напряжения на каждом из элементов складывает-

ся из двух составляющих:

11 1 1

;

di di

uu u L M

dt dt

  

2222

Luuu



В комплексной форме

11 1 11 2

jj;

ML M

UU U XI XI  

   

22 2 22 1

jj,

ML M

UU U XI XI  

   

где





сопротивление взаимной индукции,

XZ

ком-

плексное сопротивление взаимной индукции. Эта величина обозначает-

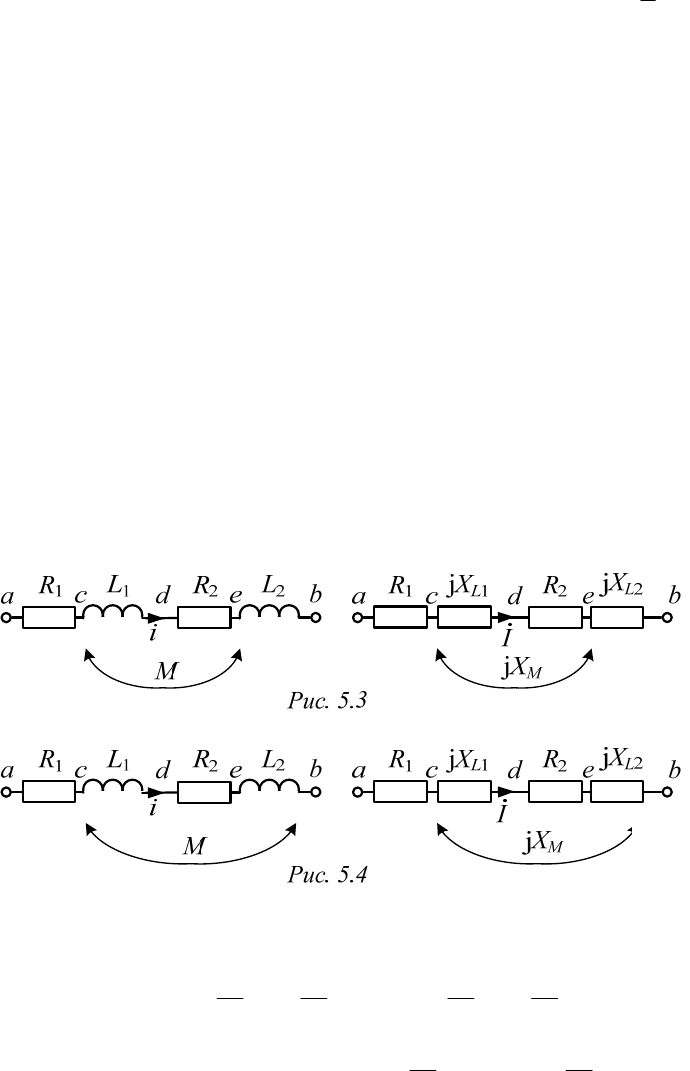
ся на комплексных схемах с индуктивной связью (рис. 5.3, б и 5.4, б).

При составлении уравнений второго закона Кирхгофа для цепей с

индуктивной связью нужно учитывать

правило знаков для напряже-

ний само- и взаимоиндукции

: если токи ориентированы одинаково по

отношению к одноименным зажимам, то знаки этих напряжений

должны быть одинаковы, если ориентация различна, то и знаки про-

тивоположны.

5.2. Последовательное соединение

индуктивно связанных элементов

Рассмотрим последовательное соединение двух катушек, индук-

тивно связанных между собой. Возможны два случая: ток ориентирован

одинаково по отношению к одноименным зажимам катушек (такое

включение называется согласным – схемы на рис. 5.3, а, б) и по-разному

(это встречное включение – схемы на рис. 5.4, а, б).



Найдем параметры эквивалентного двухполюсника. По второму за-

кону Кирхгофа для схем, показанных на рис. 5.3, а и 5.4, а,



LiR

LiRu

2211

,)2()(

2121

LiR

MLLiRR

ЭЭ



где

,2,

2121

MLLLRRR

ЭЭ





знак «плюс» соответствует соглас-

ному включению, «минус» – встречному.

Для комплексных схем (рис. 5.3, б и 5.4, б)

11 2 2

jj j j

MLM

URIXIXIRIXIXI     

    

12 1 2

j( 2 ) ( j ) ,

LM ЭЭ

RXX XIRXI     



11 2 2

где ;;;

LL M

XLX LXM







в свою очередь,

.;2

21Э21Э

RRRXXXX

MLL









Таким образом, за счет индуктивной связи эквивалентные индук-

тивность, индуктивное сопротивление, а значит и полное сопротивление

ветви увеличиваются при согласном включении и уменьшаются при

встречном. Отсюда вытекает способ экспериментального определения

одноименных зажимов катушек.

Если при одном значении напряжения и различном включении

элементов измерить токи, то в том случае, где ток

больше, включение

встречное и катушки соединены друг с другом одноименными зажима-

ми. Если же при одном токе и различном включении элементов изме-

рить напряжение, то оно будет больше при согласном включении.

Убедимся в этом на примере 5.1.

Пример 5.1

Построить векторные диаграммы цепи с последовательным со-

единением индуктивно связанных катушек при их согласном (рис. 5.3) и

встречном (рис. 5.4) включении. Найти напряжения на каждом из эле-

ментов и на входе цепи.

Дано: в обеих схемах

1A; 20Ом.

IRX





30 Ом;50Ом.

RX X 

Решение

Вычислим напряжения на активных сопротивлениях, а также

напряжения само- и взаимоиндукции каждого из индуктивно связанных

элементов.

20 B; 50 B; 30 B;

ac cc L c d M

UIR U IX U IX



    

30 B; 20 B; 30 B.

de ee L f b M

UIR U IX U IX



    

Точки



на схеме отсутствуют. На диаграмме они будут раз-

делять векторы напряжений само- и взаимоиндукции.

Построим топографические диаграммы напряжений (рис. 5.5, а, б).

Напомним, что падения напряжения на активных сопротивлениях

совпадают по фазе с током, напряжения самоиндукции опережают ток

на 90 градусов, а напряжения взаимной индукции либо отстают от тока

на тот же

угол (встречное включение – рис. 5.5, б), либо его опережают

(согласное включение – рис. 5.5, а).