Фрумкин А.Н., Багоцкий В.С., Иофа З.А., Кабанов Б.Н. Кинетика электродных процессов

Подождите немного. Документ загружается.

}равнение

(39)

позволяет определить'

если

9делать

простейшлие

допущения

о зависимости заряда от адсорбированного количества г,

как

и3мет{яется

величиной

концентрацр1я

с'

соответствующая постоян-

ному адсор6ированному количеств} |, т.

е. как изменяется адсорбируемость

вещества с потенциалом. 1аким путем

мох(но вь|вести следующее

соот_

но1пение:

'':

(ч"

2ч,)]

(40)

Беличины

со

с9о обозначатот 3десь концентрации' соответствующие

одной

и той х<е величине

адсор6ции

при потенциале

нулевого заряда и

при

потенциале' отличающемся от

последнего

на величин!

9"1

€-емкость

двойного

слоя в исходном

растворе

электролита' которая

считается

по-

стоянной,

(,'-3уц691ь

двойного

слоя при

3аполнении

поверхности

адсор-

бированньтми молекулами'

9в-€Авиг

потенциала

нулевого

заряда

пр;4

заполнении

поверхности

3-площадь,

покрь1ваемая

одним молем

адсор-

бированного вещества в

условиях

3аполнения.

|1ри

помощи

уравнения

({0)

мо)кно

удовлетворительном

согласии

опь1том

определить

форму

электрокапиллярнь1х кривь1х' получаемь1х

растворами'

содер)кащими

адсорбирующиеся вещества. 1ак

как согласно

вь!1песка3анному

€

6|,

то

при

достагочно

больтших

знак

правой

части

уравнения

(40)

всегда полох{ительньтй;

иначе

говоря'

при

достаточно

боль-

1пом

удалении

от нулевой

точки концентрация

адсорбирующегося

веще-

ства'

соответствующая

определенному значени}о адсор6ции, во3растает

дальнейтпим

удалением.

Фтсюда

следует'

что

при постоянной концентра-

ции

величина

адсорбции

убьтвает

ростом

как это и наблходается

на опь:те*

Более

детальньтй

анал'1з этих соотно:пений

приводит

к вь1воду' что

на

границах области

адсорбт{ии и3менение адсорбированного

количества с

потенциалом

дол)кно

бьтть очень

резко

вь1рах{ено' как

это видно из

рис'

1акой ход и3менения

адсорбции

потенциалом

дол>кен

привести к по_

явленито максимумов'на кривой

зависимости

дифференциальной

емкости

от

потенциала.

Аействитель1'о'

обозначим

дол1о

поверхности'

занятой ор-

ганическими

молекулами' чере3

(0:

|5)

предполол{им

Аля

простоть1'

нто адсорбция

органических молекул не сдвигает нулевой точки.

3аряд

поверхности

мо){<но

приблих<енно

вь]ра3ить' как сумму зарядов части

по-

верхности

свободной

от

адсорбированнь!х

молёкул, и части

поверх-

ности

ими занятой:

о:€ч'(1_0)

*€'Р'0-

(41)

йз

уравненпя

(4\)

получаем

для дифференциальнот]

емкости

вь|ра-

)кение

с":#:

о)

,',

_#'(€_с')

ч".

(42)

|[ервые

два

члена

правой

части

уравнения

(42)

дают

3начения

емко-

сти'

лех(ащие

ме'{ду величинами

емкости

при

0:0-..и 0:1,

т. е. €

€'.

1ретий

член свя3ь1вает

диференциальную

емкость

3ависимостью ад-

сорбции

[

от

потенциала.

1(ак

легко

уФдиться,

на границах области

адсор6шии

он имеет всегда

полох{ительное

3начение.,[,ействительно,

рассмотрим'

например' левую

границу

о6ласти адсорбшии на

рис.

27.

Бысокомолекулярнь|е

органические

катионы' как'

например'

ион

ш(с4н9);'

ведут

себя частично, как ионы' частично' как молекулы' хотя

они и

адсорбируются

преимущественно

на

отрицательно заря)кенной поверхност14; лР|| очень больтпих

значеп:иЁх

отрицательного

заряда

наступает их

десорбция.

этом

случае

возрастает

при

убьтванъ1|1

9@'

так

9о:9_9,

)

0 и,

следовате.,1ьно'

)

Ф;

далее,

сс_6') 9'

о9\

Ёа гранипах

области

адсорб4ии,

всдедс-твие

резкого

изменения

адсорб-

циис

потенциалом;

аФолютная

величи"'$

"''.,о

во3растает'

вслед-

ствие

чего на

кривой зависимост"

}

появляются

ре3кие

максимумь|.

в то время как и3мерение

электрокапиллярнь1х

кривь1х

возмо'(но

только

в случае

жидких

металлов'

метод

измерения

емкости

имеет

более

1пирокую

область

применения.

1,1змерения

диференциальной

емкости

различнь1х

твердь|х металлов'

например'

сви!{ца'

кадмия

олова

раство_

рах'

содер>кащих

адсорбирующиесядо6аьки,

пока3али'

что

в'этих

слу-

чаях адсорбция

происходит

только

в определенном

интервале

потенциа-

лов в6лизп нулевой

точки

данного

металла[36].

Бнутри

этого

интеРвала

3начения

диференциальной

емкости

пони)кень|, а на

границе

проходят

через максимум.

в.

АдсоРБция

Атомов

водоРодА

Ёаряду

с адсорбцией

ионов

и молекул

на электро-химические

свой-

ства

поверхности

металлов

сильно

влияет

так}ке

адсорбшия

атомов водо:

рода

кислорода,

в некоторь1х

случаях

других

элементов.

йзвестно,

нто

многие

металль|'

особенно

металльт

платиновой

группь1'

а в

определеннь|х

условиях

и никель'

в вьтсокой

степени

обладают стособ-

ностьто

адсорбироьать

водород.

Физипеская

адсорбция

водорода

(т.

е.

адсорбция

за

счет сил мех(думолекулярного

в3аимодействия)

при

обын_

нь1х

температурах

исчеза[още

мала.

Б химическом

отно1пении

молекула

водорода

является

вполне

нась1щенной,

поэтому заметная

адсорбшия

водорода

указь1вает

на

распад

молекулы

водород3

процессе

адсорбт:.ии

на

химически ненасьтщенньте

свободнь]е

атомь].

Ёаличие

такого

распада

вь|текает

так}ке

из

параллелизма'

существующего-ме)<ду

явлениями

ад_

сорбции

водорода

растворения

его

в металлах.

(ак

вь1текает из опь|та'

при

маль|х

концентрациях

растворенного

водорода

количество водорода

в металле

пропорционально

корн}о

квадратцому

и3

концентрации

его

газовой

фазе.

Фтсюда

следует'

что

водород

растворен

в металле

не в виде

молейул'

виде

атомов-

}тот

вывод мох(ет

бьтть

перенесен и на

слунай

адсорбции

водорода.

\ак

как теплота

диссоциации

молекуль1

водорода

равна

\02 ккал

на моль'

то полох(ительное

значение

теплоть1

адсорбции

водорода

во3мо)кно

только

том случае,'если

теплота

адсорбции

атомарного

водорода

на

металле

превьт1пает

половину

этой

величинь|'

т. е. 5\

ккал на грамм-

атом. такйм

образом,

3аметная

адсорбция

водорода

мох(ет наблюдаться

только на'металлах'

обладающих

значительнь|м

сродством

атому

водорода.

€пособность

металлов

адсорбировать

водород

сохраняется

и в

присут-

ствии

растворов

электролитов.

этом

случае

для

исследования

свойств

.во.(о!о.(а;

адсорбированного

на

поверхности

металлического-

электрода'

как

йоказали

рабо+ь'

А. н. Фрумкйна,

и.

|[[ль:гина

Р^. Р..

3рш:лера,

мох(ет

бьтть

с'успехом

применен

метод

кривых

3аря>кения[8'

14' 15].

€огласно

для

использования

этого

метода

необходимо

исключить

во3мо'(ность

протекания

электрохимических

реакции

3а

счет веществ'

а0

9[Ф--

оч

содер)кащихся

объеме

раствора.

Ёсли сообщать

платиновому электроду'

находящемуся

равновесии

раствором'

нась1щенным

водородом

под

атмосфрньтм

давлением'

поло'(ительные

заряды'

то

растворенньтй

моле_

кулярный водород

переходит

состояние ионов'

и чере3 элек'трод

идет

ток.

Б этих

условиях

снятие

кривой

заря}кения

невозмо)кно.

ЁетруАно;

однако' осуществить

такие

условия,

при которь|х количество

растворен-

ного

водорода

бь;ло бы

мало

по сравнению

количеством

адсорбирован-

ного. Ёаряду

увеличением

поверхности

электрода

умень11]ением

объ_

ема

раствора

(см.

4), это

,{Фё[[[аёт€.я

так)ке

сни)кением

концентрации

водорода'

растворенного

в электроли-

те.

(ак

булет

показано

ни){{е'

коли-

чество

водорода' адсорбированного

на электроде'

умень!пается

при по-

них(ени.и его концентрации

в объеме

'гора3до

медленнее,

чем

количество

водорода в

растворе'

€

(Ф1Ф|Б|й

3.[ё:

ктрод

находится

.в

равновесии.

|1о-

этому

перед снятием кривои

заря>ке-

ния

целесообразно

удалить

больтшую

часть

растворенного

в электролите

-водорода'

например' пропуская

че-

рез

него азот. ||ри

этом с электро-

да

снимается сравнительно

неболь-

|11ая

часть

адсорбированного

водо-

рода.

€ообщая электроду

после этого

возрастающие количества электриче-

а#'

(н.в.3.)

0,6

0,4

0,2

0,25

0,5

мцлл|]кцл0нё!

ства

мь| получим кривую зарях(е-

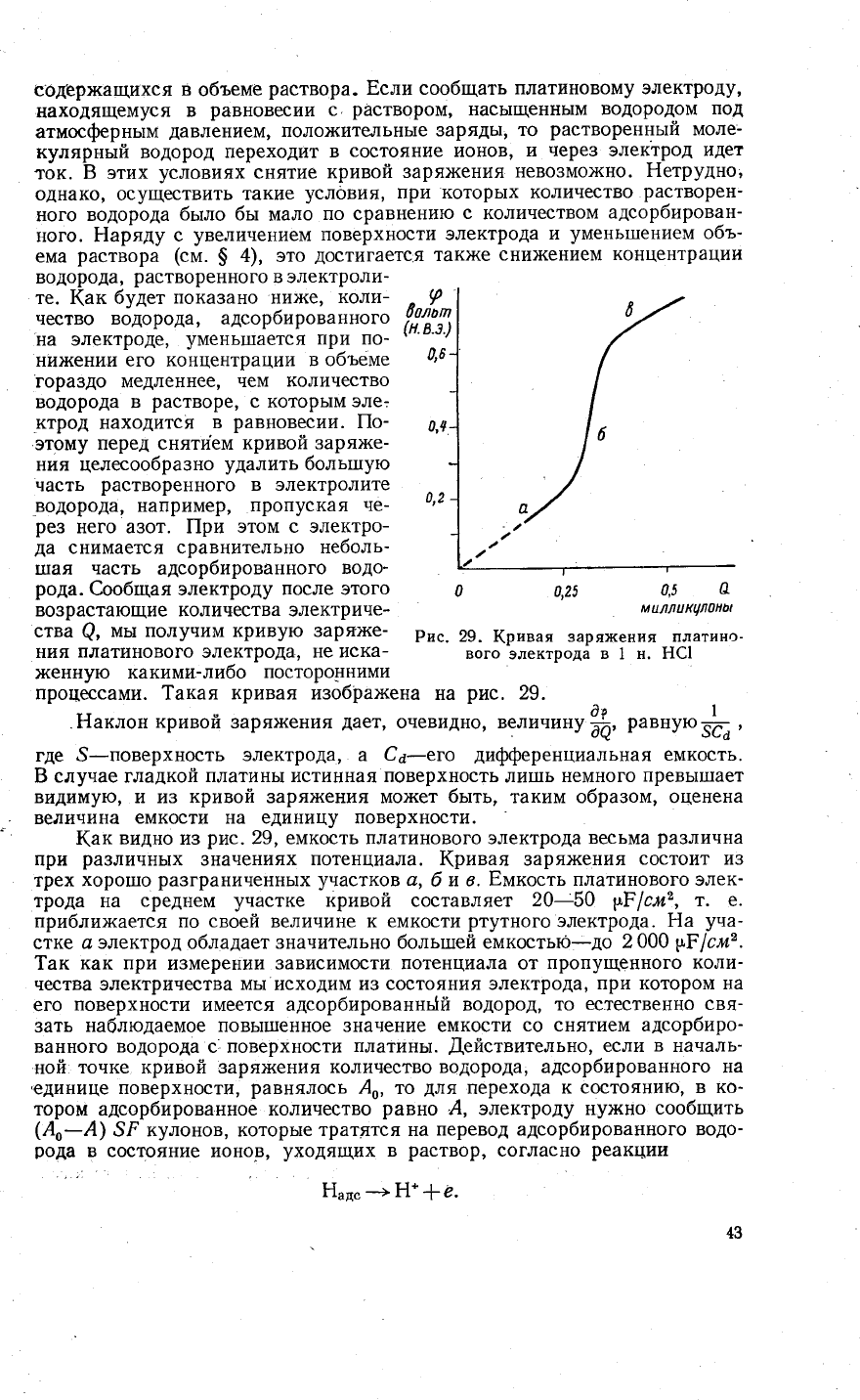
Рис.

29. 1(ривая зарях<ения платино-

ния

платинового

электрода, не

иска-

вого

9лектрода

н. Ё€1

)кенную

какимп-либо

посторонними

процессами.

1акая

кривая изобрах<ена

на

рис.

29.

.Ёаклон

кривой

3арях(ения

дает'

очевидно' велич^"х%,

р'",уто5|

где 3-поверхность

электрода, а

64-его

диференшиаль|1ая

емкость.

3 слунае гладкой

платинь1 истинная поверхность

ли1пь

немного

превь1|пает

видимую' и из кривой зарях<ения мо}кет

бьтть,

таким образом, оценена

величина

емкости на единицу поверхности.

(ак

видно из

рис.

29, емкость платинового электрода

весьма

различна

пр|{

различнь]х

значениях

потенциала. 1(ривая

3аря)кения

состоит из

трех

хоро1по

разграниченнь1х

участков

а,

и с.

Бмкость платинового элек-

трода на

среднем

участке

кривой составляет

20---:50

рР!см2,

т. е.

прибли>кается по своей

величине

к емкости

ртутного

электрода.

[1а

уна-

стке

а электрод

обладает

значительно больтпей емкостьЁ-до

000

рР|см2.

1ак

как при

измерени\4 завис|1мости

потенциала

от

пропущенного коли-

чества электричества

мь|

исходим

и3 состояния электрода'

при котором на

его

поверхности

имеется адсорбированнь1й водород,

то

естественно свя-

зать

наблюдаемое повь]1пенное значение емкости

со снятием адсорбиро-

ванного

водорода

с поверхности

платиньт.

Аействительно'

если

началь_

ной

точке кривой зарях{ения

количество водорода' адсорбированного на

'единице

поверхности,

равняло|Б

А1, то

для

перехода

к состоянию'

в ко-

тором

адсорбированное

количество

равно

.А,

электроду ну)|(но

сообщить

@,_А)

5Р кулонов, которь1е

тратятся на

перевод адсорбированного водо-

рода

в состояние

ионов,

уходящих

раствор'

согласно

реакции

Ёад"

А"

+е.

}то количество

электричества

складь1вается с тем'

которое

идет

1{а

зарях{ение

двойного

слоя и

которое' очевидно'

равно

(е_е.)

где 3начения

плотност1'! 3аряда

€0

относятся

к начальному и конечному

состоянию электрода.

1аким

образом, мех<ду количеством

электричества

.(,

сообщеннь]м

электроду'

и3менением

адсорбированного

количества

во-

дорода

и зарядом

поверхности

должно

существовать

соотно1пение

9=(А,_А)5л{(е_е')5

14ли в

диференциальной

форме:

А0:

-^,4.5л}Ае.5.

1ак

как на

участке

б кривой 3аря)кения

емкость

электрода

имеет,

как

уже

бьтло

указано'

3начен\4е,

6лизкое

к обьтчной величине

емкости

двоййого

слоя' то

адсорбция

водорода

в этой

о6ласти

очевидно мала,

первьтй

член

правой

части

уравнения

(43а)

не

влияет существенно

на

ве_

линйну

А( (двойнослойная область кривой

заря>кения*).

!!4наче

обстоит

дело

на

участке

а кривой заря'{ения.

14з

сильно повь1_

1пенного 3начения

емкости

следует'

что в этом

случае

величина-^А

велика

по сравнению

Ае.

3 первом приблих<ении мо}кно

да)ке

считать'

что

практически

все сообщенное

электроду

количество электричества

тратится

на

снятие

адсорбированного

водорода' и

поэтому мо)кно опреде-

лить величину

А,-А из

1ак

как в

конце

участка

авеличина.4 обращается

в нуль или

делается

очень

малой,

то таким

путем мох{но

найти и 3начение

для

лтобой точки

этого

участка

кривой заря)кения.

3то

определение

мо)кно

уточнить'

оце_

нив

величину

о-е0

по наклону

кривой 3арях{ения

двойнослойной

области

или определив

ее

другим

путем

(например'

и3 3ависимости

адсорбции ионов'

связанной

образованием

внетпней

о6кладки

двойного

слоя' от потен-

|7иала'

как это бьтло

разъяснено

4).

|!роцесс

снятия адсорбированного

водорода

обратим.

!,ействительно,

если

какой-нибудь

точке

участка

а или б

кривой

3аря)кения

(рутс.

29)

переменить направление

пропускаемого

тока'

то

мо'(но

пройти кривую

заря)кения

в обратном

направлении.

Фпьтт показь|вает' что

получаемая

при этом

(катодная)

кривая заря)кения

почти совпадает

с <анодной>

кривой, при

снятии которой

значения

потенциала изменялись

от более

отрицательньтх

более поло)кительньтм.

}}4з обратимости

кривой

заря>ке_

ния следует' что

состояния'

через

которь1е проходит

электрод

при снятии

кривой зарях(ения'

мох{но

достаточньтм

приблих(ением

рассматривать'

как

равновеснь]е.

]аким

путем мо)кно

установить

равновесную

зави-

симость

мех{ду

потенциалом электрода

количеством адсорбирован_

ного

водорода

А.

|4з

лри6ли3ительно

прямолинейного

хода кривой заря>кения

следует'

что эта зависимость

так)ке является

линейной:

{44'

йз

уравнения

(44)

легко

получить адсорбционну1о

и3отерму

водорода

на

поверхности электрода.

.(ействительно,

величина

мох(ет

бь:ть

вь1рах(ена

по

формуле

Ёернста через

парциальное

давление

молекуляр-

(43)

$3а|

что

некоторь|е' хотя

отно-

остаются

на

поверхности

Более

детальное

рассмотрение

пока3ь|вает'

однако'

сительно

небольп:ие'

количества адсорбированных

га3ов'

электрода

двойнослойной

области.

ного

водорода, находящегося в

рав1{овесии

элект!о.{ом

!ц2:

-.^о

д7

у-у

1лРн"

где90*3начение9вданном

растворе

лРи

Рна:|

аптм.

|1одставляя

это

вь1-

А:а'{0'1лр1',

(Аа)

!де

а'

у*

0'_постоя[{нь|е.

Рассмотрение

кривой заря>*{ения

показь1вает'

что логарифминеская 3ависимость вь1полняется

в 1пироком интервале

изменения Б9.п!т!|4нь1

/)112.

Ёаличие

такой

зависимости требует

специального

объяснения. ||ри

адсорбции

двухатомного

газа, сопрово)кдающейся

диссоциацией

на атомь1'

на однородной

поверхности в отсутствие

сил в3аимодействия ме)кду

адсор-

бированньтми атомами

адсорбционная

изотерма

определяется следующим

соотно|пением

(уравнение

.[{энгмюра):

'{Б

|*.|

Рня

(45)

где,4-_предельное

значение адсорбшии

при

заполнении

поверхности'

Ф-

постоянная.

|!ри

маль|х заполнениях

это

соотно1']]ение вь1рах{ает пропор-

циональность

мех(ду

и корнем

квадратнБ\\| ||3

'|н2.

Ёаблюдаемая

на опь1те логарифмическая и3отерма

существенно

отли-

чается от

изотермь1'

вь|веденной на основании

приведеннь1х вьт|ше про-

сть|х

допущенйй,

а именно

она

дает

гора3до более

медленное во3растание

величинь1

р,'.

1акое медленное

во3растание

пока3ь1вает, что

дифе-

ренциальная

работа

адсорбции

убьтвает

по мере заполнения

поверхности.

йзменение

работьт

адсорбции

мох<ет бьтть вьтзвано' например' неоднород-

ностью

поверхности.

Ёа неоднородной

поверхности

при

маль]х

давлениях

адсорбирующегося

газа заполняются

более активнь|е

участки

поверх-

ности' а

лри боль:пих-менее активнь1е.

Бследствие этого

работа

адсорб-

ции

постепенно

убьтвает

увеличением

степени

3аполнения'

}казанньте вопрось1

бьтли подробно

рассмотрень|

советскими

физико-

химиками

€.

3. Рогинским

|37]

и, особеЁно в

применении

к электрохимии'

.]!1.

1,1.

1емкинь|м

[38].

!,ругой

прининой

убьтвания

работьт

адсорбции мо)кет

бьтть наличие отталкивательнь]х

сил ме>*{ду адсорбированнь1ми

атомами

[39].

0ба

эти

представле|1ия при

определеннь1х

допущениях

приводят к логариф-

мической и3отерме адсор6ции.

3аметим,

что

аналогичная

логарифмине-

ская

3ависимость

ме}кду количеством

поглощенного

водорода

и его

дав-

лением наблюдается и

т1ри

растворении

водорода в некоторь1х металлах'

хоро1по

растворяющих

водород'

например'

ъ лалладии, если

только

концентрация

растворенного

водорода в металле

достаточно

велика

(так

назь]ваемая область

$-фаз

в системе

Р6-н). 3то приводит нас

вь]воду'

что

процесс

адсорбции

водорода в

и3учаемь!х

условиях

мох{но

рассмат-

ривать

как

растворение

водорода' ограничива}ощееся

поверхностнь1м

слоем

ц612дд2

[8.!.

|4змерение

кривых заря)кения

позволяет

обнарух<ить

и некоторь1е

дру-

гие интересньте

свойства

адсорбированного

водорода' в

частности' зависи-

мость энергии свя3и металл/водород

от

природь1

электролита.

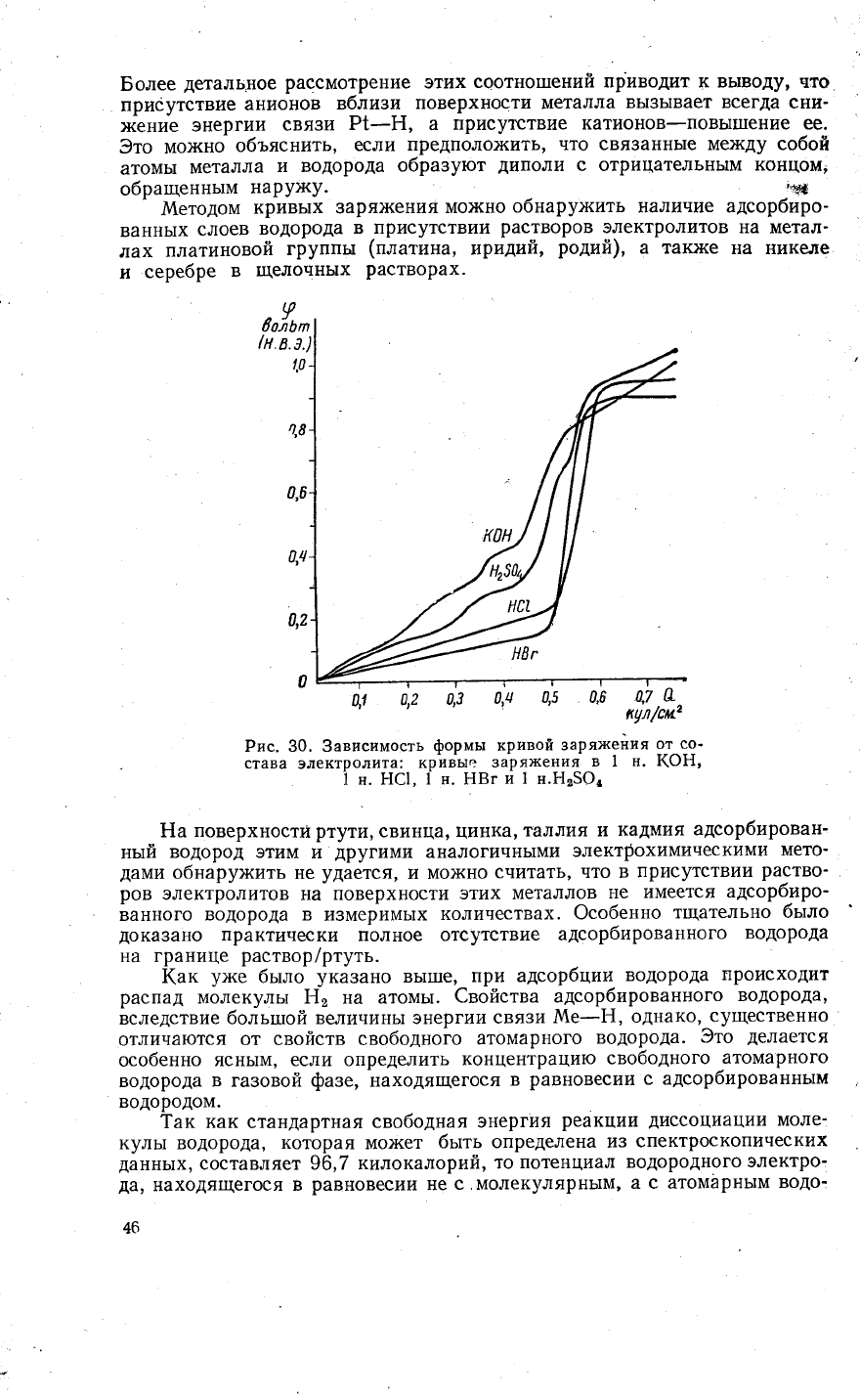
(ак

видно

из

рис.

30,

на

котором

приведень| кривь1е

заря)кения

платинированного

платинового электрода в

растворах

1(ФЁ, н25о4, Ё€|

и ЁБг, адсорбиро-

ванньтй

водород снимается

с поверхности при значительно

менее

поло-

)|(ительнь1х потенциалах в Ё8г, чем' напри]у1еР,

в Ё'5Фд.и особенно в

кон.

Более

деталь$ое

рассмотрение

этих

соотно!шений

приводит к вь|воду'

что

приёутствие

анионов

в6лизуу,

поверхности металла

вь]зывает

всегда

сни_

х<ение

энергии

связи

Р1_н,

присутствие

катионов-повы|пение ее.

3то мо>кно

объяснить,

если

предполо)кить'

что связаннь1е ме)кду собой

атомь|

металла

и водорода

образуют

дит|оли

с отрицательным

кФЁ|],Фй;

обращенньтм

нарух(у.

::.**

.|[етодом

кривь1х

заря}кения

мох(но

обнару>кить наличие адсорбиро-

ванных

слоев

водорода

в присутствии

растворов

электролитов на

метал_

лах

ллат||новой

группы

(платина,

придий,

ролий),

а так}ке

на никепе

серебре

щелочных

растворах.

8'уь'

/н.в.э.)

1.0

0'6

!'7

хцл/см2

Рис. 30. 3ависимость

формы

кривой

заряя,ейия

о'-со'

става

электрол"Ё1',?}1Ё";?1т':?{Ё'в

н'

1(ФЁ'

$а

поверхности

ртути'

свинца'

цинка'

таллия

кадм!4я

адсорбирован-

ньтй

водород этим

другими

аналогичными

элект!охимическими

мето_

дами

обнару}кить не

удается'

и мох(но

считать,

что в

присутствии

раство_

ров

электролитов

на

поверхности

этих металлов

не

имеется адсорбиро_

ванного

водорода в

и3меримьтх

количествах.

Фсобенно

тщательно

6ьтло

доказано

практически

полное

отсутствие

адсорбированного

водорода

на границе

раствор/ртуть.

1(ак

ух<е

бьтло

указано

вьт1ше'

при адсорбции

водорода

происходит

распад

молекуль1 Ё,

на

атомь1.

€войства адсорбированного

водорода'

вследствие больт'пой

величинь1 энергии

связи

.&1е-Ё,

однако,

существенно

отличаются

от свойств свободного

атомарного

водорода.

3то

делается

особенно

яснь1м' если определить

концентрацию

свободного

атомарного

водорода

газовой

фазе,

находящегося

равновесии

с адсорбированньтм

водородом.

1ак

как

стандартная

сво6одная

энергия

реакции

диссоциаци1:1

йФ.)]€-

куль1 водорода'

которая

мо)кет

бьтть определена

из

спектроскопических

даннь]х'

составляет 96,7 килокалорий,

то

потенциал водороднФгФ

9/1€кт!Ф:

да'

находящегося

равновесии

не

с.молекулярнь1м'

а с атомар}{Б]й

вФАФ:

0,5

0,4

0,3

0,2

4,1

родом'

при парциальном

давлении

его в га3овой

фазе, равном

атмосфр-

ному'

дол)кен

равняться

.---

#езош

:_2,Ф6в.

|[аршиальное

давление

атомарного

водорода в

равновесии

€ йФ]тё-

кулярным

водородом

при

атмосфрном

давлении,аследовательно'

и с

адсор-

бированньтм

водородом

при потенциале

нормального водороднФ|Ф

3.[ё(:

трода' таким образом,

равно

бшъз

:|0-3-",5

а|пм.

3то

давление

соответству1ощая

ему концентрация неизмеримо

мальт'

мех<ду

тем. как

концентрация

адсорбированного

водорода' например'

в случае

платинового электрода'

при потенциале

нормального водород-

ного

электрода'

как следует

и3

кривь1х заря)кения'

весьма 3начительна.

8 главе ||| мь]

вернемся к вопросу о

зависимости энергии

адсор6

ции

от природь1 металла.

9. АдсоРБция

кислоРодА

и окиснь|в

слои

Фсобенно глубокое

влияние

на электрохимические свойства

метал-

лов' как будет

показано в

главе!1|'

ока3ыватот

находящиеся на их

поверх'

ности атомы

кислорода.

/\4.

Фарадей объяснил

переход металлов в

пас-

сивное состояние

(в

котором

способность металлов

посылать собственньте

ионь!

раствор

сни}кается. или

полностью

исчезает)

появлением ъ1а |!х

поверхности кислорода.

Больхшое 3начение

для

обоснован'1я

кислородной

теории пассивности имели исследования акад.

в. А.

(истяковск616

[{01,

посвященнь1е окиснь|м

слоям.'

1(ак и в случае-адсорбции

водорода'

метод кривь1х зарях(ения мол{ет

быть с

успехом

применен к

исследованию

свойств адсорбированного

кис-

лорода и окиснь|х

слоев.

Аз

рис.

30 видно' что

при

анодной

поляризации

платинового

электрода после

прохо'{дения

участка

кривой 3арях(ения,

в котором

емкость электрода

сни>кается

до

3начений,

соответствующих емкости

двой-

ного

слоя' наклон

кривой 3аря)кения

вновь

умень1пается'

т. е. емкость

электрода

увеличивается.

3то

повьт!пение емкости свя3ано

с посадкой

на

поверхность атомов кислорода*,

во3ника}ощих

3а счет

разряда

моле_

кул воды

или

ионов

гидроксила

по

реакциям

Ё'Ф--+Ф^'"у2|7'

|2е,

2ФЁ-

Ф.^.

|1'Ф

2е.

Б слун:!е платинового электрода

растворах

Ё'5Фд и

Ё€] кислород-

11ая

и водородная части

кривой заря>кения

четко

отделень1

друг

от

друга

<двойнослойной> областью.

щелочньлх

растворах'

однако'

снятие водо-

рода

происходит

значительно

труднее'

так

что

при потенциалах' при кото-

рь|х

начинается

посадка кислорода'

еще не весь водород

удален

с поверх-

ности

(рис.

30); водородная

и кислородная области

потенциалов поэтому

непрерь|вно

переходят

одна

другу}о.

Рсли в

кислородной

части

кривой заря)кения направление

тока изме-

нить на обратное,

то мо)кно снять

полную

катоднуто

кривую заря)кения;

при этом электрод

проходит через

кислородную'

двойнослойную

и водо-

родну!о

о6ласти

в обратной

по сравненито

анодной

кривой 3аря)кения

последовательности.

||рямой

обратньтй

ход кривь1х

заря>кения

в этом

случае'

однако'

не'совпадают,

образуя

гистерезисную

петлю.

растворах'

содер)кащих

ионы

€1_

Бг-,

одновремевно

происходит

некоторое

растворение

платины.

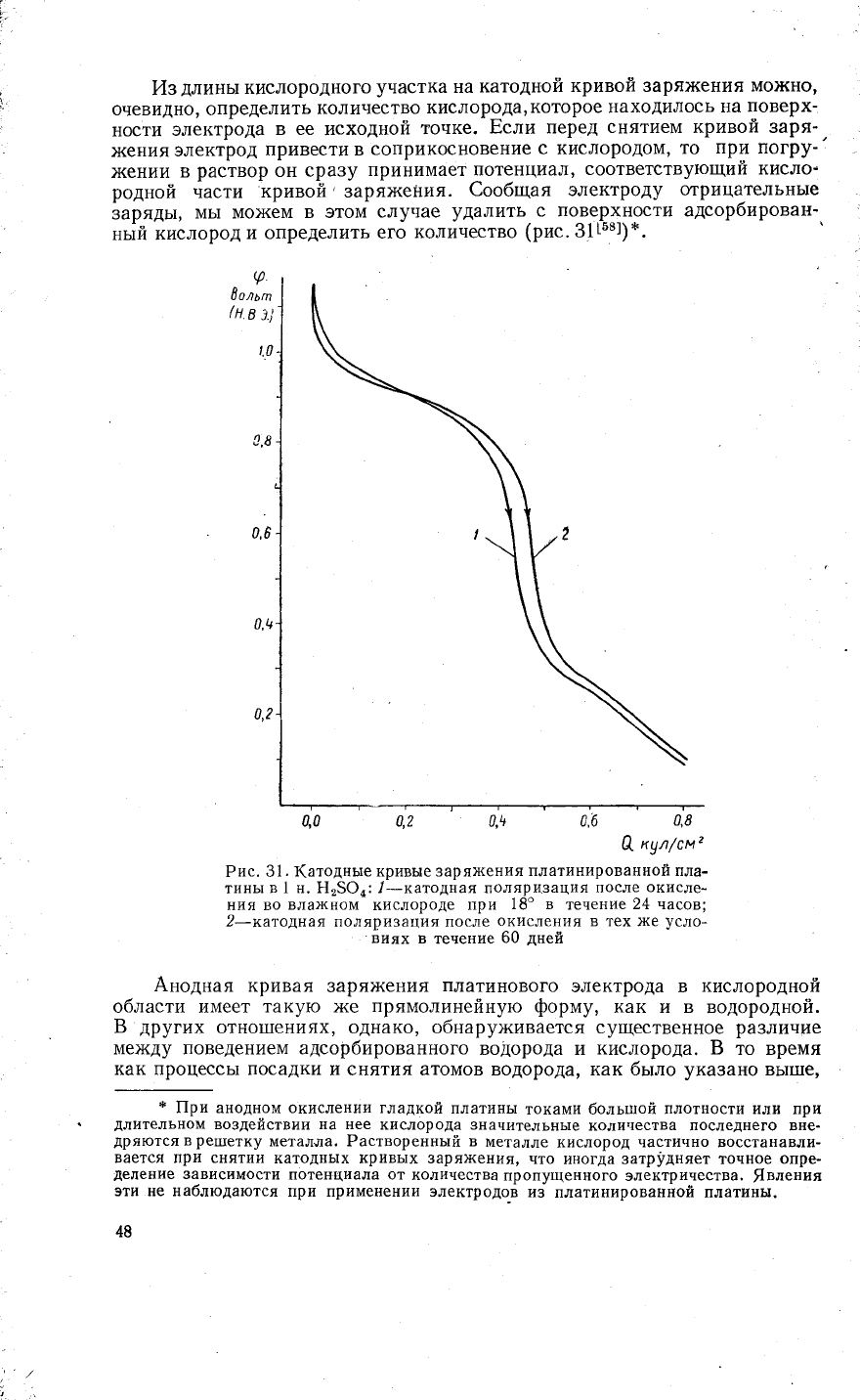
йз

длиньт

кислородного

участка

на

катодной

кривой 3арях(ения

мо}кно'

очевидно' определить

кол ичествю

кислорода'

которое на

ходилос

н3

11ФБе!1-

ности

электрода

в ее

исходной

точке.

Рсли перед

снятием кривой 3аРя',

х{ения

электрод

привести в

соприкосновение

кислородом'

то

при

погру_

)кении

раствор

он сразу

принимает

потенциал,

соответствующий

кисло'

родной

тасти

кривой' зарях<ения.

(66(тт1ая

электроду

0трицательнь1е

3арядь|,

мь] мо>кем

в этом

случае

удал|тть

-с

по_веР1.н9сти адсорбирован_,

,ь:й кислород

и определить

его

количество

(рис.31|58])*.

0ольп

/н'в

''}

1,0

кул/см'?

Рис. 31.

(атодньте

кривь!е зарях{ения

платинированной пла-

тинь|

в 1 н. Ё'5Ф,: !-катодная поляризация

после

окисле-

ния во

вла)кном

кислороде при

18' в

течение

24 насов;

кат

дн

а я'",

]3##ч

}&ъж

ъЁ

;{:},

в тех )ке

усло_

Анодная

кривая

3арях{ения

платинового

электрода в

кислородной

о6ласти имеет

такую >ке

прямолинейну]о

форму,

как и в

водородной.

других

отно1шениях' однако' обнару>кивается существенное

различие

мех{ду поведением адсорбированного

водорода и

кислорода. Б

то время

как процессь1 посадки

т4 снятия атомов водорода' как бьтло

ука3ано

вь|тпе'

|!ри анодном окислении гладкой

платинь]

токами больтпой

плотности или

при

длительном

воздействии на нее

кислорода значительнь|е

количества последнего вне-

дряются

ре1|1етку

металла. Раствореннь:й в

металле

кислород

частично восстанавли-

вается при снятии

катоднь|х кривь!х заря}кения'

что иногда затр1[лняет точное

опре-

деление

зависимости

потеЁциала

от

количества

пропущенного

электричества.

[вления

эти не наблюдаются

при применении электродов

из

платинированной платины.

0.8

0,6

0'ц

0,24,0

обратимы

(по

крайней

мере

если

они

проводятся

не сли1шком

быстро),

анадогичнь1е

процессь|

в случае

посадки

и снятия

кислорода

явно

необра-

тимы'

состояния'

чере3

которь]е

проходит

электрод

в кислородной

части

кривой

3арях(ения'

нельзя

расематривать'

как

равновесныё.

Ёеобрати-

мость

эта ска3ь]вается'

в частности'

ра3личии

фрмь:

анодной

и катод_

ной кривьтх

зарях<ения

кислородной

области'

Ёа катодной

кривой,

как

видно

из

рис.31,

кислородной

части

имеется

характерная

3адерх{ка'

соответству}отт|.ая

снятию

больгпей

части

адсорбированного

кислорода'

то

время как

на

анодных

кривь|х посадка

кислорода

приводит

только

умень1пени1о

наклона-кривой

заря}кения,

без появления

такой

задержки

(кривьте

н25о4 и

}(ФЁ,

рис.

30).

€вязь

ме'(ду

металлом

кислородом

имеет

полярнь:й

характер'

и по_

явление

слоя адсорбированньтх

атомов

кислорода

вь]зь|вает

существен_

1,0

0олоп

(н

в.э

)

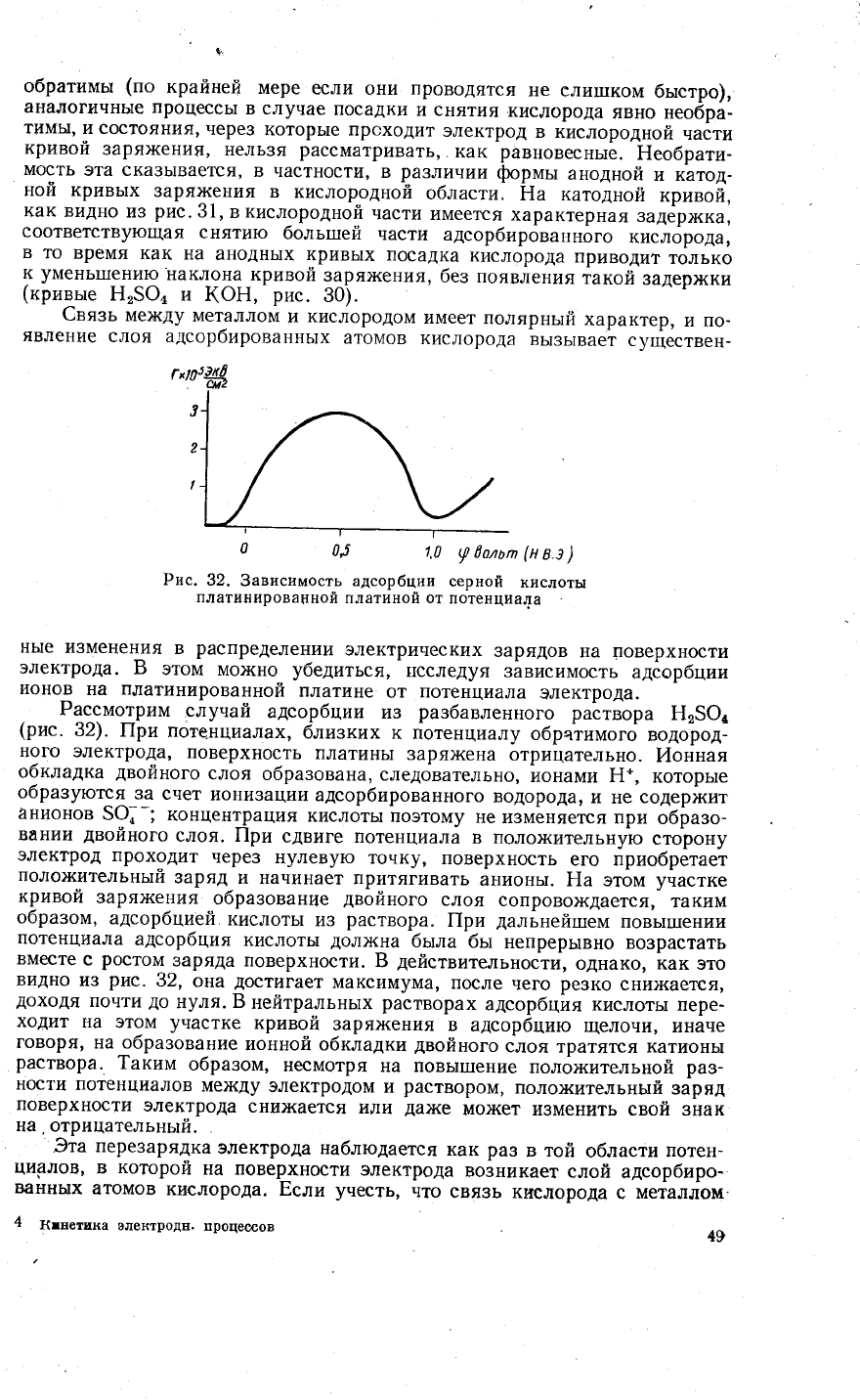
Рис.

32.

3ависимость адсорбции

серной

кислоты

платинированной

платиной от

потенциала

ные

и3мене1ия

распределении

электрических

зарядов

на

цоверхности

электрода.

этом

мо)кно

убедиться,

]]сследуя

3ависимость

адёорбции

ионов

на

платинированной

платине

от

потенциала

электрода.

Р19чмо]рим

случай

адсор6ции

и3

разбавленного

раствора

н25од

(рис.

32).

|!ри

потеншиалах'

6лизктах

к потенциалу

обра1имого

водород-

ного электрода'

поверхность

платинь1

зарях{ена

отрицательно.

1'1онная

о6кладка

двойного

слоя

образована'

следовательно'

ионам!!

Ё*, которь1е

образуюгся

3а счет

иони3ации

адсорбированного

водорода'

и не

содер>кит

анионов

5Ф.

концентация

кислоты

поэтому

не изменяется

при

об}азо_

вании

двойного

слоя.

|!ри

сдвиге потенциала

в поло)кительну}о

сторону

электрод

проходит

через

нулевую точку'

поверхность

его приобретает

полох{ительнь:й

заряд-и

начинает притягивать

анионы.

Ба этом

унастке

кривой

3арях(ения

образованце

двойного

слоя

сопровох(дается'

таким

образом,

адсорбцией.

кислоть!

из

раствора.

|1ри

дал!ней:пем

повь]1пении

потенциала

адсорбция

кислоть|

долх(на

бьтла

бьт

непрерывно

возрастать

вместе

ростом

3аряАа поверхности.

действительностй'

однако' как это

видно

и3

рис.

32, она

достигает

максимума,

после

чего

резко

сни}кается'

доходя

почти

до

нуля.

нейтральнь1х

растворах

адсорбцйя кислоты

пере-

ходит

на этом

участке

кривой

3аряжения

адсорбцию

щелочи'

иначе

говоря'

наобразование

ионной обкладки

двойного

слоя

тратятся

катионы

раствора.

1аким

образом,

несмотря

на повь|1'цение

поло)кительной

раз-

ности потенциалов

ме}кду

электродом

раствором'

поло]{<ительный

3аряд

поверхности

электрода

сних(ается

|4л|4

да}{е

мох{ет

и3менить свой знак

на. отрицательнь:й.

3та

перезарядка

электрода наблюдается

как

раз

той

области

потен-

ци3лов'

которой

на

поверхности

электрода

возникает

слой

адсорбиро_

в{|нных

атомов

кислорода.

8сли

унестБ,

91Ф

свя3ь

кислорода

металдом-

к:ветцка

алектродп.

процеосов

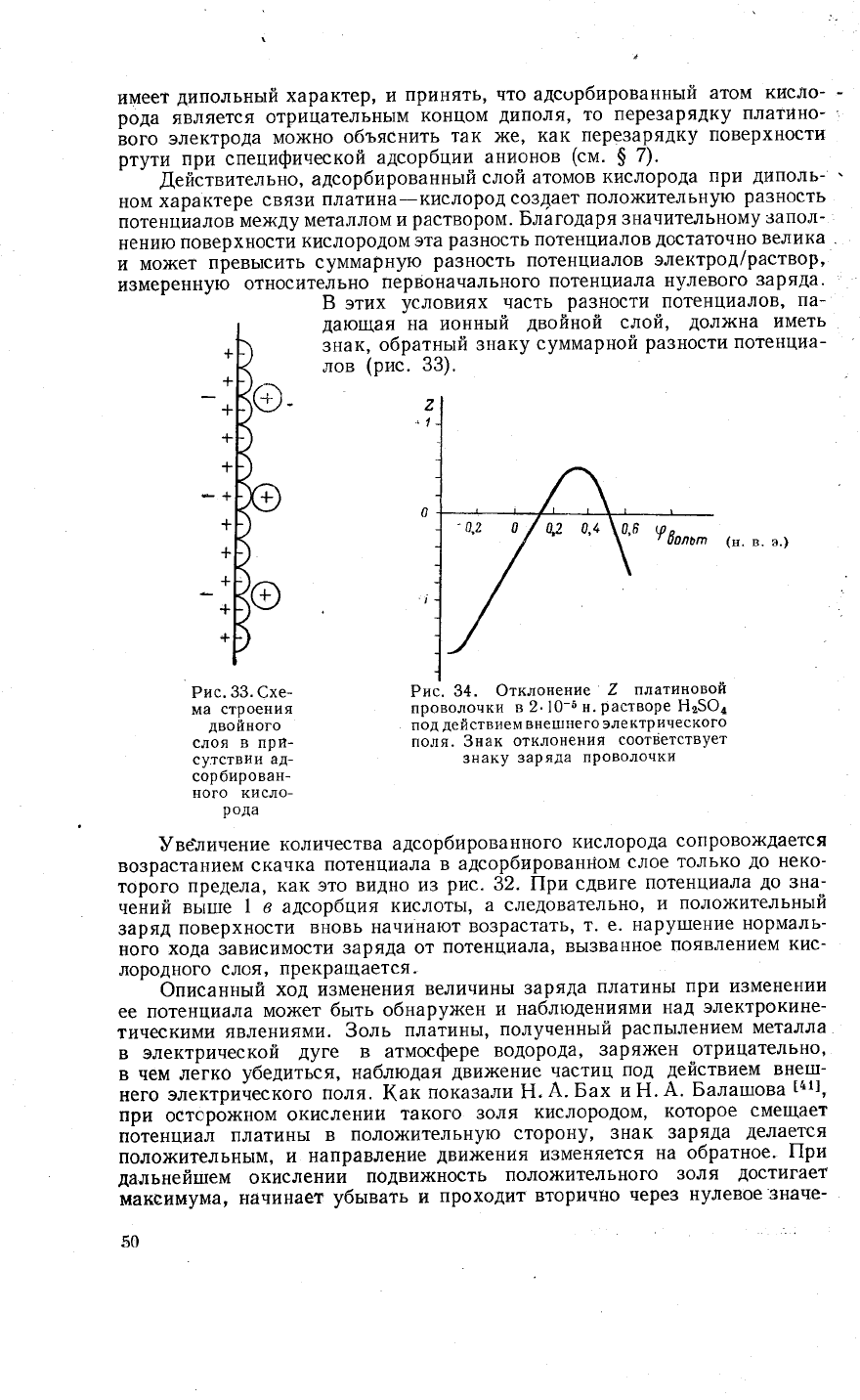
имеет

дипольнь1й

характер'

принять, что адс0рбированнь1й

атом кисло-

рода

является

отрицательнь1м

концом

диполя'

то

перезарядку

платино-

вого

электрода

мо)кно

объяснить

так )ке'

как.пере^зарядку

поверхност]4

ртути

при специфической

адсорбции

ани_онов

(см.

7).

.[1ействительно,

адсорбированнь1й

слой

атомов

кислорода

при

диполь-

ном

характере

связи

платина

кислород

создает

поло}кительную

разность

потенциалов

мех{ду металлом

раствором.

Благодаря

3начительному

запол-

нению

поверхности

кислородом

эта

разность

потенциалов

достаточно

велика

и мо)кет

превь]сить

суммарную

ра3ность

потенциалов

электрод/раствор,

измеренную

относительно

первоначального

потенциала

нулевого

заряда.

Б этих

условиях

часть

ра3ности

потенциалов,

па-

дающая

на ионнь|й

двойной

слой,

дол}кна

иметь

знак,

обратнь|й

знаку

суммарной

разности

потенциа-

лов

(рис. 33).

(п.

в. э.)

Рис.

33.

€хе-

ма

строения

двойного

слоя в при-

сутствии

ад-

сорбирован-

ного

кисло-

рода

Рис.

34.

Фтклонение

платиновой

проволочки

!0_5

н.

растворе

Ё25Ф'

под

действием

внешнего электрического

поля. 3нак

отклонения

соответствует

знаку

заряда

проволочки

}ве)личение

количества

адсорбированного

кислорода

сопровох{дается

во3растанием

скачка

потенциала

в адсорбированном

слое

только

до

неко-

торого

предела'

как это

видно и3

рис.

32. [|ри

сдвиге

потенциала

до

3на-

чений

вьгш-те

в адсорбция

кисло;ь1,

а следовательно,

поло}кительнь|й

заряд

поверхности

вновь начинают

во3растать,

€. нару1пение

нормаль-

ного

хода

зависимости

заряда от

потенциала'

вь13ванное

появлением

кис_

лородного

слоя'

прекращается.

Фписанньтй

ход изменения

величинь|

3аряда

платинь|

при изменении

ее потенциала

мох<ет

бьтть обнару)кен

и наблюдениями

над

электрокине-

тическими

явлениями.

3оль

платинь1'

полученнь]й

распь:лением

металла

в электрической

дуге

в атмосфере

водорода'

заря'(ен

отрицательно'

чем легко

убедит|ся,

наблюдая

дви)кение

частиц

под

действием

вне1п-

него

электрического

поля.

ка'

показали Ё.

А. Бах и

н.

А.

Бала:пова

[&1],

при

остсро)кном

окислении

такого

3оля

кислородом'

которое

смещает

потенциал

платинь1

полох{ительну!о

сторону,

знак

заряда

делается

полох<ительт{ь|м'

и направление

дви)кения

и3меняется

на обратное.

|1ри

дальнейшем

окислении

подвих{ность

поло)кительного

золя

достигает

максимума'

начинает

убь]вать

проходит

вторично

через

нулевое'значе-