Фрумкин А.Н., Багоцкий В.С., Иофа З.А., Кабанов Б.Н. Кинетика электродных процессов
Подождите немного. Документ загружается.


3ная
толщину
дифу3ионного
слоя'
мох{но
вь1числить
плотность
тока
к
поверхности
электрода
по
основнь1м
фр-мулам
диффузионной
кинетики:
.
пРР
(со-ё)
-ь,
.
пР|со
.а-._.
о
Б
рассматриваемой
теории
формула
(82),
однако'
по своему
смь1слу
существенно
отличается
от соответствующей
формульт
в
теории
Ёернста
(77),
так ка^к
толщина
Б,
фигурирующая
в
знаменателе
Ёравой
!'|'й
уравнения
(32),
не
есть толщина
неподви)кного
слоя;
напротив'
в
этом
слое]1роисходит
постепенное
нарастание
скорости
двих{ения
х<идкости
*.
Бторое
вах{ное
отличие
по сравненито
с
тёорией Ёернста
3акл}очается
в том'
что
величина
8
зависит
не только
от скорости
двих{ения
(переме_
гшивания)
}кидкости'
но так}ке
и от коффициента
диффузии
разрях{а}о_
щегося
вещества.
Фтсюда
следует'
что при
одинаковь]{
геометрических
и
гидродинамических
условиях
величина
Б
не
являетея
постоянной,
а зависит
от природь1
реагирующих
на
поверхности
электрода
частиц.
3ещество,
обладающее
больгшим
коэффициентом
диффузии,
успевает
Аиф-
фундировать
к поверхности
электрода
из больтпей глу6иньт,
т. е. толщина
лиффузионного
слоя
для
него
больтпе, чем
для
вещества
с меньйим
коэф-
фициентом
диффузии.
Фтсюда
вь]текает
интересное следствие
о
том'
что плотность
диффузионного
тока пропорциональна
коэффишиенту
лиф-
фузии
не в
первой степени,
как это имело
место
в
рассмотреннь]х
ранее
случаях
4ифФузии
в
покоющейся
>кидт<ости
и
как
это
принимал
Ёёрнст
и
Аля лиф^фузии
в
дви}кущейся
>кидкости,
а
коэфицйенту
диффузии
в степени
2/*:
!'
ъ
2||2|з
ц[|2
у-з'1в
*-л/э
16о
_
с.).
(в3)
|[равда,
различие
в
зависимости
тока
диффузии
от
коэфит]иента
диф_
фузии
(по
теории
Ёернста
-!
-
о,
по
теории
,[{ёБича !
*
|2|э\
йе имеет
очень
больщого
практического
3начения,
так
как
коффициенть1
дифузии
раз_
личнь1х
веществ колеблются
в
довольно
узких
пределах.
Ёо
все'{е
разли_
чие это принципиально
ва)кно'
поскольку
оно показь1вает'
что мь1
имеем
дело
с
двущя
различнь]ми
карт\4нами процесса
диффузии.
Б
то время как
в теории
Ёернста
предполагалось,
что величина
8
задается
распределе-
нием
скоростей
в х{идкости'
в современной
теории эта величина опреде-
ляется
у'{е
протеканием
самого пРоцесса
дифузии.
3то
разлиние
вь1сту-
пает
еще
ярче
при
рассмотрении
более сложнь]х случаев конвективной
диффузии,
на чем
мьт
здесь'
однако'
не
мо)кем
останавливаться.
Ёаиболее
вах{ное
отличие мех<ду
о6еими теориями
3аключается
в
том' что величина
8
в теории.[1евича
не вводится
в
качестве произволь-
ной
постоянной,
как
это
имело место
в теории
}1ернста,
а
приобретает
определенньтй
физинеский
смь;сл.
$
9. вРА!цАющийся
дисковь!й
элвктРод
А4ьл подробнее
разобрали
слунай электрода
в виде тонкой
пластинки,
находящейся
в
струе
раствора'
в
первую
очередь потому'
что на
нем
нагляд-
+
Б
связи
с этим мо)кет во3никнуть
вопрос о
законности
применения
уравнения
(82),
вьтведенного
для
случая покоящегося
пристеночного
слоя. Фднако,
как
показь1-
вает
расчет' распределение
концентрации
в
дви)кущейся
>кидкости
вблизи поверхности
эле(трода
является почти
линейнь1м' что позволяет
с
достаточной
ётепенью
точности
поль3оваться
уравнением
(82).
(82)
(32а)
в|
6
кинетина
эле|{тродн. процесоов

но мох(но
проследить
характер
двих(ения
х(идкости. Рассмотрим
в
даль-
нейтпем
слунай электрода
в виде
врап(ающегося
диска.
3лектрод
такой
фррмь:
часто применяется при
электролизе.
|1ри
бьтстром
вращении
дискового
электрода
вокруг' оси, проведенной
через
его
центр
перпендикулярно
к
плоскости
А||ска,
х(идкость'
сопри-
каса1ощаяся
с
центральнь1ми
частями
диска'
отбрасьтвается
центробех<ной
силой
к
его
краям.
Бследствие
этого
около
центра
дискасоздается
разре-
'{ение'
и
струя ,(идкости направляется
из объема
раствора
к
центру
диска.
[|инпи
двих(ения
)кидкости
имеют
вид, изобрах<енньтй
на
рис.
50.
8сли
учесть'
что
струя
раствора
из объема
набегает
на
центр
диска,
то
по
мере
продвих(ен||я
к краям
диска
толщина
граничного
слоя
дол)кна
бь:ла бь:
во3растать. €
другой
стороньт'
по
мере
продви'{ения
к краям
во3растает
ли-
.
нейная скорость
двих<еЁия
точки
на
диске'
вследствие
чего
толщина эта
долх{на
уме1{ь!питься.
.[!егко
видеть из
соотно1пения
(79)'
что эти
два
влияния
в3аимно компенсируются.,(ействитель-
но' возрастание толщиньг 8",
происхо-
дит
пропорционально
корню
и3
рас-
стояния
от точки
набегания, т.
е.
в
данном
случае корню
и3
радиуса.
{,|инейная скорость
движения
точки на
диске
пропорциональна
радиусу'
а
тол-
щина
8гр
обратно пропс|ршиональна
корню
из
линейной
скорости. Б
итоге
получается'
что толщина
граничного
слоя
|-{рандтля
одинакова
для
всех
точек
на
поверхности
вращающегося
диска.
||о
этой
причине
гидРодина_
мическая
задача
упрощается,
|4
для
этого случая
дифузионну1о
3адачу
мо)кно
ре1шить
до
конца.
||ервь:й
в-ь|вод' которьлй
мо)кно сделать'
заключается
в том, нто
диффу-
зионный слой, так >ке
как
и
граничньтй
слой,
имеет
одинаковую тол-
щину
для
всех
точек поверхности вра'тт3ющегося
диска.
Бследствиеэтого
и
плотность
тока во
всех'точках
одинакова'
Ёсли
осах<дать
на вращаю-
щемся
дисковом
электроде
какой-либо
металл'
например'
медь' то он
покрь|вает
вс1о поверх}тостьдиска
ровнь|м
слоем' толщина которого
у
краев
и
у
центра
одицакова.
Расчет
дает
для
толщиньт
диффузионного
слоя
на вращатощемся
дисковом
электроде:
с
}
:
|,62
о1|3\1!в
о-1|2,
(в4)
где Ф
_
угловая
скорость
вращения
(т.
е. тисло оборотов
в секунду'
умно-
}кенное
на 2
п).
|1ользуясь этим
вь[ра)кением'
находим
для
плотности
тока
!:0,62пРо2|3
Ф1/2
у_1/6
(с0_
6.;.
(в5)
1(ак
упоминалось'
на
опь]те было
ух<е
дав!{о
найдено
[7!,
нто
дифузион-
ный
ток врап]ающегося
дискового
электрода
пропорционален
примерно
Ф0'6.'
Ёебольтпое
отклонение
мех{ду
пока3ателем
0,6,
вь1текающим
из
этих опы-
тов'
и показателем 0,5,
требуемымтеорией, происходит
оттого' что при по_
становке
опь1тов не были соблюдены
условия'
по3воля1ощие
избех<ать обра-
3ования
вихрей.
8сли
принимать такие
меры
предосторо)1(ности'
то
82
Рис. 50.
.['вих<ение
'(идкости
вблизи
вращающегося
дискового
электрода
т-
+---т=
_-х/}*:
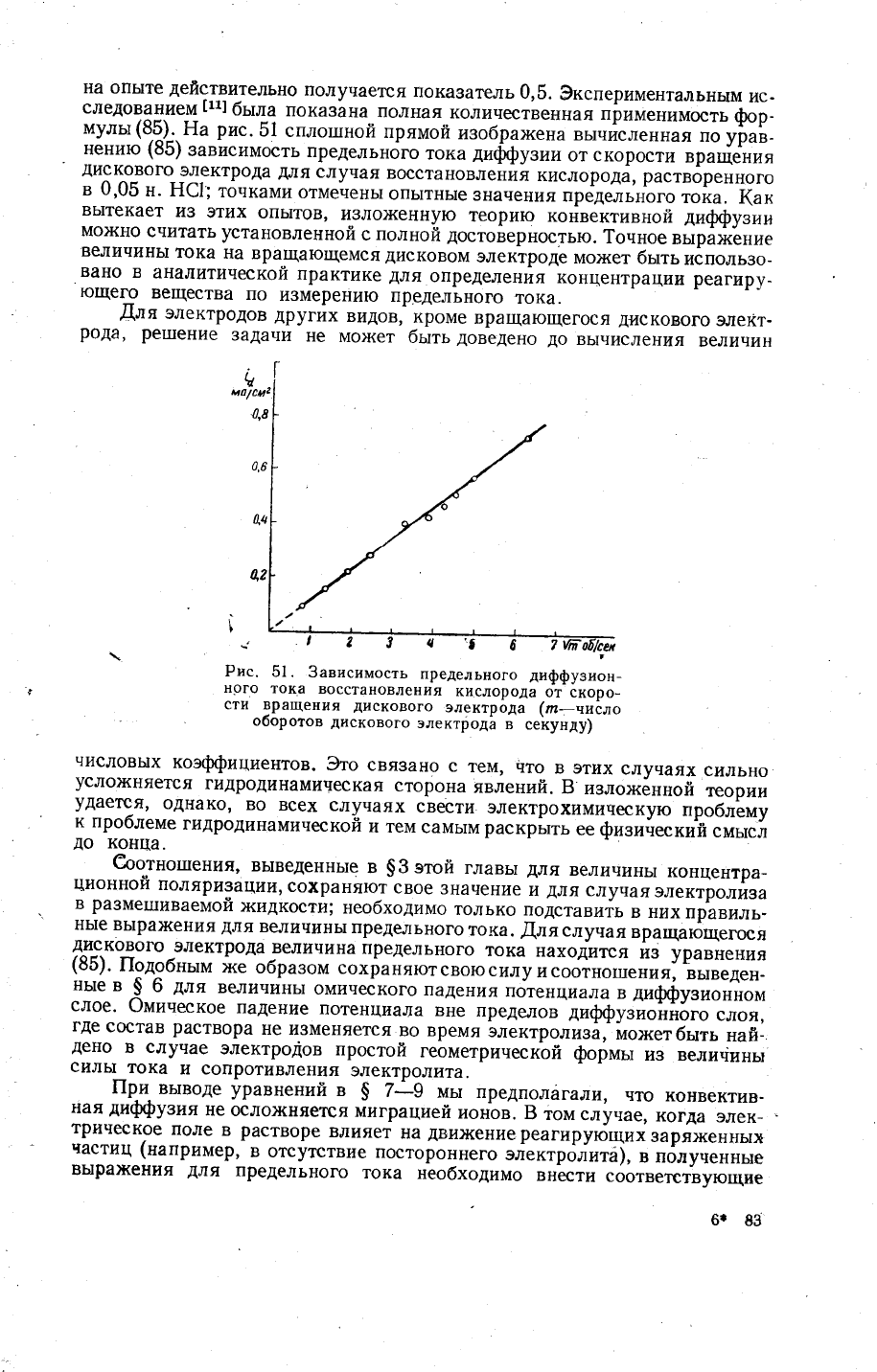
на
опыте
действительно
получается
показатель
0,5.
3кспериментальным
ис_
следованием
[11]
бьтла
пока3ана
полная
количественная
применимость
фр-
муль:(8.5}.Ёа
рис.
51
сплошлной
прямой
изобра>кей'
",''Ё"'""ная
по
урав_
нению
(85)
зависимость
предельного
тока
д'фузйй
й.йБр'".,
вращения
{"х 1'3_'.ч'тектрода
дпя
случая
восста
новления
кислорода,
растворенного
в
(-,,05
н. пс];
точками
отмечень|
опь|тнь1е
значения
предельного
то|а'
1(ак
вь|текает
и3
этих опь]тов'
и3ло)*(енную
теорию конвективной
диффузии
мо}кно
считать
установленной
с
полной
достоверностью.
1очное
вырах(ение
величины
тока
на
вра.щающемся
дисковом
электроде
мох(ет
быть
иёпользо-
вано
в
аналитической
практике
для
определенйя
концентрации
реагиру_
ющего
вещества
по
измерению
предельного
тока.
,{,ля
электродов
других
видов,
кроме
вращающегося
дискового
ат|ект-
рода'
ре1шение
3адачи
не
мо}кет
быть
доведено
до
вь!числения
величин
[,г
мо/сп2
!,8
Рис.
51.
3ависимость
предельного
диффузион_
::;"
9;ж',т"}1'ъ?.1"#:
",
}Ё*{,!#'
с}'#3,%
.
оборотов
дискового
элект!од!
в
се!<унду)
числовых
коэфит{иентов.
3то
связано
с
тем'
что
в этих
случаях.сильно
услох(няется
гидродинамическая
сторона
явлений.
3
изло>кЁн,'й
й'рйй
удается'
однако,
во
всех
случаях
свести
электрохимическую
проблёму
к проблеме
гидродинамической
и тем
самь1м
раскр'ть
ее
физинеский
смьтсл
до
конца.
0,оотношления'
выведеннь|е
в
$3
этой
главь1
для
величинь|
концентра-
ционной поляризации'
сохраняют
свое
значение
||
для
случаяэлектролиза
в
разме]'|]иваемой
>кидкости;
необходимо
только
подставить
в них
правиль.
нь|е
вь|ра)ке|1ия
д]\я
величины
предельного
тока.
!дя
слуная
вРап\ающегося
А1т"*: ::.т-"_11р'д.
вели
ч
и на й
редел
ь
но го
то
ка на
ходитс
й
_й
;
;;ы;
;;
;
(65).
|
|одобнь|м
>ке
образом
сохраня}отсво}осилу
и
соотно1пения'
выведен_
ные
в
$
6
для
величинь|
омического
ладен\4я
потенциала
в
дифузйБйом
слое.
Фмическое
падение
потенциала
вне
пределов
дифузионного слоя,
где
состав
раствора
не
и3меняется
во время
электролиза,
йох<етбыть
най].
дено
в случае
электро,:|ов
простой
геометринескоя
6ормь:
из вели.|ины
силь1
тока
и сопротивления
электролита.
||р.и
вь:воде
уравнений
в
$
7-_9
мы предполагали'
что
конвектив-
ная
ди(рФузия
не
ослох{няется
миграцией
ионов.
3
том
случае'
когда
элек-
:Р::::-::_ ]9{е
в
растворе
влияет
на
двих<ение
реагирут6щих
за
ря)*(еннь]х
частиц
(например'
в
отсутствие
постороннего
электр6лита),
в полувенные
вырахения
для
предельног0
тока
необходимо
внести
соответствующие
6.
в3

поправки'
как это бьтло
изло>кено
в$5.
Фднако'
вслучае
размегпиваемой
>кидкости
количественнь]й
учет
миграции
ионов
несколько
отличается
от
случая
покоящейся
)кидкости.
1ак,
при
разряде
одновалентнь1х
катио-
нов
в
разме1шиваемой
}{{идкости
миграция
вь]зь1вает
увеличение
предель_
ного
тока
не в
два
раза
(см.
уравнение
7|),
а в мень1шем
отно1пении.
$
10. уРАвнвнив
нвстАционАРной
диФФу3ии
для
плоского
элвктРодА
Б предьтдущих
разде.'1ах
мь]
рассмотрели
те
явления'
которь1е
проис-
ходят
при
стациона}ной
диффу3ии,
т.
е.
при таких
дифу3ионных
процес-
сах,
скорость
которь]х
ух{е
установилась
и в
дальней1пем
во времени
не
мЁняетсЁ.
|1редставляет
интерес
так)ке
рассмотрение
диффузионнь1х
процессов,характеркоторь|хещенеустановилсяискоростькоторь1х
во
времени
еще
меняется.
и3учение
этих
явлений
имеет
3начениепо
двум
причинам.
Бо-первьтх,
в некоторь1х
случаях
мь1 вс'тречаемся
на
практике
именно
с такими
нестационарнь1ми
процессами.
Фдин,
весьма
ва)кнь!й
"'.у"!й-д"фузия
на
капельном
ртутном
электроде-булет
в
дальней_
й"''
1"дЁЁо1то'разобран.
Бо-вторьтх,
при
рассмотрении
стационарнь;х
диф-
фузионных
процессов
делается
допущение
о
том'
что
стационарное
состо_
"й'"
'о'^ет
бь|ть
достигнуто;
это
допущение
требует
доказательства'
которое
мь1
опустили
в
предь1дущих
рассух{дёниях.
||оэтому
без
рассмо_
тренйя
нестационарнь!х
состоят1ий,
воо6ще
говоря'
нель3я
получить
пол-
ную
уверенность
в
правильности
трактовки
стационарн,1!
-|р91!!!9^";
-
9тметим,
что
первое
правильное
ре1ление
задачи'
нестационарнои
дифу3ии
при\(енительно
к электрохймической
проблеме
бьтло
дано
А"п.
€околовьтм
(1в90)
{121.
Ёачнем
рассмотрение
неста|1ионарной
диффу3ии..
с
самого
простого
случая
плоского
электрода,
погрух<енного
в
больтшой
объем
раствора'
которьтй
не
переме1пивается'
например,
серебряного
электрода
в
растворе
азотпокислого
серебра
в
присутствии
у|з6ь|тка
индифферентного
электро-
лита'
3тот
раствор
имеет
во всех
точках одинаковь1й
состав,
т. е.
одинако_
вую
концентрацию
ра3ря)кающихся
ионов.
3
некоторь]й
момент
времени,
которьтй
мь]
обозначим
!:0,
на
электрод
накладь|вается
значительная
катодная
поляри3ация
(пр].1
помощи
лю6ого
вспомогательного
электрода'
погрух{енного
в
раствор).
всли поляри3ация
серебряного
электрода
доста_
точно велика'
концентрация
ионов
серебра
у
его
поверхности
сразу
упаде_т
практическ'\
до
|1уля
вследствие
процесёа
катодного
ра3ряда
ионов
сереб-
р!.
Фдновременно
начинается
процесс
диффузии-ионов
серебра
и3
объема
раствора
к
поверхности
электрода.3адача
сводится
к
нахох{дению
распре-
деления
контт.ентрац\4и
ионов
в
растворе
в
любой
момент
времени'
3ная
это
распределение
концентрации'
мо)кно
легко
вь1числить
величину
диф_
(т1'зионного
тока.
3та
диф}зионная
задача
имеет
аналоги:,1
в
целом
рядедругих
явле-
х+ий
физдкй,'1
,,"'"ости,
в
явлениях
теплопроводности.
9вление
диф-
фузий
в
рассматриваемом
нами
случае
полностью
соответствует
явленик)
теплопроводности
в
бесконечно
боль1шом
теле'
в'котором
первоначально
температура
во всех
точках
бьтла
одинакова
и
которое
3атем
начинаетохла-
}кдаться
ввиду
того'
что
плоская
граница
тела
приобретает
более
низ-
,
ку1о
температуру.
Ё'",р"д"'е,'"
тёмпературьт
в
этом
теле в
лю6ой
момент
времени
и
тепловой
поток
в
нем
совер1пенно
аналогичнь]
распре-
делению
концентрац|\и
|4
д|4фу3ионному
току
в
растворе
в6л|1зц
плоского
электрода,
84

|1онятно,
что
рассматриваемая
дифузионная
задача
приводит
к нестационарному
процессу
диффузии.
||ервонанально во
всех
точках
имФ1ась одинаковая
концентрация
ионов; после
включения
тока
это
равномерное
распределение
нару1шается.
Ёарупление концентрации
сна_
чала
ограничивается
областьто
раствора
в6лизи
электрода'
а
3атем
распро-
страняется
на все больтшие
расстояния
от
поверхности
в
глубь
раствора.
Б
разньте
моменть1
времени
после начала нару1пение
распределения
кон_
центрации
булет
ра3лично.
9тобьт
дать
количественное
ре1пение
этой задани, необходимо
ре1т!ить
лиффузионное
уравнение'
которое
соответствует поставленнь]м
условиям.
Рсли
обозначить
расстояние
от
поверхности
электрода
по нап_равлени-ю'
перпендикулярному
поверхности'
через
х'
то' как мь1 видели в
$
2,
диффе-
ренциальное
уравнение
диффузии
имеет
вид
(в6)
где |_время'
про1пед1пее с начального момента
процесса,
А €:€(х,
|)-
концентрация
ионов
серебра,
которая является
функцией
не
только
расстоя-
н|4я
х'
но'
в отличие от
случаев стационарной
дифу3ии'
такх{е
и
времени
7.
||ри
этом мь1
делаем
предполо}кение' что
распределение
концен1рашии
при
передви)кении вдоль
поверхности не меняется' т. е.
что
во
всех точках'
находящихся
на одинаковом
расстоянии
от
поверхности'
концентрация
в любой момент
времени
одинакова. 1акое
предполох{ение мь|
вправе
сделать
в том
случае' если мь|
ограничимся
рассмотрением
той области
поверхности
электрода'
которая находится на
достаточном
расстоянии
от
краев электрода.
-|!1атематически
это
условие
вь]ра>кается требованием,
чтобы
расстояние
*
бьтло мало
по
сравнени}о с
ра3мерами
электрода;
часто это
условие форйулируется'
как
условие
бесконечного
размера
элек-
трода.
|1о
условиям
задачи
требуется найти
вь]рах(ение
для
концентрации
ионов
как
функшии
от
расстоян|1я
14
отвремени' которое
удовлетворяло
бь:
дифузионному
уравнению
(30).
(роме
того' искомое
ре1пение
дол}кно
удовлетворять
следующим краевым
условиям'
вь1текающим
и3
самой
суш-
ности
3адачи.
Б
момент времени
/:0
концентрация
во всех точках
имеет
одинаковое'
исходное
значение'
т. е.
0с'
-
'
02с
т-ц ах2
'
лри !:0 с:со.
Бторое
условие
гласит' что в любой момент после
включения
ризации
концентрация
ионов
у
самой поверхности
электрода
равна
т. е.
п!и#:0и[>0с:0.
(в7)
поля-
нул1о'
(88)
|1риведенное
диффренциальное
уравнение
с
краевь|ми
условиями
(87)
и
(88)
хоро[шо известно
и3 математической
физики{д3].
Реш:ение
этого
уравнения
имеет
вид
с(х,!):
е_!2ау.
(вэ)
этгй
Б
полуненное
ре1пение
входит определенньтй интегра,
\
е-у"7у.
о
|1еременная
у
в
|поду\нтегральном
вьтра'{ении
является вспомогательной
85
*
2тго'
^02
(
"
\/"
)
математической
величиной.
|{оскольку
определенный
интеграл
3ависит
толБйо
от вели(1ин
ни}|(него и
верхнеЁо
пределов'
эта переменная
исче_
зает в окончательном
ре1|]ении.
9исловь1е
3начения этого
интеграла
для
ра3ных
значений
верхнего
предела приведень!
в
специальнь|х
табли-
цах.
Бсли
верхний предел
обращается в
бесконечность' то'
как
и3вестно'
интеграл
принимает
3начение
е-ц'ё!:
\/;
-т
5
0
(00)
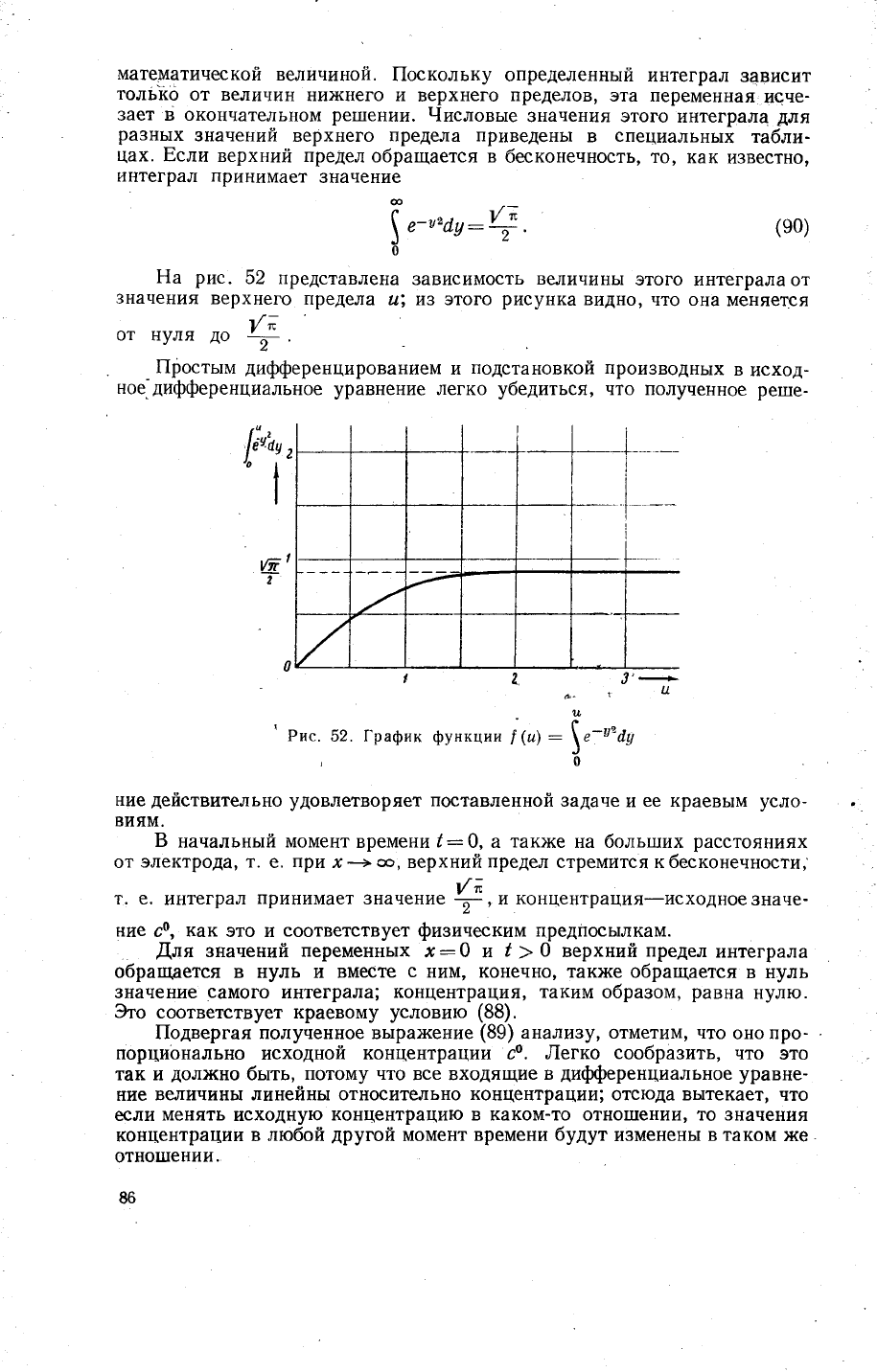
Ёа
рис.
52 представлена
3ависимость
ве.]|ичинь]
этого
интеграла от
значения
верхнего
предела
и;
и3 этого
рисунка
видно'
что она
меняется
\/;
от |1уля
до
-г
|1ростьтм
дифференшированием
и
подстановкой производнь|х
в
исход_
ное.дифференциальное
уравнение
легко
убедиться,
что полученное
ре1пе_
Рис.
52. [рафик
функции
[
(ц)
:
ние
действительно
удовлетворяет
поставленной
3адаче
и
ее краевь!м
усло_
виям.
Б
начальньтй
момент
времени
[:0,
а
так)ке
на больтцих
расстояниях
от
электрода, т.
е'
пр\4
х
ё ф,
верхний
предел
стремится к6есконечности'
\/;
т. е'
интеграл
принимает
значен^'
,
'
и
концентрация-исходное3наче-
ние
с0,
как
это и
соответствует
физинеским
предпосылкам.
Аля
значений переменнь|х
х:0 и
|
>
0
верхний
предел
интеграла
обраттиется в нуль и вместе
с
ним' конечно' такх(е
обрап(ается
в нуль
3начение
самого
интеграла;
концентрацу1я,
таким образом,
равна
нулю.
}то
соответствует краевому
условию
(88).
|[одвергая полученное вь|рах(ение
(89)
знадизу'
отметим' что
оно
про-
порционально
исходной
концентрации со' .[[егко
сообразить'
что
это
так и
долх(но
бь1ть,
потому что
все входящие
в
диференциальное
уравне-
т|ие
ве.,1ичины линейны относительно
концентрации;
отсюда вытекает'
что
если
менять
исходную
концентрацию в каком-то отно|шении' то 3начения
концентрации
в любой
другой
момент
времени будут
и3менень1
в таком
х{е
отно[цении.
86
\,-*',
0
|{олунен
ное
ре1пение
имеет
ха
ра
ктер ную особенность'
3а
ключающуюся
в том'
что интересующие
нас
переменнь1е-расстояние
,
и
время |-вхо-
дят
в
него не не3ависимо
друг
от
друга'
а
только
)(
в виде отно!пения
-
--..---"""
ут'
т.
е.
при
одинаковом
значении
этого отн01пения
концентрация имеет
одинаковое
значение'
не3ависимо от 3начений
х
и
[
в отдельности. 1аким
образом,
для
двух
точек
раствора,
находящихся
на
расстоянии
х1|1х2от
поверхности
электрода'
концентрация булет
одинакова
для
любьтх
двух
проме)кутков
времени
Ё,
(в
тонке
х')
и
|"
(в
тонке х'),
удовлетворяющих
условию
*1| )ф:{а|{Б.Фронт
диффузии
продвигается' таким обра-
3ом' внутри
раствора
на
расстояние'
которое
пропорционально
не вре-
мени'
а
корню
квадратному из времени.
3то происходит потому, что по
0'2
0,ц
0'6 0'8
!,['
/ мм
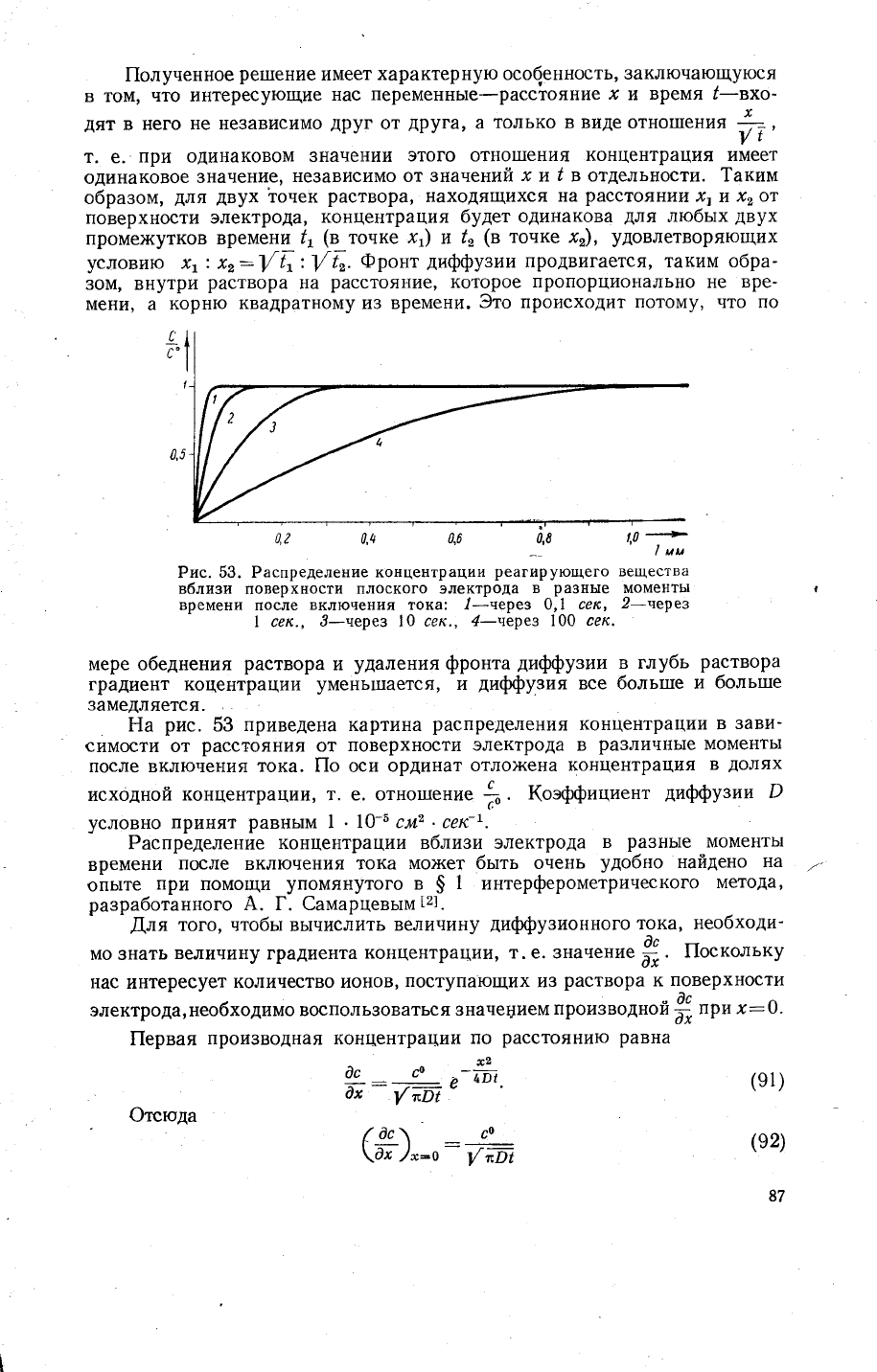
Рис. 53. Распределение
концентра.",
р",'"рующего
вещества
вблизи
поверхности
плоского 9лектрода
в
ра3ные
моменть!
времени после
включения тока:
.[-_через
0,1
сек,
2-нерез
! сек.,
3_нерез |0 сек.,
4-нерез 100
сек,
мере обеднения
раствора
и
удаления фронта
диффузии
в глубь
раствора
градиент коцентрации
умень1пается,
и
дифузия
все больтпе
и
больтпе
замедляется'
Ёа
рис.
53
приведена картина
распределения
концентрации
в
зави-
симости от
расстояния
от
поверхности
электрода в
различные
моменть]
после включения тока. |!о оси
ординат
отло)кена
концентрац!1я
в
долях
исходной
концентрациу!' т. е. от1{о1шение
:.
.
|(оффишиент
диффузип
Р
условно
принят
равнь1м
1
.
10_5 см2
.сек-|.
Распределение
концентрации
вблизи
электрода
в
ра3нь1е
моменть!
времени
после
включения
тока мох(ет бьтть
оче!{ь
}Аобно
найдено
на
опь1те
при
помощи
упомянутого
в
$
1
интерферометрического
метода,
разра6отанного
А. [. €амарше361у
[2).
'
Аля
того' чтобь| вь1числить
величину
дифузионного
тока, необходи_
мо знать
величину
градиента
концентрации, т.". ,",,""""
$.
||оскольку
!{ас
интересует
количество ионов'
поступающих
из
раствора
к
поверхности
электрода' необходимо
воспол
ьзоватьс я
3
наче}1ием
п
рои3водной
$
пртт
х
:
о.
|1ервая
производная концентрации
по
расстоянию равна
*2
0с
-
ф
._7-
ох
-
у;61
(д)
:-!:
\ох
/х-0
1/
в9[
(э1)
(02)
87
0тсюда

,
пР
|/бсо
.а
-
|т[
!:щд-(с,_с.),
у
т.с
(03)
(ак
видно
и3
уравнения
(93),
величина тока
дифузии
убьлвает
обратно
пропорционально
корн1о
квадратному
и3 времени. Рсли
продол}кать
про-
цесс
электроли3а
длительное
время' то сила тока
дойдет до
сколь
угодно
маль]х
знанений; отсюда вь]текает' что
в
рассматриваемом
случае
стацио-
нарное
состояние
концентрационной
поляризации
не
устанавливается.
Б первонанальный
момент времени
лри
!:0
плотность
тока'
согласно
уравненито
(93),
достигает
бесконечно больтпого
значения. 1акой
ре_
3ультат' естественно'
не имеет
физинеского
смь]сла. Фн
получи''1ся
и3-3а
упрощения'
которое мьт
ввели' когда считали' что
в момент
вклю-
чения тока концентрация
ионов
у
самой
поверхности
электрода
мгно-
венно падает
от исходного
значения
со
до
нуля.
|!ри таком
упрощении
в момент
времени |:0
получается
конечная
ра3ность
концентраций
на бесконечно
малом
расстоянии,
1.
€.
бесконечно больтпой
градиент.
Ёа самом
деле,
однако' концентрация-
у
поверхности электрода
падает
до
нуля не мгновенно'
а в течение некоторого'
правда' незначительного
проме}{утка
времени'
так что
обеднение
успевает распространиться
на не-
которое
расстояние
в
глубь
раствора.
3ависимость' вь1ра)кен}{ая
уравнением
(93),
бьтла опь1тно
проверена
в
ряде работ.
в.
м.
€кобец
и
Ё.
€. !(авецкий
[14]
измеРили и3менение
плотности
тока
диффузии
на твердом
электроде во времени.
Бо
всех
случаях
они на6людали
резкий
бросок
тока
при
3амь1кании
цепи'
а 3атем
сравнительно
медленное
падение
тока' подчиняющееся
закону
|{ри
вьтводе
полученнь|х
вь11пе
уравнений
предполагалось'
что
концен-
трация
ионов
у
самой поверхностиэлектродаравнанул}о'
т. е. чтодостиг-
нуто
преде]]ьное
3начение
тока
дифузии.
9тобьт
распространить
получен-
нь|е
ре|шения
у\ на тот
слунай'
когда концентрация
ионов
у
поверхности
не
равна
нул}о'
а имеет
некоторое постоянноезначение
(отлинное
от исход_
ного
3начения
концентрации),
достаточно
3аменить
повсюду
в этих
ре1||е_
ниях
исходну}о концентрацию
с0 на
разность
мех{ду
исходной
и
концент-
рацией
вблизи поверхности
со
_
св. Формула
для
тока
дифузии,
например,
перепи1шется
в виде
|
т/с'-
(э4)
т.
е. величинь|
для
тока
изменяются
по
сравнению
с
предельнь1ми
вели_
со
-фчинами
в
д
Раз.
$
11.
уРАвнвнив нвстАционАРной
диФФу3ии
!(*сФвРичвскому
элвктРоду
€лунай,
которьтй
будет
рассмотрен
в настоящем параграфе'
очень
6лизок к предыдущему
и отличается
от
неготолькогеометрическими
усло-
виями'
а именно: вместо
дифузии
к плоскому
электроду
будет
рас_
сматриваться
дифузия
к
электроду
сферической
формьт,
погрух(енному'
в бесконечно больгшой
объем
раств0ра.
88

Фбозначим
радиус
сферинеского
электрода чере3 г'.
Б
остальном
сохра-
ним
все
те
предполох<ения' которьте
бь:ли введень!
при
рассмотрении
пре-
дьтдущей
3адачи.
Б
момент
времени
|:'0 концентрация
ионов во всех точках
раствора
равна
исходной
концентрации; сра3у после
включения тока кон-
центрация
ионов
в6лизи
поверхности
начинает падать'
и
только
на боль-
1пом
расстоянии
сохраняется исходное 3начение.
|{ри изунении
процессов' происходящих
в6лизи
сферинеской поверх-
ности и 3ависящих
только от
расстояния
от
центра
сферь:,
а неот
вь:бора
направления
в
пространстве'
удобно
пользоваться сфринеской системой
координат. Фчевидно, нто в
сформулированной нами
задаче имеет место
такая сферинеская
симметрия и что
величинь|
концентрации
и
градиента
концентрации одинаковь1
для
всех
точек
раствора'
нахо_
дящихся
на одинаковом
расстояни|1
от
центра
сферине-
р
ского
электрода
(рис.
54).
|[о этой
причине
мо)кно
рассматривать
концентраци1о
в
любой
точке
раствора
и
в
любой момент
времени
как
функцию
двух
переменнь]х: времени | и
длиньт
радиуса-
вектора
г
(т.
е.
расстояния
от
центра
сферьт).
||ервое
граничное
условие
сохраняет
такой
х{е вид' как
и
для
предь]дущей задани, т. е.
лри
|:0 с:со. ($5)
Бторое
граничное
условие
принимает нескольцо от-
личньтй
3АА, так
как
поверхность
электрода
ух{е
не
характери3уется
декартовой
координатой
х:0,
как
это
бьтло
для
плоской
поверхности' а сферинеской коорди-
натой /: /6;
поэтому
при
г:
|о
А лри
[
}
0
с:0.
(96)
|1ри
переходе
к
сфрической
системе
координат
необ-
ходимо преобразовать
исходное
уравнение
дифузии,
которое принимает
вид
(3в)
Рис. 54' го-Ра_
диус
сферипе-
ского
электро-
да'
,.-расстоя-
ние
точки
в
ра-
створе
Р
от
центра
сфери-
ческого элект-
рода
'
02с1
+ар
]
(э7)
}равнение
(97)
мох<но получить
и3
уравнения
(86)
преобразованием
координат
из
декартовых
в сфринеские; мо>кно
такх(е непосредственно
вывести
уравнения
(97),
если
рассматривать
процесс
дифузии
к
сфри-
ческой поверхности'
аналогично
тому'
как мь1
это сделали при вь|воде
уравнения
(в6)
*.
Ретпение
диффреншиального
уравнения
(97)
при
граничнь1х
условиях,
приведеннь1х
вь11ше'
имеет
вид
{:о
г+*
*
.[,ействительно'
ра3ность
ме)кду потоками
диффузии'
входящим
в сфериве-
ский слой, ограниненвый
радиусами
г и
г
}
6г,
и
вь|ходящим
из него,
равна
}('".'!\4г,
а объ,ем
этого слоя
равен
4вг211г,
откуда
#:#|(+*ео#):,
11#+#].
89

.
}то
регшение
состоит
и3
двух
слагаемь1х'
и3 которь|х первоесовер1пенно
аналогично
ре1пению
предьтдущей
задани
(уравнение
39)
с той
лишь
раз_
ницей'
что в
верхнем
пределе
интегрирования
фигурирует
расстояние
не от
плоскост|1,
а от
поверхности
сферь:
и нто
коэфициег1т
перед
интегра-
лом
содер>кит еще
добавочньтй
мнох(итель.
€мьтсл второго
члена
уравнения
(98)
будет ясен и3
дальнейтшего.
Бсли проанали3ировать
полученное
ре|шение,
то сразу
видно' что
для
значений г, стремящихся к
;,0, оно переходит
в
ре1пение
предьтдущей
3адачи
для
дифузии
к
плоскому
электроду.
Физически
это о3начает' что
на очень близких
расстояниях
к
сферинеской поверхности
ее мох{но
рас_
сматривать
как
плоский
электрод.
||ри этом'
конечно'
понятие
близкого
расстояния
к поверхности
сферьт
о3начает
расстояние
малое посравнению
с
радиусом
криви3ны. Ба
расстояниях
не очень
маль]х посравнениюс
ра3-
мерами
сферь:, явления
диффузии
будут 3аметно
отличаться
от
той кар-
тиньт'
которая
устанавливается
на
плоском
электроде. Фсобенно
четко
вьтявится
ра3личие
ме)кду
ре1пением
для
плоского
электрода
и
для
сфери_
ческого
электрода' если сравнивать
соответствующие
величинь|
тока
диффузии. [ифференшируя
уравнение
(93)
по
г'
\1аход|1м
|_то
21г
о[
-
*:_2ц. [ е-у2ёш*
0г
г{;
)
" "3
1
0
(г_то)з
2г6со 1
^--|[{_,сг'
г|т
2уо|
1ри г:
|о 9\а-
прои3водная принимает
значение
т,0с\
9о
,
ф
\Б,/':"':
\/1ы*
т'
(ээ)
(99а)
Фтсюда
величина
тока
дифузии
(в
электринеских
единицах)
равна
!:пР|со1_д+1\.
1у;п+Б|'
(100)
3то вьтрах<ение
такх{е
состоит
и3
двух
слагаемь|х'
причем
первое
сла-
гаемое
точно соответствует
вь1ражению
для
тока
дифу3и14
к
плоской
по_
верхности
(см.
уравнение
93).
3то слагаемое
умень1пается
обратно
пропорционально
корн}о
квадратному
из
времени.
Бторое
слагаемое
для
величины
тока
является постоянной
величиной и от времени
не
зависит.
€оотно:пение
мех{ду
двумя
слагаемь|ми
уравнения
(
1
00)
3ависит
от
3
1{а
_
чения времени
/.
Б
начальные
моменты времени' когда [
мало,
первое сла-
гаемое
3начительно превосходит
второе, и
дифузия
к поверхности
капли
происходит
по тем )ке
закономерностям'
которые
имеют место
для диф_
фузии
к плоской поверхности.
|{ри.увеличении
значений /
первь:й
нлен
убьтвает,
и относительная
доля
тока, обусловленная вторь|м
членом'
во3_
растает.
|1ри
дальнейш:ем
во3растании времени ток стремится
не к нулю,
как
в
слунае
дифузии
к плоской
поверхност|\
а
к постоянной
величине
.
пРФсо
|:;,1.
€.
дифузия
переходит
из нестационарного
в
стационарное
состояние.
}1ох<но
показать'
что
установление
стационарного
состояния
диф_
фузии
с ве]1ичиной
тока
дифузии,
отличной от нуля' свя3ано
не со сфе-
ринеской фрмой
электрода'
а
с его конечньтми
]линейными
размерайи.
8сли
бы
мы
в
предыА}щем
параграфе
взяли
не
бесконенну:о плосйость,
а
дпск'
или вообще какое-либо
тФ1о опреде.,тенных
ра3меров'
находящееся
в неограциченной
однородной
среде'
то мь1
бьт такх<е на6лтодалп постепен_
нь:й
переход
от
нестационарной
дифузии
к стационарному состоянию.
ю
