Griffiths D. Head First Statistics
Подождите немного. Документ загружается.


you are here 4 151
calculating probabilities
S
A
B
S
A
B
S
A
B
P(A ∩ B) + P(A ∩ B
I
)
P(A
I
∩ B
I
)
P(A ∪ B) - P(B)
BE the probability
Your job is to play like you’re the
probability and shade in the area
that represents each of the following
probabilities on the Venn
diagrams.
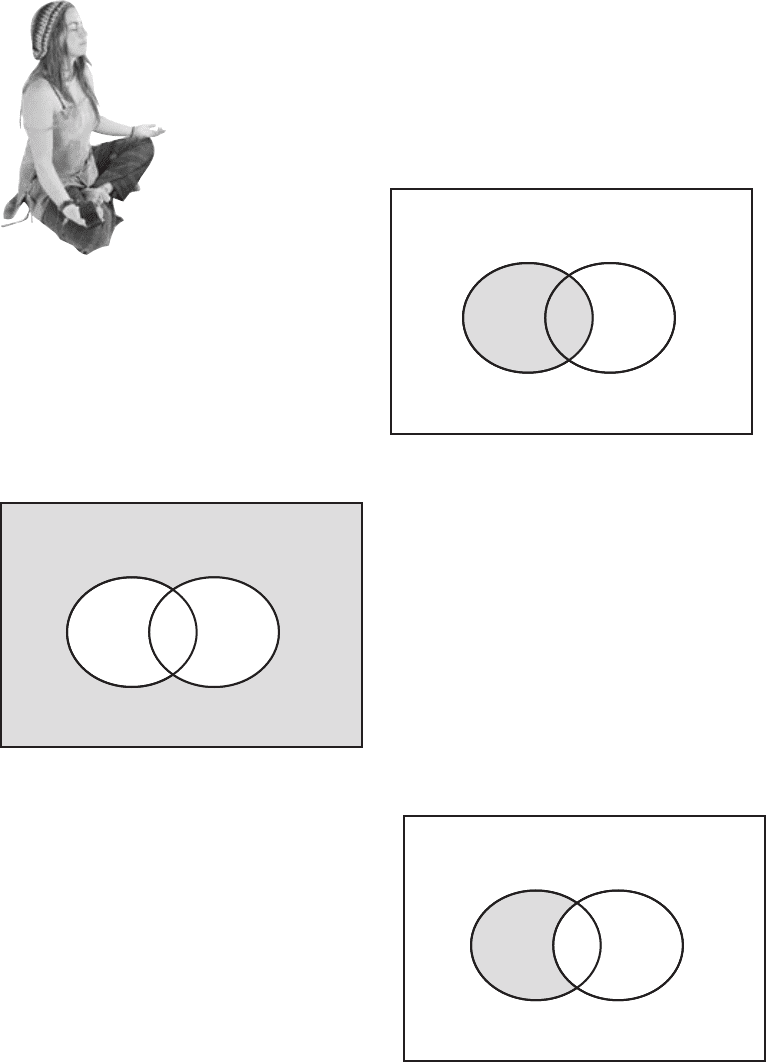
152 Chapter 4
S
A B
S
A B
S
A B
P(A ∩ B) + P(A ∩ B
I
)
P(A
I
∩ B
I
)
P(A ∪ B) - P(B)
BE the probability Solution
Your job was to play like you’re the probability
and shade in the area that represents each of
the probabilities on the Venn diagrams.
be the probability solution

you are here 4 153
calculating probabilities
50 sports enthusiasts at the Head First Health Club are asked whether they play baseball,
football, or basketball. 10 only play baseball. 12 only play football. 18 only play basketball. 6 play
baseball and basketball but not football. 4 play football and basketball but not baseball.
Draw a Venn diagram for this probability space. How many enthusiasts play baseball in total?
How many play basketball? How many play football?
Are any sports’ rosters mutually exclusive? Which sports are exhaustive (fill up the possibility
space)?
A or B
To find the probability of getting event
A or B, use
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
∪ means OR
∩ means AND
Vital StatisticsVital Statistics
154 Chapter 4
50 sports enthusiasts at the Head First Health Club are asked whether they play baseball, football
or basketball. 10 only play baseball. 12 only play football. 18 only play basketball. 6 play baseball
and basketball but not football. 4 play football and basketball but not baseball.
Draw a Venn diagram for this probability space. How many enthusiasts play baseball in total? How
many play basketball? How many play football?
Are any sports’ rosters mutually exclusive? Which sports are exhaustive (fill up the possibility
space)?
This information
looks complicated,
but drawing a
Venn diagram
will help us to
visualize what’s
going on.
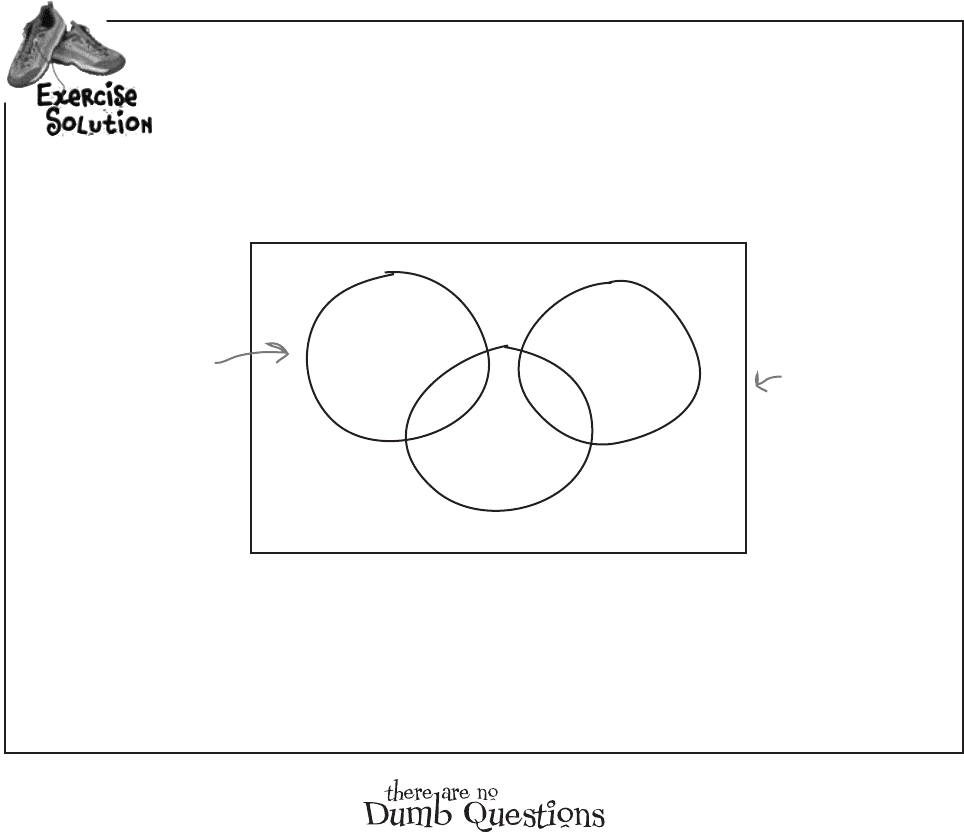
By adding up the values in each circle in the Venn diagram, we can determine that there
are 16 total baseball players, 28 total basketball players, and 16 total football players.
The baseball and football events are mutually exclusive. Nobody plays both baseball and
football, so P(Baseball ∩ Football) = 0
The events for baseball, football, and basketball are exhaustive. Together, they fill the
entire possibility space, so P(Baseball ∪ Football ∪ Basketball) = 1
Q:
Are A and A
I
mutually exclusive or
exhaustive?
A: Actually they’re both. A and A
I
can
have no common elements, so they are
mutually exclusive. Together, they make
up the entire possibility space so they’re
exhaustive too.
Q:
Isn’t P(A ∩ B) + P(A ∩ B
I
) just a
complicated way of saying P(A)?
A: Yes it is. It can sometimes be useful
to think of different ways of forming the
same probability, though. You don’t always
have access to all the information you’d
like, so being able to think laterally about
probabilities is a definite advantage.
Q:
Is there a limit on how many events
can intersect?
A: No. When you’re referring to the
intersection between several events, use
more
∩‘s. As an example, the intersection of
events A, B, and C is A
∩ B ∩ C.
Finding probabilities for multiple
intersections can sometimes be tricky. We
suggest that if you’re in doubt, draw a Venn
diagram and take a good, hard look at which
probabilities need to be added together and
which need to be subtracted.
S
Baseball
Football
Basketball
10
12
18
4
6
The numbers we’ve
been given all add
up to 50, the
total number of
sports lovers.
exercise solution

you are here 4 155
calculating probabilities
…but it’s time for another bet
Even with the odds in our favor, we’ve been unlucky with the outcomes at
the roulette table. The croupier decides to take pity on us and offers a little
inside information. After she spins the roulette wheel, she’ll give us a clue
about where the ball landed, and we’ll work out the probability based on
what she tells us.
Here’s your next
bet…and a hint about
where the ball landed.
Shh, don’t tell Fat Dan...
Bet: Even
Clue: The ball
landed in a
black pocket
Another unlucky spin…
We know that the probability of the ball landing on black or even
is 0.684, but, unfortunately, the ball landed on 23, which is red and
odd.
Should we take this bet?
How does the probability of getting even given that
we know the ball landed in a black pocket compare
to our last bet that the ball would land on black or
even. Let’s figure it out.

156 Chapter 4
108 10
108 810
Conditions apply
The croupier says the ball has landed in a black pocket.
What’s the probability that the pocket is also even?
S
Black Even
12
We already know
the pocket is black.
We want the probability
that the pocket is even,
given that it’s black.
But we’ve
already done this;
it’s just the probability of
getting black and even.
This is a slightly different problem
We don’t want to find the probability of getting a pocket
that is both black and even, out of all possible pockets.
Instead, we want to find the probability that the pocket is
even, given that we already know it’s black.
We can ignore these
areas—we know that
the pocket is black.
In other words, we want to find out how many pockets
are even out of all the black ones. Out of the 18 black
pockets, 10 of them are even, so
Black
Even
P(Even giv
en Black) = 10
18
= 0.556 (to 3 decimal places)
10 out of
18 are even.
introducing conditional probability
It turns out that even with some inside information, our odds are
actually lower than before. The probability of even given black is
actually less than the probability of black or even.
However, a probability of 0.556 is still better than 50% odds, so
this is still a pretty good bet. Let’s go for it.

you are here 4 157
calculating probabilities
P(A | B) = P(A ∩ B)
P(B)
S
B A
I’m a given
P(A ∩ B)
P(B)
We can rewrite this equation to give us a way of finding P(A ∩ B)
P(A ∩ B) = P(A | B)
×
P(B)
It doesn’t end there. Another way of writing P(A ∩ B) is P(B ∩ A).
This means that we can rewrite the formula as
P(B ∩ A) = P(B | A)
×
P(A)
In other words, just flip around the A and the B.
Find conditional probabilities
So how can we generalize this sort of problem? First of
all, we need some more notation to represent conditional
probabilities, which measure the probability of one event
occurring relative to another occurring.
If we want to express the probability of one event happening
given another one has already happened, we use the “|” symbol
to mean “given.” Instead of saying “the probability of event A
occurring given event B,” we can shorten it to say
P(A | B)
So now we need a general way of calculating P(A | B). What
we’re interested in is the number of outcomes where both A and
B occur, divided by all the B outcomes. Looking at the Venn
diagram, we get:
It looks like it can be difficult to show
conditional probability on a Venn diagram.
I wonder if there’s some other way.
Venn diagrams aren’t always the best way of
visualizing conditional probability.
Don’t worry, there’s another sort of diagram you can use—a
probability tree.
Because we’re trying to find the
probability of A given B, we’re only
interested in the set of events
where B occurs.
The probability of A given
that we know B has happened.
158 Chapter 4
It’s not always easy to visualize conditional probabilities with
Venn diagrams, but there’s another sort of diagram that really
comes in handy in this situation—the probability tree.
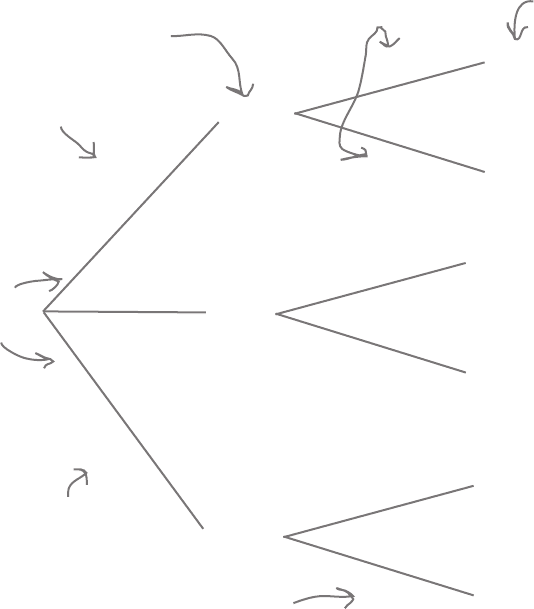
Here’s a probability tree for our problem with the roulette
wheel, showing the probabilities for getting different colored
and odd or even pockets.
Black
Red
Green
Even
Odd
Even
Odd
00
0
18/38
18/38
2/38
8/18
8/18
10/18
10/18
1/2
1/2
These are branches,
like the branches
of a tree.
Here are the first set of
exclusive events, the colors. The
probabilities for each event go
along the relevant branch.
These are all the
second set of events.
The probabilities for
each set of branches
must add up to 1.
P(Green)
P(00 | Green)
The first set of branches shows the probability of each
outcome, so the probability of getting a black is 18/38, or
0.474. The second set of branches shows the probability
of outcomes given the outcome of the branch it is
linked to. The probability of getting an odd pocket given
we know it’s black is 8/18, or 0.444.
probability trees
You can visualize conditional probabilities with a probability tree
you are here 4 159
calculating probabilities
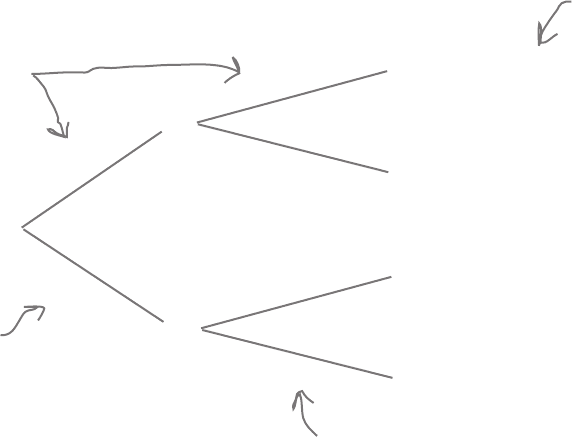
B
A
P(B)
P(A | B)
Probability trees don’t just help you visualize probabilities; they can help
you to calculate them, too.
Let’s take a general look at how you can do this. Here’s another
probability tree, this time with a different number of branches. It shows
two levels of events: A and A
I
and B and B
I
. A
I
refers to every possibility
not covered by A, and B
I
refers to every possibility not covered by B.
You can find probabilities involving intersections by multiplying the
probabilities of linked branches together. As an example, suppose you
want to find P(A ∩ B). You can find this by multiplying P(B) and P(A | B)
together. In other words, you multiply the probability on the first level B
branch with the probability on the second level A branch.
P(A ∩ B) = P(A | B)
×
P(B)
B
I
A
I
P(A
I
| B)
P(A
I
∩ B) = P(A
I
| B)
×
P(B)
A
P(A | B
I
)
P(A ∩ B
I
) = P(A | B
I
)
×
P(B
I
)
A
I
P(A
I
| B
I
)
P(A
I
∩ B
I
) = P(A
I
| B
I
)
×
P(B
I
)
P(B
I
)
To find P(A
∩
B), just multiply
the probabilities for these two
branches together.
The probability of not
getting A given that B
hasn’t happened
This is the same equation you
saw earlier—just multiply the
adjoining branches together.
The probability of
not getting event B
Using probability trees gives you the same results you saw earlier, and
it’s up to you whether you use them or not. Probability trees can be time-
consuming to draw, but they offer you a way of visualizing conditional
probabilities.
Trees also help you calculate conditional probabilities
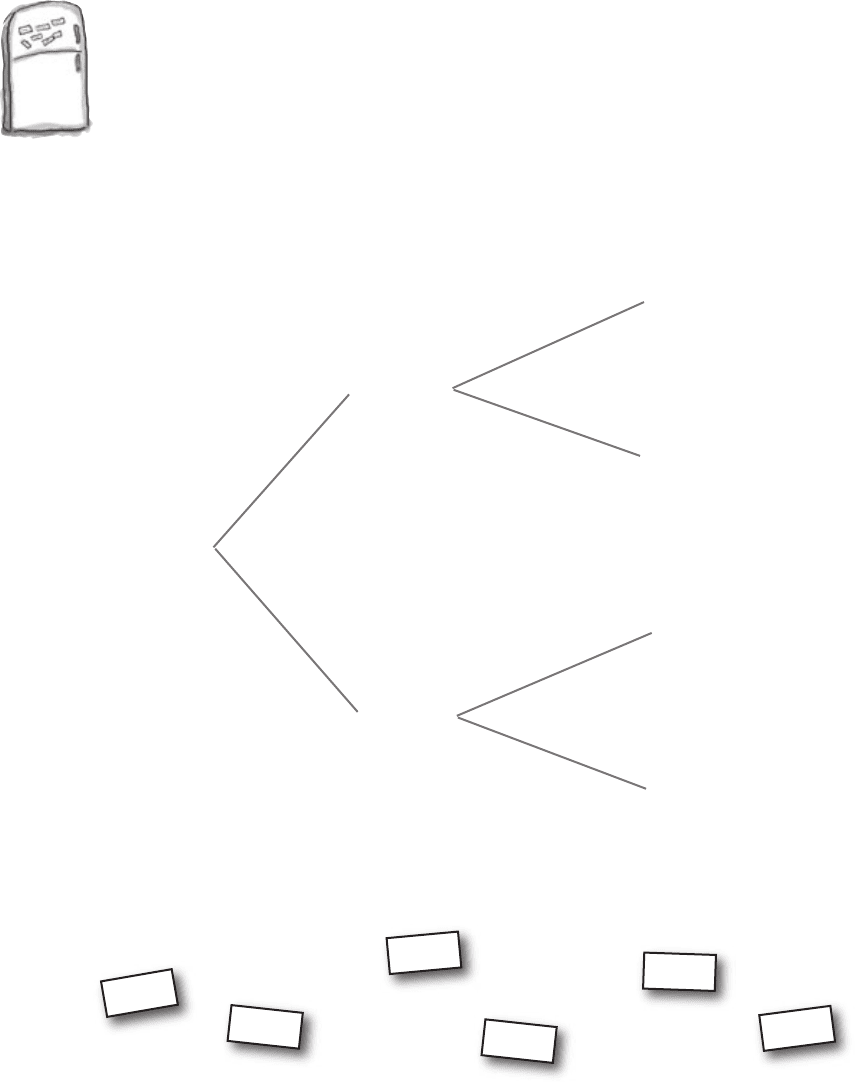
160 Chapter 4
Donuts
Coffee
Donuts
I
Coffee
I
Coffee
Coffee
I
Probability Magnets
Duncan’s Donuts are looking into the probabilities of their customers buying
donuts and coffee. They drew up a probability tree to show the probabilities,
but in a sudden gust of wind, they all fell off. Your task is to pin the
probabilities back on the tree. Here are some clues to help you.
3/4
1/4
2/5
3/5
1/3
2/3
P(Donuts) = 3/4 P(Coffee | Donuts
I
) = 1/3 P(Donuts ∩ Coffee) = 9/20
probability magnets
