Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 121

measuring variability and spread

Standard Scores Up Close

Standard scores work by transforming sets of data into a new, theoretical distribution

with a mean of 0 and a standard deviation of 1. It’s a generic distribution that can

be used for comparisons. Standard scores effectively transform your data so that it

fits this model while making sure it keeps the same basic shape.

Standard scores can take any value, and they indicate position relative to the mean.

Positive z-scores mean that your value is above the mean, and negative z-scores

mean that your value is below it. If your z-score is 0, then your value is the mean

itself. The size of the number shows how far away the value is from the mean.

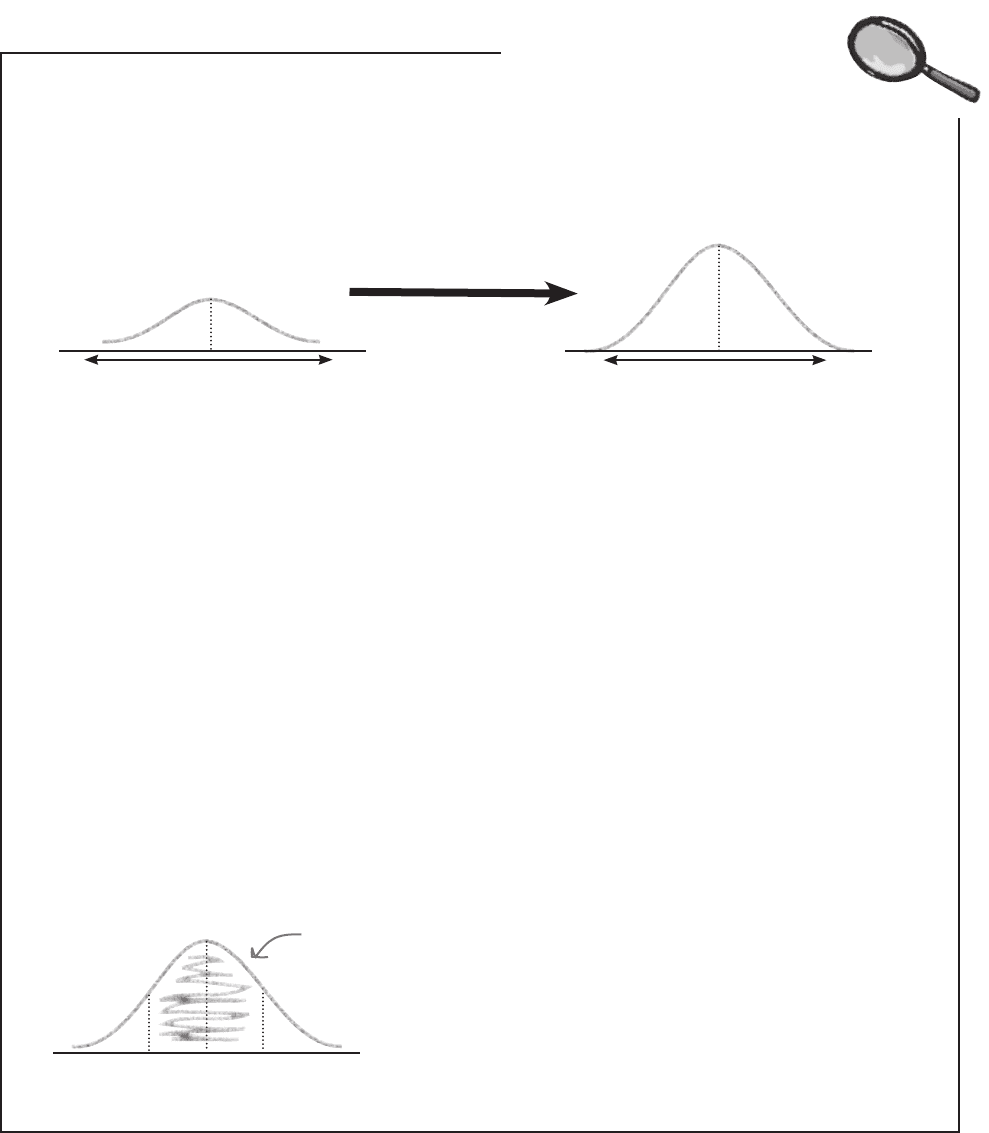
Standard deviations from the mean

Sometimes statisticians express the relative position of a particular value in terms

of standard deviations from the mean. As an example, a statistician may

say that a particular value is within 1 standard deviation of the mean. It’s really

just another way of indicating how close values are to the mean, but what does it

mean in practice?

We’ve seen that using z-scores transforms your data set into a generic distribution

with a mean of 0 and a standard deviation of 1. If a value is within 1 standard

deviation of the mean, this tells us that the standard score of the value is between

-1 and 1. Similarly, if a value is within 2 standard deviations of the mean, the

standard score of the value would be somewhere between -2 and 2.

Standard

score = number

of standard

deviations from

the mean.

μ = 0

σ = 1

-1 0 1

If a value is within 1 standard

deviation of the mean, it’s

within this area here—the

central part of the data.

122 Chapter 3

The variance and standard deviation measure

how values are dispersed by looking at how far

values are from the mean.

The variance is calculated using

An alternate form is



The standard deviation is equal to the square root

of the variance, and the variance is the standard

deviation squared.

Standard scores, or z-scores, are a way of

comparing values across different sets of data

where the means and standard deviations are

different. To find the standard score of a value x,

use:



So variance and standard deviation both measure the

spread of your data. How are they different from the range?

A: The range is quite a simplistic measure of the spread of your

data. It tells you the difference between the highest and lowest

values, but that’s it. You have no way of knowing how the data is

clustered within it.

The variance and standard deviation are a much better way

of measuring the variability of your data and how your data is

dispersed, as they take into account how the data is clustered.

They look at how far values typically are from the center of

your data.

And what’s the difference between variance and

standard deviation? Which one should I use?

A: The standard deviation is the square root of the variance,

which means you can find one from the other.

The standard deviation is probably the most intuitive, as it tells you

roughly how far your values are, on average, from the mean.

How do standard scores fit into all this?

A: Standard scores use the mean and standard deviation to

convert values in a data set to a more generic distribution, while at

the same time, making sure your data keeps the same basic shape.

They’re a way of comparing different values across different data

sets even when the data sets have different means and standard

deviations. They’re a way of measuring relative standing.

Do standard scores have anything to do with detecting

outliers?

Good question! Determining outliers can be subjective, but

sometimes outliers are defined as being more than 3 standard

deviations of the mean. Statisticians have different opinions about

this though, so be warned.

no dumb questions

- )

z =

you are here 4 123

measuring variability and spread

Complete the table below. Name each type of measure of dispersion we’ve encountered

in the chapter, and show how to calculate it. Try your hardest to fill this out without

looking back through the chapter.

Statistic How to calculate

Range

Upper quartile - Lower quartile

Standard Deviation (σ)

Standard Score

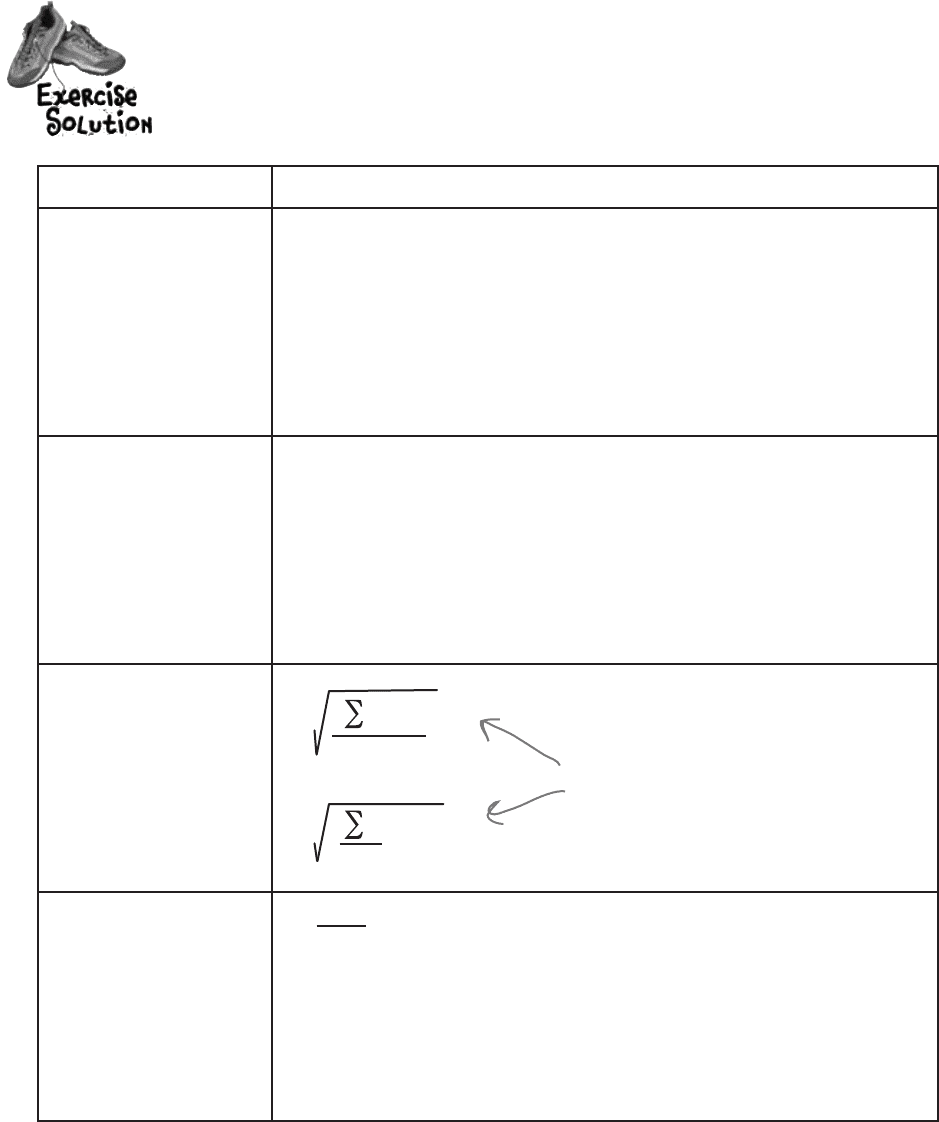
124 Chapter 3

Complete the table below. Name each type of measure of dispersion we’ve encountered

in the chapter, and show how to calculate it. Try your hardest to fill this out without

looking back through the chapter.

Statistic How to calculate

Range

Upper bound - Lower bound

Interquartile range

Upper quartile - Lower quartile

Standard Deviation (σ)

(x - μ)

Standard Score

z = x - μ

Both of these give

the same result.

exercise solution

- μ

you are here 4 125

measuring variability and spread

Let’s hear it for the

standard deviation,

our new team mascot!

Statsville All Stars win the league!

All the basketball matches for the season have now been played,

and the Statsville All Stars finished at the top of the league. You

clearly helped the coach pick the best player for the team.

Just remember: you owe it all to the friendly neighborhood

standard deviation.

this is a new chapter 127

calculating probabilities

Taking Chances

Life is full of uncertainty.

Sometimes it can be impossible to say what will happen from one minute to the

next. But certain events are more likely to occur than others, and that’s where

probability theory comes into play. Probability lets you predict the future by

assessing how likely outcomes are, and knowing what could happen helps you

make informed decisions. In this chapter, you’ll find out more about probability

and learn how to take control of the future!

What’s the probability he’s

remembered I’m allergic to

non-precious metals?

128 Chapter 4

Are you ready to play?

Fat Dan’s Grand Slam

Fat Dan’s Casino is the most popular casino in the

district. All sorts of games are offered, from roulette

to slot machines, poker to blackjack.

It just so happens that today is your lucky day. Head

First Labs has given you a whole rack of chips to

squander at Fat Dan’s, and you get to keep any

winnings. Want to give it a try? Go on—you know

you want to.

These are all your poker

chips; looks like you’re in

for a fun time.

There’s a lot of activity over at the roulette wheel,

and another game is just about to start. Let’s see

how lucky you are.

One of Fat Dan’s croupiers

welcome to fat dan’s casino

you are here 4 129

calculating probabilities

Roll up for roulette!

You’ve probably seen people playing roulette in movies even

if you’ve never tried playing yourself. The croupier spins a

roulette wheel, then spins a ball in the opposite direction, and

you place bets on where you think the ball will land.

The roulette wheel used in Fat Dan’s Casino has 38 pockets

that the ball can fall into. The main pockets are numbered

from 1 to 36, and each pocket is colored either red or black.

There are two extra pockets numbered 0 and 00. These

pockets are both green.

You can place all sorts of bets with roulette. For instance,

you can bet on a particular number, whether that number

is odd or even, or the color of the pocket. You’ll hear more

about other bets when you start playing. One other thing to

remember: if the ball lands on a green pocket, you lose.

Roulette boards make it easier to keep track of which

numbers and colors go together.

Lightest gray = green

black = black,

medium gray = red,

Roulette wheel

Roulette board. (See

page 130 for a larger

version.)

You place bets on the

pocket the ball will

fall into on the wheel

using the board.

If the ball falls

into the 0 or 00

pocket, you lose!

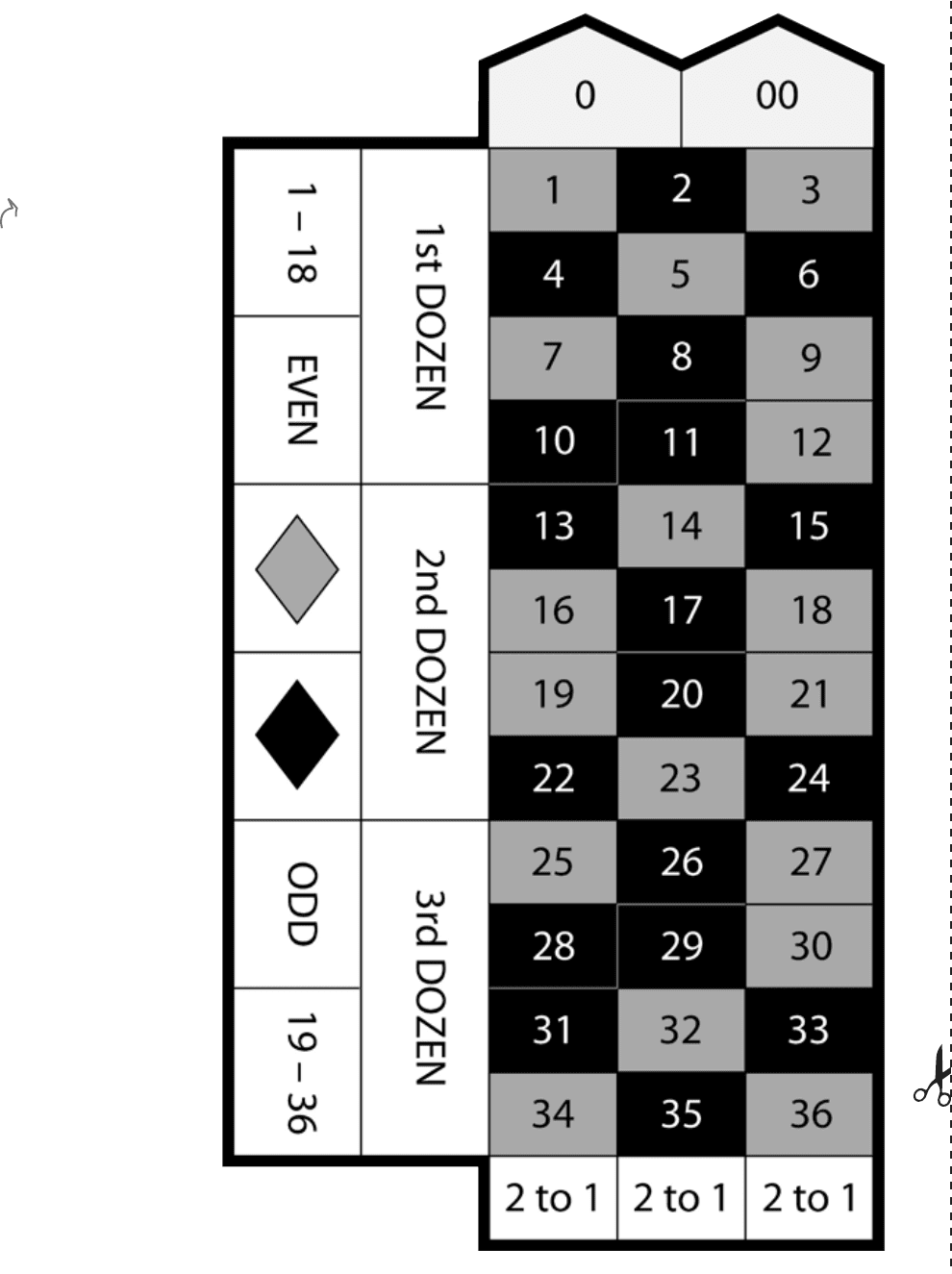
130 Chapter 4

Your very own roulette board

You’ll be placing a lot of roulette bets in this chapter.

Here’s a handy roulette board for you to cut out and

keep. You can use it to help work out the probabilities in

this chapter.

roulette board

Just be careful with those scissors.