Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 141

calculating probabilities

That’s a lot of pockets to

count. We’ve already worked out

P(Black) and P(Green). Maybe we

can use one of these instead.

We can use the probabilities we already

know to work out the one we don’t know.

Take a look at your roulette board. There are only three

colors for the ball to land on: red, black, or green. As we’ve

already worked out what P(Green) is, we can use this value to

find our probability without having to count all those black

and red pockets.

P(Black or Red) = P(Green

)

= 1 - P(Green)

= 1 - 0.053

= 0.947 (to 3 decimal places)

Don’t just take our word for it. Calculate the probability of getting

a black or a red by counting how many pockets are black or red

and dividing by the number of pockets.

Let’s look at the probability of an event that should be more

likely to happen. Instead of betting that the ball will land in

a black pocket, let’s bet that the ball will land in a black or a

red pocket. To work out the probability, all we have to do is

count how many pockets are red or black, then divide by the

number of pockets. Sound easy enough?

Let’s bet on an even more likely event

Bet:

Red or Black

142 Chapter 4

Black

Red

Don’t just take our word for it. Calculate the probability of getting

a black or a red by counting how many pockets are black or red

and dividing by the number of pockets.

P(Black or Red) = 36

= 0.947 (to 3 decimal places)

So P(Black or Red) = 1- P(Green)

You can also add probabilities

There’s yet another way of working out this sort of

probability. If we know P(Black) and P(Red), we can find

the probability of getting a black or red by adding these two

probabilities together. Let’s see.

A pocket can’t be both

black and red; they’re

separate events.

P(Black or Red) = 18 + 18

= 18 + 18

38 38

= P(Black) + P(Red)

In this case, adding the probabilities gives exactly

the same result as counting all the red or black

pockets and dividing by 38.

Adding the probabilities gives

the same result as adding

the number of black or red

pockets and dividing by 38.

S is the possibility

space, the box

containing all the

possibilities

Two of the pockets are

neither red nor black, so

we’ve put 2 out here.

adding probabilities

you are here 4 143

calculating probabilities

It looks like there are three ways of dealing with this sort

of probability. Which way is best?

A: It all depends on your particular situation and what information

you are given.

Suppose the only information you had about the roulette wheel was

the probability of getting a green. In this situation, you’d have to

calculate the probability by working out the probability of not getting

a green:

- P(Green)

On the other hand, if you knew P(Black) and P(Red) but didn’t know

how many different colors there were, you’d have to calculate the

probability by adding together P(Black) and P(Red).

So I don’t have to work out probabilities by counting

everything?

A: Often you won’t have to, but it all depends on your situation. It

can still be useful to double-check your results, though.

If some events are so unlikely to happen, why do people

bet on them?

A: A lot depends on the sort of return that is being offered. In

general, the less likely the event is to occur, the higher the payoff

when it happens. If you win a bet on an event that has a high

probability, you’re unlikely to win much money. People are tempted to

make bets where the return is high, even though the chances of them

winning is negligible.

Does adding probabilities together like that always work?

A: Think of this as a special case where it does. Don’t worry, we’ll

go into more detail over the next few pages.

Probability

To find the probability of an

event A, use

P(A) = n(A)

n(S)

Vital StatisticsVital Statistics

is the complementary event of

A. It’s the probability that event

A does not occur.

P(A

) = 1 - P(A)

Vital StatisticsVital Statistics

144 Chapter 4

Bet:

Black or Even

You win!

This time the ball landed in a red pocket, the number 7, so

you win some chips.

That’s easy. We just

add the black and even

probabilities together.

Sometimes you can add together

probabilities, but it doesn’t work in

all circumstances.

We might not be able to count on being able to do

this probability calculation in quite the same way

as the previous one. Try the exercise on the next

page, and see what happens.

This time, you picked a

winning pocket: a red one.

Time for another bet

Now that you’re getting the hang of calculating

probabilities, let’s try something else. What’s the

probability of the ball landing on a black or even pocket?

a new bet

you are here 4 145

calculating probabilities

Let’s find the probability of getting a black or even

(assume 0 and 00 are not even).

1. What’s the probability of getting a black?

2. What’s the probability of getting an even number?

3. What do you get if you add these two probabilities together?

4. Finally, use your roulette board to count all the holes that are either black or even, then divide

by the total number of holes. What do you get?

146 Chapter 4

Let’s find the probability of getting a black or even (assume 0 and

00 are not even).

1. What’s the probability of getting a black?

2. What’s the probability of getting an even number?

3. What do you get if you add these two probabilities together?

4. Finally, use your roulette board to count all the holes that are either black or even, then divide by

the total number of holes. What do you get?

18 / 38 = 0.474

0.947

26 / 38 = 0.684

Uh oh! Different answers

I don’t get it. Adding

probabilities worked OK last

time. What went wrong?

Let’s take a closer look...

sharpen solution

you are here 4 147

calculating probabilities

What sort of effect do you think

this intersection could have

had on the probability?

Black

Even

Some of the pockets

are both black and even.

When we were working out the probability of the ball landing in a

black or red pocket, we were dealing with two separate events, the

ball landing in a black pocket and the ball landing in a red pocket.

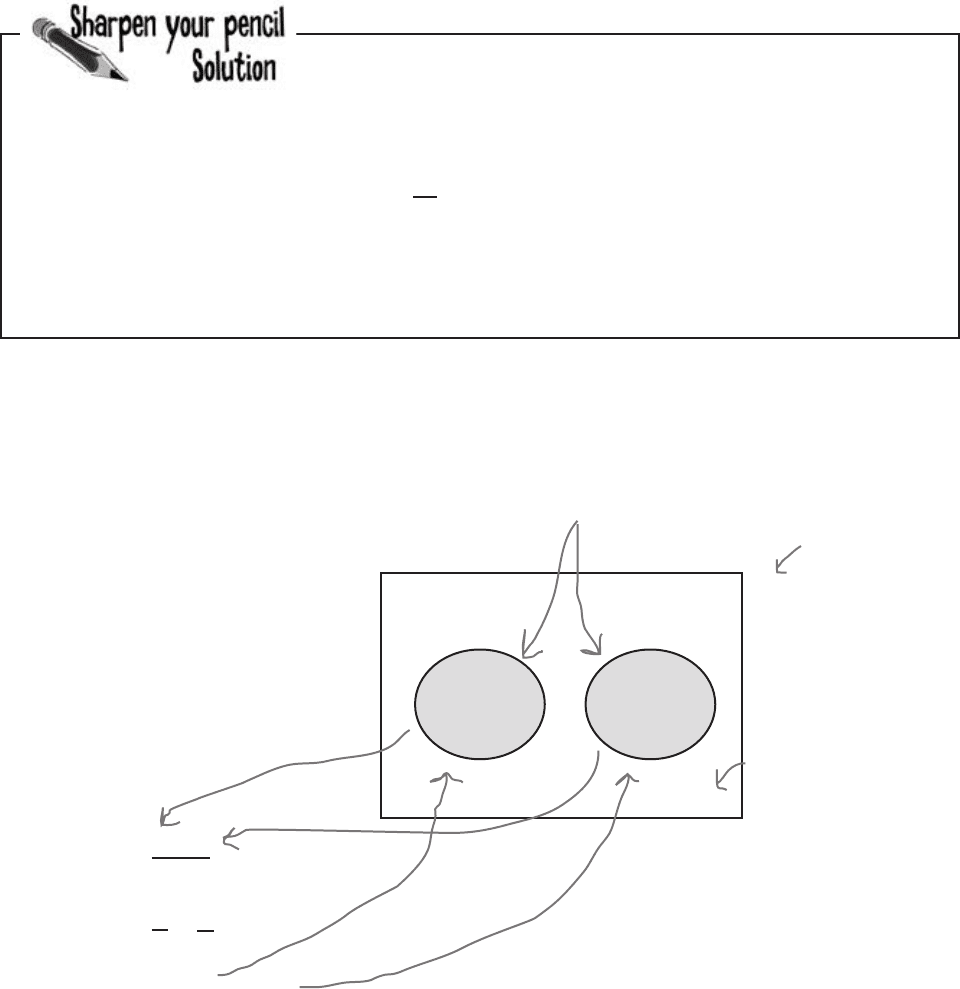
These two events are mutually exclusive because it’s impossible for

the ball to land in a pocket that’s both black and red.

Black

Red

We have absolutely

nothing in common.

We’re exclusive events.

What about the black and even events? This time the events

aren’t mutually exclusive. It’s possible that the ball could land in

a pocket that’s both black and even. The two events intersect.

I guess this means

we’re sharing

If two events

are mutually

exclusive, only

one of the two

can occur.

If two events

intersect, it’s

possible they

can occur

simultaneously.

Exclusive events and intersecting events

148 Chapter 4

108

Black

108

Black Even

810

108

Problems at the intersection

Calculating the probability of getting a black or even went

wrong because we included black and even pockets twice.

Here’s what happened.

First of all, we found the probability of getting a black

pocket and the probability of getting an even number.

Black

P(Black) = 18

= 0.474

Even

P(Even) = 18

= 0.474

When we added the two probabilities together, we

counted the probability of getting a black and even

pocket twice.

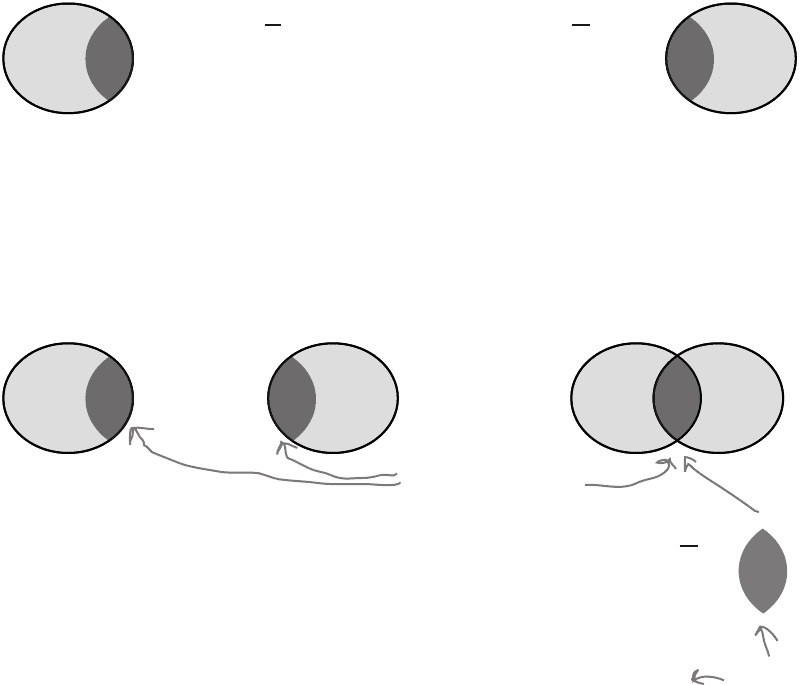
The intersection here

was included twice

To get the correct answer, we need to subtract the

probability of getting both black and even. This gives

We only need

one of these, so

let’s subtract

one of them.

P(Black or Even) = P(Black) + P(Even) - P(Black and Even)

Even

810

intersection and union

We can now substitute in the values we just calculated to find P(Black or Even):

P(Black or Even) = 18/38 + 18/38 - 10/38 = 26/38 = 0.684

P(Black ∩ Even) = 10

= 0.263

you are here 4 149

calculating probabilities

Some more notation

There’s a more general way of writing this using some

more math shorthand.

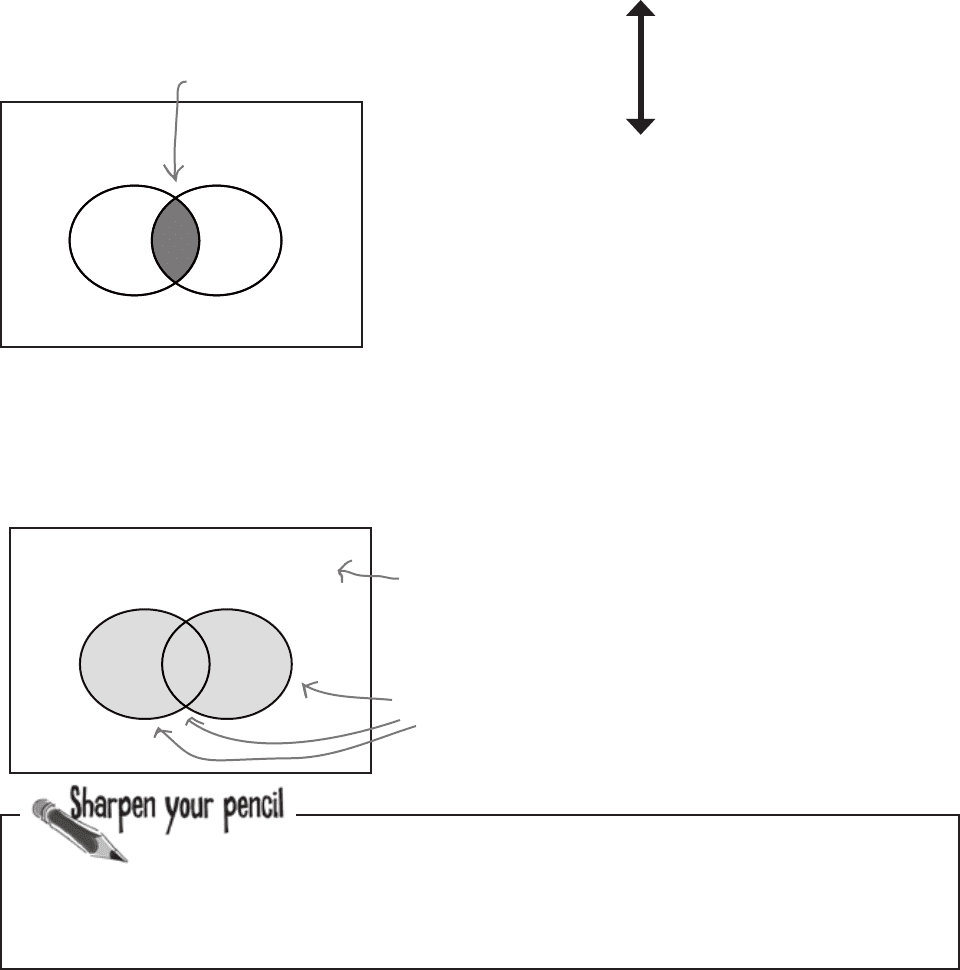
First of all, we can use the notation A ∩ B to refer to

the intersection between A and B. You can think of

this symbol as meaning “and.” It takes the common

elements of events.

A ∪ B, on the other hand, means the union of A and B.

It includes all of the elements in A and also those in B.

You can think of it as meaning “or.”

If A ∪ B =1, then A and B are said to be exhaustive.

Between them, they make up the whole of S. They

exhaust all possibilities.

i∩tersection

∪nion

On the previous page, we found that

(P(Black or Even) = P(Black) + P(Even) - P(Black and Even)

Write this equation for A and B using

∩ and ∪ notation.

The entire shaded

area is A ∪ B.

The intersection

here is A ∩ B.

If there are no elements that aren’t

in either A, B, or both, like in this

diagram, then A and B are exhaustive.

Here the white bit is empty.

150 Chapter 4

P(A ∪ B) = P(A) + P(B) - P(A ∩ B)

On the previous page, we found that

(P(Black or Even) = P(Black) + P(Even) - P(Black and Even)

Write this equation for A and B using

∩ and ∪ notation.

P(A or B)

P(A and B)

It’s not actually that different.

Mutually exclusive events have no elements in common with each

other. If you have two mutually exclusive events, the probability of

getting A and B is actually 0—so P(A ∩ B) = 0. Let’s revisit our black-

or-red example. In this bet, getting a red pocket on the roulette wheel

and getting a black pocket are mutually exclusive events, as a pocket

can’t be both red and black. This means that P(Black ∩ Red) = 0, so

that part of the equation just disappears.

There’s a difference

between exclusive

and exhaustive.

If events A and B are

exclusive, then

P(A

∩ B) = 0

If events A and B are exhaustive, then

P(A

∪ B) = 1

So why is the equation for exclusive

events different? Are you just giving

me more things to remember?

sharpen solution