Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 301

These formulae work for any

binomial distribution.

E(X) = np

Var(X) = npq

Binomial expectation and variance

Let’s summarize what we just did. First of all, we took at one trial, where

the probability of success is p, and where the distribution is binomial.

Using this, we found the expectation and variance of a single trial.

We then considered n independent trials, and used shortcuts to find the

expectation and variance of n trials. We found that if X ~ B(n, p),

This is useful to know as it gives us a quick way of finding the expectation

and variance of any probability distribution, without us having to work out

lots of individual probabilities.

The geometric distribution and the

binomial distribution seem similar. What’s

the difference between them? Which one

should I use when?

A: The geometric and binomial

distributions do have some things

in common. Both of them deal with

independent trials, and each trial can result

in success or failure. The difference between

them lies in what you actually need to find

out, and this dictates which probability

distribution you need to use.

If you have a fixed number of trials and you

want to know the probability of getting a

certain number of successes, you need to

use the binomial distribution. You can also

use this to find out how many successes you

can expect to have in your n trials.

If you’re interested in how many trials you’ll

need before you have your first success,

then you need to use the geometric

distribution instead.

The geometric distribution has a

mode. Does the binomial distribution?

A: Yes, it does. The mode of a probability

distribution is the value with the highest

probability. If p is 0.5 and n is even, the

mode is np. If p is 0.5 and n is odd it has two

modes, the two values either side of np. For

other values of n and p, finding the mode is

a matter of trial and error, but it’s generally

fairly close to np.

So for both the geometric and the

binomial distributions you run a series

of trials. Does the probability of success

have to be the same for each trial?

A: In order for the geometric or binomial

distribution to be applicable, the probability

of success in each trial must be the same.

If it’s not, then neither the geometric nor

binomial distribution is appropriate.

I’ve tried calculating E(X) and

it’s not a value that’s in the probability

distribution. Did I do something wrong?

A: When you calculate E(X), the result

may not be a possible value in your

probability distribution. It may not be a value

that can actually occur. If you get a result

like this, it doesn’t mean that you’ve made a

mistake, so don’t worry.

Are there any other sorts of

probability distribution?

A: Yes, there are. Keep reading and you’ll

find out more.

302 WHO WANTS TO WIN A SWIVEL CHAIR

Your quick guide to the binomial distribution

Here’s a quick summary of everything you could possibly need to know about the binomial distribution

When do I use it?

Use the binomial distribution if you’re running a fixed number of independent trials, each one can have a success

or failure, and you’re interested in the number of successes or failures

How do I calculate probabilities?

Use

What about the expectation and variance?

E(X) = np

Var(X) = npq

P(X = r) =

n - r

= n!

r! (n - r)!

where p is the probability of success in a trial, q = 1 - p, n is the number of trials, and X is the number of

successes in the n trials.

you are here 4 303

In the latest round of Who Wants To Win A Swivel Chair, there are 5 questions. The probability of

getting a successful outcome in a single trial is 0.25

1. What’s the probability of getting exactly two questions right?

4. What’s the probability of getting no questions right?

2. What’s the probability of getting exactly three questions right?

5. What are the expectation and variance?

3. What’s the probability of getting two or three questions right?

304 WHO WANTS TO WIN A SWIVEL CHAIR

In the latest round of Who Wants To Win A Swivel Chair, there are 5 questions. The probability of

getting a successful outcome in a single trial is 0.25

1. What’s the probability of getting exactly two questions right?

If X represents the number of questions answered correctly, then X ~ B(n, p)

P(X = 2) =

x 0.25

x 0.75

= 5! x 0.0625 x 0.421875

3!2!

= 10 x 0.0264

= 0.264

4. What’s the probability of getting no questions right?

P(X = 0) = 0.75

= 0.237

2. What’s the probability of getting exactly three questions right?

P(X = 3) =

x 0.25

x 0.75

= 5! x .0.015625 x 0.5625

2!3!

= 10 x 0.00879

= 0.0879

5. What are the expectation and variance?

E(X) = np

= 5 x 0.25

= 1.25

3. What’s the probability of getting two or three questions right?

P(X = 2 or X = 3) = P(X = 2) + P(X = 3)

= 0.264 + 0.0879

= 0.3519

Var(X) = npq

= 5 x 0.25 x 0.75

= 0.9375

So, you can

expect to get

less than 2 questions

correct? I think now’s

about time to quit.

Sorry you won’t win the

swivel chair, though.

you are here 4 305

Here are the questions for Round Two. The questions are all about

the game show host.

D: Releasing an album

B: Winning Mr Statsville 2008

C: Raising $1000 for the seal sanctuary

3. What is his greatest achievement?

A: Hosting a quiz show

D: A hovercraft

B: A tin dog

C: A horse

2. What would be an ideal gift for him?

A: A statue

D: May

B: Marie

C: Maggie

1. What was the name of his first girlfriend?

A: Mary

D: To have his own hair care range

B: To release an exercise DVD

C: To launch his own range of menswear

4. What is his secret ambition?

A: To launch a range of sports equipment

D: 2008

B: 2006

C: 2007

5. In what year was he abducted by aliens?

A: 2005

It’s been great having you as a contestant on the

show, and we’d love to have you back later on. But

we’ve just had a phone call from the Statsville

cinema. Some problem about popcorn...?

306 Chapter 7

So how do we find probabilities?

The trouble with this sort of problem is that while we know the mean

number of popcorn machine malfunctions per week, the actual number

of breakdowns varies each week. On the whole we can expect 3 or 4

malfunctions per week, but in a bad week there’ll be far more, and in a good

week there might be none at all.

We need to find the probability that the popcorn machine won’t break down

next week.

Sound difficult? Don’t worry, there’s a probability distribution that’s

designed for just this sort of situation. It’s called the Poisson distribution.

Where’s my popcorn?

I want popcorn now!

Give me my popcorn!

The Statsville Cinema has a problem

It’s a fact of life that cinemagoers like popcorn.

The trouble is that the popcorn machine at the Statsville Cinema keeps

breaking down, and the customers aren’t happy.

The cinema has a big promotion on next week, and the cinema manager

needs everything to be perfect. He doesn’t want the popcorn machine to

break down during the week, or people won’t come back.

The mean number of popcorn machine malfunctions per week, or rate of

malfunctions, is 3.4. What’s the probability that it won’t break down at all

next week?

If they expect the machine to break down more than a few times next week,

the Statsville Cinema will buy a new popcorn machine, but if not, they’ll

stick with the current one and run the risk of a breakdown.

It’s a different sort of distribution

This is a different sort of problem from the ones we’ve encountered so far.

This time there’s no series of attempts or trials. Instead, we have a situation

where we know the rate at which malfunctions happen, and where

malfunctions occur at random.

introducing the poisson distribution

you are here 4 307

geometric, binomial, and poisson distributions

Poisson Distribution Up Close

The Poisson distribution covers situations where:

Let’s use the variable X to represent the number of occurrences in

the given interval, for instance the number of breakdowns in a week. If

X follows a Poisson distribution with a mean of λ occurrences per interval

or rate, we write this as:

Individual ev

ents occur at random and independently in a given

interval. This can be an interval of time or space—for example,

during a week, or per mile.

You know the mean number of occurrences in the interval or the

rate of occurrences, and it’s finite. The mean number of occurrences

is normally represented by the Greek letter λ (lambda).

X ~ Po(λ)

P(X = r) = e

-λ

The formula for the probability uses the exponential function e

, where x

is some number. It’s a standard function available on most calculators, so

even though the formula might look daunting at first, it’s actually quite

straightforward to use in practice.

As an example, if X ~ Po(2)

We’re not going to derive it here, but to find the probability that there are r

occurrences in a specific interval, use the formula:

P(X = 3) = e

-2

= e

-2

= e

-2

1.333

= 0.180

Use the formula and substitute

in r = 3 and

= 2.

Don’t let appearances put you off.

It’s pretty straightforward to

calculate in practice.

So if X follows a Poisson distribution, what’s its expectation and variance?

It’s easier than you might think...

e is a mathematical

constant. It always

stands for 2.718, so you

can just substitute in

this number for e in the

Poisson formula. Many

scientific calculators

have an e

key that will

calculate powers of e

for you.

308 Chapter 7

E(X) = λ Var(X) = λ

Finding the expectation and variance for the Poisson distribution is a lot easier

than finding it for other distributions.

If X ~ Po(λ), E(X) is the number of occurrences we can expect to have in a

given intervals, so for the popcorn machine, it’s the number of breakdowns we

can expect to have in a typical week. In other words, E(X) is the mean number

of occurrences in the given interval.

Now, if X ~ Po(λ), then the mean number of occurrences is given by λ. In

other words, E(X) is equal to λ, the parameter that defines our Poisson

distribution.

To make things even simpler, the variance of the Poisson distribution is also

given by λ, so if X ~ Po(λ),

In other words, if you’re given a Poisson distribution Po(λ), you don’t have to

calculate anything at all to find the expectation and variance. It’s the parameter

of the Poisson distribution itself.

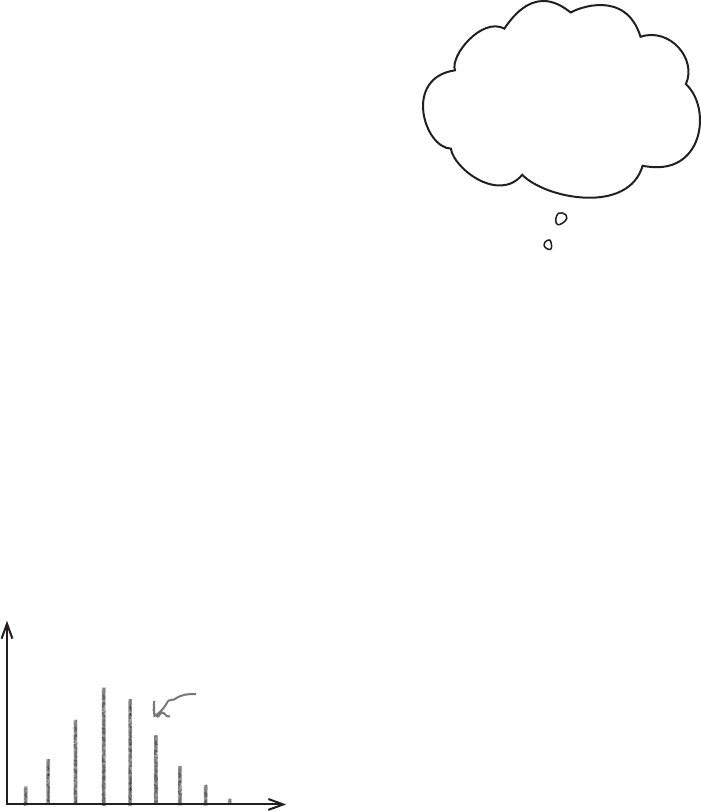
What does the Poisson distribution look like?

The shape of the Poisson distribution varies depending on the value of λ. If

λ is small, then the distribution is skewed to the right, but it becomes more

symmetrical as λ gets larger.

If λ is an integer, then there are two modes, λ and λ - 1. If λ is not an integer,

then the mode is λ.

The shape of the Poisson distribution

depends on the value of

P(X = x)

I tell you everything

you need to know about

the Poisson distribution.

Expectation, variance,

the lot.

Expectation and variance for the Poisson distribution

finding expectation and variance for poisson

you are here 4 309

geometric, binomial, and poisson distributions

BE the popcorn machine

Your job is to play like you’re

the popcorn machine and say

what the probability is of you

malfunctioning a particular

number of times next week.

Remember, the mean number of

times you break down in a week

is 3.4.

1. What’s the probability of the machine not malfunctioning next week?

2. What’s the probability of the machine malfunctioning three times next week?

3. What’s the expectation and variance of the machine malfunctions?

310 Chapter 7

1. What’s the probability of the machine not malfunctioning next week?

Let’s use X to represent the number of

times the popcorn machine malfunctions in

a week. We have

X ~ Po(3.4)

If there are no malfunctions, then X must be 0.

P(X = 0) = e

= e

-3.4

x 3.4

= e

-3.4

x 1

= 0.033

P(X = 3) = e

-3.4

x 3.4

= e

-3.4

x 39.304

= 0.033 x 6.55

= 0.216

2. What’s the probability of the machine malfunctioning three times next week?

3. What’s the expectation and variance of the machine malfunctions?

E(X) = λ

= 3.4

Var(X) =

= 3.4

Looks like we can

expect the machine to break

down only 3.4 times next week,

so we’ll risk it and skip that new

machine. Don’t tell the moviegoers.

be the popcorn machine solution

BE the popcorn machine solution

Your job is to play like you’re

the popcorn machine and say

what the probability is of you

malfunctioning a particular

number of times next week.

Remember, the mean number of

times you break down in a week

is 3.4.