Heinrich J.G., Aldinger F. (Eds.) Ceramic Materials and Components for Engines
Подождите немного. Документ загружается.


This Page Intentionally Left Blank

THE ENERGY
AND
THE POWER TIME DEPENDENCE
ON
THE
A WEIBULL STATISTICAL BASED MODEL
ULTRASONIC WELDING PROCESS
-
I.
A.
Bassani",
H.
Kockelmann"",
K.
Kussmaul**
(*)
Laboratbrio Instrumentagio, Materiais e Ensaios (LIME), Regional Integrated University
P.O. Box
44,98800-000
Santo hgelo
Rs,
Brazil
(**)
Staatliche
Materialpruefungsanstalt
(MPA),
University
of
Stuttgart
Pfaffenwaldring
32,70569
Stuttgart, Germany
ABSTRACT
Considering the energy balance of the fiiction con-
ditions of the ultrasonic welding process and based on
measurements of the
growth
rate of the bonded area. a
Weibull statistical four parameter based model is devel-
oped in order to describe the energy and the power time
dependence. The comparison between the developed
model and the experimental results is made by welding
compounds of partially stabilized Zirconia
zIo2
(3%
M,@)
and the heat resistant steel
X5
CrNi
18
10.
using
an interlayer of aluminium alloy AlMgSi
0.5.
INTRODUCTION
In
ultrasonic welding the parts to
be
welded are
clamped together between a sonotrode and an anvil. By
welding metals, glasses and ceramics the sonotrode
vi-
brates parallel to the interface of the two parts and after
a
certain time a joint is formed. The variables involved
are the fiequency of vibration. the vibration amplitude.
the welding time. the clamping force.
as
well
as
the
material properties and the roughness and shape
of
the
parts and of the sonotrode
111.
By welding the deforma-
tion. the welding time or the energy can be controlled.
The formation of a bonded joint between materials sur-
faces has been attributed to (a) the localised melting or
heating arising fiom fiiction. elastic hysteresis and plas-
tic deformation. (b) mechanical interlocking. (c) interfa-
cial nascent bonding and (d) a chemical bond involving
diffusion [2].
The welding process is always accompanied by a
temperature time variation. When joining ceramics and
metals internal stress caused by thermal
expansion
mismatch must be compensated. otherwise fatal damage
due to thermal shock or thermal cycling can occur in the
ceramic. At least a residual stress pattern is induced
which can cause plastic deformation and cracking. af-
fecting the mechanical bond quality [3-51. Together
with phase transformation the result
is
a
final
residual
stress state that can cause the damage of the joint.
Transmission electron microscopy analysis of the
bonded areas of welded parts revealed the formation
of
a fine ,pined structure. resulting fiom both recrystalli-
zation and/or transformation of heavily deformed mate-
rial and short time melting
[a,
7.
For ceramic-metal joints
this
bonded area
has
been as-
sessed to be of the order of a few nanometers [S]. Accord-
ing to the Hall-Perch relation. the mechanical strength can
be expected to be about
2.5
times higher
than
the strength
of the base material. without an embrittling effect [9].
The fact that the bonded area depends on welding time
and all other parameters [l, 8,10,11]. leads to
this
work. If
it is possible to correlate the
growth
of the joined surface
with the energy involved for the generation of the welded
joint. then there is
a
way to simulate with precision the re-
sulting temperature time variation and hence the residual
stress state ofthe surrounding bonded volume.
i
he main purpose of this work is
(1)
to present a model
that describes the energy- and the power-time dependence
based on the ultrasonic welding process energy due to the
fiction conditions.
(2)
to establish a correlation between
the
growth
rate of the welded area and the energy- and
power-time dependence. and
(3)
to compare and validate
the developed model with experimental results.
THEORETICAL PART
Energy and Power Consumption
The enera
E
involved in the bonded surface formation
of
hvo
materials is dependent on an outer fiiction mecha-
nism (sliding between pamers) and on an inner fiiction
mechanism (elasto-plastic and viscoelastic deformation of
the material) [S].
So
E
can be thought
of
as the
sum
of
an
outer
E.F
and an inner energy part
EI.
Considering
two
solid surfaces
A,,
mo&g with respect to another one, both
chemically compatible. for a welding time
t,,
and constant
welding parameters. we assume that the outer energy
E.F
is
proportional to the joined surface
growth
A(t),
and the in-
ner energy
EiF
is proportional to the integral of
A(t)
with
0
I
A(t)
I
A,,.
Relating
E
to
A,,
with the constants
kl
and
k2
leads to:
The factor
k,
represents the input energy per unit sur-
face due to outer fiiction [J/m'] and
k2
the input power per
unit surface due to inner fiction[W/
m'].
For
t
<<
t,,
(A,,
will be joined) the value of
E(t)/A,,
approaches zero. For
t
>>
t,,
(A,,
is joined) the function
E(t)/&
goes toward
a,
333
with
a slope
equal
to
kr.
and
QF/&
assumes the con-
stant value
kl.
The outer
power
time dependence
P.F (t)
is
hence
proportional to the joined surface growth rate
dA/dt.
The inner power time dependence
Pp
is
proportional to
the joined surface growth
A(t).
The total power
P(t)
re-
lated to
&
is:
For
t
<<
t,,
just the outer
power
PeF
influences the
total power
P(t)
and for
t
>>
t,,
it does not influence it.
In
this
case
Pp/&
and
P(t)/&
assume a constant value
equal to
k2.
For
0
I
t
I
t,,
both
E(t)/&
and
P(t)/&
are
dependent on the joined surface growth
A(t).
The con-
cept of time constant
[12].
leads to the weld system time
constant
T~
given by:
(3)
--
kl
-
&OF
L
tW
k2
dP*
Bonded Surface Growth and Bonded Sur-
face Growth Rate
It is presupposed that the probability of surface
as-
pirities touching one another is an absolute continuous
random variable. that obeys a Weibull distribution
[13].
and that the joined surface
A
is
directly proportional to
the weld time
&..
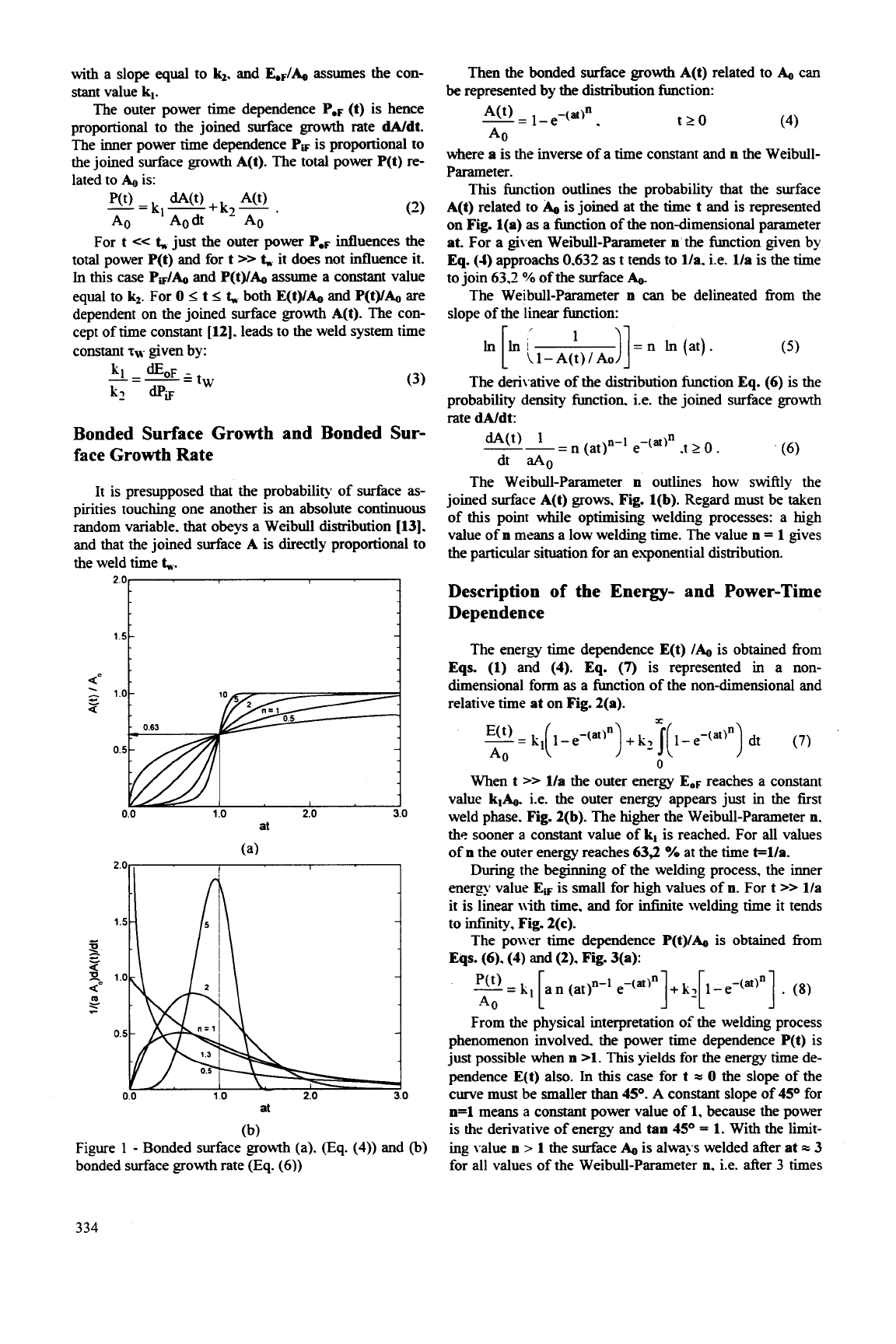
1.5
1
-1
a-
t
.
-
1.0-
7
~
0.63
-
0.0
1
.o
2.0
3.0
at
at
(b)
Figure 1
-
Bonded surface growh (a).
(Eq.
(4))
and
(b)
bonded surface growth rate (Eq.
(6))
Then the bonded surface growth
A(t)
related to
&
can
be
represented
by
the distribution function:
t>O
(4)
-=l-e A(t)
-(at)"
A0
where
a
is
the inverse of a time constant and
n
the Weibull-
Parameter.
This function outlines the probability that the surface
A(t)
related
to
A,,
is joined at the time
t
and is represented
on
Fig.
l(a)
as
a function
of
the non-dimensional parameter
at.
For a given Weibull-Parameter
n
the function given by
Eq.
(4)
approachs
0.632
as
t tends to
l/a.
i.e.
l/a
is
the time
to join
63.2
%
of the surface
&.
The Weibull-Parameter
n
can be delineated fiom the
slope of the linear function:
=
n
h
(at).
(1-
A(t)/
A0
(5)
The derivative
of
the distribution function
Eq. (6)
is the
probability density function. i.e. the joined surface growth
rate
Wdt:
The Weibull-Parameter
n
outlines how swiftly the
joined surface
A(t)
grows.
Fig.
l(b).
Regard must be taken
of
this
point while optimising welding processes: a high
value of
n
means a low welding time. The value
n
=
1
gives
the particular situation for an exponential distribution.
Description
of
the Energy- and Power-Time
Dependence
The energy time dependence
E(t)
/&
is obtained
fiom
Eqs.
(1)
and
(4).
Eq.
(7)
is represented in a non-
dimensional form
as
a function of the non-dimensional and
relative time
at
on
Fig.
2(a).
When
t
>>
l/a
the outer energy
Eo~
reaches a constant
value
kl&
i.e. the outer energy appears just in the first
weld phase.
Fig.
2(b).
The higher the Weibull-Parameter
n.
the sooner a constant value of
kl
is reached. For all values
of
n
the outer energy reaches
632
%
at
the time
t=l/a.
During
the
beL@nhg
of the welding process, the inner
energy value
Ei~
is small for high values of
n.
For
t
>>
l/a
it is linear uith time, and for infinite welding time it tends
to infinity.
Fig.
2(e).
The pouer time dependence
P(t)/&
is
obtained fiom
Eqs. (6).
(4)
and
(2).
Fig.
3(a):
p(t)
-
k,
an (at)"-'
,-(at'"
]
+k2
[
1-e
From the physical inteqretation
of
the welding process
phenomenon involved. the power time dependence
P(t)
is
just possible when
n
>1.
This
yields for the energy time de-
pendence
E(t)
also.
In
this
case for
t
=
0
the slope of the
curve must be
smaller
than
45O.
A
constant slope of
45O
for
n=l
means
a
constant power value of
1.
because the power
is
the
derivative of energy and
tan
45O
=
1.
With the limit-
ing value
n
>
1
the surface
&
is always welded after
at
=
3
for all values of the Weibull-Parameter
n.
i.e. after
3
times
.
(8)
--
-40
[
334
the time constant.
Fig.
1
(a).
1.5
-
4
-
1.0
.
-
-
w’
0.5
0.0
1
.o
2.0
3.0
1.5-
A-
$
.
=
1.0-
-.
-
0.0
1
.o
2.0
3.0
at
-
1.0-
.
-.
-
0.0
1
.o
2.0
3.0
0.0
1
.o
2.0
3.0
at
at
(c)
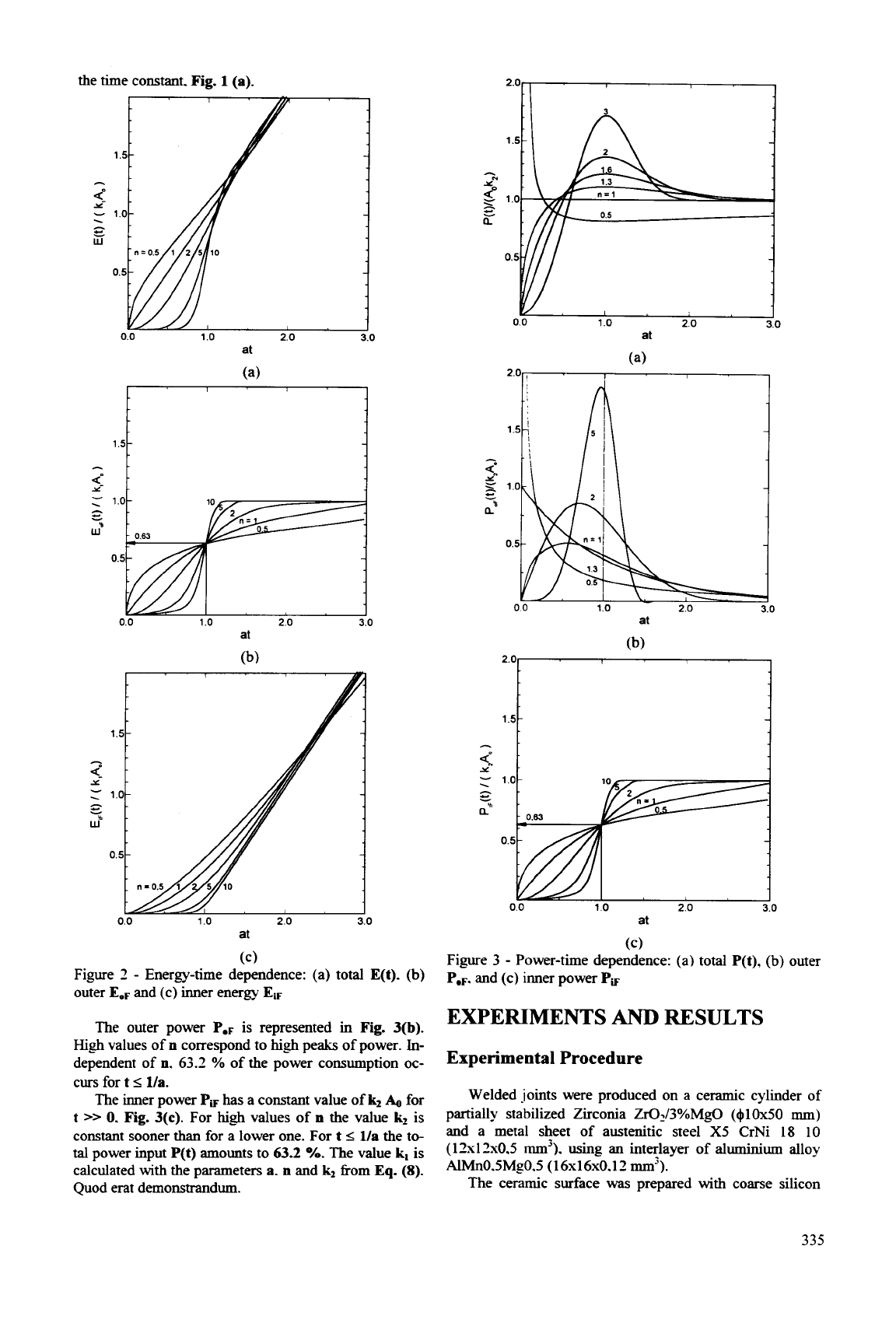
Figure
2
-
Energy-time dependence: (a) total
E(t).
(b)
outer
EeF
and (c) inner energy
E~F
(c)
Figure
3
-
Power-time dependence: (a, total
P(t),
(b)
outer
peF.
and (c)
inner
power
pW
EXPERIMENTS
AND
RESULTS
The outer power
PeF
is
represented
in
Fig.
3(b).
High
values of
n
correspond to
high
peaks of power.
In-
dependent of
n,
63.2
%
of the power consumption oc-
curs for
t
I
l/a.
ne
inner
power
ps
has
a
consmt
value ofk,
A.
for
t
>>
0.
Fig.
3(c).
For
high
values of
n
the value
~i,
is
sooner
than
for
a
lower
one.
F~~
I
1ia
the
to-
power input
p(t)
amounts
to
63.2
%.
The value
k,
is
calculated with the parameters
a.
n
and
kz
kom
Eq.
(8).
Quod erat demonstrandum.
Experimental
h~cedure
Welded
joints
were produced on a ceramic cylinder of
partially stabilized Zirconia
zrO2/3%MgO (410x50
mm)
and a metal sheet of austenitic steel
X5
CrNi
18 10
(1%12~0.5
mm?.
using
an interlayer of
aluminium
alloy
A1Mn0-5Mg0*5
(16s1
6xo.1
=’).
The ceramic surface
was
prepared with coarse silicon
335
carbide grinding paper numbered 500 and
120.
The ce-
ramic sticking out
5
mm
was
firmly fixed on an anvil
and its grooves were rotated
90"
relative to the sono-
trode movement.
Aluminium
and metal steel
were
placed over the ceramic and
all
parts were clamped with
800
N
by the sonotrode.
The sonorrode had
square
pyramidal grooves with
0.5
mm
base length. The fiequency used
was
20
kHz
with an amplitude of
20
pm.
These parameters were
controlled and the power-time acquisition
was
done
with a computational system using a commercial
ultra-
sonic welding machine.
All
welding parameters cited
above were optimised previously to the experiments
[8].
Bonded Surface Growth and Bonded Sur-
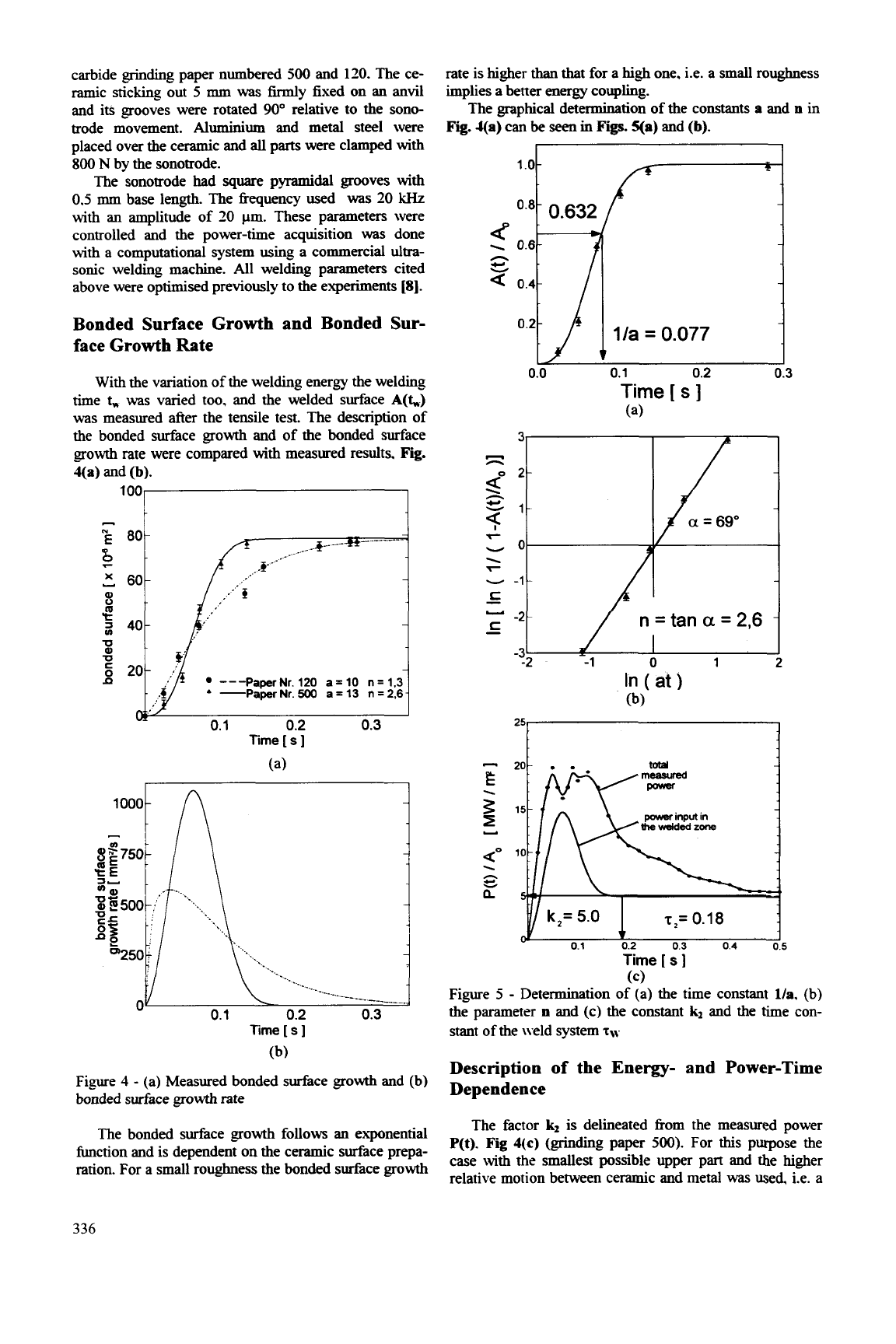
face Growth Rate
With the variation
of
the welding energy the welding
time
t,
was
varied too, and the welded surface
A(t,,)
was
measured after the tensile test. The description of
the bonded surface growth and of the bonded surface
growth
rate were compared with measured results.
Fig.
4(a)
and
(b).
100fiI
t
A -Paper Nr.
500
a
=
13
n
=
2.6
---PaperNr.
120
a=
10
n=
1.3
I
I
0.1
0.2
0.3
Time
[
s]
(a)
-
l0O0t
A
---_
...
___
....
-..
...
0.1
0.2
0.3
0
Time
[
s]
(b)
Figure
4
-
(a) Measured bonded surface growth and (b)
bonded surface growth rate
The bonded surface growth follows an exponential
function and is dependent on the ceramic surface prepa-
ration. For a small roughness the bonded surface growth
rate is higher
than
that for a
high
one, i.e. a small roughness
implies a better
energy
coupling.
The graphical determination
of
the constants
a
and
n
in
Fig.
4(a)
can
be
seen
in
Figs.
Ya)
and
(b).
l/a
=
0.077
0.0
0.1
0.2
0.3
Time
[
s
]
(a)
3
2-
1-
0
-1
-
-
-2
n =tan
a
=
2,6
-
~
-
-2
-1
0
1
2
-3.
In
(
at
)
(b)
25
20-
.
.
total
Time
[
s
i
Figure
5
-
Determination of (a) the time constant
l/a.
(b)
the parameter
n
and (c) the constant
kz
and the time con-
stant of the weld system
TW
Description of the Energy- and Power-Time
Dependence
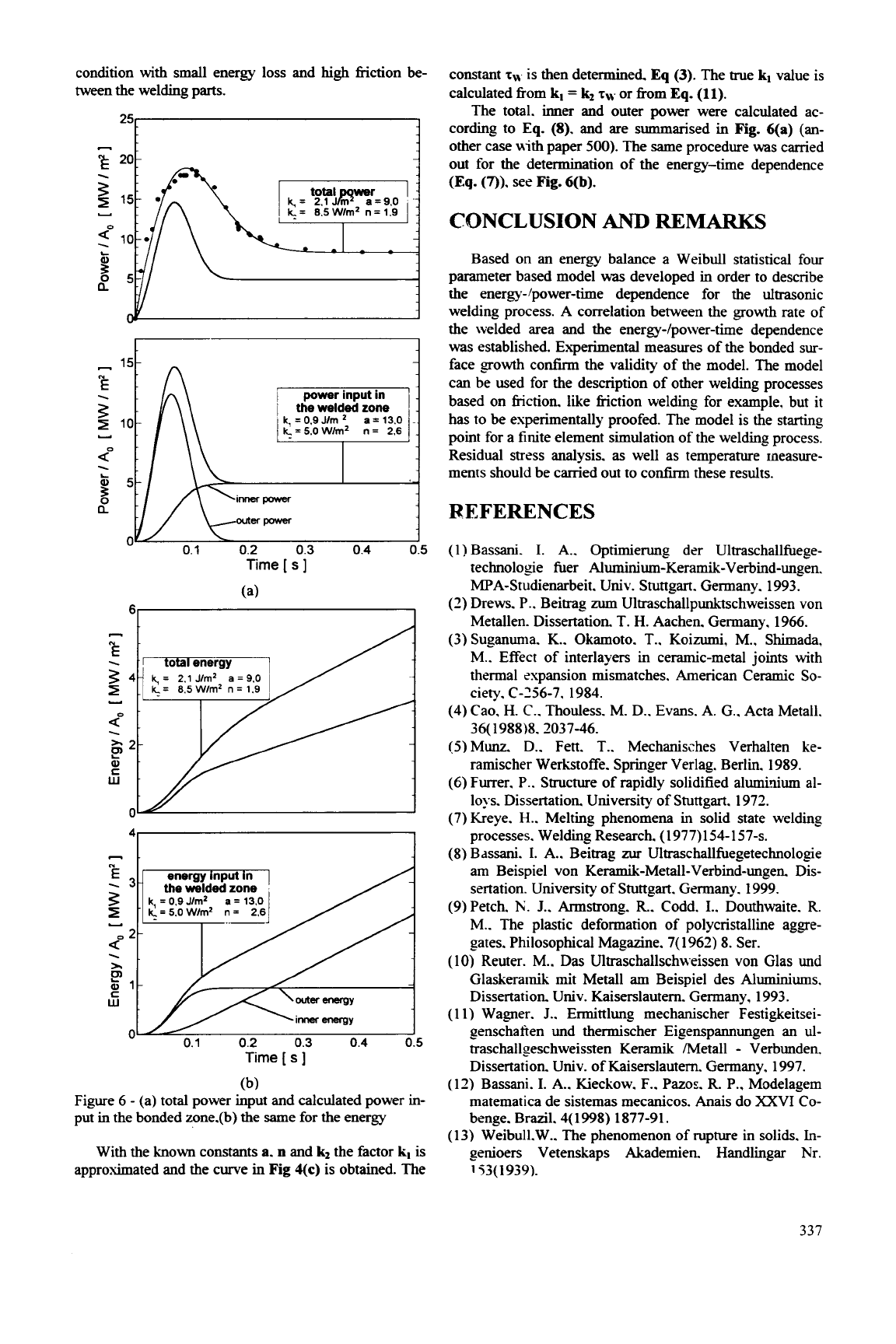
The factor
k2
is delineated fiom the measured power
P(t).
Fig
4(c)
(ginding
paper
500).
For
this
purpose the
case with the smallest possible upper part and the higher
relative motion between ceramic and metal
was
used, i.e. a
336
condition with small energy loss and
high
fiction
be-
tween the welding parts.
20
25!
-
1
power
input
in
j
theweld2edzone
-
k.
=0.9
Jlm
a=
13.0
..
=
5.0
Wlm2 n
=
2.6
-
0.3
0.4
0.5
Time
[
s
]
(a)
7
I
Time
[
s
]
(b)
Figure 6
-
(a) total power input and calculated power
in-
put
in
the bonded zone.(b) the same for the energy
With the
known
constants
a.
n
and
k2
the factor
k,
is
approximated and the curve in
Fig
4(c)
is obtained. The
constant
T,,
is then determined. Eq
(3).
The true
kl
value is
calculated from
k,
=
k2
T~
or fiom Eq.
(11).
The total. her and outer power were calculated ac-
cording to
Eq.
(8).
and are summarised in
Fig.
6(a)
(an-
other case with paper
500).
The same procedure was carried
out for the determination of the energy-time dependence
(Eq.
(7)).
see
Fig.
6(b).
CONCLUSION
AND
REMARKS
Based
on
an energy balance a Weibull statistical four
parameter based model
was developed in order to describe
the energy-/power-time dependence for the ultrasonic
welding process. A correlation between the growth rate
of
the welded area and the energy-/power-time dependence
was established. Eqmimental measures of the bonded
sur-
face growth confirm the validity of the model. The model
can be used for the description of other welding processes
based on fiction. like fiiction welding for example, but it
has
to
be experimentally proofed. The model is the starting
point for a finite element simulation of the welding process.
Residual stress analysis.
as
well as temperature measure-
ments should be carried out to confirm these results.
REFERENCES
(1)Bassani.
I.
A.. Optimierung der Ultraschallfuege-
technologie fuer
Aluminium-Keramik-Verbind-ungen.
MPA-Studienarbeit. Univ.
Stuttgart.
Germany. 1993.
(2)
Drews. P.. Beitrag zum
Ultraschallpunhschweissen
von
Metallen. Dissertation.
T.
H. Aachen. Germany, 1966.
(3)
Suganuma. K.. Okamoto.
T..
Koizumi, M.. Shimada,
M.. Effect of interlayers in ceramic-metal joints with
thermal expansion mismatches. American Ceramic
So-
ciety. C-356-7. 1984.
(4) Cao, H.
C..
Thouless. M. D.. Evans. A. G.. Acta Metall.
36(1988)8.2037-46.
(5)Munz
D..
Fett.
T..
Mechaniszhes Verhalten ke-
ramischer Werkstoffe. Springer Verlag. Berlin. 1989.
(6)
Furrer. P.. Structure of rapidly solidified alumi.lium al-
loys. Dissertation. University of
Stuttgart.
1972.
(7) Kreye.
H..
Melting phenomena
in
solid state welding
processes. Welding Research. (1977)154-157-s.
(8)
Bdssani.
I.
A.. Beitrag
zur
Ultraschallfuegetechnologie
am Beispiel von
Keramik-Metall-Verbind-ungen.
Dis-
sertation. University
of
Sruttgart. Germany. 1999.
(9) Perch.
IG.
J..
Armstrong.
R.
Codd.
I..
Douthwaite. R.
M.. The plastic deformation of polycristalline aggre-
gates. Philosophical Magazine. 7( 1962)
8.
Ser.
(lOY Reuter.
M..
Das Ultraschallschweissen von Glas und
Glaskerainik mit Metall
am
Beispiel des
Aluminiums,
Dissertation. Univ. Kaiserslautern. Germany, 1993.
(1
1)
Wagner.
J..
Ermittlung mechanischer Festigkeitsei-
genschaften und thennischer Eigenspannungen an
ul-
traschallgeschweissten
Keramik
Metall
-
Verbunden,
Dissertation. Univ. of Kaiserslautem. Germany, 1997.
( 12) Bassani.
I.
A.. Kieckow. F.. Pazos. R. P.. Modelagem
matematica de sistemas mecanicos. Anais do XXVI Co-
benge. Brazil.
4(
1998) 1877-91.
(13) Weibu1l.W.. The phenomenon
of
rupture in solids. In-
genioers Vetenskaps Akademien. Handlingar
Nr.
1
53(
1939).
337

This Page Intentionally Left Blank

AN ENGINEER’S APPROACH
TO
DESIGN CERAMIC COMPONENTS
S.
Kruger,
T.
Kentschke*,
H.-J.
Barth
Technical University Clausthal, Institute
For
Tribology and Machine Kinetics,
D-38678
Clausthal-Zellerfeld, Germany
ABSTRACT
By use of the Weibull function it is shown that the
computation of ceramic components can be simplified,
if the Weibull Modulus is high, as is for silicon nitride
or zircon dioxide.
An
approximate solution is derived
for notch effects that uses the notch factor and leads to
a Weibull statistical estimation. Based on these results
an engineer’s strategy for the design of ceramic com-
ponents is proposed.
INTRODUCTION
In
practice a calculation of ceramic components
does
not
take place in most cases. Reasons are the wide
scattering of material strength and life-time and the
missing of a lower strength. These material properties
make a statistical procedure necessary and lead to the
result “the component resists with a certain probabil-
ity”. Even for small loads the probability of failure is
never equal zero, which is unusual for the engineer.
For statistical computation the Weibull function
(1)
is available since the
30s
but is rarely used in practice
without computer software. Various research laborato-
ries world-wide have developed software (e.g.
2,3),
which allows a statistical analysis of a known stress
state. The stress state is determined by a common Fi-
nite Element System (FE). Although these programs
are of great advantage the results can not be better than
the model and material data used. Furthermore FE-
calculations require special knowledge and time.
The result of this situation is that in practice neither
a simple estimation
of
the probability
of
failure nor a
FE-calculation is done when developing ceramic com-
ponents (few exceptions exist).
It is the intention of the authors to demonstrate that
under certain conditions a calculation of ceramic com-
ponents without using a FE-system is feasible and
meaningful.
-
PROCEDURE
The aim of a component computation is to assure
reliable function of the component during a limited
life-time. For metallic materials the component is con-
sidered safe, if the highest equivalent stress of the
component approximates an admissible stress value.
However this can not be applied for ceramics because
of the wide scattering of material strength. The admis-
sible strength is then replaced by the admissible prob-
ability of component failure
Pfli,.
In practice values of
pflim
are
lo4
to
In collaboration with the ceramic industry a list of
requests for a practical computation method was pre-
pared: a)
No
FE-calculations
(-+
“global viewpoint”,
Weibull statistics), b) High reliability of computation
results (“on the safe side”); the material efficiency is of
small importance, c) Use of less and measurable mate-
rial data, d) Consideration of multi-axial stress condi-
tions when necessary, e) Defined scope,
f)
Simple
mathematical procedures.
Below the risk of rupture
Bv
is used instead of the
probability of failure
Pw.
The relationship between
both can be seen from the Weibull function:
Pw
(0)
=
1
-
exp
(-
BY)
where Bv is
for the two-parametrical distribution function. Herein
is:
V
=
component’s volume
Vo
=
characteristic volume
omax
=
maximum stress value
oov
=
characteristic strength
mv
=
Weibull modulus
IN
=
normalised integral
339
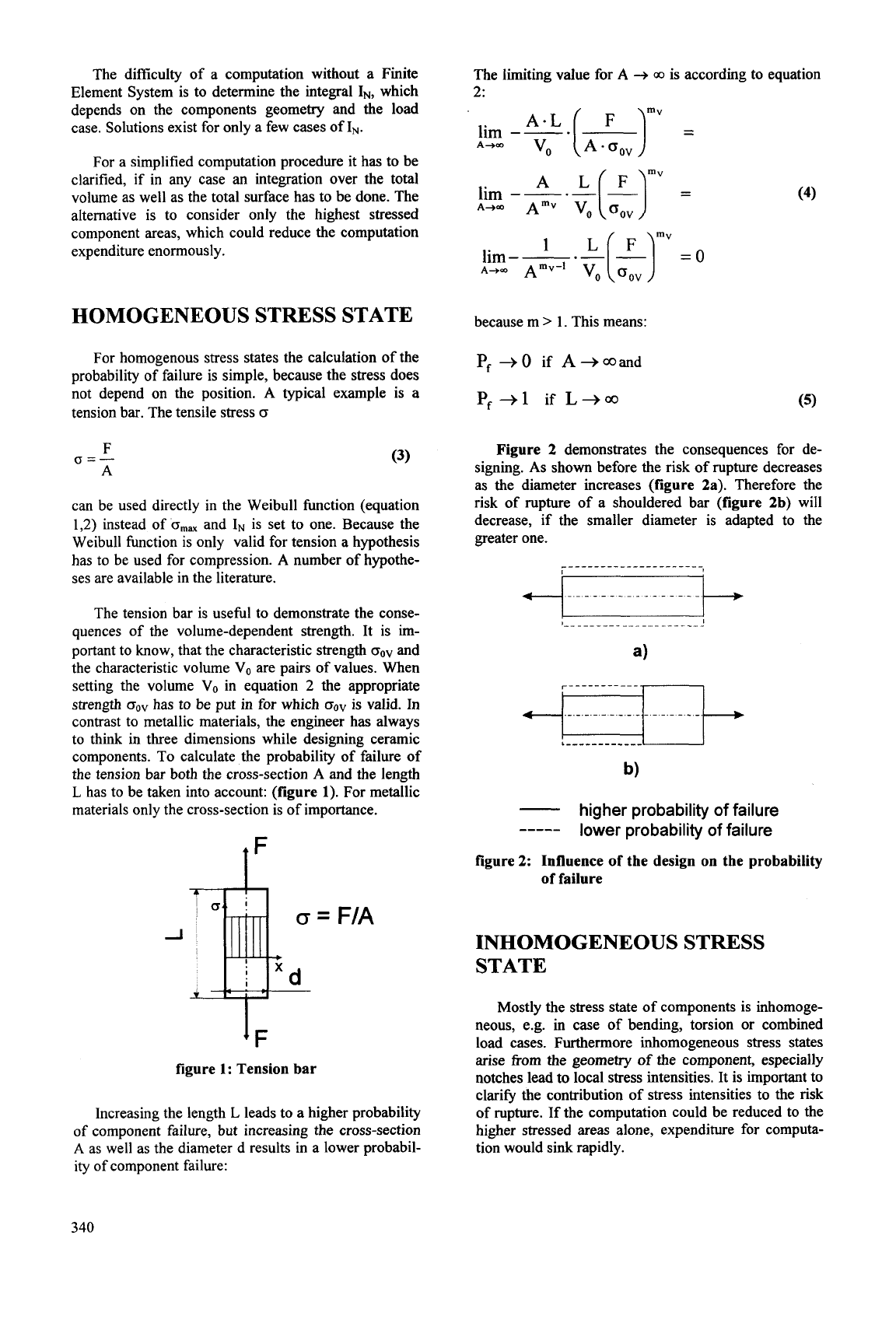
The difficulty of a computation without a Finite
depends on the components geometry and the load
case. Solutions exist for only a few cases of
IN.
The limiting value for
A
-+
00
is according to equation
2:
lim
--.
Element System is to determine the integral
IN,
which
___
"J,"
(
1"
=
A+-
For a simplified computation procedure it has to be
clarified, if in any case an integration over the total
volume as well as the total surface has to be done. The
alternative is to consider only the highest stressed
component areas, which could reduce the computation
"'V
expenditure enormously.
lim--.L(L]
1
=o
vo
oov
A+-
Am,-'
(4)
HOMOGENEOUS
STRESS
STATE
For homogenous stress states the calculation of the
probability of failure is simple, because the stress does
not depend on the position.
A
typical example is a
tension bar. The tensile stress
(J
F
A
(T=-
(3)
can be used directly in the Weibull function (equation
1,2)
instead of
(J,,,~
and
IN
is set to one. Because the
Weibull function is only valid for tension a hypothesis
has to be used for compression.
A
number
of
hypothe-
ses are available in the literature.
The tension bar is useful to demonstrate the conse-
quences of the volume-dependent strength. It is
im-
portant to know, that the characteristic strength
o0v
and
the characteristic volume
Vo
are pairs of values. When
setting the volume
Vo
in equation
2
the appropriate
strength
oov
has to be put in for which
oov
is
valid. In
contrast to metallic materials, the engineer has always
to think in three dimensions while designing ceramic
components. To calculate the probability of failure of
the tension bar both the cross-section
A
and the length
L
has to be taken into account:
(figure
1).
For metallic
materials only the cross-section is of importance.
4F
0
d
because m
>
1.
This means:
P,+O
if A+mand
Figure
2
demonstrates the consequences for de-
signing.
As
shown before the risk of rupture decreases
as the diameter increases
(figure 2a).
Therefore the
risk of rupture of a shouldered bar
(figure 2b)
will
decrease, if the smaller diameter is adapted to the
greater one.
-
higher probability of failure
-----
lower probability of failure
figure
2:
Influence of the design on the probability
of failure
=
FIA
INHOMOGENEOUS
STRESS
STATE
IF
figure
1:
Tension bar
Increasing the length
L
leads to a higher probability
of component failure, but increasing the cross-section
A
as well as the diameter d results in a lower probabil-
ity of component failure:
Mostly the stress state of components is inhomoge-
neous, e.g.
in
case of bending, torsion or combined
load cases. Furthermore inhomogeneous stress states
arise from the geometry of the component, especially
notches lead to local stress intensities. It is important to
clarify the contribution of stress intensities to the risk
of rupture. If the computation could be reduced to the
higher stressed
areas
alone, expenditure for computa-
tion would sink rapidly.
340

The total risk of rupture of two volume elements,
e.g. of a shouldered bar (figure
3),
is according to
equation
2:
of
02/01
and m allow to reduce the computation expen-
diture to the higher stressed component area. However
a criteria has to be found, which helps the engineer to
distinguish between neglectable and not negtectable
areas. This
is
the relative calculation error r:
(9)
Herein for simplification the notch effect is neglected,
which would not be admissible for a real components
computation. Additionally homogeneous load trans-
mission is assumed.
r exists, when the risk of rupture
BI
is
neglected in the
calculations.
A
given maximum value for r (eg
1
%)
leads to the equation
Division of equation
6
by
BG
results in:
(7)
This sum was chosen in
figure
3.
With the assumption
of equal volumes
(V,
=
V2
=
V),
equation
7
gives the
following:
if
V,
=
V2.
Up to now the special case
V,
=
V2
=
V
was dis-
cussed, which rarely arises
in
practice. Therefore the
next step is to investigate the more general case
Vl
#
V2
yet still with the restriction of different and homo-
geneous stress states in the volume elements. Once
again the shouldered bar serves as an example
(figure
3).
Analogous to equations
8.1
and
8.2
is:
BG
I+[$
BG
(1 1.1)
1
--
B,
-
if
A,
>
A2.
(11.2)
1
2=
B
The limiting values for
lim
,
lim
are:
m+O
m+m
lim
:
m+O
BI/BG
=
0,5
;
BJBG
=
0,5
Using r
=
BI/BG
(see equation
9)
it follows
For small values of the Weibull modulus both the
partial risk of rupture
BI
and
B2
contribute substantially
to the total risk of rupture. The theoretical limiting
value of m
=
0
results in equal partial risks of rupture
B,
and
B2
of 50
%
independent from the stress state.
For large values of the Weibull modulus the total risk
of rupture
BG
is determined predominantly by the risk
of
rupture
B2
of
the higher stressed area. The limiting
case m
=
co
corresponds to the deterministic computa-
tion of components
(B2
=
100 YO.)
if r<<
1
and
does not exceed a given value of r. Same examples
have been calculated in
(4).
The contributions of
B1, B2
to the total risk of rup-
ture depend substantially on the proportion of A2/AI as
well as
02/ol
because of the exponential law (see equa-
tions l,
2).
If the proportion of stress
02/o,
is high the
total risk of rupture
BG
is dominated by the risk of
rupture
B2,
even for small values of the Weibull
modulus. The conclusion is that certain combinations
34
1
