Хейденрайх Р. Основы просвечивающей электронной микроскопии
Подождите немного. Документ загружается.


ГЛ.
1.
ИДЕАЛЬНЫЕ,
ИЛИ
ГАУССОВЫ,
ИЗОБРАЖЕНИЯ
определяется
величиной
D
(~).
При
этом,
конечно,
предполагает
СЯ,"что
для
N
атомов
сечение
равно
ND
(~).
Полное
эффективное
сечение
(1.6)
или
(1.4)
есть
руммарная
интенсивность
рассеяния
вне
апертуры,
представленная
на
фиг
5
заштрихованной
пло
щадью.
Даже
если
сечение
N
aTO~OB
приблизительно
равно
ND
(~),
распределение
интенсивности
в
картине
рассеяния
не
всегда
про
порционально
толщине
объекта.
При
малой
эффективной
толщине
pt
падающий
электрон
может
рассеиваться
только
один
раз
-
это
так
называемое
одuо"Краmное
рассеяuие.
При
большей
эффектив
ной
толщине
возможно
двух-'и
трехкратное
рассеяние.
В
случае
же
еще
большей
эффектиi~ной
толщины
результирующая
картина
определяется
,мяого"Краmuым
рассеянием.
Многократное
рассеяние
приводит
к
усложнению
картины
вследствие
изменения
распреде
ления
рассеянной
интенсивности
[3].
При
многократном
рассея
нии
электроны
могут
рассеиваться
в
противоположном
направле
нии
по
отношению
к
падающему
пучку
и
поэтому
не
участвовать
в
формировании
картины
рассеяния
в
апертурной
плоскости.
В
результате
этого
с
увеличением
эффективной
толщины
интен
сивность
рассеяния
уменьшается
медленнее,
чем
можно
было
бы
предполагать.
Установим
критерий,
позволяющий
определить,
до
какой
эффективной
толщины
справедлив
механизм
однократ
ного
рассеяния
[4].
Рассмотрим
образец
толщиной
t.
Пусть
поверхности
образца,
на
которую
падает
пучок
электронов,
соответствует
z =
О.
На
глубине
z
для
слоя
образца
толщиной
dz
интенсивность
рассеяния
вне
апертуры
объектива
dI
= - 1 (z) Q dz,
где
Q -
полное
сече
ние
рассеяния
[см.
(1.6)].
Интегрирование
в
пределах
от
z =
О
до
z = t
дает
хорошо
знакомое
выражение
1 =
/oe-
Qt
•
(1.8)
Необходимо
отметить,
что
Q
имеет
размерность
длины
в
степени
-1,
так
что
Q
есть
число
актов
рассеяния
на
единице
длины
пути.
Тогда
А
=
Q-l
-
средuяя
длuuа
свободuого
пробега
между
двумя
столкновениями.
После
прохождения
образца
толщиной
t =
А
интенсивность
падающего.
пучка
уменьшается
в
е
раз.
Боррис
[5]
определил
критическую
эффективную
толщину
(pt)c
из
требова
ния,
чтобы
произведение
Qt,
входящее
в
(1.8),
равнялосъ
едини
це.
Это
требование
можно
вывести
непосредственно,
если
вероят
ность
рассеяния
описывается
распределением
Пуассона.
Для
объекта
толщиной
t
при
таком
распределении
вероятность
Ь
актов
рассеяния
равна
1 ( t
)Ь
<u
(t) =
Ы
А
e-
t
/
A
•
(1.9)
§
1.
РАССЕЯНИЕ
ЭЛЕКТРОНОВ
43
Если
Ь
положить
равным
единице
(однократное
рассеяние),
то
максимум
вероятности
того,
что
при
про
хождении
толщины
t
будет
только
одно
столкновение,
имеет
место
при
:~/~)
=
e-
t
/
A
[
1-
(
~
) ] =
О,
или
t/A=
Qt
= 1.
Критическая
эффективная
толщина,
таким
обра
.ом,
равна
м
(pt)c = N =
рА.
оО'ат
(1.10)
Если
объект
содержит
более
чем
один
вид
атомов,
то
фор
мула
(1.5)
приобретает
вид
Q
_
~l
N.IТ.
-..:::....J
JVJ'
j
rAe
N J -
число
атомов
сорта
j
в
1
СоМ
3
•
Для
объекта,
состоящего
И8
отдельных
молекул
с
молекулярным
весом
М,
молекулярное
~ективное
сечение
равно
""
Z Q N 00'
мол
О'мол=
kJ
jO'j,
=
М
р,'
j
rДI
')
-
число
аТОМОIJ
сорта
j
с
эффективным
сечением
O'j
на
моле
"11)'.
Есnи
)ICO
О(')ЪОI(Т
представляет
собой
твердый
раствор
пере
.....
01
lCоаЦIНТРnЦИИ
С
)
в/с,м,8
итомоп
сорта
j
с
атомным
ве
...
11,.
'1'0
Q
"--N
"
CJ
~ O.-'J
~M;
OJ.
I
V
••
, ..
BorolCpaTHoro
рассеяния
uриподит
1(
усложнению
коли
'I80T
••••
oro
описания
явления.
Если
же
нас
интересует
только
то,
как.,.
часть
8лектроноп
проходит
через
малую
апертуру
объекти
.а,
то
МО)КНО
показатъ
[1],
что
сечением
однократного
рассеяния
I
(1.8)
можно
пользоваться
даже
для
объектов,
эффективная
тол
щина
которых
превышает
критическую.
ЭКСПОllенциальный
закон
был
проверен
Холлом
[6,
7],
который
DОJlУч.ил
хорошее
соответствие
для
образцов
SiO
толщиной
до
.8000
А.
Работа
была
выполнена
на
микроскопе
RCA
(тип
В)
с
одним
конденсором;
в
..
этом
микроскопе
возможно
периферийное
рас
'сеяние
от
частеи
объекта,
лежащих
за
пределами
апертуры
объек-
тива.
Холл
учитывал
это.
рассеяние
и
многократное
рассеяние,
вводя
в
выражение
(1.8)
параметр
К,
который
дает
часть интен
сивности,
рассеянной
объектом
в
апертуру.
Таким
образом
Холл
8кспериментально
определил
полные
эффективные
сечения
ряда
материалов.
Полученные
им
значения
выражены
в
с.ц2/
г
,
а
не
в
см-l,
как
принято
эдесь,
а
ТОJIщина
объеRта
входит
в
экспоненци
альный
закон
как
эффективная
толщина.
Его
результаты
:тегко
пересчитать,
так
как
введенное
ранее
еечение
Q
равно
просто
Q
=pSc,
где
Sc
(с.м,2/
г
)
-
удеJIьное
сечение,
введенное
Холлом.
В
микроскопе
с
двойным
конденсором
и
пучком
диаметром
от
1
до
2
.м,к
периферийное
рассеяние
будет
значительно
меньше.
и
поэтому
холловский
коэффициент
К
также
уменьшится.
Интен~
сивность
рассеяния
в
апертуру
объектива
будет
рассмотрена
R § 3.
Хотя
ЧИСJlенные
значения
сечений'
рассеяния
будут
рассмот
рены
в
гл.
2,
полезно
представить
себе
порядок
их
величины.
R
таб.тr.
1
приведены
результаты
XOJrJla
с
добавлением
значений
Q.
т
а б
JJ
И
J\
а
:)кепериментаJlьные
аНC:lчения
сечения
рC:lсееяния
при
65 1i&
(согласно
Холлу
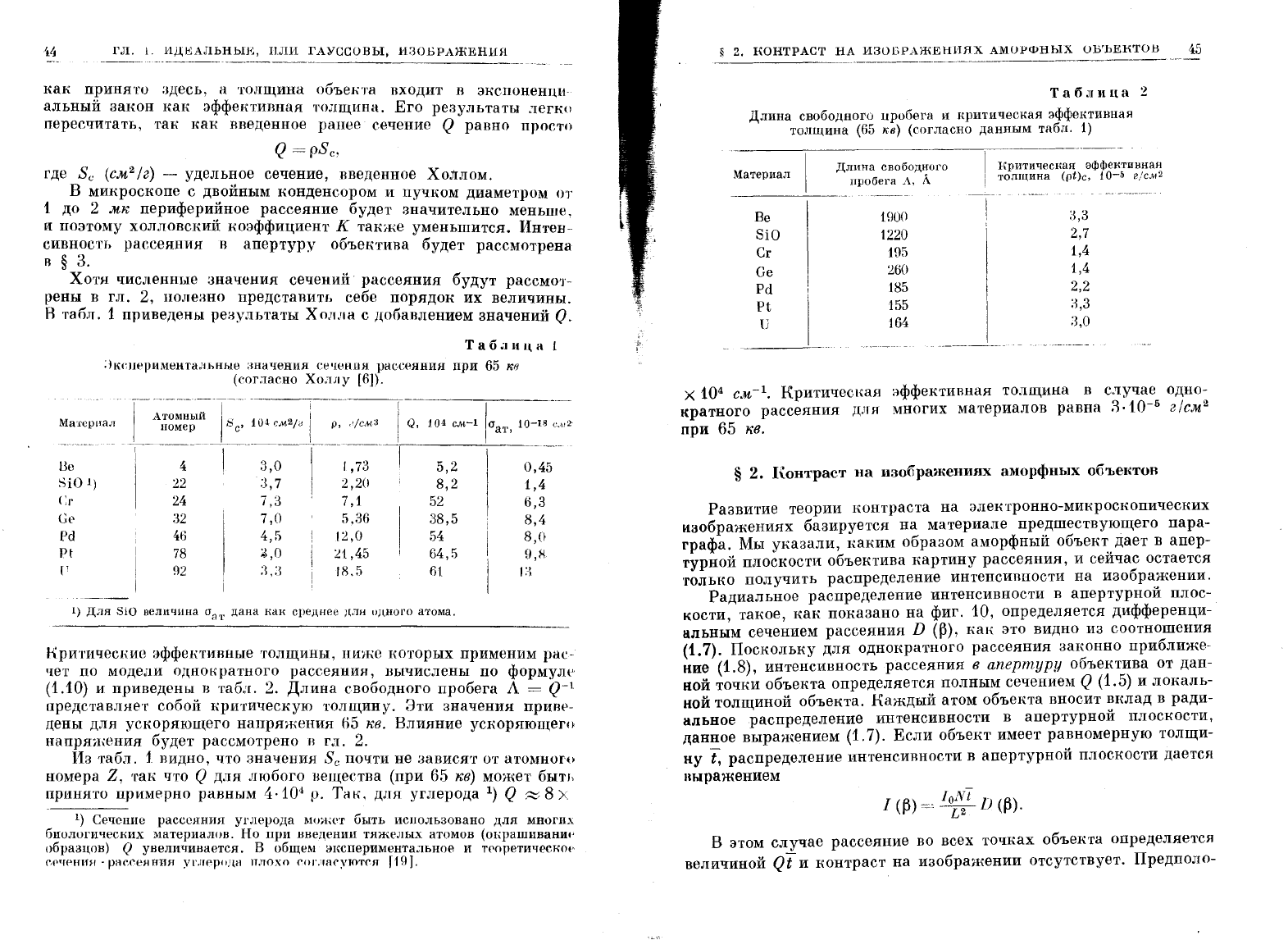
[6]).
lVIa'l'epIlaJТ
Атомный
1.,
I
I . i
номер
I
ь
с'
10'1
cM2/J
I
Р,
";C.M'J
Q,
j 04
",,-1
laaт,
j
0-18
-~''''
.
_-[--_.
__
._---
Ue
I
4
3,0
I
1,73
5,2
0,45
SiO
1)
22 :3,7
2,20
8,2
1,4
Cr
24
7,3
7,1
52
6,3
Ct:'
32
7,0
5,36
38,5
8,4
Pd
46
4,5
12,0
54
8,0-
Pt
78
~3
,О
:И,45
64,5
9,8
(1
~~2
Я,
;З
18,5
61
1')
;)
1)
Для
SiO
величина
аат
дана
нан
среднее
дли
идного
a'l'OMa.
Критические
эффективные
толщины,
ниже
}\оторых
применим
рас
'шт
по
модели
однократного
рассеяния,
вычислены
по
фОрМуЛt
1
'
(1.10)
И
приведены
в
табл.
2.
Длина
евободного
пробега
А =
Q-l
представляет
собой
критическую
толщину.
Эти
значения
приве
дены
для
ускоряющего
напряжения
65
кв.
Влияние
ускоряющего
наПРЯi1~ения
будет
рассмотрено
R
гл.
2.
И3
табл.
1.
видно,
что
значения
Sc
почти
не
зависят
от
атомного
номера
Z,
так что
Q
для
любого
нещеетва
(при
65
кв)
может
БЫТJ)
принято
примерно
равным
4·104
р.
Так,
для
углерода
1)
Q
~
8
><
1)
Сечение
рассеяния
Уl'Jlерода
может
быть
использовано
для
многих
биологических
материалов.
Но
при
вве,rl;ении
тяжелых
атомов
(ОI,раШIIванИI'
образцов)
Q
увеличивается.
В
общем
:шспериментальное
и
т('()ретичеСRОР
е(Нfенин
.
JJНl',ееnпия
УГ.lТАРОЮ-l
П.1Тох()
I'ОI'.:IНl'уютея
r 1
~
J.
§ 2.
НОНТРАСТ
НА
И30ВРАЖЕНИЯХ
АМОРФНЫХ
ОВЪЕНТОН
._------~
-~--~~-----_._--
ТаБJIица
2
Длина
свободного
пробега
и
критическая
эффективная
толщина
(65
.,.в)
(согласно
данным
табд.
1)
Материал
Длина
свободного
I
Нритичесная
эффентиннаи
пробега
Л,
Л
толщина
(pt)c,
10-5
г/см2
--~~~
-
_
..
______
k
______
Ве
1НОО
I
;~,3
I
SiO
1220
I
2,7
Cr
195
I
1,4
Се
260
1,4
I
2,2
Pd
185
Pt
155
:~,3
{]
164
;3,0
45
х
104
с.м,-l.
Критическая
эффективная
толщина
в
случае
одно
кратного
рассеяния
для
многих
материалов
равна
3·10-5
г/см,2
при
65
кв
.
§
2.
Контраст
на
изображениях
аморфных
объектов
Развитие
теории
контраста на
электронно-микроскопических
изображениях
базируется
на
материале
предшествующего
пара
графа.
Мы
указали,
каким
обраЗ0М
аморфный
объект
дает
в
апер
турной
плоскости
объектива
картину
рассеяния,
и
сейчас
остается
только
получить
распределение
интенсивности
на
изображении.
Радиальное
распределение
интенсивности
в
апертурной
плос
кости,
такое,
как
показано
на
фиг.
10,
определяется
дифференци
альным
сечением
рассеяния
D
(~),
кю\
это
видно
И3
соотношения
(1.7).
Поскольку
для
однократного
рассеяния
законно
приближе
ние
(1.8),
интенсивность
рассеяния
в
апертуру
объектива
от
дан
ной
точки
объекта
определяется
полным
сечением
Q (1.5)
и
локаль
ной
толщиной
объекта.
Каждый
атом
объекта
вносит
вклад
в
ради
альноераспределение
интенсивности
в
апертурной
плоскости,
данное
выражением
(1.7).
Если
объект
имеет
равномерную
толщи-
ну
t,
распределение
интенсивности
в
апертурной
плоскости
дается
выражением
в
этом
случае
рассеяние
во
всех
точках
объекта
определяется
величиной
Qt
и
контраст
на
изображении
отсутствует.
Предполо-
4Ь
ГЛ.
1.
ИДЕАЛЬНЫЕ,
или
ГАУССОВЫ,
ИЗОБРАЖЕНИЯ
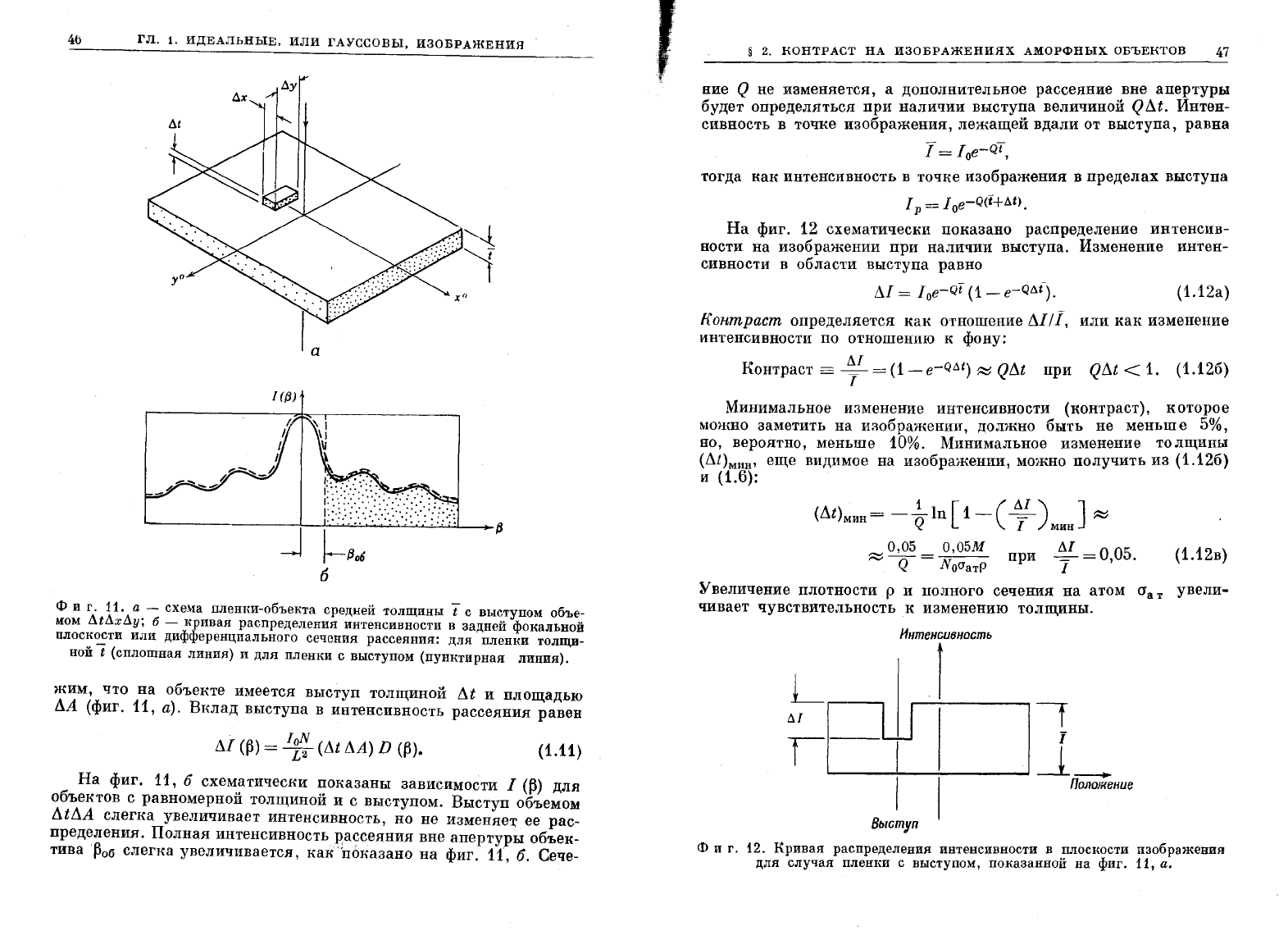
l({3)
j
~~об
6
ф
и
г.
11.
а
-
схема
пленки-объекта
средней
толщины
t
с
выступом
объе
мом
L\tL\xL\y;
б
-
кривая
распределения
интенсивности
в
задней
фокальной
плоскости
или
дифференциального
сечения
рассеяния:
для
пленки
толщи-
ной
t
(сплошная
линия)
и
для
пленки
с
выступом
(пунктирная
линия).
жим,
что
На
объекте
имеется
выступ
толщиной
.1
t
и
площадью
дА
(фиг.
11,
а).
Вклад
выступа
в
интенсивность
рассеяния
равен
.11
(~)
=
It:
(.1t
дА)
D
(~).
(1.11)
На
фиг.
11,
б
схематичеСRИ
показаны
зависимости
1
(~)
для
объектов
с
равномерной
толщиной
и
с
выступом.
Выступ
объемом
.1t.1A
слегка
увеличивает
интенсивность,
но
не
изменяе'J,'
ее
рас
пределения.
Полная
интенсивность
рассеяния
вне
апертуры
объек
тива~об
слегка
увеличивается,
каК"ПОRазано
на
фиг.
11",
б.
Сече-
§ 2.
НОНТРАСТ
НА
ИЗОБРАЖЕНИЯХ
АМОРФНЫХ
ОБЪЕНТОВ
47
ние
Q
не
изменяется,
а
дополнительное
рассеяние
..,вне
апертуры
будет
определяться
при
наличии
выступа
величинои
Q .1t.
Интен
сивность
в
точке
изображения,
лежащей
вдали
от
выступа,
равна
7 =
loe-
Qt
,
тогда
как
интенсивность
в
ТОЧRе
изображения
в
пределах
выступа
/
- 1
e-Q(i+Аt)
р
--
о
•
На
фиг.
12
схематически
показано
распределение
интенсив
ности
на
изображении
при
наличии
выступа.
Изменение
интен
сивности
в
области
выступа
равно
.1/
=
loe-
Qt
(1-е-
QAt
).
(1.12а)
Копт
расm
определяется
как
отношение.11
/1,
или
как
изменение
интенсивности по
отношению
к
фону:
Контраст
=
~
=
(1-е-
QАt
)
~
Q.1t
при
Q.1t < 1.
(1.12б)
1
Минимальное
изменение
интенсивности
(контраст),
которое
можно
заметить на
изображении,
должно
быть
не
меньш
е
5%,
по,
вероятно,
меньше
10%
..
Минимальное
изменение
толщины
(.1t)МJЩ'
еще
видимое
на
изображении,
можно
получить
из
(1.12б)
и
(1.6):
(1.12в)
Увеличение
плотности
р
и
полного
сечения
на
атом
аа
т
увели
чивает
чувствительность
.к
изменению
толщины.
Интенсuвность
r
1]-
Положение
Выступ
Фиг.
12.
Кривая
распределения
интенсивности
в
плоскости
изображения
для
случая
пленки
с
выступом,
показанной
на
фиг.
11,
а.
lL
%0
а
I
~"'~
I I ,
I I
l
I I
A~
I I
х
6
Фиг.
13.
а
-
lIОllеречное
сечение
пленки-объекта
средней
толщины
t
<со
снатом
под
углом
у
к оптичесной
оси;
б
-
кривая
распределения
интен
еивности
в
плоскости
изображения,
показывающая
наличие
контраста,
обусловленного
скатом.
Если
выступ
на
образце
заменить
аморфной
частицей
сече
lIием
Qp
=1=
Q,
то
ROHTpacT
определится
выражением
дI
т
=(1-е-QрL\t)~Qрl1t,
(1.12г)
а
минимальная
толщина
наблюдаемой
частицы
определится
соотно
шением
(1.12в)
с
заменой
Q
на
Qp.
Таким
обраЗ0М,
приближение
простого
однократного
рассеяния
предсказывает,
что
контраст
обусловленный
частицей,
лежащей
на
подложке,
не
зависит
о;
толщины
подложки.
Это
не
всегда
верно
по
двум
причинам.
Во
первых,
многократное
рассеяние
на
толстой
подложке
дает
уве
л
ичение
«электронного
фоню>
даже
на
изображении
частицы.
И,
§ 2.
НОНТРАСТ
НА
ИЗОБРАЖЕНИЯХ
АМОРФНЫХ
ОБЪЕНТОВ
49
во-вторых,
сферическая
аберрация
также
приводит
:к
появлению
фона,
который
может
быть
уменьшен,
но
не
устранен
уменьшени
ем
апертуры
объектива.
Поэтому
все
сказанное
нами
о
контрасте
применимо
лишь
к
объектам
достаточно
тонким
для
того,
чтобы
имело
место
только
однократное
рассеяние.
Как
будет
показано
в
следующей
главе,
имеются
дополнительные
обстоятельства,
спо
собствующие
повышению
контраста
в
краевых
контурах.
При
ИСПОЛЬЗ0вании
реплик
часто
встречается
случай,
показан
ный
на
фиг.
13,
а.
Здесь
представлена
пленка
равномерной
тол-
щины
t
со
«скатом»
под
углом
у
к
нормали
поверхности.
Проекция
толщины
пленки
на
нормаль
равна
t
't'
---,
эфф-
cosy
так
что
I1t
=
1:(_1
__
1)
соэу
и
контраст
равен
~
= ( 1 -
ехр
[ - Qt (
co~
у
-1
) ] ) =
(1.12д)
Изменение
интенсивности
111
на
изображении
«скатю>
пока
зано
на
фиг.
13,6.
Минимальный
обнаружимый
угол
«ската»
может
быть
определен
И3
(1.12д)
и
(1.6):
No(J
Тр
[cos
У]мин
~
ат
N o(JaTtp+O,05M
(1.12е)
В
этом
случае
М
-
молекулярный
вес
и
р
-
плотность.
Таким
обраЗ0М,
рассматриваемый
контраст
на
изображении
возникает
при
значительном
ограничении
падающего
пучка и
сим
метричном
по
отношению
к оптической
оси
расположении
аперту
ры
объектива.
Как
показано
на
фиг.
9,
а,
в
формировании
изобра
жения
участвует
только
центральная
часть
картины
рассеяния.
Но
та
часть
дифракционной
картины,
которая
не
попадает
в
апер
туру,
также
содержит
информацию
об
объекте.
Если
апертура
объектива
сдвинута
относительно
оптической
оси,
изображение
формируется
электронами,
рассеянными
в
сторону
от
центра
объек
та.
Полученное
таким
обраЗ0М
изображение
называется
mемно
nОЛЪJtЫМ.
Но
смещение апертуры
-
не
наилучший
способ
полу
чения
темнопольного
изображения,
так
как
в
этом
случае
исполь
зуются
непараксиальные
пучки
и,
следовательно,
увеличиваются
сферическая
аберрация
и
астигматизм.
Предпочтительнее
накло
нять
осветительную
систему
микроскопа,
так
чтобы
падающий
4
Р.
Хейденрайх
50
ГЛ.
1.
ИДЕАЛЬНЫЕ,
или
ГАУССОВЫ,
ИЗОБРАЖЕНИЯ
пучок
не
попадал
В
апертуру
объектива.
Вследствие
этого
рассеян
ные
лучи,
попадающие
в
апертуру,
будут
более
симметричными
относительно
оптической
оси
объектива.
На
фиг.
14
показ3.но
положение
системы
объектива
при
получении
темнопольного
изо
бражения.
Положение
апертуры
показано
на
фиг.
10.
В
случае
темнопольного
изображения
задача
обратная
-
най
ти
рассеяние
в
апертуру,
а
не вне
апертуры
объектива.
Эта
задача
может
быть
решена
следующим
образом.
Предположим,
что
интенсивность
рассеяния
примерно
постоян-
на
по
диаметру
апертуры
и
определяется
средним
значением
D
(~o),
где
~o
-
угол
наклона
падающего
пучка.
Телесный
угол,
опираю
щийся
на
апертуру
объектива,
равен
Q
л
(rап)2
А2
ап
~
L2 =
Л",об,
где
7'ап
-
радиус
отверстия,
а
L -
расстояние
от
объекта
до
апер
тур
ной
диафрагмы.
Часть
электронов,
рассеянных
в
апертуру
атомом
объекта,
согласно
(1.3а),
равна
~n
--
1
~
лD
(~o)
~~б.
(1.13а)
На
глубине
объекта
z
интенсивность
потока
электронов,
падающих
на
атом,
равна
10
ехр
( - Qz),.
так
что
часть
электро
нов,
рассеивающихся
в
апертуру
атомом,
лежащим
на глу
бине
z,
равна
(1.13б)
Как
И
раньше,
примем
что
еечение
рассеяния
аддитивно,
так
что
для
N dz
атомов,
лежащих
в
слое
между
z
и
z+
dz,
интен
сивность
рассеяния
в
апертуру
dI
=
дnN
dz.
Тогда
интенсивность
раесеяния
при
толщине
образца
t
равна
t
1 =
лlоND
(~o)
~~б
~
eQzdz =
о
=лlоN(
D~o)
)
~~б(еQt-1)=лlо
(D(j~~o)
)~~б(еQt-1),
(1.14)
где
Q=Na
aT
•
Контраст
на
темнопольном
изображении
частицы
с
полным
~ечением
Qp
и
толщиной
бt,
лежащей
на
подложке
толщиной
t.;и
сечением
Q,
найдем
из
выражения
(1.14):
~I
1
Фиг.
14.
Формирование
темнопольного
изображения
при
наклоне
освети-
теля
на
угол
/30
к
оптической
оси
оБЪ(штивной
линзы
(ер.
с
фиг.
9,
а).
I
На
фиг.
10
поиазана
часть
распределения
интенсивности,
-Дающая
темнопольное.'
изображение.

52
ГЛ.
1.
ИДЕАЛЬНЫЕ ИЛИ
ГАУССОВЫ,
ИЗОБРАЖЕНИЯ
При
Q/3t
и
Qt,
много
меньших
единицы,
выражение
упро
щается:
(1.15)
_~ecь
N
р
и
N -
число
атомов
на
1
с,м,3
частицы
и
подложки,
Dр(~о)--среднее
дифференциальное
сечение
над
апертурой
и
D
(~o)
-
среднее
дифференциальное
сечение
подложки.
Предпо
лагая
/)./
//
:=:::::
0,05,
получаем
минима.льную
толщину
частицы,
еще
видимую
в
темном
поле:
(1.16а)
Для
сравнения
приведем
соответствующее
выражение
для
случая
светлого
поля:
(1.16б)
Численные
значения
дифференциальных
сечений,
которые
необходимы
для
оценки
6t
мин
из
сОотношения
(1.16а),
будут
рас
смотрены
в
гл.
2
1).
§ 3.
Расселние
на
Rвазиаморфных
телах
Даже
В
том
случае,
когда
атомы,
из
которых
состоит
тело,
расположены
хаотически,
без
периодичности
в
обычном
смысле
этого
слова,
некоторые
межа
томные
расстояния
встречаются
чаще
чем
другие.
Если
некоторый
атом
в
теле
выбран
за
начальный'
то
рас~ределение
ближайших
к
нему
~оседних
а
томов,
следующи~
ближаиших
соседних
а
томов
и
так
далее
можно
описать
функцией
радиального
распределения.
Рассмотрим
сферическую
оболочку
радиусом
r
и
толщиной
dr
с
центром,
совпадающим
с
выбранным
атомом.
Предположим,
что
все
атомы,
составляющие
тело
одина
ковы.
Объем
сферической
оболочки
равен
4лг
2
dr,
так
ч;о,
если
локальную
ПЛОтность
атомов
обозначить
Р
(r),
число
атомов
в
обо
лочке
будет
равно
dN
=
4nr
2
p (r)
dr.
(1.17)
Изменение
4лг
2
р
(г)
обычно
представляют
графически
в
зави
симОсти
от
r.
Задача
состоит
в
том,
чтобы
получить
функцию
ради
ального распределения
4лг
2
р
(г)
из
экспериментальных
данных
по
рассеянию
объектом
рентгеновских
лучей
или
электронов.
1)
Для
углеродноЙ
пленки
тОлщиной
100
А
минимальное
различимое
утолщение
в
светлом
поле
равно
70
А,
в
темном
поле
- 5
А
[подсчитано
по
(1.16а)
и
(1.16б)
для
ускоряющего
напряжения
100
1\:8].
§ 3.
РАССЕЯНИЕ
НА
:КВАЗИАМОРФНЫХ
ТЕЛАХ
53
Основой
для
анализа
картины
рассеяния
рентгеновских
лучей
на
некристаллических
телах
явилась
опубликованная
в
1915
г.
работа
Дебая
[8].
Дальнейшее
развитие теория
получила
в
работе
Цернике
и
Принса
[9].
При
расчете
картины
рассеяния,
произво
димого
аморфным
телом
или
жидкостью,
необходимо
принять
в
расчет
волновые
свойства
излучения,
так
как
отдельные
волны,
рассеянные
атомами,
могут
интерферировать.
Введем
а~плитуду
рассеяния
электрона
f (s); f
(s)
--
амплитуда
электроннои
волны,
рассеянной
изолированным
атомом,
отнесенная
к
падающей
волне
единичной
амплитуды.
Амплитуда
рассеяния
f (s),
как
будет
видно
из
последующего,
просто
связана
с
дифференциальным
сечением.
Величина
s
назы
вается
nара.Jrtеmро.л-t
рассеяния
и
определяется
равенством
4л
.
~
s=:=:
T
S1n
т.
(1.18)
Параметр
рассеяния
применяется
во
всех
расчетах,
связан
ных
с
рассеянием;
л
-
длина
волны
и
~
--
угол
рассеяния.
Обозначение
8,
часто
употребляемое
в
(1.18)
вместо
~/2,
мы
сохра
ним
для
угла
Брэгга
.при
дифракции
на
кристаллах.
Используя
радиальное
распределение
(1.17),
можно
пока
зать,
что
в
случае
кристаллического
объекта
интенсивность
рассеяния
[101
как
функция
параметра
рассеяния
s
может
быть
выражена
соотношением
1(8)
=N'lf(s)12
[1+4л:
\ r2p(r)
sin8r
dr],
10 J
8,
(1.19а)
где
N'
--
число
атомов
кристалла.
Интегрирование
ведется
по
всему
кристаллу.
При
выводе
этого
выражения
предполагалось,
что
кристалл
состоит
из
одинаковых
атомов.
В
том
случае,
когда
кристалл
состоит
из
разнородных
атомов,
выражение
для
интен
сивности
рассеяния
становится
более
сложным
[101.
Интеграл
в
выражении
(1.19а)
может
быть
представлен
в
виде
r
с
\ ) s
in
8r
4
\"
sin
8r
4л
J r
2
p
(r
-8r-
dr =
л
J r
2
[р
(г)
--
Ро]
-8r-
dr
+
о
r
с
~
sin
8r
+
4л
г
2
ро
--
dr,
8r
О
(1.19б)
где
Ро--
среднее
число
атомов
на
единицу
объема
и
гс
-
радиус
кристаллита
в
объекте.
54
ГЛ.
{.
ИДЕАЛЬНЫЕ,
ИЛИ
ГАУССОВЫ,
ИЗОБРАЖЕНИЯ
На
расстоянии
L
от
образца
толщиной
t
интенсивность
рас
сеяния
на
единице
площади
объекта
определяется как
II~)
=
~:
\ f
(s)
12
(1
+8
р
+
80)'
(1.19в)
тде
8
р
и
80
равны
r
с
~
sin
sr
8
р
_
4л
r
2
[р
(r)-po]
--
dr,
sr
о
r
с
80 =
4..,.
\ r
2
sinsr
dr
."
J
Po---;r
о
и
N -
число
атомов
в
еДfинице
объема
объекта.
Если
кристал
литы
большие,
так что
[р
(r) -
Ро]
стремится к
нулю,
когда
r
приближается
к
rc,
ситуация
становится
похожей
на
случай
рассеяния
жидкостью;
при
этом
верхний
предел
8
р
может
быть
бесконечным.
Если
кристаллит
не
настолько
велик,
чтобы
[р
(r) -
Ро]
стремилось
к
нулю,
Sp
будет
зависеть
от
размера
кристалла.
Выражение
(1.19в)
может
быть
ИСПОЛЬЗ0вано
при
расчете
интен
сивности
рассеяния
различными
материалами,
аморфными
или
кристаллическими.
Функция
радиального
распределения
может
быть получена
И3
.
наблюдаемой
картины
рассеяния
с
помощью
интегрального
преобразования
Фурье
[11-'13].
Она
дает
ценную
информацию
о
ближайшем
окружении
данного
атома.
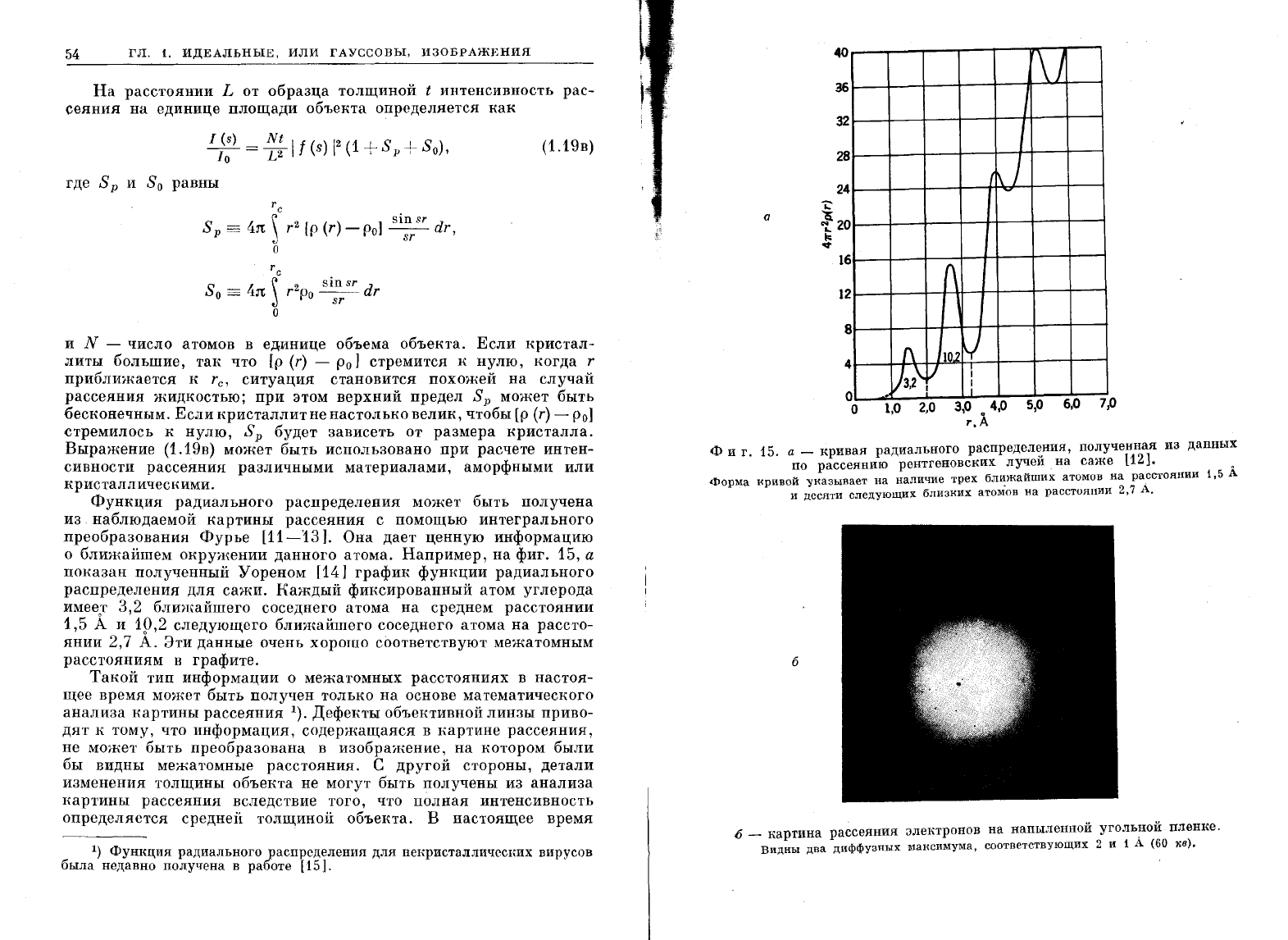
Например,
на
фиг.
15,
а
показан
полученный
Уореном
[14]
график
функции
радиального
распределения
для
сажи.
Каждый
фин:сированный
атом
углерода
имее;г
3,2
ближайшего
соседнего
атома
на
среднем
расстоянии
1,5
А
и
19,2
следующего
ближайшего
соседнего
атома
на
рассто
янии
2,7
А.
Эти данные
очень
хорошо
соответствуют
межатомным
расстояниям
в
графите.
Такой
тип
информации
о
межатомных
расстояниях
в
настоя
щее
время
может
быть
получен
только
на
основе
математического
анализа
картины
рассеяния
1).
Дефекты
объективной
линзы
приво
дят
К
тому,
что
информация,
содержащаяся
в
картине
рассеяния,
не
может
быть
преобразована
в
изображение,
на
котором
были
бы
видны
межатомные
расстояния.
С
другой
стороны,
детали
изменения
толщины
объек
та
не
могут
быть
получены
И3
анализа
картины
рассеяния
вследствие
того,
что
полная
интенсивность
определяется
средней
толщиной
объекта.
В
настоящее
время
1)
ФУНIЩИЯ
радиального
распределения
для
неI{ристаллических
вирусов
была
недавно
получена
в
работе
[15].
а
40
Э6
32
28
24
'i:'
~20
t;
'Iit
16
12
8
4
о
о
\)
J
I
~
J
-
{\
,
f\
JI01
~
~з,~~
.
1,0
2,0
I
:
3,0
4,0
r,A
5,0
6,0
7,0
ф
и
г.
15.
а
_
кривая
радиального
распредел~ния,
полученная
И3
данных
по
рассеянию
рентгеновских
лучеи.
на
саже
[12].
Форма
нривой
уназывает
на
наличие
трех
ближайших
атомов
на
расстоянИИ
1,5
А
И
десяти
следующиХ
близних
атом'ов
на
расстоянии
2,7
А.
6
6 -
картина
рассеяния
элеI{ТРОНОВ
на
напыленной
уголь;ной.
пленке.
Видны
два
диффузных
мансимума,
соответствующих
2
и
1
А
(60
nв).

56
ГЛ.
1.
ИДЕАЛЬНЫЕ,
ИЛИ
ГАУССОВЫ,
ИЗОБРАЖЕНИЯ
распределение
интенсивности
рассеяния
используется
только
для
определения
эффективного
сечения
рассеяния
вне
апертуры
объектива
(для
анализа
контраста,
связанного
с
ТОЛIЦиной
объ
екта).
Мы
можем
получить
некоторую
полезную
информацию
из
соот
ношения
(1.19а)
даже
без
детального
анализа.
Рассмотрим
только
одно
межатомное
расстояние
r1,
как,
например,
межатомное
рас
стояние
в
молекуле
хлора.
В
этом
случае
интенсивность
рас
сеяния
равна
[1 (s)]r =
NL~1
t I f
(8)
12
(1
+
sin
sr1 ) •
1 sr1
(1.20а)
Легко
видеть,
что
она
принимает
экстремальные
значения
при
tg
8r1 = sr1;
первый
максимум
наблюдается
при
sr1 =
2,46л
(см.
приложение
1,
табл.
14)
или
в
соответствии
с
(1.18)
при
условии
л
= (0,814)
2r1
sin
~:I1~ИС
,
(1.20б)
которое
очень
напоминает
закон
Брэгга:
л
=
2а
sin
е.
ВооБIЦе
для
всех
твердых
тел
максимум
выражения
(1.19а)
удовлетворяет
условию
Брэгга
или
очень
близкомук
нему
условию.
На
фиг.
15,
б
представлена
картина
рассеяния,
полученная
от
напыленной
пленки
углерода.
Видны
два
максимума
интенсивнрсти,
первый
соС}тветствует
расстоянию,
равному
примерно
2
А,
второй-
1
А,
что
близко
к
брэгговским
расстояниям
{100}
графита.
Изу
чение
картины
дифракции
электронов
на
саже
[16]
показало,
что
гексагональные
слои
углерода
имеют
ожидаемые
расстояния
1);
отраженные
волны
находятся
в
фазе
только
для
расстояний,
пре
вышаюIЦИХ
расстояния
между
базисными
плоскостями
в
9-4
ра
за,
что
дает
эффективный
размер
кристалла
порядка
12
А.
Из
соотношения
(1.20б)
можно
получить
важный'
результат,
если
принять,
что
угол
~маис
мал.
Тогда,
пренебрегая
числен
ным
коэффициентом
0,814,
получаем
(1.21а)
При
расстоянии
L
от
объекта
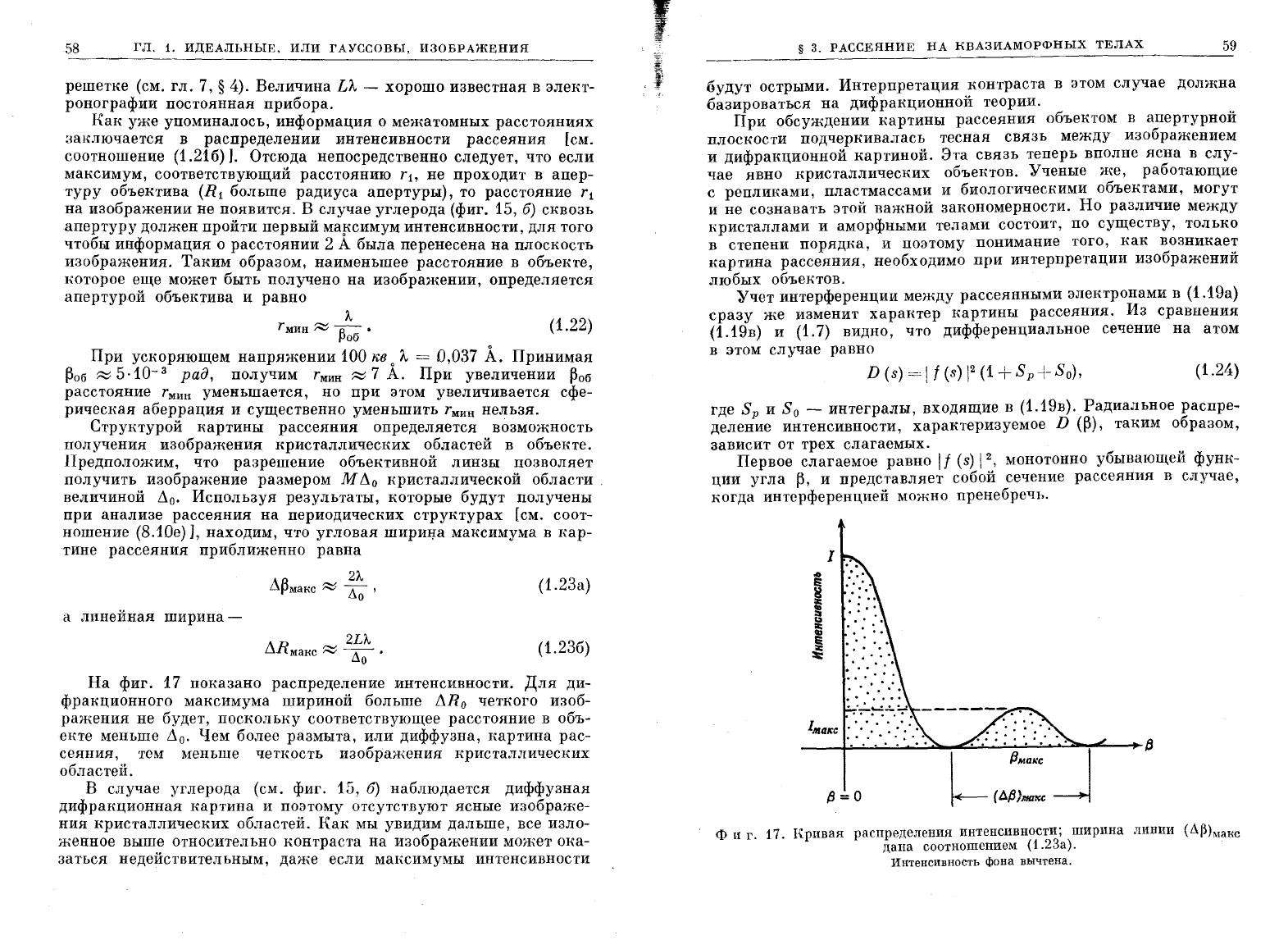
максимум
будет
при
R
t
=
L~маис
(геометрия
показана на
фиг.
16),
так
что
(1.216)
Отсюда
видно, что
расстояния
в
картине
рассеяния
обраml-lЬ~
расстояниям
в
объекте
и,
следовательно,
обратны
расстояниям
1)
3,37
А
-
расстояние
между
базисными
плосн:остями.
§
3.
РАССЕЯНИЕ
НА
RВАЗИАМОРФНЫХ
ТЕЛАХ
57
Ф
.
16
Схема
поясняющая
геометричесн:ие
соотношения
между
УГЛОI\I
и
Г.·
,
й
адиусом
н:ольца
R
t
рассеяния
для
МaI{симума
интеНСИБНОСТ~
t-'маис
II
р
на
дифрющионнои
I{артине.
Расстолние
в
объеите
Тl
связано
с
расстоянием
R 1
на
дифраиционной
иартине
соотНо
шением
Тl
=
L'л/R
1
•
на
изображении
1).
Наличие
такой
связи
между
объ~ктом
и
карти:
ной
рассеяния
привело
к
развитию
представлении
об
обратнои
1)
Распределение
амплитудЫ
рассеяния
в
задней
фон:альной
ПЛОСН:ОСТИ
фактически
соответствует
сечению
обратноii
решеТlШ
объеlпа.
58
ГЛ.
1.
ИДЕАЛЬНЫЕ,
ИЛИ
ГАУССОВЫ,
ИЗОБРАЖЕНИЯ
решетн.е
(см.
гл.
7, § 4).
Величина
Lл
-
хорошо
известная
В
элект
ронографии
постоянная
прибора.
Как
уже
упоминалось,
информация
о
межатомных
расстояниях
заключается
В
распределении
интенсивности
рассеяния
[см.
соотношение
(1.21б)].
Отсюда
непосредственно
следует,
что
если
максимум,
соответствующий
расстоянию
rl,
не
проходит
в
апер
туру
объектива
(R
1
больше
радиуса
апертуры),
то
расстояние
r1
на
изображении
не
появится.
В
случае
углерода
(фиг.
15,
б)
сквозь
апертуру
должен
пройти
первый
ма!\симум
интенсивности,
для
того
чтобы
информация
о
расстоянии
2
А
была
перенесена
на
плоскость
изображения.
Таким
образом,
наименьшее
расстояние
В
объекте,
которое
еще
может
быть
получено
на
изображении,
определяется
апертурой
объектива
и
равно
'А
rмин
~
-А-'
(1.22)
",об
При
ускоряющем
напряжении
100
кв
о
л
= 0,037
А.
Принимая
ВОб
~
5·
10-
3
рад,
получим
r
мин
~
7
А.
При
увеличении
ВОб
расстояние
rмин
уменьшается,
но
при
этом
увеличивается
сфе
рическая
аберрация
и
существенно
уменьшить
rмин
нельзя.
Структурой
картины
рассеяния
определяется
возможность
получения
изображения
кристаллических
областей
в
объекте.
Предположим,
что
разрешение
объективной
линзы
позволяет
получить
изображение
размером
М
~o
кристаллической
области.
величиной
~o.
Используя
результаты,
которые
будут
получены
при
анализе
рассеяния
на
периодических структурах
[см.
соот
ношение
(8.10е)],
находим,
что
угловая
ширица
максимума
в
кар
тине
рассеяния
приближенно
равна
а
линейная
ширина-
2L'A
~RMaHc~~.
(1.23а)
(1.23б)
На
фиг.
17
показано
распределение
интенсивности.
Для
ди
фракционного
максимума
шириной
больше
~R
о
четкого
изоб
ражения
не
будет,
поскольку
соответствующее
расстояние
в
объ
екте
меньше
до.
Чем
более
размыта,
или
диффузна,
картина
рас
сеяния,
тем
меньше
четкость
изображения
:кристалличес:ких
областей.
В
случае
углерода
(см.
фиг.
15,
б)
наблюдается
диффузная
дифракционная
картина
и
поэтому
отсутствуют
ясные
изображе
ния
кристаллических
областей.
Как
мы
увидим
дальше,
все
изло
женное
выше
относительно
контраста
на
изображении
может
ока
заться
недействительным,
даже
если
МaI\СИМУМЫ
интенсивности
§
3.
РАССЕЯНИЕ
НА
НВАЗИАМОРФНЫХ
ТЕЛАХ
59
будут
острыми.
Интерпретация
контраста
в
этом
случае
должна
базироваться
на
дифракционной
теории.
При
обсуждении
картины
рассеяния
объектом
в
апертурной
плоскости
подчеркивалась
тесная
связь
между
изображением
и
дифракционной
картиной.
Эта
связь
теперь
вполне
ясна
В
слу
чае
явно
кристаллических
объектов.
Ученые
же,
работающие
с
репликами,
пластмассами
и
биологическими
объектами,
могут
и
не
сознавать
этой
важной
закономерности.
Но
различие
между
кристаллами
и
аморфными
телами
состоит,
по
существу,
только
в
степени
порядка,
и поэтому
понимание
того,
как
возникает
картина
рассеяния,
необходимо
при
интерпретации
изображений
любых
объектов.
Учет
интерференции
между
рассеянными
электронами
в
(1.19а)
сразу
же
изменит
характер
картины
рассеяния.
Из
сравнения
(1.19в)
и
(1.7)
видно,
что
дифференциальное
сечение
на атом
В
этом
случае
равно
D(s)=lf(s)1
2
(1+S
p
+S
o
),
(1.24)
где
Sp
и
So
-
интегралы,
входящие
в
(1.19в).
Радиальное
распре~
деление
интенсивности,
характеризуемое
D
(В),
таким
образом,
зависит
от
трех
слагаемых.
Первое
слагаемое
равно
I f
(s)
12,
монотонно
убывающей
функ
ции
угла
В,
и
представляет
собой
сечение
рассеяния
в
случае,
:когда
интерференцией
м()жно пренебречь.
ф
и
г.
17.
Н.РlIвая
распределения
интенсивнОСТИ;
ширина
линии
(д.~)MaHC
дана
соотношением
(1.23а).
Интенсивность
фона
вычтена.

60
ГЛ.
1.
ИДЕАЛЬНЫЕ,
ИЛИ
ГАУССОВЫ,
ИЗОБРАЖЕНИЯ
Второе
сечение
I f
('8)
I 2S
p
приводит
К
появлению
В
картине
рассеяния
максимумов
И минимумов.
На
фиг.
18,
а
показана
картина
рассеяния
на
германиевой
пленке,
полученной
осажде
нием
из
пара
при
температуре
подложки
750
с.
В
случае
пленки,
полученной
при
температуре
4000
С
(фиг.
18,
б),
размытые
кольца
переходят
в
острые
максимумы
(111)
И
(311),
что
указывает
на
ярко
выраженную
кристал
личность.
ф
11
г.
18.
Дифрак
ционная
картина
для
германия,
снятая
на
просвет
при
45
кв.
а
-
германий
конден
сировался
на
подложку,
нагретую
на
750
С
(диф
фузные
маисимумы);
б
-
то
же,
что
и
на
фиг.
а,
но
темпсратура
подложии
4000
С.
Пер
вые
два
гало
фиг.
а
пре
вратились
в
кольца,
со
ответствующие
(111),
(220)
и
(311).
Третье
дифференциальное
сечение
в
(1.24)
равно
I f
(s)
I 2S
0
•
Так
как
So
ограничено
радиусом
кристаллита,
оно
равно
нулю
только
тогда,
когда
Т
с
=
О,
т.
е.
в
случа~
жидкости.
При
размерах
кристалллов
до
10
А
интенсивность
рассеяния,
связанная
с
этим
сечением,
падает
до
нуля
в
пределах
апер
туры.
Интенсивность
рассеяния,
связанная
с
S
о,
соответствует
спектру
нулевого
порядка.
и
поэтому
она
не дает
вклада
В
рассеяние
вне
апертуры.
Полное
сечение
для
рассеяния
вне
апер
туры
может
быть получено
И3
СОотноше
ний
(1.24)
и
(1.4).
Интеграл
S
р
не
равен
нулю
во
всем
интервале
углов,
но
ИМ
можно
пренебречь
в
области углов
от
~Об
до
n.
Сечение
S
о
приблизительно
равно
нулю
вне
апертуры.
Таким
обраЗ0М,
полное
сечение
на атом
будет
равно
n
а
ат
=
2л
~
I f
(s)
12
sin
~ d~.
f3
0
б
(1.25)
Это
выражение
-
отправная
точка
для
вычисления
полного
сечения
упругого
рас
сеяния
(см.
гл.
2).
До
сих
пор
мы
не
учитывали
многокра
тного
рассеяния
в
апер
туру
объектива.
Интерференционное
приближение,
основан
ное
на
использовании
соотношения
(1.19в),
предполагает
нали
чие
только
однократного
рассеяния
и,
следовательно,
не
учитывае'г
«многократной
дифракцию>.
Многократная
дифракция
учитывает
ся
динамической
теорией
рассеяния,
но
последняя
применима
лишь
к
кристаллам
с
размерами,
превышающими
те,
о
которых
говорилось
выше.
В
принципе
можно
получить
выражение,
вклю
чающее
рассеяние
в
направлении,
ПРОТИВОПОЛОЖНОМ
по
отноше
нию
к
падающему
пучку,
но
вывод
его
очень
сложен,
и
поэтому
мы
не
будем
его
рассматривать
(см.,
например,
[4J).
Наиболее
§
3.
РАССЕЯНИЕ
НА
IШАЗИАМОРФНЫХ
ТЕЛАХ
61
вероятный
вклад
в
рассеяние
в
апертуру
дает
первое
дифракцион
ное
гало,
так
как
его
полное
угловое
отклонение
меньше,
чем для
последующего
максимума.
Эмпирически
сечение
рассеяния
в
апер
туру
учитывается
следующим
обраЗ0М:
прошедшая
интенсивность
.записывается
в
виде
.
It=Ioe-(~=~,!,
(1.26)
тде
Q'
-
сечение
рассеяния
в
апертуру
-
функция
~Об.
Холи
дей
и
Ивин
[17],
а
также
Холл
[7]
нашли,
что
выражение
(1.26)
вполне
удовлетворительно
определяет
интенсивность.
Но
зна
чения
Q'
оказываются
неожиданно
высокими;
в
работе
[17]
было
найдено,
что
Q'
/Q
~
0,7
(если
учитывать
и
неупругое
рассеяние).
Следует
обратить
внимание
на
то,
что
экспериментально
опре
деленные
сечения
обычно
меньше
рассчитанных
теоретически.
Основную
неопределенность
как
в
случае
упругого,
так
И
в
слу
чае
неупругого
рассеяния
вносит
коллективное
рассеяние.
Поэтому
рекомендуется
ПОЛЬЗ0ваться
эмпирическим
соотношение~
(1.26)
так,
как
описано
в
работе
[17].
При
полуколичественнои
()ценке
контраста
на
изображении
следует
ПОЛЬЗ0ва
ться
абсолют
ными
сечениями.
Любые
изменения
характера
процессов
u
рас
сеяния,
ведущие
к
уменьшению
интенсивности,
рассеяннои
вне
.апертуры
объектива,
приводят
к
соответствующему
уменьше
нию
контраста
на
изображении.
Очевидно,
что
наличие
многократ
ного
рассеяния
также
уменьшает
контраст.
После
всего
изложенного
выше
имеет
смысл
рассмотреть
кар
тины
рассеяния
для
некоторых
простых
<<аМОРфныХ»
u
ма
териалов,:
На
фиг.
19
показаны
картины
рассеяния
в
заднеи
фокально~
плоскости
на
углероде,
полиэтилене,
коллодии
и
углероднои
реплике
оттененной германием.
Все
они,
по
существу,
представ
ляют
с~бой
дифракцию
от
выбранной
площади
образца.
Для
сравнения
рядом
приведены
размеры
апертурных
диафрагм
-объектива
в
50, 30
и
20
.7ItК.
НИ
В
одном
из
приведенных
материалов
первое
гало
не
проходит
вместе
с
центральным
лучом
СКВО3Ь
апертуру.
б
Максимумы
в
случае
пленок
И3
коллодия
и
углерода
олее
{<диФФузны»,
чем
в
остальных
двух
случаях.
На
электронных
мик
рофотографиях
этих
материалов
не
обнаруживаются
детали
кристаллического
строения,
так
как
размеры
кристаллов
в
дан
ном
случае
меньше
до
[см.
(1.23б)].
В
случае
углеродных
реплик,
оттен;енных
германием
(фиг.
19,
г),
максимумы
интенсивности
более
резки,
и
это
говорит
о
том,
что
кристаллиты
образца
имеют
большие
размеры.
Надо
отме
тить,
что
на
фиг.
19,
г
не
видно
углеродного
гало.
Это
обычное
явление
в
случае
дифракции
на
смеси
двух
фаз,
И3
которых
одна
более
упорядочена,
чем
другая.
На
основании
картины
рассея-
