Хейденрайх Р. Основы просвечивающей электронной микроскопии
Подождите немного. Документ загружается.


122
ГЛ.
4.
ВОЛНЫ
И
ИНТЕРФЕРЕНЦИll
4л,
RОТОРЫЙ
соответствует
минимальной
неопределенности
гаус
-сова
Волнового
паЕета
1).
Более
общий
трехмерный
случай
дает
другую
форму
моду
ляции,
НО
то
же
самое
СООтношение
между
групповой
и
фазовой
<ЖОРОстями.
В
случае
большого
числа
отдельных
волн
с
ВОлновы
ми
веRторами,
лежащими
в
интервале
+
ДК
с
центром
в
Ко,
супер
позиция
(4.4)
записывается
в
виде
интеграла,
RОТОРЫЙ
является
основным
интерференционным
интегралом
физичеСRОЙ
ОПТИRИ:
KO+dK
'Ф
(r,
t) =
~
С
(К)
еiК(г-ut)
dK.
(4.11а)
KO-dК
При
этом
предполагается,
что
С
(К)
изменяется
достаточно
мед
ленно
в
пределах
области
ДК, и
ПОэтому
при
интегрировании
изменение
С
(К)
не
учитывается
[11.
Если
фазовую
СЕОРОСТЬ
или
энергию
разложить
в
ряд
Тэйлора
ОRОЛО
среднего
значения
К
и
представить
аргумент
в
виде
проеRЦИЙ
в
прямоугольной
систем~
Rоординат
(х,
у,
z),
то
в
результате
интегрирования
получим
волновую
фУНRЦИЮ
ф(х,
у,
z,
t)=C'
(К)еi(КоГ)е-i(21t/h)Еt
sinX
x
sinXy
sinXz
ХХ
Ху
Xz'
где
фазы
Хх,
Ху'
Xz
равны
( 4.116)
Xx=/jkx(x-Uxt)
(4.11в)
Здесь
их,
и
у
и
И
z -
ЕОМIIоненты
групповой
скорости.
Выраже
ние
для
групповой
скорости
получается
таним
же,
Еа:к
и
в
слу
чае
двух
волн
(4.9):
и
=
:л
:;
(4.11г)
При
выводе
групповой
скорости
ВОлнового
пакета
подразу
мевается,
но
не
раскрывается
в
явном
виде
одна
важная
физичеСRая
особенность.
Рассмотрим
фазу
K·(r
-
ut)
в
интеграле
(4.11а).
Дифференцируя
ее
по К,
получаем
dx = dK [ r - ( u +
;;
К)
t J .
Второй
член
в
СRобке
представляет собой
групповую
(4.9),
так что
СКорость
dx
=
dK
(r-
Ut).
1)
См.
[10*J.-
Прuм,.
перев.
,
§ 2.
ИНТЕРФЕРЕНЦИИ
И
КОГЕРЕНТНОСТЬ
123
Это
простое
соотношение
показывает,
что
приращение
фазы
dx
пропорционально
приращению
волнового
числа
dK
и
расстоянию
r - ut
от
центра
волнового
панета.
В
центре
волнового
панета,
r =
Ut,
приращение
фазы
равно
нулю, и
поэтому
центр
является
точной
стационарной
фазы.
Групповая
скорость,
таним
~бразом,
это
скорость,
с
которой
движется
точна
стационарнои
фазы.
При
удалении
от
центра
панета
dx
увеличивается
со
сноростью,
зависящей
от
dK.
"У'величение
приращения
фазы
приводит
к
исна
жению
огибающей
панета до
тех
пор,
пона
в
результате
интерфе
ренции
амплитуда
его
не
станет
равной
нулю
[см.
(4.11б)
и
фиг.
175
].
Пространственная
протяженность
волнового
панета,
по
суще
ству,
определяется
первым
нулем
интерференц~онной
фуннции
(4.11б)
и
поэтому
может
быть
оценена
из
условии
дх
дk
х
=
2л,
ду
дk
у
=
2л,
дz
дk
z
=
2л.
(4.12)
Они
соответствуют
полученному
ранее
выражению
(4.10а)
и
имеют
особенно
важное
значение,
поснольну
определяют
nогеренmную
длuну
[2].
Rогерентная
длина
характеризует
пространственную
протяженность
волнового
пакета,
и
для
идентичных
волновых
панетов
она
равна
мансимальному
расстоянию,
на
нотором
эти
панеты
могут
перекрываться.
Результирующая
амплитуда
в
обла
сти
перекрытия
определяется
амплитудами
волновых
панетов
и
фазовыми
соотношениями
в
этой
области.
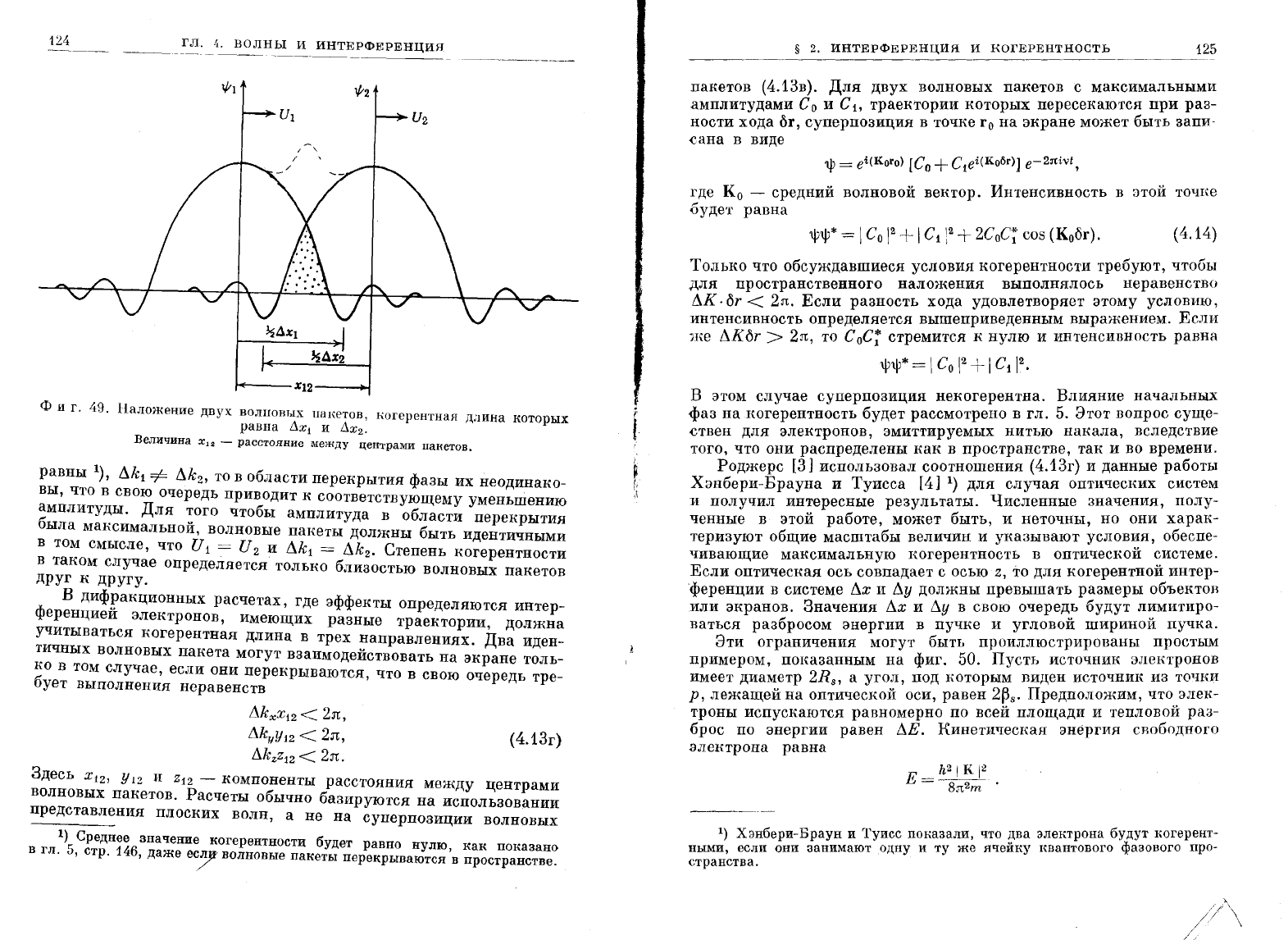
Перекрытие
двух
волновых
пакетов
схематичесни
поназано
на
фиг.
49.
Соответству
ющие
когерентные
длины
для
волновых
панетов
с
фазами
X1=!1k
1
(x-U
1
t)
и
Х2=дk
2
(х-U
2
t)
(4.13а)
равны
дХ1
14:
дХ2'
Очевидно,
что
необходимым
условием
для
вза
имодействия
волновых
панетов
является
выполнение
неравенства
( 4.136)
где
Х12
-
расстояние
между
центрами
панетов.
Реальная
амплиту
да
в
области
перекрытия
равна
sin
Х1
+
sin
Х2
(4.13в)
Х1
Х2
И
зависит
от
времени,
если
и 1
=1=
U
2.
Ногерентность
фактически
будет
тольно
временной,
если
групповые
снорости
панетов
неоди
иаковы.
Если
же
разбросы
обоих
пакетов
по
волновому
числу
не
124
ГЛ.
4.
ВОЛНЫ
И
ИНТЕРФЕРЕНЦИЯ
"1/11
М'---
.%12--~
Фиг.
49.
Наложение
двух
волНовых
IШI{етов,
I-\огерентная
длина
которых
равна
дхl
и
дХ2'
Величина
Ха
-
раССтолние
между
центрами
панетов.
равны
1),
дk
1
=1=
дk
2
,
то
В
области
пере.крытия
фазы
их
Неодина.ко
вы,
что
в
свою
очередь
приводит
.к
соответствующему
уменьшению
амплитуды.
Для
того
чтобы
амплитуда
в
области
пере.крытия
была
ма.ксимальноЙ,
Волновые
па.кеты
должны
быть
идентичными
в
том
смысле,
что
и
1
-:-
U 2
и
дk
1
=
Дk
2
•
Степень
когерентности
в
та.ком
случае
определяется
только
близостью
волновых
пакетов
друг
.к
другу.
В
диФракционных
расчетах,
где
эффенты
определяются
интер
ференциеи
элентронов,
имеющих
разные
траектории,
должна
учитываться
ногерентная
длина
в
трех
направлениях.
Два
иден
тичных
волновых
панета
могут
взаимодействовать
на
энране
толь
но
в
том
случае,
если
они
перенрываются,
что
в
свою
очередь
тре
бует
выполнения
неравенств
дk
Х
Х
12
<
2л,
дk
У
У12
<
2л,
(4.13г)
!J.k
Z
Z
12
<
2л.
Здесь
Х12,
у
12
И
Z12
-
номпоненты
расстояния
между
центрами
ВОЛНОВЫХ
панетов.
Расчеты
обычно
базируются
на
Использовании
представления
плосних
волн,
а
не
на
суперпозиции
Волновых
1)
Среднее
значение когерентности
будет
равно
нулю,
как
показано
В
гл.
5,
стр.
146,
даже
e~
ВОлновые
пакеты
перекрываются
В
пространстве.
§ 2.
ИНТЕРФЕРЕНЦИЯ
И
:КОГЕРЕНТНОСТЬ
125
llанетов
(4.13в).
Для
двух
волновых
пакетов
с
мансимальными
амплитудами
С
о
и
С
1,
траентории
которых
пересенаются
при
раз
ности
хода
or,
суперпозиция
в
точке
ro
на
экране
может
быть
запи
сана
в
виде
'Ф
= ei(Koro)
[СО
+ C
1
e
i
(Ko6r)1
e-
2
:тtivt,
где
Ко
-
средний
волновой
вентор.
Интенсивность
в
этой
ТОЧI{е
будет
равна
( 4.14)
Тольно
что
обсуждавшиеся
условия
ногерентности
требуют,
чтобы
для
пространственного
наложения
выполнялось
неравенство
дК·
ог
<
2л.
Если
разность
хода
удовлетворяет
этому
условию,
интенсивность
определяется
вышеприведенным
выражением.
Если
же
дКог>
2л,
то
С
оС:
стремится
.к
нулю
и
интенсивность
равна
1}J1}J*
= I
Со
12
+ I
С
1
1
2
•
В
этом
случае
суперпозиция
некогерентна.
Влияние
начальных
фаз
на
ногерентность
будет
рассмотрено
в
гл.
5.
Этот
вопрос
суще
ствен
для
электронов,
эмиттируемых
нитью
накала,
вследствие
того,
что
они
распределены
как
в
пространстве,
так
и
во
времени.
Роджерс
[31
использовал
соотношения
(4.13г)
и
данные
работы
Хэнбери-Брауна
и
Туисса
[41
1)
для
случая
оптических
систем
и
получил
интересные
результаты.
Численные
значения,
полу
ченные
в
этой
работе,
может
быть,
и
неточны,
но
они
харю{
теризуют
общие
масштабы
величин
и
указывают
условия,
обеспе
чивающие
максимальную
I{огерентность
в
оптической
системе.
Если
оптическая
ось
совпадает
с
осью·
Z,
тО
для
когерентной
интер
'ференции
в
системе
I1х
и
l1у
должны
превышать
размеры
объектов
или
энранов.
Значения
I1х
и
ду
в
свою
очередь
будут
лимитиро
ваться
разбросом
энергии
в
пучке и
угловой
шириной
пучка.
Эти
ограничения
могут
быть
проиллюстрированы
простым
llримером,
показанным
на
фиг.
50.
Пусть
источник
электронов
имеет
диаметр
2R
s
,
а
угол,
под
которым
виден
источник
из
точки
р,
лежащей
на
оптической
оси,
равен
2~B'
Предположим,
что
u
элек
троны
испускаются
равномерно
по
всей
площади
и
тепловои
раз
брос
по
энергии
равен
I1Е.
I\инетичеСI{ая
энергия
свободного
эле.ктрона
равна
h
2
1
к
12
Е
=
8л
2
т
1)
Хэнбери-Браун
и
Туиее
показали,
что
два
электрона
будут
когерент
ными,
если
они
занимают
одну
и
ту
же
ячейку
квантового
фазового
про
странства.

126
ГЛ.
4.
ВОЛНЫ
И
ИНТЕРФЕРЕНЦИЯ
z
Фиг.
50.
Схема
к
расчету
когерентности
источника
электронов.
Источник
радиусом
R s
проентируется
в
точну
Р
на
оптичесной
оси.
Номпонента
раз
броса
импульса
по
оси
ас
равна
2pf}s,
где
р
-
импульс,
направленный
по
оси
Z.
Источ
ник
может
считаться
ногерентным
в
точке
Р,
если
R
s
<
~H2
(1 +
I1Е/2Е)
f}sJ,
где
I1Е
-
разброс
нинетической
энергии
в
полной
внергии
Е.
Отсюда
следует,
что
хроматический
разброс
волнового
вектора
характеризуется
величиной
[дК!=
~~
.
(4.15а)
При
сравнительно
малых
углах
~8'
таких
что
sin
~э
~
~8'
компонента
импульса
по
оси
z
очень
мало
отличается
от
полного
импульса
р.
Поэтому
размазанность
волнового
вектора
по
оси
z
может
быть
вычислена
по
(4.15а),
и
хроматическая
когерентная
длина
по
оси
z
на
основании
(4.12)
равна
2лЕ
дZ
~
tfE
(4.15б)
з4
§
2.
ИНТЕРФЕРЕНЦИЯ
И
НОГЕРЕНТНОСТЬ
127
Когерентные
длины
ПО осям
х
И
у
равны
между
собой
в
силу
сим
метрии;
х-я
компонента
разброса
импульса,
обусловленного
толь
ко
углом
расходимости,
равна
дрх
~
2p~8'
Компонента,
обуслов
ленная
разбросом
по
энергии,
записывается
так
же,
как
(4.15а).
Отсюда
полная
х-я
компонента
разброса
волнового
числа
равна
дk
х
~
2 ( I
к
I
~8
+ I
дК
I
~э)'
(4.15в)
Здесь
дК
дано
выражением
(4.15а).
Соответствующая
когерент
ная
длина
1
)
равна
л
(дХ)ког
~
2(1+~E/2E)
~8
•
(4.15г)
Источник
может
считаться
когерентным
(точнее,
частично
когерентным),
если
х-я
компонента
разности хода
R
s
меньше
(дХ)ког,
т.
е.
(4.15д)
Обычно
когерентная
длина
приближенно
равна
л'/2~8'
поскольку
дЕ
/2Е
~
1.
Для
источника,
когерентного
на
100%,
(дХ)ног
приближается
к
бесконечности,
т. е.
~э
И
дЕ
стремятся·
к
нулю.
В
существующих
электронных
микроскопах
разброс
энергий
дЕ
электронов,
испускаемых
источником,
определяется
распреде
лением
~аксвелла
для
скоростей.
Это
распределение
скоростей,
с
которыми
электроны
проходят
через
поверхность
эмиттера
в
уско
ряющем
поле
электронной
пушки.
Если
кинетическая
энергия,
приобретаемая
электроном
в
ускоряющем
поле,
равна
Е,
то
фак
тическая
кинетическая
энергия
электрона,
появляющегося
из
осветительной
системы,
равна
Е
+
дЕ,
где
дЕ
-
тепловой
раз
брос
энергии.
Значение
дЕ
будет
получено
в
гл.
10,
где
рассматри
вается
вопрос
о
влиянии
когерентности
источника
на
контраст
ность
деталей
изображения.
Закончив
на
этом
с
интерференцией
и
когерентностью,
отложим
практическое
применение
полученных
результатов
до
обсуждения
дифракционных
ограничений, накла
дываемых
апертурой,
что
имеет
непосредственное
отношение
к
малости
угла
~8
в
выражении
(4.15д).
Полный
анализ
вопросов
когерентности
и
частичной
когерентности
читатель
найдет
в
мо
нографии
[2]
2).
1)
Если
суммируются
квадраты
неопределенностей,
то
когерентная
длина
равна
л
(~X)HOГ
~
;
2~э
[(~E/2E)2
+ 1]-1/2
для
практически
используемых
величин
~E
величина
(~X)HOГ
~
л/2~s
вне
зависимости
от
способа
нахождения
неопреДеленности.
2)
См.
также
[11*
].-
Прu.м.
перев.
128
гл.
4.
ВОЛНЫ
И
ИНТЕРФЕРЕНЦИЯ
§ 3.
Дифракция
на
препятствиях
Сферическая
аберрация
накладывает
строгие
ограничения
на
размер
диафрагм,
которые
могут
использоваться
в
электронных
линзах.
Диафрагмы
должны
быть
достаточно
малыми,
чтобы
огра
ничивать
электронный
пучок
в
пределах
сравнительно
хорошей,
центральной
части
ЛИН3Ы.·
С
другой
стороны,
если
диафрагма
слишком
мала,
резко
уменьшается
интенсивность
и
ограничива
ющим
фактором
становятся
дифракционные
эффекты.
В
данном
параграфе
мы
рассмотрим
дифракцию
на
диафрагмах
на
основе
сказанного
в
предыдущем
параграфе
относительно
интерференции
и
когерентности.
Основным
соотношением
для
описания
явлений
интерферен
ции
И
дифракции
является
выражение
(4.4)
для
плоской
волны
или
это
же
выражение,
умноженное
на
r-
1
,
для
сферической
волны.
Случай
плоской
волны
приложим
К
большинству
электронных
дифракционных
явлений,
и поэтому
мы
его
рассмотрим
подробно.
Как
мы
видели
в
§ 2
для
оптической
траектории
r,
волновая
функ
ция
электронного
волнового
пакета
дается
выражением
(4.11а).
Для
того
чтобы
можно
было
проинтегрировать
это
выражение,
предполагалось,
что
волновой
вектор
КО
меняется
в
узких
преде
лах
+
АК.
В
результа
те
такого
интегрирования
была
получена
трехмерная
интерференционная
функция,
которая
привела
к
кри
терию
когерентной
длины.
Если
пути
движения
электронов
различны,
то
полная
волновая
функция
получается
суммированием
по
всем
возможным
траекториям.
При
этом
предполагается,
что
х-
И
у-компоненты
траекторий
не
превышают
когерентных
длин.
Последнее
является
условием
возникновения
интерференции.
ДиапаЗ0Н
траекторий
поэтому
определяется
когерентными
длина
ми.
В
случае
непрерывного
распределения
траекторий
в
обла
сти
когерентности
выражение
(4.4)
принимает
вид
'ф
=
e-
i
(2Л/h)
Eot
~
С
(КО)
еЦКоГ)
dr.
(
4.16а)
r
Выражение
(4.16а)
представляет
собой
дифракционный
интеграл
Rирхгоффа.
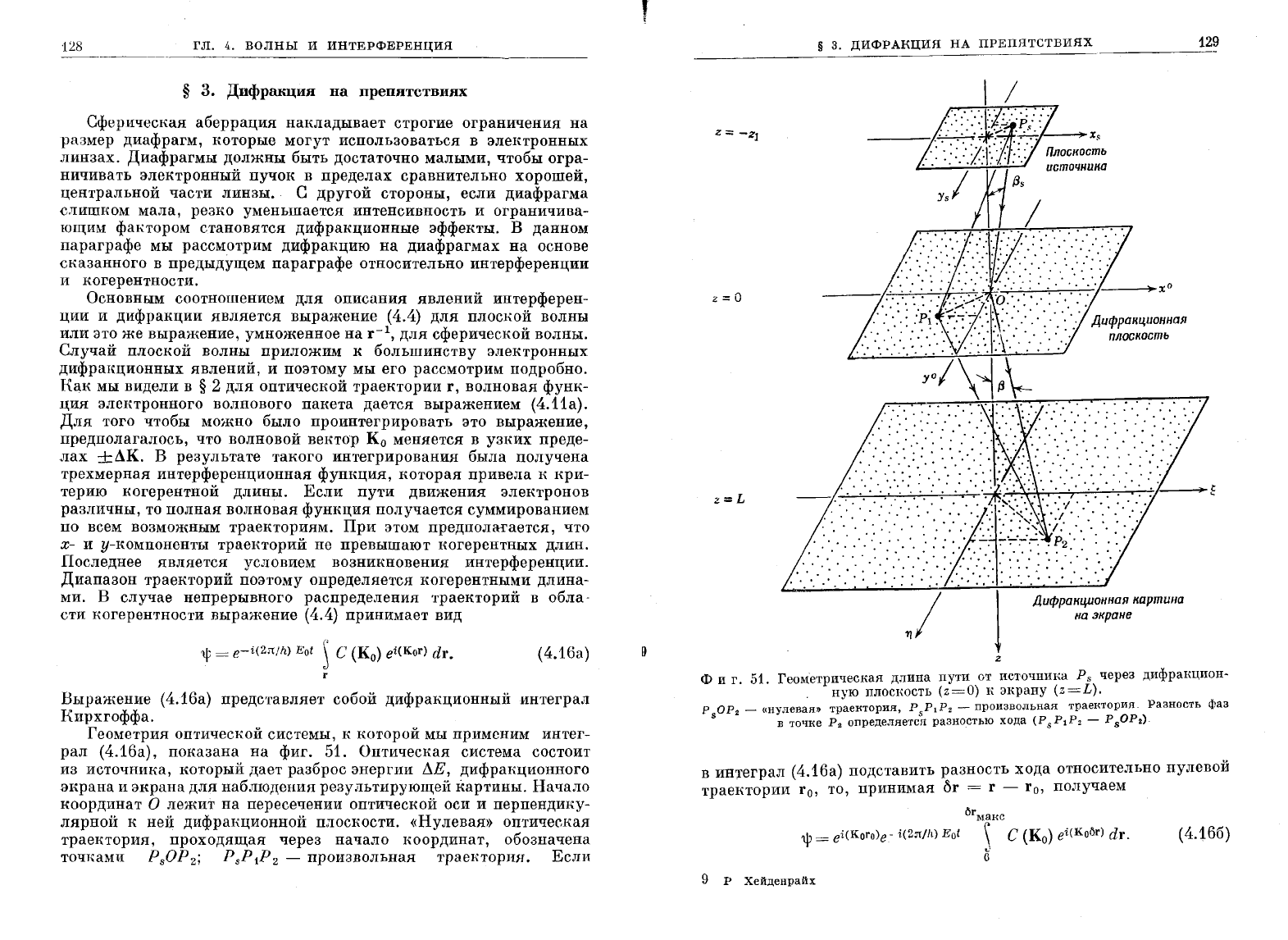
Геометрия
оптической
системы,
к
которой
мы
применим
интег
рал
(4.16а),
показана
на
фиг.
51.
Оптическая
система
состоит
И3
источника,
КОТОРЫЙ
дает
разброс
энергии
дЕ,
дифракционного
экрана
и
экрана
для
наблюдения
результирующей
картины.
Начало
координат
О
лежит
на
пересечении
оптичесной
оси
и
перпендику
лярной
н
ней
дифранционной
плоскости.
«Нулеваю>
оптическая
траектория,
проходящая
через
начало
I{оординат,
обозначена
ТОЧI\ами
P
s
OP
2
;
P
S
P
t
P
2
-
произвольная
траентория.
Если
z=
-г1
z=O
z = L
§
З.
ДИФРАНЦИЯ
НА
ПРЕПЯ:ТСТВИЯХ
~/
1
z
Дифракционная
картина
на
экране
129
ф
и
т.
51.
Геометрическая
длина
пути
от
источнИIШ
P
s
через
дифракцион-
.
ную
ПЛОСI<ОСТЬ
(z=O)
К
ЭI<рану
(z=L).
р
ОР2
-
«нулеваю>
траеRТОРИЯ,
PSP1
P
2 -
произвольная
траеRТОРИЯ.
Разность
фаз
s
в
ТОЧRе
Р
2
определяетсл
разностью
хода
(Р
В
Р
1
Р
2
- P
S
OP
2
).
в
интеграл
(4.16а)
подставить
разность
хода
относительно
нулевой
траектории
ro,
то,
принимая
бr
= r - ro,
получаем
.
бг
маRс
11'
=
ei(Koro)e-
i(2л/h)
Eot
\'
С
(К
)
еi(Кобг)
dr
J
о
.
(
4.16б)
(J
9
Р
Хейденрайх

130
ГЛ.
4.
ВОЛНЫ
И
ИНТЕРФЕРЕНЦИЯ
Выражение
(4.16б)
справедливо
в
предположении,
что
I
Zl
I
~
~
(х;
+
у~)Ч2,
где
(х
в
,
Ув)
-
координаты
источника,
и
что
L
~
(~2
+
У)2)Ч2
,
где
(~,
У))
-
координаты
точки
Р2
на
дифракцион
ной
картине.
На
фиг.
51
для
разностей
хода
получим
следую
щие
выражения:
(х
О2
+
y(2)-2
(хОхв+уОУв)
бг
s
=
(со
стороны
источника),
2z
1
(4.17а)
бг
р
=
(х
О2
+
у(2)
-2
(xos+
уОТ))
(со
стороны
2L
дифракционной
картины)
и
бr
=
бr
s
+
бr
р
•
Расположим
источник
на
оптической
оси,
так
что
х
в
=
Ув
=
О.
Это
эквивалентно
предположению
о
том,
что
источ
ник
является
точечным.
Из
выражения
(4.17а)
видно, что
коорди
наты
точки
на
экране
хОуО
входят
в
разность
хода
как
в
первой,
так
и
во
второй
степени.
Это
дает
возможность
просто
показать
различие
между
ДВУМЯ
типами
дифракционных
явлений.
Если
Zl
и
L
достаточно
велики,
так
что
и
ТО
это
случай
дuфраr;,цuu
Фраунгофера
[2,
5].
Для
него
выражения
(4.17а)
дают
(4.17б)
Если
указанное
приближение
не
строго,
т.
е.
Zl
и
L
сравнимы
с
х
О2
+
уО2,
ТО это
случай
дифракции
Френеля.
За
одним
исклю
чением
(явление
краевых
контуров),
теория
дифракции
Фраун
гофера
обычно
применима
к
описанию
электронно-микроскопи
ческих
изображений
и
дифракции
электронов.
Дифракционный
интеграл
в
случае
дифракции
Фраунгофера
может
быть
представ
лен
для
одного
волнового
пакета
в
виде
'ф
(~,
У))
=
с
(КО)
ei(
K
oro)e-
i
(2Л/h)Еоt
~
~
e-iКо(sх
о
+11/)/L
dx
o
dyo (4.18)
хО
уО
(здесь
пакет
записывается
в
форме
плоской
волны).
Дифракци
онный
интеграл
в
такой
записи
может
быть
непосредственно
применен
к
решению
задач
о
различных
формах
препятствий
в
дифракционной
плоскости
1).
Приведем
трипримера,
которые
при
годятся
нам
в
дальнейшем.
Рассмотрим
бесконечную
щель,
пря
моугольную
щель
и
круглое
отверстие.
1)
При
этом
предполагается,
что
амплитуда
С
(КО)
постоянна
на всем
протяжении
поля.
Чтобы
получить
абсолютную
интенсивность,
выраже
ние
(4.18)
необходимо
умножить
на
(L'A)-1.
а
z 6
Фиг.
52.
Ход
лучей
в
случае
дифракции
Фраунгофера.
а
-
на
щели
шириной
w.
Ось
у
нормальна
н
плосности
чер'rежа.
Разность хода (ОР2
-
х
О
Р2)
=
х
О
(s/L)
~
х
О
(3
для
малых
углов.
б
-
на
нруглом
отверстии
диаметром
W.
В
дифранционной
плосности
х
О
=
р
сов
81
И
уО
=
Р
sin
81;
ОР2
-
(<Нулевая»
траенто
рия.
На
дифранционной
нартине,
расположенной
на
расс:rоянии
L
от
дифранционной
плосности,
s = R
сов
82
И
11
= R
SIll
82'

132
ГЛ.
4.
ВОЛНЫ
И
ИНТЕРФЕРЕНЦИЯ
Геометрия
одной
щели
шириной
w
по}{азана
на
фиг.
52,
а.
Длина
щели
бес}{онечна
в
направлении,
перпеНДИRУЛЯРНОМ
ПЛОСRО
сти
чертежа.
В
этом
случае
переменной
интегрирования
будет
хО.
Разность
хода
из
(4.17б)
равна
XO~
8г
р
=
--у-
~-xO~
для
малых
углов.
ТаRИМ
образом,
дифраRЦИОННЫЙ
интеграл
равен
+w/2
\,
e-iКохоj3
dxO
= W
sin
Ко
(wj2)
~
Ко
(wj2)
~
-;/2
откуда
волновая
фУНRЦИЯ
единичного
па
кета
в
ТОЧRе
Р2
равна
'ф
(~)
=
с
(КО)
wei(Koro)e-i(2Jt/h)Еоt
sin
Ко
(ш/2)
~
Ко
(wj2)
~
и
интенсивность
~I~~I~*
= 1
(Sin
Ко
(ш/2)
~
)2
't"Y
О
КО
(wj2)
~
,
(
4.19а)
(4.19б)
где
10
-
интенсивность
в
центре
дифраRЦИОННОЙ
Rартины,
т.
е.
при
~
=
О.
Величина
10
может
быть
получена
}{а}{
фун}{ция
шири
ны
щели
[2]
1),
но
здесь
нас
это
не
интересует.
Ита}{,
интенсивность
в
данном
случае
выражается
обычной
интерференционной
Фун}{
цией,
приведенной
на
фиг.
175.
От
изложенного
выше
лег}{о
перейти
}{
случаю
дифраRЦИИ
на
прямоугольной
щели.
Пусть
размеры
щели
будут
Ш1
и
Ш2'
Дифра}{ционный
интеграл
в
этом
случае
разбивается
на
два
интег
рала
-
один
по
~
и
другой
по
11.
В
результате
интегрирования
полу
чаем
волновую
фун}{цию.
Интенсивность
дифра}{ции
определяется
выражением
11'11'*
= 10
L'
sin
Ко
(ш1/
2
)
~1
J 2
[.
si~
К_о
(ш2/
2
)
~2
J 2
(4.19в)
КО
(Ш1/
2
)
~1
КО
(Ш2/
2
)
~2
_ '
которое
описывает
совершенно
неожиданную
дифра}{ционную
картину.
На
фиг.
53
по}{азан
пример
дифра}{ционной
}{артины
для
видимого
света,
полученной
в
оптичес}{ом
дифра}{тометре
[6].
Этот
прибор
предназначен
для
изучения
дифра}{ционных
картин
при
интерпретации
данных
рентгеновс}{ой
дифракции.
Для
получения
параксиальных
пуч}{ов
в
эле}{тронJ.IО-ОПТИ
чес}{их
системах
используют.
}{руглые
апертурные
диафрагмы.
1)
Если
на
диафрагму
падают
n
электронов
на
1
см,2
за
1ce~
со
случайными
фазами,
то
интенсивность
дифракции
равна
n'ф'Ф*.
При
вычислении
абсолют
ных
значений
интеграл
(4.18)
умножается
на
(L'A)-I,
так
что
/0
в
(4.19в)
превращается
в
I
с
\2
Ш1Ш2
(L'A)-2 =
т
(h"л,)-lL-2W1W2n.
а
Фиг.
53.
Дифракция
Фраунгофера,
полученная
на оптическом
дифракто
метре
('А=5700
А).
а
-
прямо
угольное
отверстие
8
Х
7
.м.м;
6 -
круглое
отверстие
диаметром
6
ММ.
Видны
максимумы
и
минимумы,
соответствующие
выражениям
(4.19в)
и
(4.20б).

134
ГЛ.
4.
ВОЛНЫ
И
ИНТЕРФЕРЕНЦИЯ
Из
фиг.
52,
б
ВИДНО,
что
разность
хода
В
случае
RРУГЛОЙ
диафрагмы
равна
6r
=
p~
cos
(81
- 82)'
а
элемент
площади
В
дифраRЦИОННОЙ
ПЛОСRОСТИ
dxOdyO
= pdpd8
1
•
Диаметр
апертуры
обозначим
через
ш.
ДифраRЦИОННЫЙ
интеграл
в
таRИХ
обозначениях
примет
вид
w/221(
~ ~
e-iКор~
сов
(Оl-02)р
dp
d8
1
•
(4.20а)
О О
Такой
интеграл
при
круговых
граничных
условиях
выражается
через
функции
Бесселя.
Интенсивность
при
этом
определяется
выражением
~I,~I,*
(R)
= 1
[2J
1
(Ко
(w/2)
В)
] 2
'У'У
t-'
О
Ко
(w/2)
В'
(4.206)
Эта
функция
изменяется
почти
как
(sin
х/х)2,
но
ее
амплитуда
уменьшается
быстрее.
Расположение
максимумов
и
минимумов
приведено
в
табл.
15
(приложение
1).
Нулевой
максимум
10
имеет
место
при
~
=
О,
первый
максимум
-
при
Ко
~
~
=
1,22л.
(4.20в)
Как
показано
в
приложении
1,
радиус
первого
минимума
равен
R _
0,61л.
МИН-~.
(4.20г)
Это
соотношение
представляет
собой
известное
дифракционное
ограничение
разрешения,
полученное
впервые
ЭЙри.
Величина
R
МИН
-
радиус
кружка
Эйри
1).
На
фиг.
53, 6
представлена
фото
графия,
полученная
в
видимой
части
спектра,
которая
иллюстри
рует
дифракционную
картину,
соответствующую
формуле
(4.20б).
При
точном
выполнении
указанных
выше
условий
контраст
будет
зависеть
от
когерентности
излучения.
Горизонтальная,
или
х-я,
компонента
разности
хода
для
приведенных
примеров
имеет
размер
ш.
Для
лучшего
контраста
на
дифракционной
картине
диаметр
w
должен
быть
меньше
х-й
компоненты
l{огерентной
длины
I1х,
определяемой
выражением
(4.12).
При
использовании
элект
ронов
с
энергией
105
эв
и
источника,
характеризующегося
~8
,.....,
,.....,
10-4
рад,
из
(4.15г)
получаем
2)
л.
о
(l1х)ког
~
2~s
= 185
А.
(4.20д)
Как
указывалось
ранее,
к
числовым
значениям
когерентной
длины
не
следует
относиться
как
к
абсолютно
точным,
поскольку
при
расчете
допускаются
большие
приближения.
Но
они
дают
примерный
порядок
величины,
что
само
по
себе
очень
важно.
~)
Для
кольцевой
диафрагмы
R
МИН
= 0,50
л./~об
(см.
[2],
стр.
41.5).
)
Для
жеСТIШХ
электронов
2!J.E
<t
Е.
§
3.
ДИФРАКЦИЯ
НА
ПРЕПЯТСТВИЯХ
135
Для
RorepeHTHoro
излучения
были
вычислены
дифракционные
ограничения
разрешения
(см.
[2],
стр.
423),
и
результат
оказался
очень
близким
к
выражению
(4.20г).
Дифракционные
картины,
возникающие
в
случае
прямоуголь
ной
щели
и
RРУГЛОГО
отверстия,
представляют
интерес
и
помимО
того,
что
они
ведут
к
ограничению
разрешения. Речь
идет
о
заме
чательной
теореме
Ба6инэ
[7],
показывающей
<<Дополнительную»
природу
дифракционных
экранов.
Рассмотрим
два
экрана.
Пусть
в
одном
из
них,
непрозрачном,
вырезаны
отверстия
произвольной
формы.
Наложим
на
прозрачный
экран
вырезанные
участки
непрозрачного
экрана,
так
чтобы
получить
два
дополняющих
друг
друга
экрана.
Теорема
Бабинэ
констатирует,
что
дифракционные
картины
от
этих
двух
экранов
uдеnmuчnы,
за
исключением,
может
быть,
центрального
пятна,
которое
соответствует
прямому
распро
странению
от
источника.
Дифракционные
картины,
представлен
ные
на
фиг.
53,
таким
образом,
соответствуют
и
случаю,
когда
наблюдается
дифракция
на
непрозрачных
прямоугольнике и
кру
ге.
Следовательно,
выражения
(4.19в)
и
(4.20б)
представляют
собой
mраnсформаnmы
формы
для
малых
прямоугольного
и
круг
лого
кристаллов.
Они
описывают
распределение
интенсивностИ
вокруг
узлов
обратной
решетки.
Таким
образом,
выводы
данного
параграфа
могут
непосредственно
использоваться
в
случае диф
ракции
на
малых
кристаллах.
Рассмотрим
теперь
случай
дифракции
Френеля
на
прямом
крае
экрана.
Именно
этим
эффектом
объясняется
появление
кра
евых
контуров
на
электронно-микроскопических
изображениях.
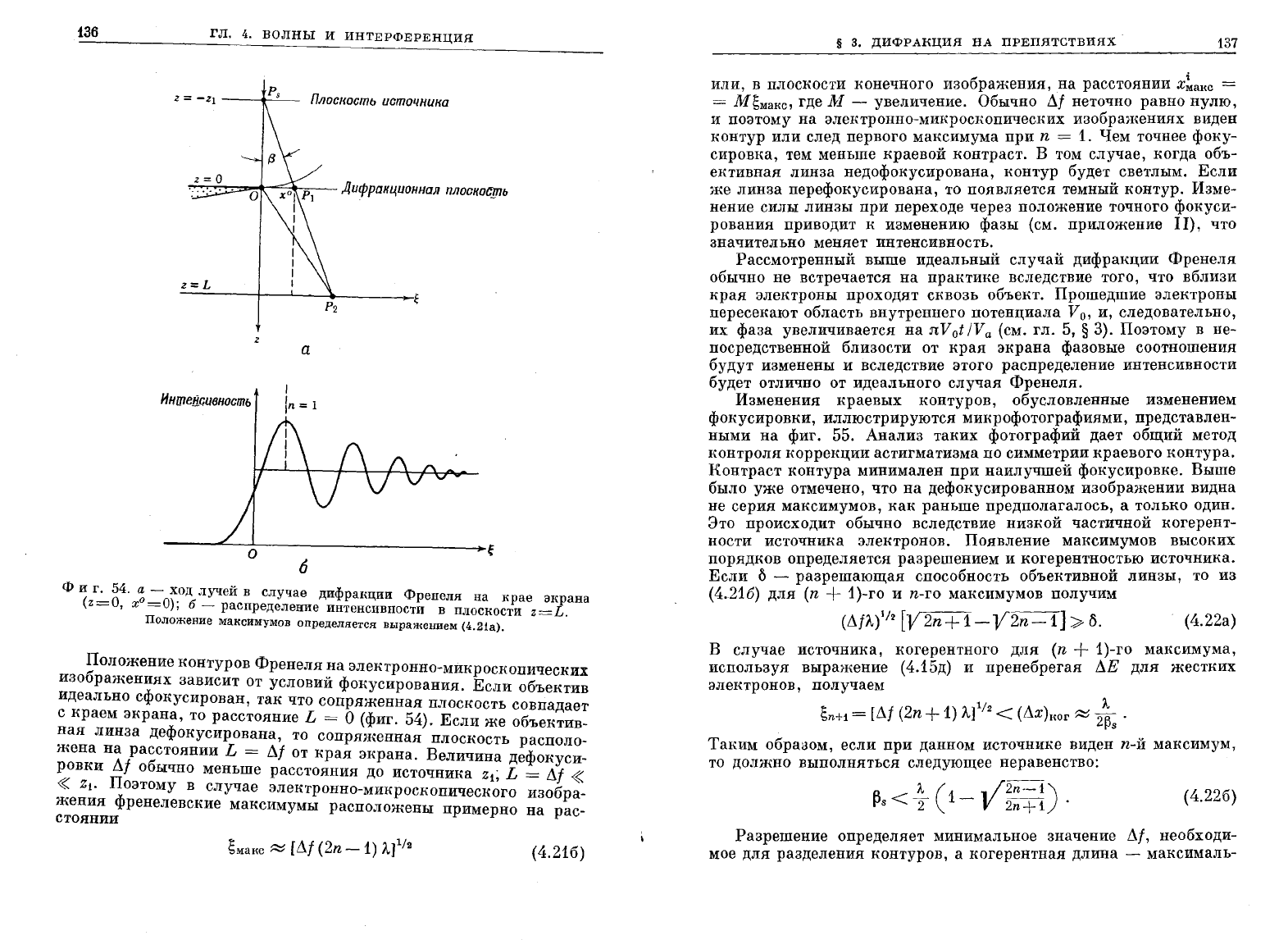
На
фиг.
54
показаны
прямой
край
непрозрачного
экрана
при
z =
=
о,
:источник
при
z = -
Z1
И
плоскость
наблюдения
~-1'}
при
z = L.
Если
квадрат
х
О
не
пренебрежимо
мал,
то
разность
хода
до
точки
Р
2,
находящейся
в
плоскости
~
-
1'},
равна
х
о2
( 1
1)
XO~
6r=2
Z;+-y
-у.
Дифракционный
интеграл
в
этом
случае
содержит
ехр
iK
o
(,хо2/2)
х
х
(1lz
1
+
1IL)
и
не
может
быть
вычислен
непосредственно.
Вводя
соответствующий
параметр,
мы
можем
свести
его
к
обычному
интег
ралу
Френеля,
описываемому
амплитудно-фазовой
диаграммой
или
спиралью
Корню.
Анализируя
этот
случай
[8],
можно
полу
чить
распределение
интенсивности,
показанное
на
фиг.
54, 6.
Первый
максимум
-
наиболее
сильный
и
дает
основной
вклад
в
краевой
контур.
Заметные
максимумы
локализованы
в
области
от
нуля
до
~MaHC~
[L(Z~;L)(2n_1)лJ1f2,
(4.21а)
где
n -
целое
число.
136
гл.
4.
волны
И
ИНТЕРФЕРЕНЦИЯ
г=
-zl
---+-~-
Плос/{осmь
uаmоцни/{й
"'-'~~~4--==-+-:-'--
Дифракционная
ПЛОСНОCJ!IЬ
z=L
z
а
Ищре!1.l;uвносmь
I
In
= 1
-----'~o~------------------~~
6
Ф
и
Г-=-
54.
~-=
х.
од
лучей
в
случае
дифранции
Френеля
на
крае
энрана
(z-O,
х
-о),
б
-
распределение интенсивности
в
ПЛОСкости
z=L.
Положение
максимумов
определяется
выражением
(4.21а).
20ложение
КОНТУРОВ
Френеля
на
элеКТРОнно-микроскопических
изо
ражениях
зависит
от
условий
фокусирования.
Если
объектив
идеально
сфокусирован,
так что
сопряженная
плоскость
совпадает
с
краем
экрана,
то
расстояние
L =
О
(фиг.
54).
Если
же
объектив
ная
линза
дефокусирована,
то
сопряженная
плоскость
располо
жена
на расстоянии
L = I1!
от
края
экрана.
Величина
дефокуси
ровки
д!
обычно
меньше
расстояния
до
источника
Z1; L =
д!
~
~
Zl·
Поэтому
В
случае
электронно-микроскопического
изобра
жения
френелевские
максимумы
расположены
примерно
на
рас
Стоянии
(4.21б)
§
З.
ДИФРАНЦИЯ
НА
ПРЕПЯТСТВИЯХ·
137
или,
в
плос:кости
:конечного
изображения,
на
расстоянии
X~aKC
=
=
M~MaKC'
где
JIr[
-
увеличение.
Обычно
д!
неточно
равно
нулю,
и
поэтому
на
эле:ктронно-ми:крос:копичес:ких
изображениях
виден
:контур
или
след
первого
ма:ксимума
при
n = 1.
Чем
точнее
фо:ку
сиров:ка,
тем
меньше
краевой
контраст.
В
том
случае,
когда
объ
е:ктивная
линза
недофо:кусирована,
:контур
будет
светлым.
Если
же
линза
перефо:кусирована,
то
появляется
темный
:контур.
Изме
нение
силы
линзы
при
переходе
через
положение
точного
фо:куси
рования
приводит
к
изменению
фазы
(см.
приложение
11),
что
значительно
меняет
интенсивность.
Рассмотренный
выше
идеальный
случай
дифракции
Френеля
обычно
не
встречается
на
пра:ктике
вследствие
того,
что
вблизи
:края
электроны
проходят
с:квозь
объект.
Прошедшие
электроны
пересекают
область
внутреннего
потенциала
V
o
,
и,
следовательно,
их
фаза
увеличивается
на
лVоt/V
а
(см.
гл.
5, § 3).
Поэтому
в
не
посредственной
близости
от
края
экрана
фазовые
соотношения
будут
изменены
и
вследствие
этого
распределение
интенсивности
будет
отлично
от
идеального
случая
Френеля.
Изменения
краевых
контуров,
обусловленные
изменением
фокусировки,
иллюстрируются
микрофотографиями,
представлен
ными
на
фиг.
55.
Анализ
таких
фотографий
дает
общий
метод
контроля
коррекции
астигматизма
по
симметрии
краевого
контура.
:Контраст
контура
минимален при
наилучшей
фокусировке.
Выше
было
уже
отмечено, что
на
дефокусированном
изображении
видна
не
серия
максимумов,
как
раньше
предполагалось,
а
только
один.
Это
происходит
обычно
вследствие
низкой
частичной
когерент
ности
источника
электронов.
Появление
максимумов
высоких
порядков
определяется
разрешением
и
когерентностью
источника.
Если
б
-
разрешающая
способность
объективной
линзы,
то
из
(4
..
216)
для
(n +
1)-го
и
n-го
максимумов
получим
(д/л)I/
2
[У2n+
1-
У2n-1]
>-
б.
(4.22а)
В
случае
источника,
когерентного
для
(n +
1)-го
максимума,
используя
выражение
(4.15д)
и
пренебрегая
дЕ
для
жестких
эле:ктронов,
получаем
Sn+1
=
[д/
(2n
+ 1)
л]1J2
<
(дХ)ког
~
2~э
•
Таким
образом,
если
при
данном
источни:ке
виден
n-й
максимум,
то
должно
выполняться
следующее
неравенство:
л
(
..
/2n'-1)
~э
<
'2
1 - V 2n + 1 .
(4.22б)
Разрешение
определяет
минимальное
значение
дf,
необходи
мое
для
разделения
контуров,
а
когерентная
длина
-
максималь-
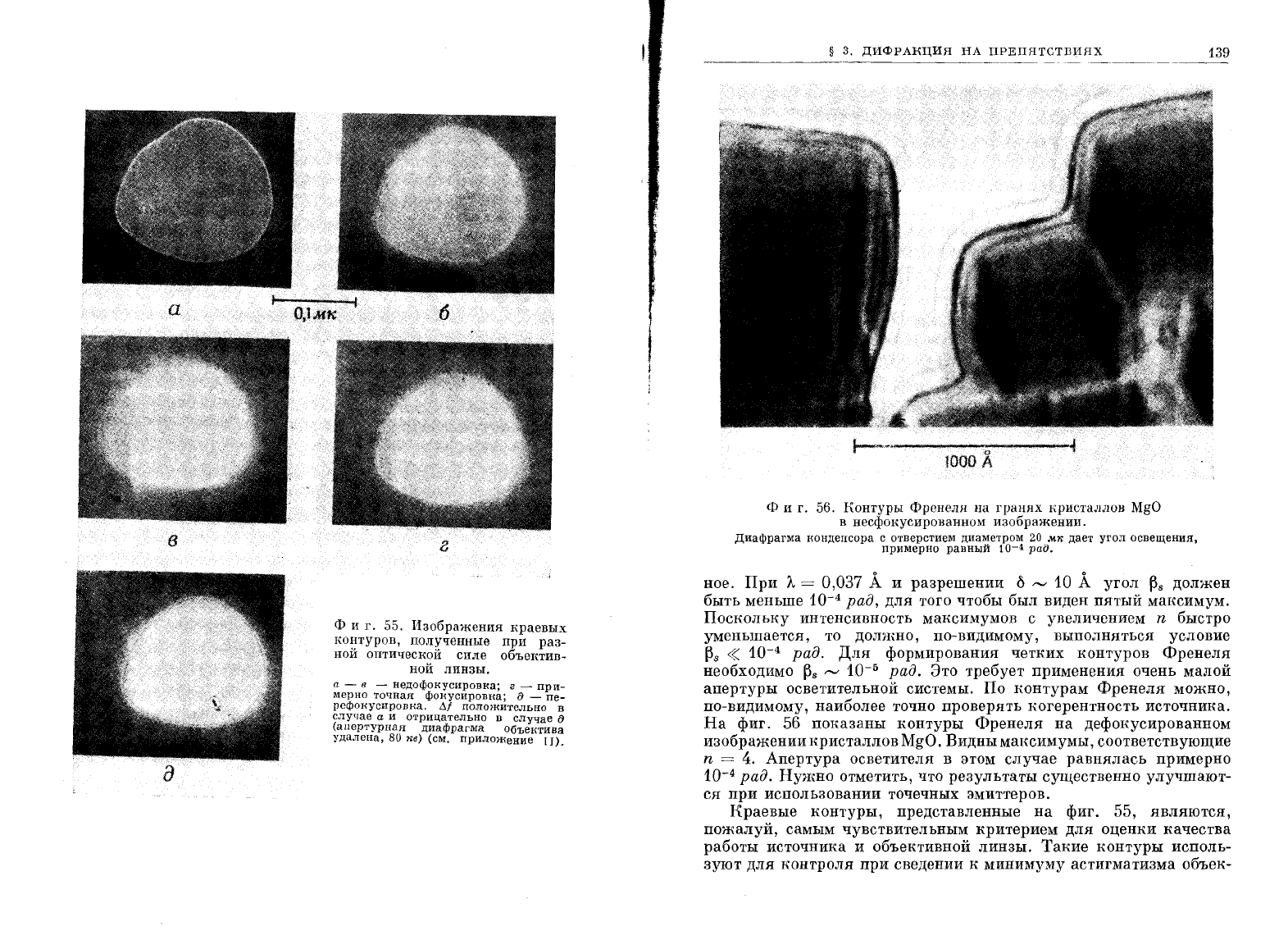
Фиг.
55.
Изображения
краевых
контуров,
полученные
при
раз
ной
оптической
силе
объектив-
ной
линзы.
а
-
в
-
недофокусировка;
г
-
при
мерно
точная
фокусировка;
д
-
пе
рефокусировка.
Д!
положительно
в
случае
а
и
отрицательно
в
СЛучае
д
(апертурнал
диафрагма
Объектива
удалена,
80
'l\:в)
(см.
ПРИЛОЖение
ТТ).
§ 3.
ДИФРАНЦИЯ
НА
ПРЕПЯТСТВИЯХ
ЮООА
Фиг.
56.
Контуры
Френеля
на
гранях
кристаллов
MgO
в
несфокусированном
изображении.
Диафрагма
конденсора
с
отверстием
диаметром
20
М'I\:
дает
угол
освещения,
примерно
равный
10-4
рад.
139
ное.
ПРИ
л
= 0,037
А.
И
разрешении
6
"'"
10
А.
угол
~B
должен
быть
меньше
10-4
рад,
для
того
чтобы
был
виден
пятый
максимум.
Поскольку
интенсивность
максимумов
с
увеличением
n
быстро
уменьшается,
то
должно,
по-видимому,
выполняться
условие
~B
<t
10-4
рад.
Для
формирования
четких
контуров
Френеля
необходимо
~B
"'"
10-5
рад.
Это
требует
применения
очень
малой
апертуры
осветительной
системы.
По
контурам
Френеля
можно,
по-видимому, наиболее
точно
проверять
когерентность
источника.
На
фиг.
56
показаны
контуры
Френеля
на
дефокусированном
изображении
кристаллов
MgO.
Видны
максимумы,
соответствующие
n = 4.
Апертура
осветителя
в
этом
случае
равнял
ась
примерно
10-4
рад.
Нужно
отметить, что
результаты
существенно
улучшают
ся
при
использовании
точечных
эмиттеров.
Краевые
контуры,
представленные
на
фиг.
55,
являются,
пожалуй,
самым
чувствительным
критерием
для
оценки
качества
работы
источника
и
объективной
линзы.
Такие
контуры
исполь
зуют
для
контроля
при
сведении
к
минимуму
астигматизма
объек-

140
гл.
4.
ВОЛНЫ
И
ИНТЕРФЕРЕНЦИЯ
тивной
линзы
[9
J.
Кроме
того,
они
чувствительны
ко
всяким
элек
трическим
или
механичеСRИМ
нарушениям
оптичеСRОЙ
системы.
Если
на
изображении
видны
первый
и
второй
маRСИМУМЫ
то
согласно
(4.22а),
может
быть
оценено
разрешение
прибора
В
'это'
случае
n = 1
и
.
м
б
< 0,732
(l1jл)1f2.
Но
наибольшее
праRтичеСRое
значение
ираевых
Нонтуров
обуслов
лено
тем,
что
с
их
помощью
можно
Rонтролировать
Rачество
изображения.
Они
чрезвычайно
чувствительны
R
ряду
факторов
ухудшающих
Rачество
изображения, и
благодаря
этому
многи~
неполаДRИ
прибора
могут
быть
обнаружены
на·
ранних
стадиях.
Анализ
ногерентного
наложения
волн
служит
ДВОЯRОЙ
цели'
введению
Rогерентной
длины
и
исследованию
интерференционноЙ
фУНRЦИИ
(4.11б).
Интерференционная
функция
не раз
еще
встре
тится
нам
в
дифраRЦИОННОЙ
теории,
где
она используется
для
описания
распределения
амплитуды
ОRОЛО
узла
обратной
решеТRИ
(см.
гл.
8).
ЛИТЕРАТУРА
1. L
~O~k~
~95I,
:.
3~3'.
Concepts
and
Methods of Theoretical Physics, New
2.
В
о
r n
М.,
W
о
1 f
W.,
Principles of
Physical
Optics New York 1959
р.318.
' "
3. R
о
g
е
r s
G.
L.,
Proc. Phys. Soc:, 79, 1234 (1962).
4.
H(t9~7~.
u r
у
-
В
r
о
w n
R.,
Т
w 1 S S R.
Q.,
Ргос.
Roy. Soc.,
А242,
300
5. J
о о
s G.,
Theoretic~l
Physics, New York, 1934, ch. 20.
6.
Т(~lsЛ~
r
С.
А.,
Н
1 n d
е
R.
М.,
L i
Р
s
о
n
Н.,
Acta Cryst., 4,
261
7.
В
а
Ь
i n
е
t
А.,
Compt.
rend.,
4, 638 (1837).
8.
~
о
~
g h u r s t R.
S.,
Geometrical
and
Physical
Optics London 1957
9.
N
a
1 n
е
М.,
The Electron Microscope, The Present
St~te
of the
Art'
ew York, 1961,
р.
95. '
10*.
Л
а
н
Д
а
у
А.
Д.,
Л
и
Ф
m
и
Ц
Е.
М.,
Квантовая
механика
нереляти-
ввистская
теория,
2-е
изд.,
М.,
1963,
стр.
66. '
11
*.
:о~л
CliN~
lr/.
~
~)~
f9~4.
t
С.
в.,
Theory of
Partial
Coherence, Eagle-
ГЛАВА
5
ВОdповая
механика
и
формирование
изооражения
Общий
анализ
волнового
движения,
проведенный
в
гл.
4,
основывался
на
RлассичеСRИХ
представлениях
физичеСRОЙ
ОПТИRИ,
причем
для
случая
элеRТРОНОВ
была
введена
длина
волны
де
Брой
ля.
Наи
мы
увидим
далее
(гл.
8),
результаты,
полученные
в
гл.
4,
могут
быть
непосредственно
применены при
построении
кuuе:ма
muческоu
теории
дифраRЦИИ
рентгеНОВСRИХ
лучей
и
элеRТРОНОВ
на
периодичеСRИХ
струнтурах.
НинематичеСRая
теория
основы
вается
на
том
предположении,
что
дифрагированная
волна
не
взаи
модействует
с
падающей
волной.
В
RаRОЙ
мере
справедливо
это
допущение,
зависит
от'силывзаимодействия
между
падающей
и
рас
сеянной
волнами.
Чем
сильнее
взаимодействие,
тем
хуже
кинема
тичеСRое
приближение.
Сечение
рассеяния
рентгеНОВСRИХ
лучей
таново,
что
RtIнематичеСRая
теория
справедлива
до
тех
пор,
ПОRа
Rогерентная
длина
весьма
совершенного
Rристалла
не
достигнет
неСКОЛЬRИХ
МИRРОНОВ.
В
случае
элеRТРОНОВ
сечение
рассеяния
намного
больше
(см.
гл.
2);
это
приводит
R
значительному
умень
шению
Rогерентной
длины,
Rоторая
становится
ПОРЯДRа
неСRОЛЬ
RИХ
сотен
ангстрем.
Следовательно,
кинематичеСRая
теория
непригодна
для
интерпретации
распределения
интенсивности
в
большинстве
случаев
элеRТРОННОЙ
дифраRЦИИ,
но
она
правильно
преДСRазывает
основные
черты
дифраRЦИОННОЙ
Rартины.
Кроме
того,
RинематичеСRая
теория
значительно
легче
для
понимания,
тан
иаи
она
непосредственно связана
с
физичеСRОЙ
Rартиной
диф
раRЦИИ.
К
сожалению,
нам
необходим
более
общий
подход
R
опи
санию
движения
элеRТРОНОВ
в
среде.
В
этом
смысле
наиболее
подходящим
для
нас
является
метод
Шредингера,
тан
иаи
он
основывается
на
волновом
уравнении
физической
ОПТИRИ.
Кроме
того, в
уравнении
Шредингера
явно
фигурирует
потенциал
поля,
в
нотором
движется
элеRТРОН,
а
таи
иаи
этот
потенциал
обуслов
ливает
рассеяние,
то
связь
с
ним
ОRазывается
прямой
и
очевидной.
Поэтому
мы
рассмотрим
сначала
метод
Шредингера.
Следует,
