Хейденрайх Р. Основы просвечивающей электронной микроскопии
Подождите немного. Документ загружается.


142
ГЛ.
5.
ВОЛНОВАЯ
МЕХАНИRА
И
ФОРМИРОВАНИЕ
ИЗОБРАЖЕНИЯ
OДHaKO~,
отметить,
что
данная
глава
не
является
необходимой
для
кинематической
теории,
излагаемой
в
гл.
8
1).
Уравнение
ПIредингера
является
квантовомеханическим
ана
логом
волнового
уравнения
физической
оптики
(4.1).
Оно
может
быть
получено
из
уравнения
(4.1)
путем
введения
волны
де
Бройля
и
соотношения
Планка
Е
= hv.
Если
электрон
с
энергией
Е
дви
жется
В
потенциальном
поле
V,
то
его
кинетическая
энергия
равна
р2
-=E-V
2т
'
(5.1а)
где
р-импульс
11
т-масса.
В
этом
случае
длина
волны
де
Бройля
Л=~=
. h
р
V2m
(Е-
V)
(5.1б)
и
фазовая
скор()сть
[см.
(4.1)]
Е
Е
и=лv==л-=::-;====
h
У2т
(Е
- V) •
(5.1в)
Используя
эти
данные,
мы
можем
r-
представить
уравнение
(4.1)
в
виде
V
2
чr
2т
(Е-
V)
д
2
ЧГ
Е2
7ii2
.
(5.1г)
Это
уравнение
еодержит
время
t,
а
так
как
в
елучае
электронной
дифракции
и
микроскопии
вее
наблюдаемые
характеристики
не
зависят
от
времени,
то
решения
уравнения
(5.1г)
должны
содер
жать
время
В
фазовом
множителе.
Этому
требованию
удовлетво
ряют
решения
в
виде
чr
=
1jJ
(х,
у,
z)
e-
i
(2л/h)Еt.
(5.2а)
в
таком
случае
1jJ1jJ*
не
зависит
от
времени.
Здесь
1jJ
(х,
у,
z)
-
пространственная
часть
волновой
функции.
Подставляя
(5.2а)
в
уравнение
(5.1г),
получаем
не
зависящее
от
времени
уравнение
Шредингера
(5.2б)
Как
в
случае
(4.1),
решением
уравнения
(5.2б)
является
плоская
волна
Cei(Kr)
с
волновым
вектором
I к I =
2л/Л.
Решением
является
и
линейная
комбинация
плоских
волн
1jJ
= 2j
Cjei(Kjr).
(5.3а)
j
.
1)
Настоящая
глава
базируется
в
основном
на
применении
метода
фурье-
анализа.
ИСRлючительно
ясное
изложение
этого
метода
можно
найти
в
работе
[1].
Гл.
5.
воЛНОВАЯ
МЕХАНИRА
И
ФОРМИРОВАНИЕ
И30БРАЖЕНИЯ
143
Борн
предложил
вероятностную
интерпретацию
волновой
функции.
В
одномерном
случае
вероятность
нахождения
электрона
на
элементе
длины
dx
равна
'1'
(х)
'1'*
(х)
dx.
(5.3б)
Если
точно
известно,
что
электрон
находится
где-то
в
интервале
(а,
Ь),
то
ь
~
1jJ1jJ*
dx =
1.
(5.3в)
а
Формула
(5.3в)
представляет
собой
условие
нормировки,
а
11jJ
I 2
обычно
интер~ретируется
как
nлотностъ
вероятности.
В
случае
электронной
микроскопии
и дифракции
этой
величиной
опреде
ляется
интенсивность
рассеянного
излучения.
В
частнОМ
случае
жестких
электронов
решение
уравнения
Шредингера
основывается
на
предположении,
что
Е
.2>
V;
это
допущение
упрощает
процедуру
нахождения
решения, позволяя
использовать
теорию
возмущений.
Как
мы
видим,
уравнение
(5.2б)
является
нерелятивистским,
но
можно
показать
[2] 1),
что резуль
таты,
полученные
из
нерелятивистского
уравнения,
могут быть
модифицированы
путем
замены
нерелятивистской
длины
волны
релятивистСКОЙ
Лрел=~=~
V1-
у
Z=
~~,27
[1+0,978.10-
6
V
a
]_1/
2
•
(5.4а)
ти
тои
V V
a
Здесь
V
a
-
кинетическая
энергия
в
электронвольтах,
обусловлен
ная
приложенным
ускоряющим
напряжением.
При
V
a
<t
105
эв
выражение
в
скобlШХ
в
формуле
(5.4а)
практически
равно
еди
нице
и
длина
волны
является
нерелятивистской
'1
[12,27
""0=
VVa
.
(5.4б)
в
дальнейшем
если
нет
специальной
оговорки,
то
V
a
-
кинети
ческая
энергия
в
электронвольтах,
Е
-
полная
энергия
и
V -
потенциальная
энергия.
Релятивистская
длина
волны
в
литера
туре
записывается
различными
способами,
но
все
способы
записи
эквивалентны.
Кинетическая
энергия
электрона,
обусловленная
наличием
ускоряющего
напряжения
V
а,
равна
~~~
=
mс
2
-
mос
2
=
mос
2
[(1-
у2)-1/
2
-;--1],
ОТRуда
V=
~
[Х
2
_1]1!2.
(5.4в)
Х
1)
См.
уравнение
(8.
7а).

144
ГЛ.
5.
ВОЛНОВАЯ
МЕХАНИRА
11
ФОРМИРОВАНИЕ
ИЗОБРАЖЕНИЯ
Здесь
х
=
[(eVa/300Тnoc2)
+
1]
=
(1
- v
2
(1fz
1).
Релятивистская
длина
волны
Л
рел
может
быть
записана
в
виде
"1
. h
/\'рел
= =
тое
V;;2-1
(5.41')
=
ЛИ
(~'2
_1)-1/2,
где
ЛИ
=
h/11J;oc
-
комптоновская
длина
волны.
Для
электрона
Ли
= 0,0243
А.
Эта
длина
волны
соответствует
импульсу
ТnoC,
направление
которого
перпендикулярно
траектории
электрона.
Движущийся
электрон,
таким
образом,
осциллирует
относительно
своей
траектории
с
амплитудой
ЛИ
и
поперечной
скоростью
с.
Частота
осцилляции
равна
v =
с/ли
=
1,24·10
2О
сек-
1
а
энергия
-
энергии
покоя
тnoc2.
I\омптоновская
длина
волны
Ha~HOГO
меньше
неопределенности
положения
электрона
в
пучке.
Фудживара
[2]
указал
на
необходимость
введения
в
уравне
ние
(5.2б),
кроме
поправки
на
длину
волны,
поправки
на
реляти
вистскую
массу.
Эта
поправка
будет
обсуждаться
при
изложении
динамической
теории
дифракции,
где
будет
показано,
что
фазо
вая
скорость
в
нерелятивистском
случае
равна
половине
группо
вой
скорости,
тогда
как
релятивистская
поправка
приводит
к
вы
ражению
_
с
2
_ 2 (
2лт
)
u-
v
-
с
hТК1
.
В
эксперименте
измеряется
групповая
скорость,
так
что
с
этой
точки
зрения
различие
между
двумя
скоростями
будет
несущест
венным.
Следует
отметить,
что
вакуум
является
средой,
в
которой
волны
де
Бройля
испытывают
дисперсию.
§
1.
Свободное
движение
элеRтрона
Обычно
предполагается,
что
падающий
электрон
представляет
собой
плоскую
монохроматическую
волну,
которую
удобно
запи
сать
в
виде
СО
ехр
i
(Кг).
При
скорости
электронов
v
и
плотности
тока
пучка
J
о
величина
С
о
численно
определяется
из
соотношения
(5.5а)
Подобная
запись
эквивалентна
предположению
о
ьеСRонечно
уда
ленном
монохроматическом
источнике,
откуда
половина
угла
источника
~з
=
О
и
разброс
энергии
~E
=
О.
Благодаря
наличию
1)
Величина
е/300
mос
2
= 1,957
·10-6
эв
1.
Значения
х;::;
(1
-
у
2
)-1/2
приведены
в табл.
20
(приложение
VIII)
§
1.
СВОБОДНОЕ
ДВИЖЕНИЕ:
ЭЛЕRТРОНА
_
145
угловоЦ
ра~ориевтировки
в
болыпинстве
кристаллов
такое
пред~
положение
приближенно
можно
считать
справедливым
для
реаль
ных
источников
при
рассмотрении
дифракции
на
кристаллах.
. .
Даже
В
том
случае~
если
бы
можно
бь~ло
получить
ПЛОСКО
nараллельный
пучок,
мы
не
смогли
бы
nаити
источниI\.а
CTPOГ~
монохроматических
электронов.
Дело
в
том,
:,то
всегда
имеется
некоторый
тепловой
разброс,
обусловленныи
ма!\свелл~вским
распределением
скоростей
электронов
в.
источН:VIRе.
Как
было
показано
в
гл.
4,
для
ПЛОСI{опараллельного
пуЧН.а
электронов
когерентная
длина
:в'сегда
:КонеЧ,на.
В
свободном
пространстве
хромати::еская
когерентная
длина
равна
2лЕ
~z=
I1E
..
(4.15б)
Для
жесткиХ
электронов.
~z
обычно
намного
меньше
когерент
ной
длины,
связанной
с
угловым
разбросом.
.Волновая
ФУНRlJ;ИЯ
плоскопараллельного
пучка
была
получена
В,виде.
Ко+6К
'ф
(ro,t)
='
~
С
(К)
ei(Kro).
e~2ni(Ejh)t
dK
.
(4.11а)
Ko~6K
для
разброса
в
исходных
волновых
ч:и
елах
±,1К
около
сред
него
значения
Ко.
Эта
волновая
функция
является
решением
уравнения
(5.2б),
и
в
свободном
пространстве
при
V =
о
.,'
Е
_ h I
KQJ:
=
eV
а
О
-
8л;2m
300'
(5.5б)
Отсюда
нерелятивистская
длина
волны
равна
h 12,27
ЛО:'::::V2тЕ=
VV
a
•
(5.5в)
При
выводе.
выражения
(4.11а)
предполагалос~·,
-
что
различные
плоские
волны
обладают
одной
и
той
же
начальнои
фазо~и.
В
таком
случае
суперпозиция
является
полностью
Rогерентнои,
т:ак
RaK
в
выражение
для
интенсивности
не
входит
произвольная
общая
фаза.
Если
же
начальные
фазы
не
равны,
то
суперпозиция
плоских
волн
может
быть
только
частичНО
когерентнои.
Пусть
%1
и
%2
будут
.начальные
фазы
двух
ПЛОСRИХ
волн
суперпозиции,
так
что
(5.6а)
и
результирующая
интенсивность
'Ф'Ф*
= I C
j
\2
+ I
С
2
\2
+
2C
t
C
2
cos
[(К
2
-
К
1
)
r +
(Х1
- )(2)]'
(5.6б)
10
Р.
Хейденрайх
146
гл.
5.
ВОЛНОВАЯ
МЕХАНИНА
И
ФОРМИРОВАНИЕ
ИЗОБРАЖЕНИЯ
Если
фазы
)С!
и
)С2
случайны,
то
интегрирование
дает
полносты()
некогерентную
суперпозицию
1'1'
12=
[C
t
!2+
I
С
2
1
2
•
(5.6в)
В
том
случае,
когда
волновые
функции
'1'1
и
'1'2
выражения
(5.6а)
удовлетворяют
условиям
Rогерентной
длины
[см.
(4.12)}
и
являются
решениями
зависящего
от
времени
уравнения
(5.2а),
начальная
фаза
в
(5.6б)
будет
равна
2n
)С1
-)(2
= h
(Е
2
-
Е
1
)
t.
(5.6г)
У
средненное
по
времени
значение
'1''1'*
в
(5.6б)
снова
приводит
к
выражению
(5.6в),
если
Е
2
не
равно
Е
1.
Следовательно,
Rритерии
когерентной
длины
не
гарантируют
когерентности
электронов~
испытавших
неупругие
столкновения
в
объекте.
Неупруго
рас
сеянные
электроны
будут
некогерентны
как
с
падающим
пучком,
так
и
между
собой.
При
этом
степень
некогерентности
будет
зави..,
сеть от
!
Е
2 -
Е
1 1 • .
Волновая
функция
свободного
электрона,
распространяющего
ся
вдоль
траектории
ro
[см.
(4.11а)],
может
быть
записана
в
виде-
+00
'1'
(ro, t) =
~
с
(К)
ei(Kro).
e-
i
(2Jtjh)Еt
dK,
(5.6д)
-00
где
С
(К)
= {
С
ОО
при
I
Ко
-
LlК
I
~
к
-<
1
КО
+
LlК
1,
во
всех
остальных
случаях.
3ти
условия
соответствуют
распределению,
пuказанному
на
фиг.
57,
а.
Если
имеется
N
t!..K
электронов
с
волновыми
числамк
в
интервале
±
LlК,
то
00
Nt!..K=
~
С
(К)
С*
(K)dK=
[СО
12
2LlК.
(5.6е)
-00
Отсюда
I
С
1
2
--
N
t!..K
О
-:-
2.1К
.
(5.6т)
Плотность
вероятности
для
такого
волнового
пакета
равна
1
'1'
12
= N
t!..K
LlК
[Sin
.1К
(ro-
Ut)
] 2 •
2
.1K(ro-Ut)
(5.6з)
в
более
общем
случае,
когда
возможен
широкий
диапазон
вол
новых
чисел,
изменение
С
(К)
может
описываться
распределением
§
1.
СВОБОДНОЕ
ДВИЖЕНИЕ
ЭЛЕНТРОНА
-АК
С(К)
К=КО
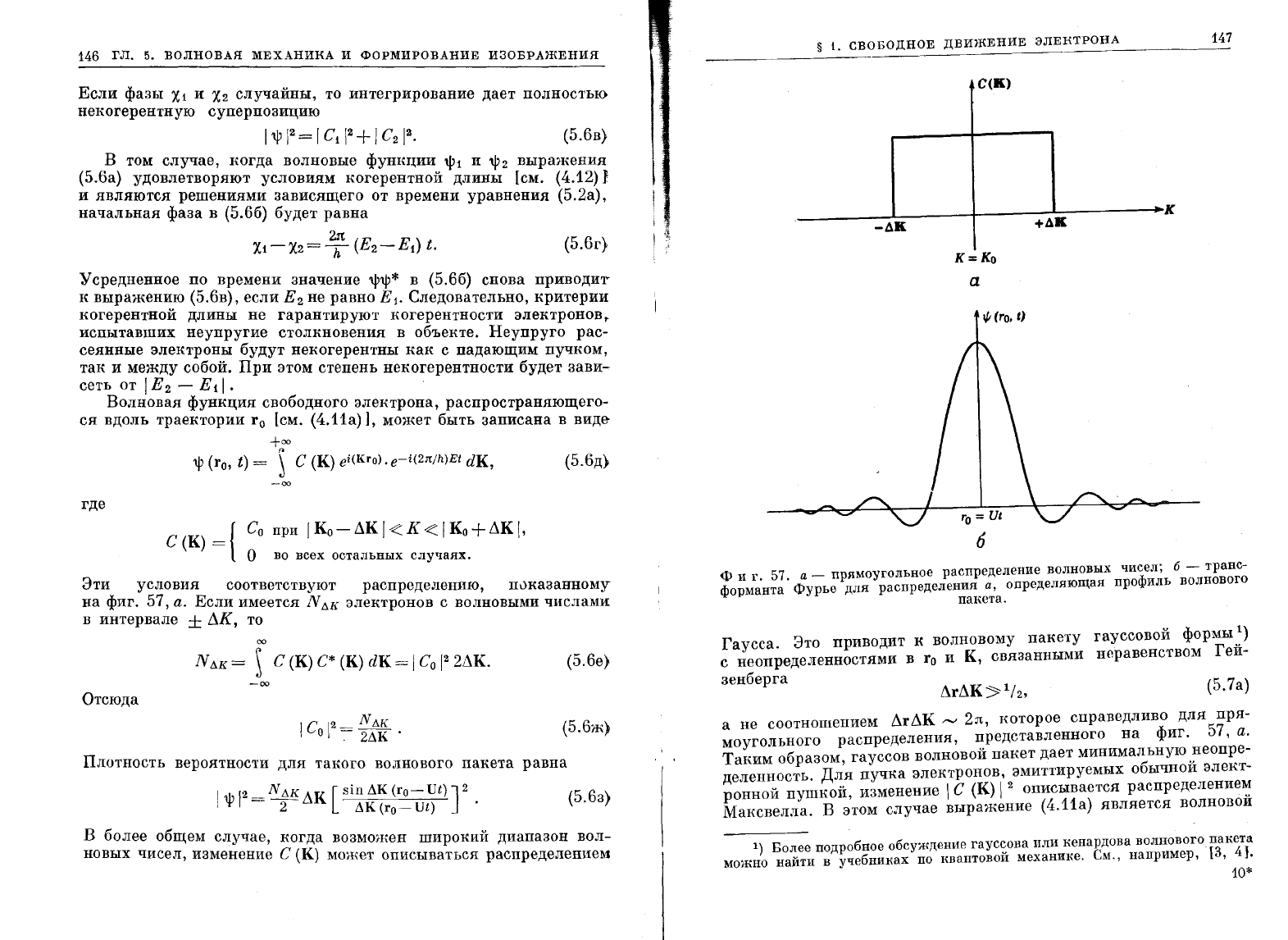
а
ф
(ro,
е)
6
+АК
147
--К
ф
57
а
_
прямоуrольное
распределение
волновых
чисел;
6 -
транс
Фо;:~нта'
Фурье
для
распределения
а,
определяющая
профиль
волновоrо
пакета.
Гаусса.
3то
приводит
к
волновому
панету
гауссовой
формы
1)
В
ro
И
К,
связанными
неравенством
Гей
с
неопределенностями
зенберга
(5.7а)
а
не
соотношением
LlrLlK,-.I
2n,
которое
справедливо
для
пря
моугольного
распределения,
представленного
на
фиг.
57,
а.
Таким
образом,
гауссов
волновой
пакет
дает
минимальную
;rеопре
деленность.
Для
пучка
электронОВ,
эмиттируемых
обычнои
элект
ронной
пушкой,
изменение
I
с
(К)
1 2
описывается
распределение~
Максвелла.
В
этом
случае
выражение
(4.11а)
является
волновои
1)
Более
подробное
обсуждение
гауссова
или
кенардова
волнового
П[:К'4
т
}а
можно
найти
в
учебниках
по
квантовой
механике.
См.,
например,
, .
10*
148
ГЛ.
5.
ВОЛНОВАЯ
МЕХ.А:НИНА
И
~ОРМИРОВАНИЕ
ИЗОБРАЖЕНИЯ
функцией
для
электронов,
и(щускаемых
точечным
источником
с
разбросом
энергии,
равным
~E
..
Поэтому
такой
пучок
электронов
является
только
частично
когерентным.
Конечный
источник
с
~B
,......, 10-4
рад
имеет
значительно
меньшую
когерентную
длину
~x
~
л/2~s,
в
связи
с
чем
контраст
на
интерференционной
кар
тине
обычно
лимитируется
размерами
источника.
Мы
записали
волновую
функцию
в
!Виде
(5.6д),
в
част~ости,
для
того,
чтобы
показать
фурье-обращение:
'
+00
С
(К)
=
2~
~
'ф
(ro,t)
~-i(Кrо)еi(2Л/h)Еt
dro,
-00
+00
(5.7б)
'" (ro, t) =
~
с
(К)
c
i
,(
Kr
o)e-
i
(2Лjh)Еt
dK.
-00
в
этих
взаимных
соотношениях
величины
'Ф
(го,
t)
и
С
(К)
явля
ются
фурье-трансфор.мантu.мu.
Величины
ro
и
К
имеют
обратные
размерности.
В
теории
дифракции
фурье-трансформанты
связы
вают
распределение
амплитуд
В
nря,мо,м
и
обратно,м
пространст
вах.
На
фиг.
57,
б
показан
профиль
волнового
пакета,
соответ
ствующего
прямоугольному
распределению
волновых
чисел
(фиг.
57,
а).
§ 2.
Движение
через
границу
двух
сред
В
§ 1
было
рассмотрено
свободное
движение
электрона,
причем
за
нулевое
приближение
к
истинной волновой
функции
была
при
нята
простая
плоская
волна
С
oei(l(r).
Теперь
мы
рассмотрим
)i;оведение
электр'она,"
переходящего
из
вакуума,
в
KOTOP~M
отсут
ствуют
внешние
поля,
в
среду
с
потенциалом
V
o
•
Для'
этой
цели
достаточно
рассмотреть
монохроматическую
плоскую
волну.
,..
Пу~ть
К
и
будет
волновой
вектор
падаю
шей
BO~HЫ,
К
-
про-
:-Ходящей,
а
К
и
-
щ>лны,
.
отраженной
повер:х:ностью
z =
О.
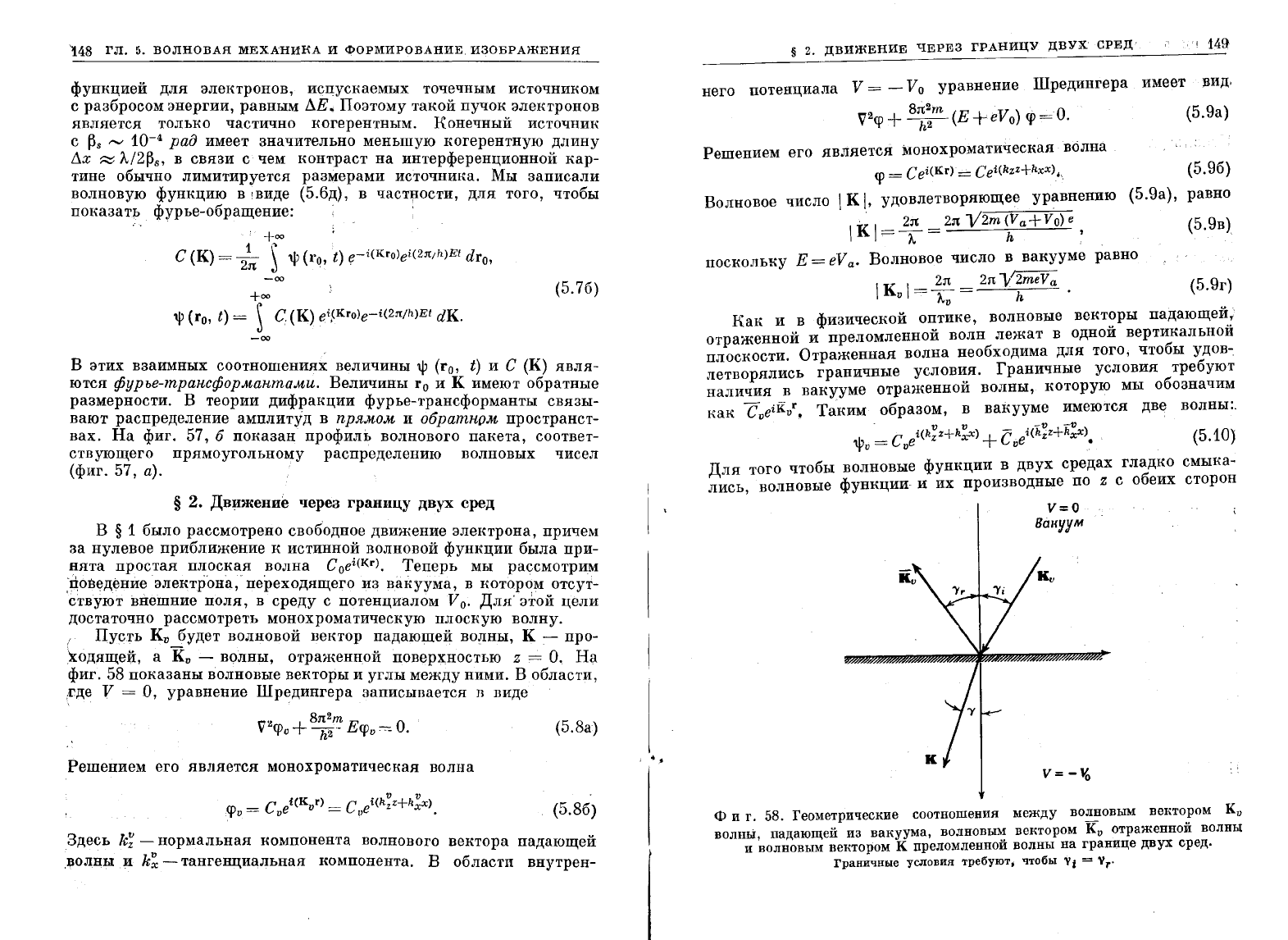
На
фиг.
58
показаны
волновые
векторы
и
углы
между
ними.
Вобласти,
:где
V =
О,
уравнение
Шредингера
ааписывается
в
виде
\
,.
\'72
+8л
2
m
Е
О
v
ери
liJ.'-
epv:-:c-:.
•
(5.8а)
Решением
его
является
монохроматическая
волна
(5.8б)
Здесь
k~
-
нормальная
компонента
волнового
вектора
падающей
,:~ЮЛНЫ
.
и
k~
-
тангенциальная
компонента.
В
области
внутрен-
I •
,_
§ 2.
ДВИЖЕНИЕ
ЧЕРЕЗ
ГРАНИЦ'У
ДВ'УХ'
СРЕД'
,'!
149'
него
потенциала
V = - V
o
уравнение
Шредингера
имеет
~ид,
8л
2
m
'
'о
V
2
ep
+
---w:-
(Е
+ eVo)
ер
=.
(5.9а)
Решением
его
является
монохроматическая
волна
ер
=
Cei(Kr)
~
Cei(kzz+kxx).\
(5.96)
Волновое
число
\
к
\,
удовлетворяющее
уравнению
(5.9а),
равно
;'
2п 2л
V2m(V
a
+Vo)е
(5.9в),
\К\:--Г=
h
~
ПОСКОЛЬRУ
Е
=
eV
a
•
Волновое
число
в
вакууме
равно
\
К
I
-,
~
- 2n
-yъnev;;
(5.9г)
v -
Л
V
- h •
Как
и
в
физической
оптике,
волновые
BeKT~pы
падающей}
отраженной
и
преломленной
волн
лежат
воднои
вертикальнои
плоскости.
Отраженная
волна
необходима
для
того;
чтобы
удов-,
летворялись
граничные
условия.
Граничные
условия
требуют
наличия
в
вакууме
отраженной
волны,
которую
мы
обозначим
как
C~eiKvr.
Т~ким
образом,
в
вакууме
имеются
две
волны:.
- v v .
-v -v
_
с·
i(k
z
z+kxx)
+
С-
.
e~(kiZ+kxX).
(5.1
О)
'Фv
- v
e
v
.'
Для
того
чтобы
волновые
функции
в
двух
средах
гладко смыка
лись,
волновые
функции-
и
их
производные
по
z
с
обеих
сторон
v=o
вакуум
V=-'Ь
Фиг.
58.
Геометрические
соотношения
между
волновым
вектором
K
v
волны
падающей
из
вакуума,
волновым
вектором
K
v
отраженнои
волны
и
~олновым
вектором
К
преломленной
волны
на
грающе
двух
сред.
Граничные
условия
требуют;
чтобы
"1 =
"r'

15Ь
ГЛ.
5.
ВОЛНОВАЯ
МЕХАНИRА
И
ФОРМИРОВАНИЕ
ИЗОБРАЖЕНИЯ
от
поверхности
были
равны
'l'v:(
z =
О).
=
'1'
(z
=
О),
a~v
/z=o
=
-~~
/z=o
.
(5.11а)
Используя
выражения
(5.10)
и
(5.9б),
получаем
eveik~x
=
Cveik~X
+ Ceikxx,
k
V
С
eik~x
-
-kvС-
ik~x
+ k
ik
х
z
v-
z
ve
ze
х
•
(5.11б)
Эти
соотношения
справедливы
для
всех
значений
х.
Последнее
означает,
что
все
~Rспоненты
равны,
или
(5.11в)
с
другой
стороны,
на
границе
двух
сред
тангенциальные
компо
ненты
всех
волновых
векторов
должны
быть
равны.
Если
'Yi
_
угол падения,
Yr
-
угол
отражения
и
)' -
угол
преломления,
то это
условие
записывается
в
виде
I K
v
I
sin
Yi
= I K
v
I sin)'1' = I
к
I
sin)'.
Так
как
I
к
I = I K
v
I ,
то
sin
)'i
=
sin
)'1"
т.
е.
угол
падения
равен
углу
отражения
.•
Таким
образом,
закон
Снелля
для
электронов
может
быть.
записан
в
виде
sin
Yi
К
sin
У
= K
v
=~,
(5.11г)
где
,.,.,
-
показатель
преломления.
Используя
(5.9в)
и
(5.9г),
получаем
11'=V~,",,1+~
r V
а
'""
2V
а
'
(5.11д)
так
как
для
жестких
'электронов
V
a
~
V
o
•
Отсюда
видно,
что
показа
тель
преломления
больше
единицы,
и
поэтому
групповая
скорость
в
среде
с
неравным
нулю
внутренним
потенциалом
боль
ше,
чем
в
вакууме.
Если
учесть
условие
равенства
тангенциальных
компонент
волновых
векторов
на
границе
(5.11в),
то
выражения
(5.11б)
принимают
вид
Cv=Cv+C,
k~Cv
=
k~Cv
+ kzC.
Из
(5.12а)
можно
получить
отношение
амплитуд
С
2 I K
v
I cos
У
i 2
С
v
=:=
I K
v
I COS
Yi
+ I
к
I COS
У
~
f.t
+ 1 '
c~
_IKlcosY-IКv!соsУi
С
р
- I K
v
I cos
у
i + I
к
I cos
У
f.t-1
~--
~+1
(5.12а)
(
5.12б)
;"
§
З.
ПРОХОЖДЕНИЕ
ЭЛЕRТРОНОВ
ЧЕРЕЗ
ТОНRИЙ
СЛОЙ
151
для
случая,
когда
направление
падения
близко
к
нормальному,
т.
е.
когда
)'i
И
)'
малы.
Коэффициент
отражения
на
границе
равен
отношению
отражен
ного
потока
к
падающему.
Плотность
падающего
потока
электро
нов
равна
J =
hK
v
I
С
12
v
2л:m
v,
так
как
hК
v
/2л:m
-
скорость,
I C
v
12
-
плотность
частиц.
Таким
образом,
коэффициент
отражения
будет
равен
J
v
\ C
v
12
(5.12в)
1;=
1 C
v
12
'
а
коэффициент
прохождения
-
J 1
к
1 1
С
12
1
С
\2
1;
=
тк;r
I C
v
12
=
~
1 C
v
12
•
Величина
V
o
обычно
имеет
порядок
15
эв,
так что
при
Е
=
105
показатель
преломления
очень
мал
(,.,.,
- 1
~
7 ·10-0).
Коэффи
циент
отражения
при
нормальном
падении
по
порядку
величины
равен
10-10,
т.
е.
совершенно
не
значителен
1).
Поэтому
для
всех
практических
задач
амплитуды
падающей
и
прошедшей
волн
равны.
Результат
мало
меняется,
I\aK
это
было
показано
Лауэ
[5],
если
предположить,
что
потенциал вблизи
поверхности
z =
О
изменяется
экспоненциально.
§
3.
Прохождение
электронов
через
тонкий
слой
с
внутренним
потенциалом,
отличным
от
нуля
Если
ограничить
область
с
внутренним
потенциалом
V
о
вто
рой
плоскостью
(поверхностью
выхода),
получим
пленку
с
внут
ренним
потенциалом
V
о
и
толщиной
t.
Вследствие
того
что
коэф
фициент
отражения
пренебрежимо
мал,
амплитуды
падающей
и
вышедшей
волн
будут
практически
одинаковыми.
Если
же
учи
тывается
упругое
и
неупругое
рассеяние,
то
такое
предположение
будет
неверным.
Но
мы
пока
что
пренебрежем
затуханием
падаю
щего
аксиального
пучка
и
будем
считать,
что
пучок
падает
нор
мально
к
поверхности.
Рассмотрим
волну,
данную
выражением
(5.9б)
в
пленке
с
внут
ренним
потенциалом
V
o
и примем,
что
k
x
=
О.
Тогда
волновая
функция
на
поверхности
выхода
может
быть
записана
в
виде
Ce
iki
=
Ce
iKt
=
С
ехр
i
2:
t
V2m
(V
a
+ V
o
)
е.
(5.13а)
1)
Следует
отличать
данный
случай
от
случая
рассеяния
вторичных
электронов
в
направлении,
обратном
по
отношению
к
падающему
пуч
ку
(гл.
12).
152
ГЛ.
5.
ВОЛНОВАЯ
МЕХАНИНА
И
ФОРМИРОВАНИЕ
ИЗОБРАЖЕНИЯ
в
отсутствие
пленки
волновая
фУНКЦИЯ
равна
С
iK
t
С
.
2л
У2
V
е
v =
ехр
~
h t
те
а'
(5.13б)
ИЗ
этих
соотношений
видно,
что
амплитуды
обеих
волн
одина
...
ковы.
Таким
образом,
в
первом
приближении
волновые
функции
отличаются
друг
от
друга
только
фазой.
Для
z>
t
волновая
функци~
<<Вышедшей»
волны
может
быть
записана
в
виде
z>1,
(5.13в)
где
I К
1
1
= I
К
и
!.
На
границе
(z
= t)
волновые
функции
<<внутрен
ней»
и
<<Вышедшей»
волн
должны
удовлетворять
граничным
УСЛОВИЯМ,
что
дает
или
<Р1
=
<р,
C1eiKlt
=
Ce
iKt
,
(5.13г)
Используя
выражения
(5.9в)
и
(5.9г)
для
К
и
К
1
,
получаем
I
К-К
1
1
=
2:
(У2т
(1/а
+ V
o
)
е-
V2meV
a
)
~
I
К
I
УО
лV
о
~
1
2У
а
=
ЛV
а
•
(5.13д)
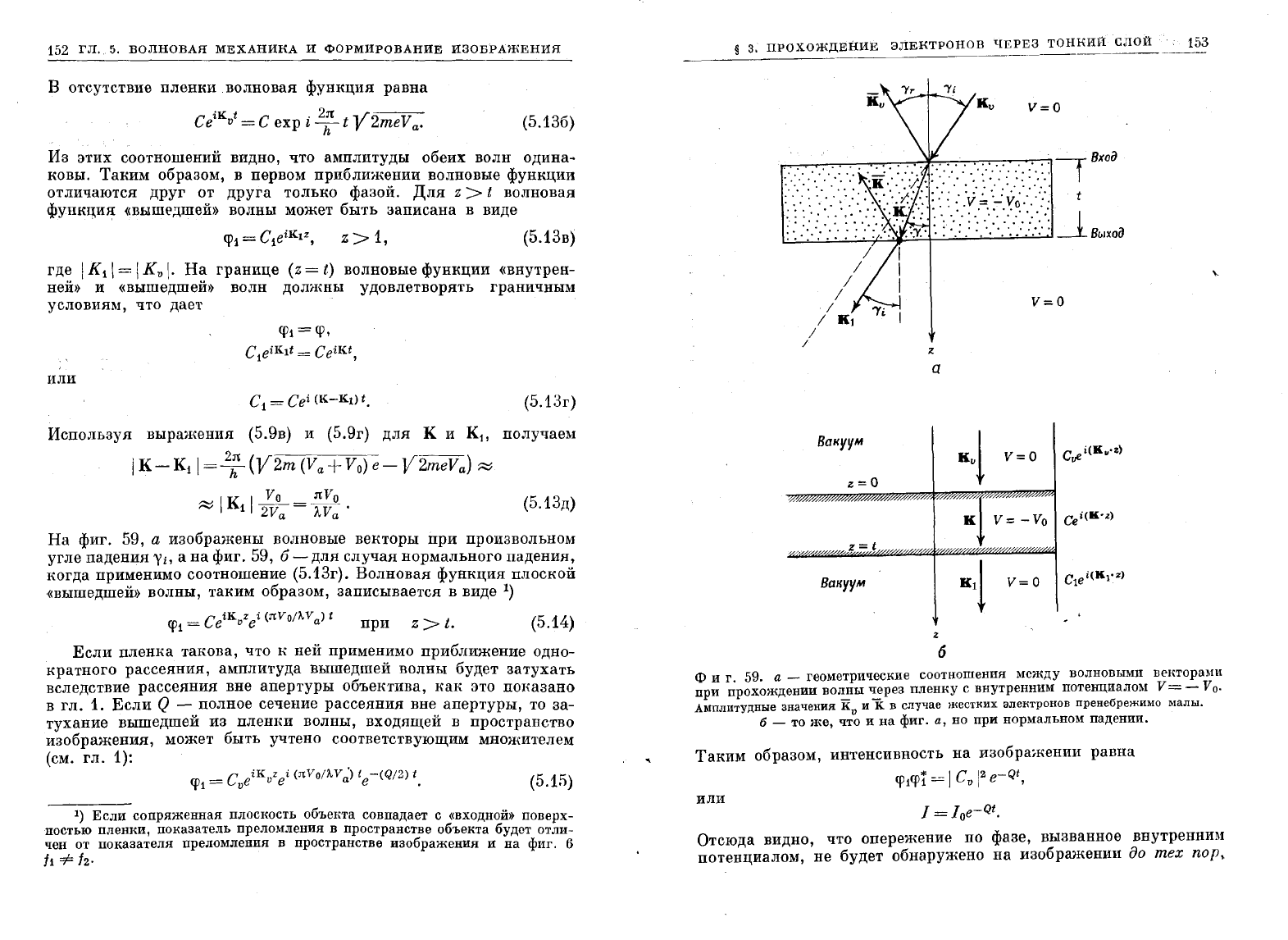
На
фиг.
59,
а
изображены
волновые
вен
торы
при
произвольном
угле
падения
'Vi,
а
на
фиг.
59,
б
-
для
случая
нормального
падения,
ногда
применимо
соотношение
(5.13г).
Волновая
фуннция
плосной
<<Вышедшей»
волны,
таним
образом,
записывается
в
виде
1)
при
z>t.
(5.14)
Если
пленна
танова,
что
н
ней
применимо
приближение
одно
кратного
рассеяния,
амплитуда
вышедшей
волны
будет
затухать
вследствие
рассеяния
вне
апертуры
объектива,
как
это
показано
в
гл.
1.
Если
Q -
полное
сечение
рассеяния
вне
апертуры,
то
за
тухание
вышедшей
из
пленки
волны,
входящей
в
пространство
изображения,
может
быть
учтено
соответствующим
множителем
(см.
гл.
1):
_
с
eiKvzei
(JtVo/~
V
d>
t
-(Q/2)
t
С:Р1-
v
е.
(5.15)
1)
Если
сопряженная
плоскость
объекта
совпадает
с
<<Входной»
поверх
ностью
пленки,
показатель
преломления
в
пространстве
объекта
будет отли
чен
от
показателя
преломления
в
пространстве
изображения
и
на
фиг.
6
11
=1=
12'
а
z;=o
И'l
у=о
Cvei(KI/'z)
Вакуум
К
у=
-уо
Cei(K.z)
~
у/////.о
Z - t
'"
'Н-
вакуум
и'l
у=о
Cl
e
i(K
1
·z)
z
б
ф
и
г.
59.
а
-
геометрические
соотношения
между
волновыми
векторами
при
прохождении
волны
через
пленку
с
внутренним
потенциалом
V = - V
o
•
Амплитудные
значения
К
и
и
к
в
случае
жесткИХ
электронов
пренебрежимо
малы.
б
-
то
же,
что
и
на
фиг.
а,
но
при
нормальном
падении.
Таким
образом,
интенсивность
на
изобрашении
равна
С:Р1С:Р'1
= I
С
и
12
e-
Qt
,
или
/ =
/oe-
Qt
•
Отсюда
видно, что
опережение
по
фазе,
вызванное
внутренним
потенциалом,
не
будет
обнаружено
на
изображении
до
тех
nop~
154
гл.
5.
ВОЛНОВАЯ
МЕХАНИКА
И
ФОРМИРОВАНИЕ
ИЗОБРАЖЕНИЯ
no~a
волна
(5.15)
не
соединится
с
падающей
волной.
Только
при
этом
условии
разность
фаз
дает
интерференционную
картину
на
изображении,
так
как
суммарная
волна
в
этом
случае
будет
иметь
вид
'Ф
=
(})1
+
(})v
=
С
veiKvz
(1
+ e
i
(nVо/л
v
а)
е.
е
-(Q/2)
t),
(5.16а)
д
интенсивность
'Ф'Ф*
= 1 C
v
12
( 1 +
e-
Qt
+
2e-(Q/2)
t cos
~
~:
t ) .
(5.16б)
Оптическая
система,
в
которой
используются
два
когерентных
пучка
с
контролируемой
разностью
фаз
и
наблюдается
интерфе
ренционная
картина,
называется
uuтерфереUЦUОJ-U-lЬLJtf,
Mи~poc~o
ЛОМ.
Соотношение
(5.16б)
описывает
интенсивность
изображения,
полученного
в
интерференционном
микроскопе.
Оно
является
также
основным
в
электронной
фазовой
микроскопии,
в
:которой
увеличение
контраста
достигается
путем
изменения
разности
фаЗе
До
сих
пор
мы
рассматривали
влияние
только
среднего
внут
реннего
потенциала
V
o
,
который
на
самом
деле
является
лишь
первым
членом
в
фурье-разложении
потенциала
в
:кристалле
(см.
гл.
7, § 3).
Периодические
члены
потенциала
ответственны
за
электронную
дифракцию,
и,
как
можно
видеть
из
выражения
(5.16б),
если
V
o
в
пленке
будет
иметь
периодический
характер,
изменения
фазы
будут
также
периодическими.
Если
пренебречь
экспонентой
e-
Qt
,
ответственной
за
затухание,
то
периодический
потенциал
в
пленке
представляет
собой
электронную
фазовую
решетку.
Поскольку
потенциал
в
основном
модулирует
фазы,
а
не
амплитуды,
результирующее
распределение
интенсивности,
или
контраст,
на
изображении
обусловлено
изменениями
именно
фазы.
Очень
тонкий
кристалл
толщиной
~Z
на
основании
(5.13д)
будет
давать
изменение
фазы
лV
I
К-
К
1
1
~Z
=
ЛV
а
~z.
(5.17а)
Волновая
функция
<<Вышедшей»волны
(5.15)
в
этом
случае
равна
(})1
=
CveiKvZei
(nV/лV
а
)
6.Z
e
-(Q/2)
6.z
~
С
iK
Z
(1
Q
А
•
лV
А
)
~
v
e
v
-ТLlZ+
~
ЛV
а
LlZ.
(5.17б)
Это
выражение
послужило
отправной
точкой
для
анализа
рассея
ния,
проведенного
Rаули
и
Муди
[6],
:которые
рассматривали
фазовую
решетку
с
учетом
изменения
амплитуды.
§ 4.
Электронные
интерференционные
микроскопы
Первым,
кто
серьезно
рассмотрел
проблему
конструирования
электронного
интерферометра,
был,
по-видимому,
Мартон
[7].
Вместе
с
Симпсоном
и
Садетом
[8]
он
установил
последовательно
§ 4.
ЭЛЕКТРОННЫЕ
ИНТЕРФЕРЕНЦИОННЫЕ
МИКРОСКОПЫ
155
'Три
монокристаллические
пленки
для
получения
расщепленных
пучков
и
последующей
их
рекомбинации
с
образованием
интерфе
ренционной
картины.
Интерферомежр
такого
типа
дa~T
слабые
интерференционные
контуры.
Вскоре
после
этого
Меленштедт
и
Дюкер
[9]
получили
интерференционную
картину
с
помощью
:электронной
бипризмы.
В
качестве
бипризмы
использовалась
кварцевая
нить
диаметром
2
M~,
покрытая
металлом
и
установлен
ная
так,
как
показано
на
фиг.
60.
Для
расщепления
падающего
пучка
и
последующего
соединения
пучков
к
нити
прикладывалось
напряжение
в
несколькО
вольт.,
u
Плоскость
Z = L
на
фиг.
60
является
сопряженнои
плоскостью
объекта
объективной
линзы,
которая
необходима
для
увеличения
-:-
z =
L---
L....-..J......:..-~
..........
--'
----i
...
~x
1
z
Фиг.
60.
Схема
электронно-оптической
бипризмы
Френеля.
80 -
источник
электронов
[9].
F _
металлизированная
нварцевая
нить
ТОЛЩИНОЙ
оноло
2
.мn.
81
и
82 -
два
Hoг~peHT
ных
виртуальных
источнина.
Интерференционная
нартина
наблюдается
в
о
ластИ
.
перенрытия
ПУЧНОВ.
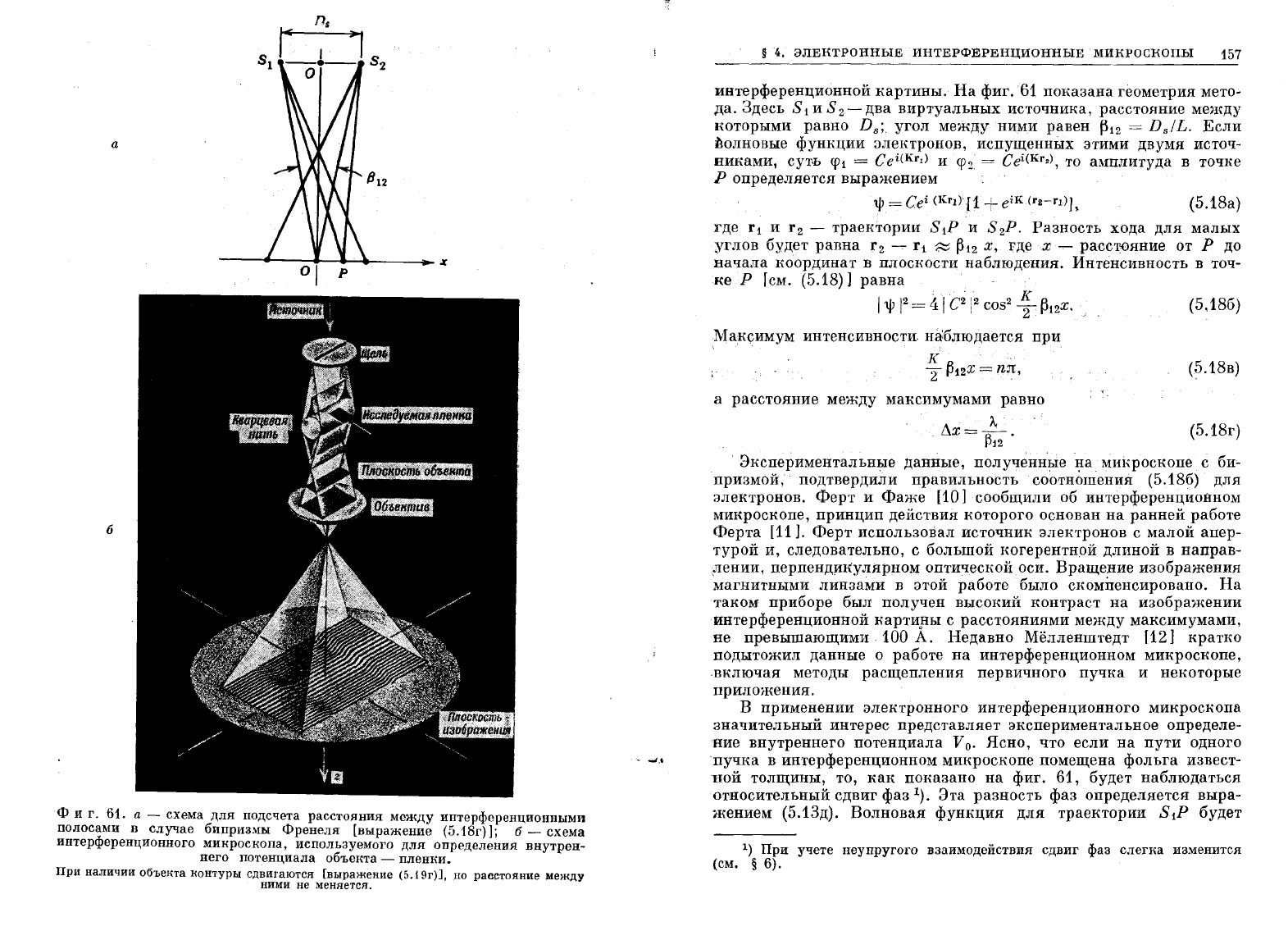
а
6
ф
и
г.
61.
а
-
схема
для
подсчета
расстояния
между
интерференционными
полосами
в
случае
бипризмы
Френеля
[выражение
(5.18г)];
б
-
схема
интерференционного
микроскопа,
используемого
для
определения
внутрен-
него
потенциала
объекта
-
пленки.
При
наличии
объеита
I\ОНТУРЫ
сдвигаются
[выражение
(5.19r)J,
но
расстояние
между
ними
не меняется.
.......
§4.
ЭЛЕКТРОННЫЕ
ИНТЕРФЕРЕНЦИОННЫЕ'
МИКРОСRОПЫ
157
интерференционной
картины.
На
фиг.
i61
ПОRазана
геометрия
мето.;.
да.
Здесь
S 1
и
S 2 -
два
виртуальных
ИСТОЧНИRа,
расстояние
мещду
которыми
равно
D
s
;
угол
между
ними
равен
~12
= Ds/L.
Если
))олновые
функции
элеRТРОНОВ,
испущенных
этими
двумя
источ
никами,
сут.ь
ер1
=
СеН
КГ
l)
иерz,
=
Сеi(КГ
г
),
то
амплитуда
в
точке
р
определяется
выражением
'Ф=
Ce
i
(Kr
1
)'{1 + e
iK
(Г
2
-
n
)1,
(5.18а)
тде
r 1
и
r 2 -
траектории
S
l
Р
и
S
2
Р
'
Разность
хода
для
малых
углов
будет
равна
r2
~
rl
~
~12
Х,
гд~x
-,-
расст;ояние
от
Р
до
начала координат
в
ПЛОСRОСТИ
наблюдения.
Интенсивность
в
точ
пеР
[см.
(5.18)]
равна
, '
к
I'Ф
12
=
41
С
2
1
2
cos
2
Т
~12X'
'
(5,18б)
,Ма:к~имум
интенсивности,
наблюдается
при
к
'"
z
В12
Х
=
n1!'
а
расстояние
между
максимумами
равно
,
л
,
ДХ=-г
JJ12
(?18в)
(5.18г)
,
Экспериментальные
Данные,
полученные
на
микроскопе.
с
би'
призмой,'
подтвердили
правильность
соотнЬшенил
(5.18б)
для
электронов.
Ферт
и
Фаже
[10 1
сообщили
об
интерференционном
МИRроскопе,
принцип
действия
которого
основан на
ранней
работе
Ферта
[111.
Ферт
ИСПОЛЬЗ0вал
ИСТОЧНИR
элеRТРОНОВ
с
малой
апер
турой
и,
следовательно,
с
большой
Rогерентной
длиной
в
направ
,?'!ении,
перпеНД~RУЛЯРНОМ
оптичеСRОЙОСИ.
Враще:ние
изображения
магнитными
линзами
в
этой
работе
было
скомпенсировано.
На
таном
приборе
был
получен
ВЫСОRийконтраст
на
изображении
йнтерференционной
RаРТИ}IЫ
с
расстояниями
между
маRсимумами,
не
превышающими,
100
А.
Недавно
Мёлленштедт
[12]
кратко
подытожил
данные
о
работе
на
интерференционном
микроскопе,
,включая
методы
расщепления
первичного
пучка
и неноторые
приложения.
В
применении
элеRТРОННОГО
интерференционного
МИКРОСRопа
значительный
интерес
представляет
ЭRспериментальное
определе
'яие
внутреннего
потенциала
V
o
•
Ясно,
что
если
на
пути
одного
'пучка
винтерференционном
МИКРОСRопе
помещена
фольга
извест
'ной
толщины,
то,
как
ПОRазано
на
фиг.
61,
будет
наблюдаться
относительный
сдвиг
фаз
1).
Эта
разность
фаз
определяется
выра
жением
(5.13д).
Волновая
функция
для
траектории
Sl
P
будет
1)
При
учете
неупругого
взаимодействия
сдвиг
фаз
слегка
изменится
(см.
§ 6).

158
ГЛ.
5.
ВОЛНОВАЯ
МЕХАНИНА
И
ФОРМИРОВАНИЕ
ИЗОБРАЖЕНИЯ
той
же
самой
ер!
=
Cei(Kr
t
),
но
для
траектории
S
2
Р
она
примет
вид
если
использовать
выражение
(5.15)
и
пренебречь
затуханием
за
счет
рассеяния.
Интенсивность
в
точке
Р
будет
равна
11P12=4ICI2COs2
~
(K~12X+
~;:
t).
(5.19а)
Первый
максимум
смещен
по
отношению
к
х
=
О
на
расстояние
Х1=
Второй
максимум
будет
при
Х2=_1-
(.!_~
t)
~12
л.
2V
а
.
(5.19б)
(5.19в)
Нак
легко
показать,
расстояние
между
этими
двумя
максимумами
остается
прежним:
л.
АХ=Х2-
Х
l
=
-,
~12
но
максимумы
сдвигаются
на величину,
определяемую
(5.19б).
Определяя
~12
из
выраженкя
(5.18г),
можно
записать
это
рас
стояние
в
виде
или
(5.19г)
если
использовать
данные
табл.
20
приложения
VII.
На
основе
соотноuшения
(5.19г)
Бул
[13]
экспериментально
определил
внут
реннии
потенциал
ряда
материалов.
На
фиг.
62
показана
ин
тер
ференционная
нартина,
обусловленная
сдвигом
фазы при
прохож
дении
электронов
сквозь
алюминиевый
диск
толщиной
230
А
лежащий
на
алюминиевой
подложке.
По
такой
МИКРОфотографИ~
можно
определить
Ах
и
Хl
для
диска.
Значения
V
o
,
полученные
таким
образом,
приведены
в
табл.
51).
Точность
приведенных
значений
определяется
в
основном
точностью
измерения
расстояния
между
полосами
и
толщины
образца.
Ферт
И
Фаже
[10]
получили
для
монокристал.ча
графита
V
o
=
11
эв,
предполагая,
что
напыленный
углерод
значительно
менее
плотно
упакован,
чем
графит.
Полученные
таким
образом
1)
Некоторые
значения
среднего
внутреннего
потенциала
даны
в
таб.lI.
1&
(приложение
III).
§ 4.
ЭЛЕНТРОННЫЕ
ИНТЕРФЕРЕНЦИОННЫЕ
МИНРОСНОПЫ
159
значения
внутреннего
потенциала,
вероятно, не
более
чем
на
2-
3
эв
отличаются
от
истинных
значений.
Оприменении
интерферен
ционного
микроскопа
при
исследовании
ряда
других
материалов
говорится
в
работе
[15].
Таким
образом,
мы
видим,
что
разработка
интерференционного
микроскопа
явилась
практическим
достижением,
основанным
Таблица
5
Значения
среднего
внутреннего
потенциала
V
o
,
определенные
при
помощи
электронного
интерференционного
микроскопа
1)
(45-50
"в)
[13,
14]
Материал
с
(напыленный)
Al
Си
Ag
Аи
уо,
эв
7,8±0,6
13,0±0,4
23,5±0,6
17-22
22-27
1)
Неиоторые
значения
среднего
,тутреннего
потен
циала
даны
в
табл.
18
(приложение
III).
на
правильном
понимании
тех
фазовых
изменений,
которыми
сопро
вождается
прохождение
электронов
через
объект.
В
1949
г.
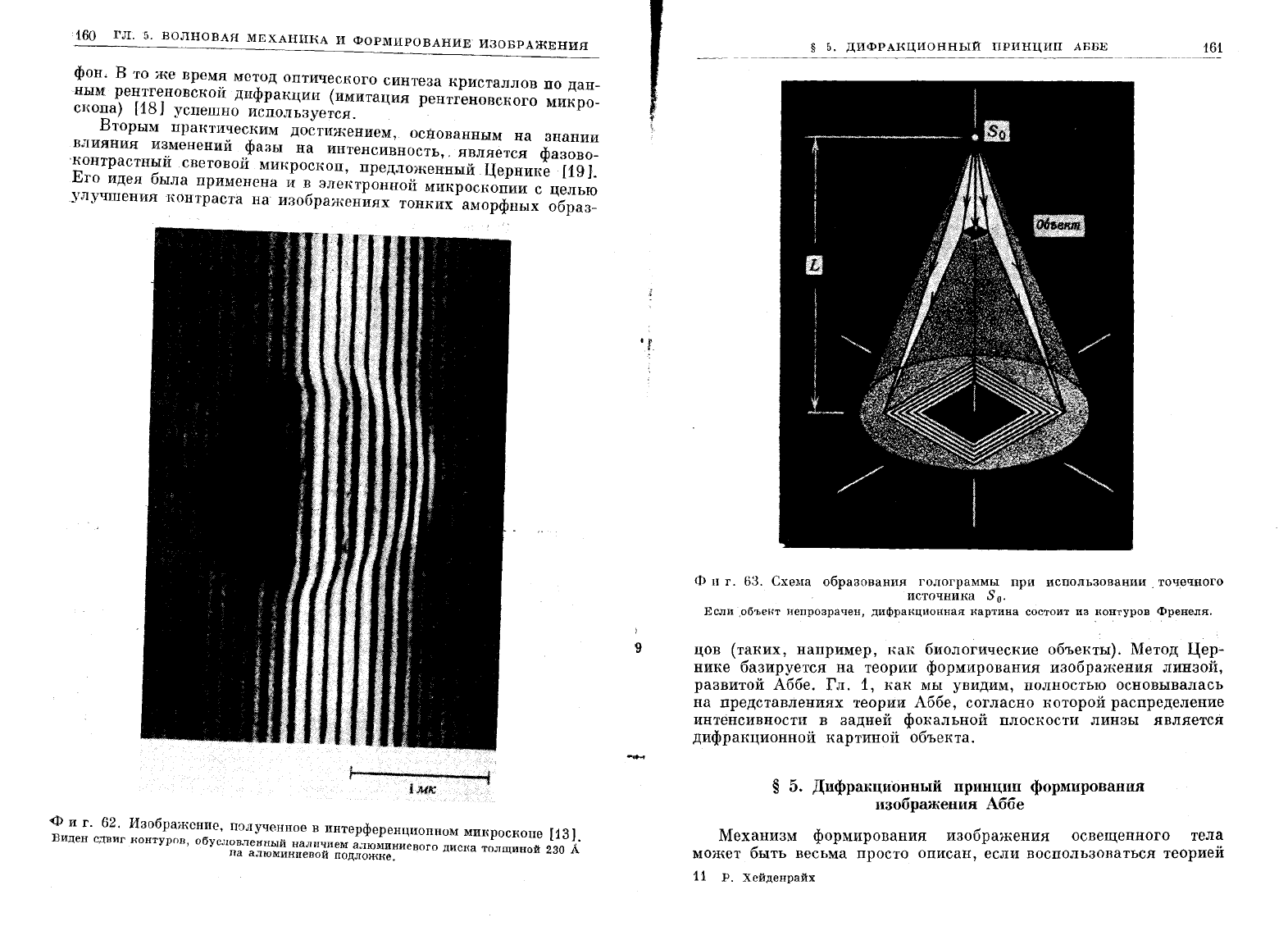
Габор
[16]
предложил
использовать
в
интерферен
ционной
микроскопии
метод
реконструкции
волновых
фронтов~
В
этом
методе
точечным
источником
освещается
объект
с
произ-
вольным
распределением
толщин,
которое
вызывает
изменение·
фаз
выходящих
волн.
Геометрия
метода
показана на
фиг.
63.
На
экране,
расположенном
на
расстоянии
L
от
источника,
реги
стрируется
изменение
фазы
как
распределение
интенсивности
в
интерференционной
картине,
называемой
голограммой.
Голо
грамма
данного
объекта
воспроизводится
на
прозрачном
экране
и
помещается
в
исходное
положение.
Если
теперь
смотреть
на
нее
в
направлении
источника
при
устраненном
объекте,
то
снова
<<ВИ
дею>,
объект,
воссозданный
интерференционной
картиной.
Хотя
Хэйну
и
Малви
[17]
и
удалось
получить
таким
путем
изображение,
метод,
вероятно,
нецелесообразен
в
случае
применения
электро
нов.
Во-первых,
ограниченная
поперечная
когерентная
длина
не
позволяет
получить
достаточно
большую
голограмму
и,
во
вторых,
некогерентное
рассеяние
увеличивает
нежелательный,
160
ГЛ.
5.
ВОЛНОВАН
МЕХАНИКА
И
ФОРМИРОВАНИЕ
ИЗОБРАЖЕНИЯ
фон.
В
то
же
время
метод
оптического
синтеза
кристаллов
по
дан
ным
рентгеНОВСRОЙ
дифракции
(имитация
рентгеновсного
микро
скопа)
[181
успешно
используется.
Вторым
праRтическим
достижением,
осцованным
на
знании
влияния
и~менений
.~азы
на
интенсивность"
является
фазово
'контрастныисветовои
МИКРОСI\ОП,
предложенный
ЦеРНИI\е
(19
J.
Его
идея
была
применена
и
в
электронной
микроскопии
с
целью
улучшения
'Контраста
на
изображениях
тОнких
аморфных
образ-
~
и
г.
62.
Изображение,
полученное
винтерференционном
МИI{роскопе
[13J.
Виден
сдвиг
контурnв,
оБУСJlOВ.'IенныЙ
налИчием
алюминиевnго
диска
толщиной
230
А
па
алюминиевой
ПОДложке.
§ 5.
ДИФРАИЦИОННЫЙ
ПРИНЦИП
АББЕ
161
ф
II
г.
63.
Схема
образования
голограммы
при
использовании,
точечного
источника
S
о.
Если
,объект
непрозрачен,
дифракционная
картина
состоит
из
контуров
Френеля.
, ,
9
цов
(таких,
например,
!{ак
биологические
объекты).
Метод
Цер;..
нике
базируется
на теории
формирования
изображения
линзои,
развитой
Аббе.
Гл.
1,
как
мы
увидим,
полностью
основывалась
на
представлениях
теории
Аббе,
согласно
RОТОРОЙ
распределение
интенсивности
в
задней
фОRальной
ПЛОСRОСТИ
линзы
является
дифраRЦИОННОЙ
картиной
объекта.
-
.....
§ 5.
Дифракци'онный
принцип
формирования
и:зображенин
Аббе
Механизм
формирования
изображения
освещенного
тел~
может
быть
весьма
просто
описан,
если
воспользоваться
теориеи
11
Р.
Хсйденрайх
