Холоднов В.А. Системный анализ и принятие решений. Компьютерное моделирование и оптимизация объектов химической технологии в MathCad и Excel
Подождите немного. Документ загружается.


111
k1 p t( ) exp 32.418
0.149 p 1000( ) 15416
t 273
k2 p t( ) exp 48.324
0.095 p 1000( ) 23678
t 273
Given
1
tau
xa k1 p t( ) ro ga0
0.5
gO0
0.5
1 xa( )
1.5
1 xk( )
0.5
0
1
tau
xk k2 p t( ) ro 1 xa( ) 1 xk( ) ga0
0
va 1995.85 601.21 log
p
1000
593.31 log
1
T
335.8 log
P
1000
log
1
T
1
0
vp 1.152 10
3
7 10
7
T 273.15( ) 5.3 10
8
p
0
v2 va vp
0
v2 va gO0 1 xk( ) v2
0
ro v1 ga0 1 xa( ) v2[ ]
1
0
a5 t
2
t5
2
a2 a4 p( ) t t5( ) Kw F
t 20
G
ga0 xa 1.05 718.6 0.05 t 0.025 p( )
0
xa
0.2
xk
0.6
t 240
va
0
vp
0
v2
0
v1
0
xa
xk
va
vp
v2
v1
ro
t
Minerr xa xk va vp v2 v1 ro t( )
xa
xk
va
vp
v2
v1
ro
t
0.241
1
2.287 10
3
1.261 10
3
1.026 10
3
2.287 10
3
326.932
324.125

112
6.2 Моделирование процессов на основе решения дифференциальных
уравнений
6.2.1 Моделирование нестационарного химического процесса, протекающего
в реакторе непрерывного действия с мешалкой при изотермических
условиях
Рассмотрим моделирование нестационарного химического процесса
EDA2,DB2A
, протекающего в реакторе непрерывного действия с
мешалкой в изотермических условиях. Задан объём реактора и объёмный расход
подачи исходной смеси, известны кинетические параметры процесса.
Математическое описание процесса имеет вид системы дифференциальных
уравнений:
Re)eebx(
tau
1
dt
de
Rd)ddbx(
tau
1
dt
dd
Rb)bbbx(
tau
1
dt
db
Ra)aabx(
tau
1
dt
da
Известны начальные и граничные условия. Скорости реакций определяются по
формулам:
dak2bakra
2
2
2
1
,
2
1
bak2rb
dak2bakrd
2
2
2
1
,
dakre
2
2
Далее представлен текст программы для моделирования данного процесса в
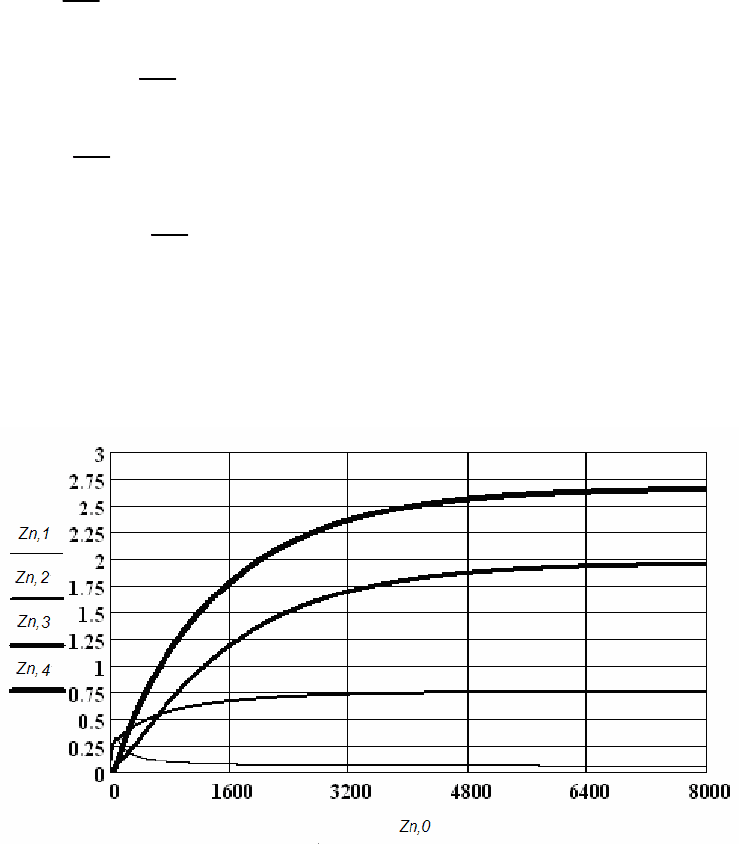
пакете программ Mathcad. На рисунке 6.2 представлены результаты
моделирования – графики изменения концентраций веществ в реакторе во
времени.
Изучение нестационарного процесса в реакторе с мешалкой
abx 10
bbx 10
dbx
0
ebx
0
V
5
w
0.2
60
a0
0
b0
0
d0
0
e0
0
k1
0.1
k2
0.3
tau
V
w
tau 1.5 10
3
x
a0
b0
d0
e0
113
Рисунок 6.2 – Результаты моделирования
Динамика
D t x( )
1
tau
abx x
0
k1 x
0
x
1
2
2 k2 x
0
2
x
2
1
tau
bbx x
1
2 k1 x
0
x
1
2
1
tau
dbx x
2
k1 x
0
x
1
2
k2 x
0
2
x
2
1
tau
ebx x
3
k2 x
0
2
x
2
n 0 1000
Z rkfixed x 0 8000 1000 D( )
114
6.2.2 Моделирование нестационарного процесса сульфирования
нафталина в проточном реакторе с мешалкой
В реакторе с мешалкой непрерывного действия в изотермических
нестационарных условиях проводится процесс сульфирования нафталина
серной кислотой:
115
DS DS
SNOH OHSN SNOH OHSN
6k5k
4k
22
3k2k
22
1k
Здесь N – нафталин, S – сульфирующий агент, α – сульфокислота нафталина,
β – сульфокислота нафталина, D – дисульфокислоты нафталина, W – вода (их
концентрации обозначены соответствующими буквами).
Математическое описание процесса в этом случае имеет следующий вид:
2
6
2
54
2
32
2
1
2
6
2
5
2
64
2
3
2
52
2
1
2
6
2
54
2
32
2
1
4
2
32
2
1
W
β
k
W
α
kWβk
W
N
kWαk
W
N
k)SSbx(
τ
1
dt
dS
W
β
k
W
α
k)DDbx(
τ
1
dt
dD
W
β
kWβk
W
N
k)βbxβ(
τ
1
dt
βd
W
α
kWαk
W
N
k)αbxα(
τ
1
dt
αd
W
β
k
W
α
kWβk
W
N
kWαk
W
N
k)WWbx(
τ
1
dt
dW
Wβk
W
N
kWαk
W
N
k)NNbx(
τ
1
dt
dN
Известны начальные и граничные условия.
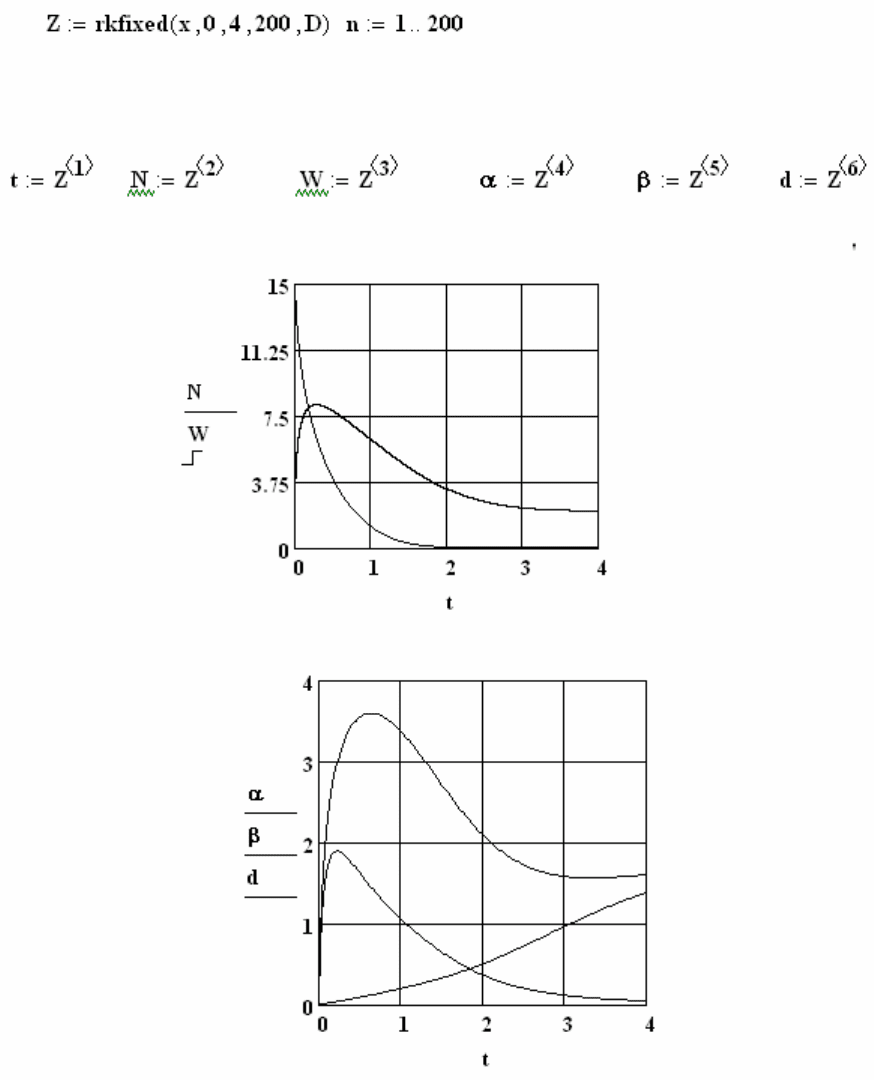
Ниже приведен протокол моделирования этого процесса, а на рисунке 6.3
показаны результаты.

116
117
Рисунок 6.3 – Изменение концентраций соответствующих веществ во времени
для процесса сульфирования нафталина серной кислотой
6.2.3 Моделирование стационарного процесса химического превращения в
трубчатом реакторе в изотермических условиях
Рассмотрим моделирование и расчет трубчатого реактора, в котором в
изотермических стационарных условиях происходит реакция по двухстадийному
кинетическому механизму:
EDA2,DB2A
21
kk
.

118
Известны входные концентрации исходных веществ и константы скорости
отдельных стадий реакции, соответствующие заданной температуре процесса:
k
1
=0.3, k
2
=0.9 при t
0
A
0
=2, B
0
=1.6.
Математическая модель реактора для любого времени пребывания – t в этих
условиях представлена системой уравнений:
DAk
dt
dE
DAkABk
dt
dD
ABk2
dt
dB
DAk2ABk
dt
dA
2
2
2
2
2
1
2
1
2
2
2
1
Решение этой системы с соответствующими начальными и граничными
условиями выполнено методом Рунге-Кутта. На рисунке 6.4 представлены
числовые и графические результаты решения.
k1
0.3
k2
0.9
tn
0
tk 10
c0
2
1.6
0
0
fr1 v1 v2( ) k1 v1 v2
2
fr2 v3( ) k2 v3
2
D t c( )
fr1 c
1
c
2
2 fr1 c
1
c
2
fr1 c
1
c
2
2 fr2 c
3
fr2 c
3
Z rkfixed c0 tn tk 100 D( )
j 1 100
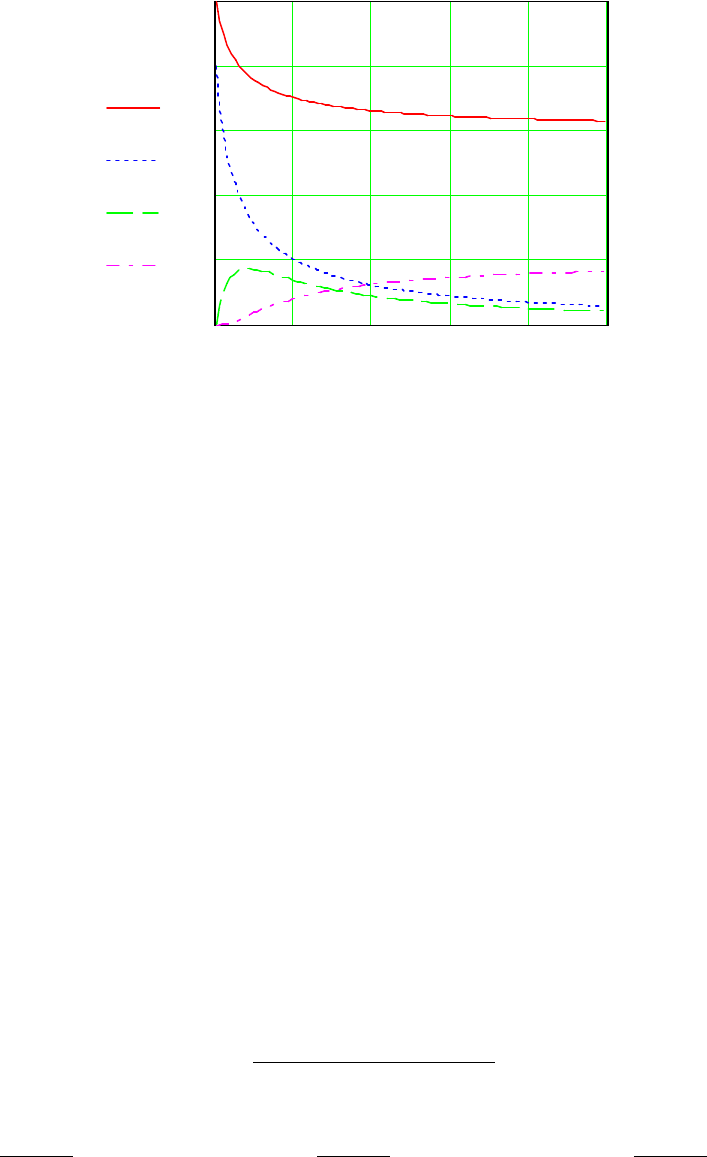
119
0 2 4 6 8 10
0
0.4
0.8
1.2
1.6
2
Z
j 2
Z
j 3
Z
j 4
Z
j 5
Z
j 1
Рисунок 6.4 – Результаты моделирования трубчатого реактора
6.2.4 Моделирование процесса окисления ксилола до фталевого ангидрида
в трубчатом реакторе
В трубчатом реакторе протекает процесс окисления ксилола (A) до фталевого
ангидрида (B), который упрощённо можно представить в следующем виде:
COA
COB
BOA
3
2
1
k
2
k
2
k
2
Последняя из реакций учитывает образование в процессе химического
превращения продуктов реакции (C): CO и CO
2.
Скорости реакций по компонентам
имеют следующий вид:
22
22
2
OB2OA3C
OB2OA1B
OA31A
mmKmmKr
mmKmmKr
mm)KK(r
где
m
- мольные доли соответствующих веществ.
Константы скоростей реакций
часторакгкатализа
кмоль
зависят от температуры:
768.27
T
R
28600
3Kln 878.25
T
R
31400
2Kln 745.26
T
R
27000
1Kln
Математическое описание реактора состоит из уравнений материального и
теплового балансов:

120
dcG
)TT(U4
r
cG
)3H(ρ
r
cG
)1H(ρ
dl
dT
xxx
r
Gm
Mρ
dl
dx
r
Gm
Mρ
dl
dx
P
х
C
P
B
P
CBA
C
A
C
B
A
B
0
0
Граничные условия: на входе в реактор при l=0:
0
AACB
mm,0x,0x,TввT
Здесь приняты следующие обозначения:
0
0
A
AA
A
m
mm
x
,
AA
B
B
mm
m
x
0
,
AA
C
C
mm
m
x
0
Таблица 6.1 – Спецификация принятых обозначений и размерность параметров
Обозначения Наименование Размерность
ρ
Плотность катализатора
3
м
кг
(-H1), (-H2), (-H3)
Тепловые эффекты
реакций
кмоль
ккал
G
Поверхностная массовая
скорость
часм
кг
2
с
P
Удельная массовая
теплоемкость
Ккг
ккал
l
Текущая длина реактора
м
d
Диаметр реактора
м
U
Коэффициент
теплопередачи
Кчасм
ккал
2
T, T
х
Температуры в реакторе
и охлаждающего агента
К
M
Мольная масса
кмоль
кг
2
OCBA
m,m,m,m
Мольные доли
соответствующих
веществ, индекс 0
относит
соответствующую
величину к входу в
реактор
Ниже производится расчёт параметров процесса в пакете Mathcad.
ro 1300
M 0.02948
G
4684
cp
0.25
U
82.7
ma0 9.27 10
3
Hl
307
H3 1090
mO2
0.208
Tbx 650
d 0.025
b1 ro
M
G ma0
q ro
Hl
G cp
z ro
H3
G cp
