Холоднов В.А. Системный анализ и принятие решений. Компьютерное моделирование и оптимизация объектов химической технологии в MathCad и Excel
Подождите немного. Документ загружается.


131
vii- L – длина реактора,
viii- k – константа скорости реакции,
ix- xf – точка, в которой ищется решение,
x- C
вx
– концентрация исходного компонента.
– граничные условия,
– условия стыковки решений в точке x = xf.
После этого выполняется обращение к функции для решения краевой задачи.
Диффузионная модель реактора второго порядка представлена следующей
системой из двух уравнений первого порядка:
12
2
2
1
y
Dl
k
y
Dl
v
dl
dy
y
dl
dy
Функция bvalfit(v1, v2, x1, x2, v, D, load1, load2, score) возвращает недостающие
значения s1=0.854 и s2=0.032 для расчета начальных значений y1 и y2, после
чего вычисляется концентрация компонента на выходе из реактора С=0.032
3
м
кмоль
.Это значение совпадает с точным значением.
Ниже представлен пример моделирования однопараметрической диффузионной
модели стационарного химического реактора при протекании в нём реакции
первого порядка в системе Mathcad.
v
0.1
L 10
k
0.04
xf
2
Cbx
1
Dl
0.05
Pe v
L
Dl
Pe 20
v1
1
0.6
Задание недостающих стартовых значений для y1
и y2
v2
1
0.2
Задание граничных условий
при l=0
load1 x1 v1( )
v1
1
v
Dl
v1
1
v
Dl
Cbx
при I=L
load2 x2 v2( )
v2
1
0
Условие, приводящее к стыковке решений в точке х=хf
score xf y( )
y
S bvalfit v1 v2 0 10 xf D load1 load2 score( )
S 0.854 0.032( )
S S
T
132
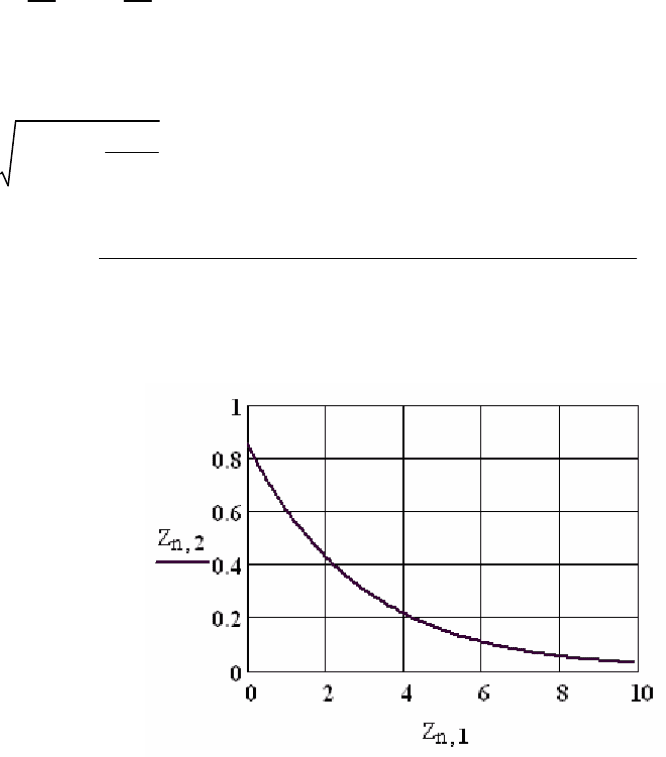
Рисунок 6.10 – Исследование однопараметрической диффузионной модели
стационарного химического реактора при протекании в нём реакции первого
порядка в системе Mathcad
6.4 Математическое моделирование на основе решения дифференциальных
уравнений в частных производных
Одним из самых распространенных методов решения уравнений в частных
производных является метод сеток или метод конечных разностей. Решение
может быть найдено в некоторой ограниченной области на плоскости. Область
разбивается параллельными прямыми на участки (ячейки). В узлах сетки
производные заменяются разностными отношениями.
Рассмотрим моделирование динамики трубчатого реактора для химической
реакции, протекающей в две стадии: A+B
D, D+B
E, с известными начальными
и граничными условиями.
Решение такой задачи основано на решении системы дифференциальных
уравнений в частных производных. Для решения разобьём длину реактора на n
равных частей (например, на 6).
Запишем уравнения материального баланса для каждого сечения 1-5 с учётом
двухстороннего определения производной каждого вещества по длине реактора.
y
S
1
v
Dl
S
1
k
Dl
Cbx
Z rkfixed y 0 10 100 D( )
n 1 100
a 1 4 k
L
v Pe
c Cbx 4 a
exp 0.5 Pe( )
1 a( )
2
exp 0.5 a Pe( ) 1 a( )
2
exp 0.5 a Pe( )
c 0.032
133
ii1
1i1ii
bak
l2
aa
v
t
a
ii2ii1
1i1i1
dbkbak
l2
bb
v
t
b
ii2
1i1i1
dbk
l
2
ee
v
t
e
ii2ii1
1i1i1
dbkbak
l
2
dd
v
t
d
Здесь i=1(1)5.
При этом: a
0
=abx, b
0
=bbx, d
0
=dbx, e
0
=ebx.
Для последнего сечения воспользуемся односторонним определением
производной.
nn1
1nnn
bak
l
aa
v
t
a
nn2nn1
1nnn
dbkbak
l
bb
v
t
b
nn2
1nnn
dbk
l
ee
v
t
e
nn2nn1
1nnn
dbkbak
l
dd
v
t
d
Для каждого сечения значения концентраций веществ представим в виде
таблицы 6.4.
Таблица 6.4 – Обозначения концентраций веществ
Вход
реактора
Номер сечения
Выход
реактора
0 1 2 3 4 5 6
abx y1 y5 y9 y13 y17 y21
bbx y2 y6 y10 y14 y18 y22
ebx y3 y7 y11 y15 y19 y23
dbx y4 y8 y12 y16 y20 y24
Ниже представлено решение задачи в Mathcad, а на рисунке 6.11 результаты
решения.
Граничные условия
abx 10
bbx 20
dbx
0
ebx
0
Нулевые начальные условия
i 1
24
y
i
0
Константы скорости
k1
0.1
k2
0.3
Длина реактора
l
5
Линейная скорость
v
1
z
v
2
l
Шаг по длине реактора
l
5
6
134
Сечение 1
Сечение 2
Сечение 3
D t y( )
z abx y
5
k1 y
1
y
2
z bbx y
6
k1 y
1
y
2
k2 y
2
y
3
z dbx y
7
k1 y
1
y
2
k2 y
2
y
3
z ebx y
8
k2 y
2
y
3
z y
1
y
9
k1 y
5
y
6
z y
2
y
10
k1 y
5
y
6
k2 y
6
y
7
z y
3
y
11
k1 y
5
y
6
k2 y
6
y
7
z y
4
y
12
k2 y
6
y
7
z y
5
y
13
k1 y
9
y
10
z y
6
y
14
k1 y
9
y
10
k2 y
10
y
11
z y
7
y
15
k1 y
9
y
10
k2 y
10
y
11
z y
8
y
16
k2 y
10
y
11
z y
9
y
17
k1 y
13
y
14
z y
10
y
18
k1 y
13
y
14
k2 y
14
y
15
z y
11
y
19
k1 y
13
y
14
k2 y
14
y
15
z y
12
y
20
k2 y
14
y
15
z y
13
y
21
k1 y
17
y
18
z y
14
y
22
k1 y
17
y
18
k2 y
18
y
19
z y
15
y
23
k1 y
17
y
18
k2 y
18
y
19
z y
16
y
24
k2 y
18
y
19
z 2 y
17
y
21
k1 y
21
y
22
z 2 y
18
y
22
k1 y
21
y
22
k2 y
22
y
23
z 2 y
19
y
23
k1 y
21
y
22
k2 y
22
y
23
z 2 y
20
y
24
k2 y
22
y
23
Сечение 4
Сечение 5
Сечение 6
Результаты моделирования динамического режима в трубчатом реакторе
Z rkfixed y 0 5 200 D( )
n 1 200
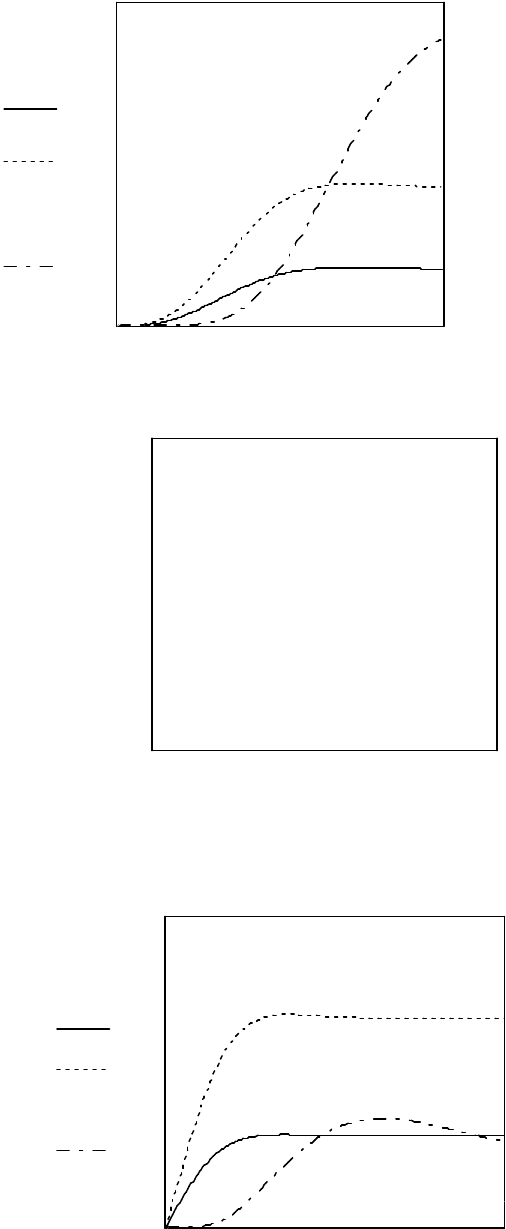
135
0.6
Z
n 14
Z
n 15
Z
n 16
Z
n 17
5Z
n 1
Рисунок 6.11 – Изменение концентраций веществ на выходе из реактора во
времени для химической реакции, протекающей в две стадии: A+B
D, D+B
E
Изменение концентраций веществ А, В, Е, D в соответствующем сечении
во времени
0 1 2 3 4 5
0
2
4
6
8
10
Z
n 10
Z
n 11
Z
n 12
Z
n 13
Z
n 1
t Z
1
d Z
5
e Z
4
b Z
3
a Z
2
0 1 2 3 4 5
0
3
6
9
12
15
a
b
e
d
t
136
6.5 Математическое моделирование динамики теплообменного аппарата
(противоток)
Как известно, математическое описание теплообменного аппарата можно
представить в следующем виде:
)TT(
cm
FK
l
T
v
dt
dT
)TT(
cm
FK
l
T
v
dt
dT
хг
хх
х
х
х
хг
гг
г
г
г
Использованные здесь обозначения представлены в таблице 6.5.
Таблица 6.5 – Спецификация принятых обозначений и размерность параметров
Обозначения Наименование Размерность
K
Коэффициент
теплопередачи
C
час
м
ккал
02
F
Площадь поверхности
теплообмена
2
м
m
Массовый расход
соответствующего потока
час
кг
c
Удельная теплоёмкость
C
кг
ккал
0
t
Время
час
T
Температура
C
0
v
Линейная скорость
соответствующего потока
час
м
Индексы “г” и “х” относят величины к горячему и холодному потоку.
Начальные условия:
при t=0 )l(TT
гг
,
)l(TT
хх
Граничные условия:
при l=0
t
, ?TT
вх,гг
вх,хх
TT
при l=L
t
,
вых,гг
TT
Обозначения в математическом описании представлены в таблице 6.6.
Таблица 6.6 – Обозначения в математическом описании
Вход ТОА Номер сечения Выход ТОА
1 2 3 4 5
?T
вх,г
1,г
T
2,г
T
3,г
T
4,г
T
5,г
T
6,г
T
вх,х
T
1,х
T
2,х
T
3,х
T
4,х
T
5,х
T
6,х
T
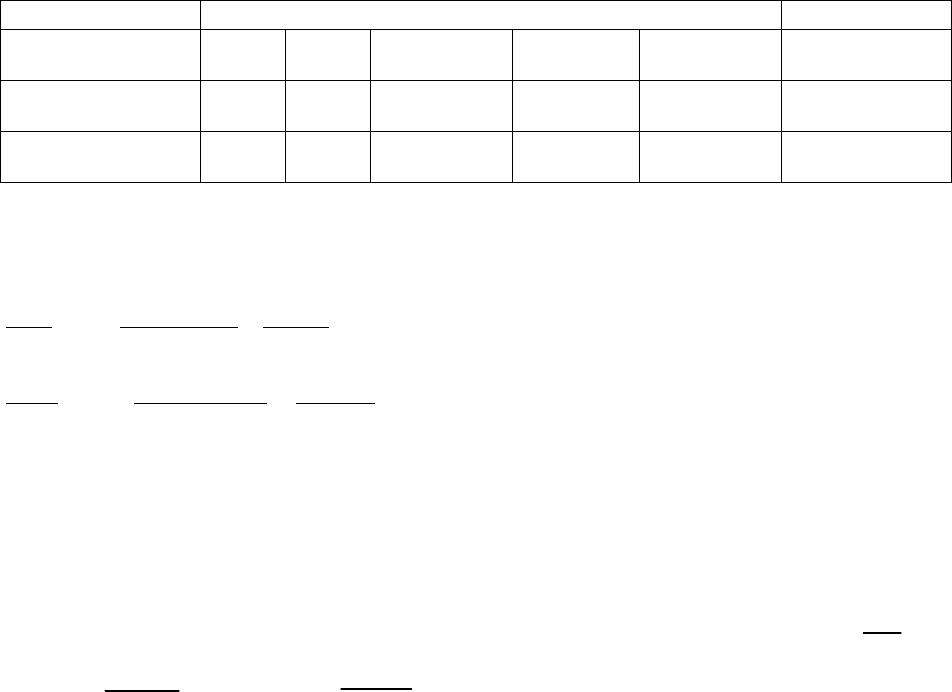
Обозначения в Mathcad представлены в таблице 6.7.
137
Таблица 6.7 – Обозначения в Mathcad
Вход ТОА Номер сечения Выход ТОА
1 2 3 4 5
?T
вх,г
y1 у3 y5 y7 y9 y11
вх,х
T
y2 y4 y6 y8 y10 y12
Запишем уравнения материального баланса для каждого сечения 1-5
с учётом двухстороннего определения производной каждой температуры по
длине реактора.
)TT(
cm
FK
l2
TT
v
t
T
i,xi,г
гг
1i
,г
1i
,г
г
i,г
)TT(
cm
FK
l2
TT
v
t
T
i,хi,г
хх
1i
,х
1i
,х
х
i,х
i=1(1)5
Ниже представлены результаты моделирования ТОА для технологической схемы
получения полиэтилена высокого давления в Mathcad.
Динамика противоточного теплообменника
K 400.0
F
17.86
txbx 20
tgbx
31.23
cx
1
cg
0.6
vg
0.7
vx
0.7
mx
9439
L
1.4
mg 9236
h
L 2
5
a2 K
F
mx cx
a1 K
F
mg cg
a1 1.289
a2 0.757
a
tgbx
b
txbx
y0
a
b
a
b
a
b
a
b
a
b
a
b
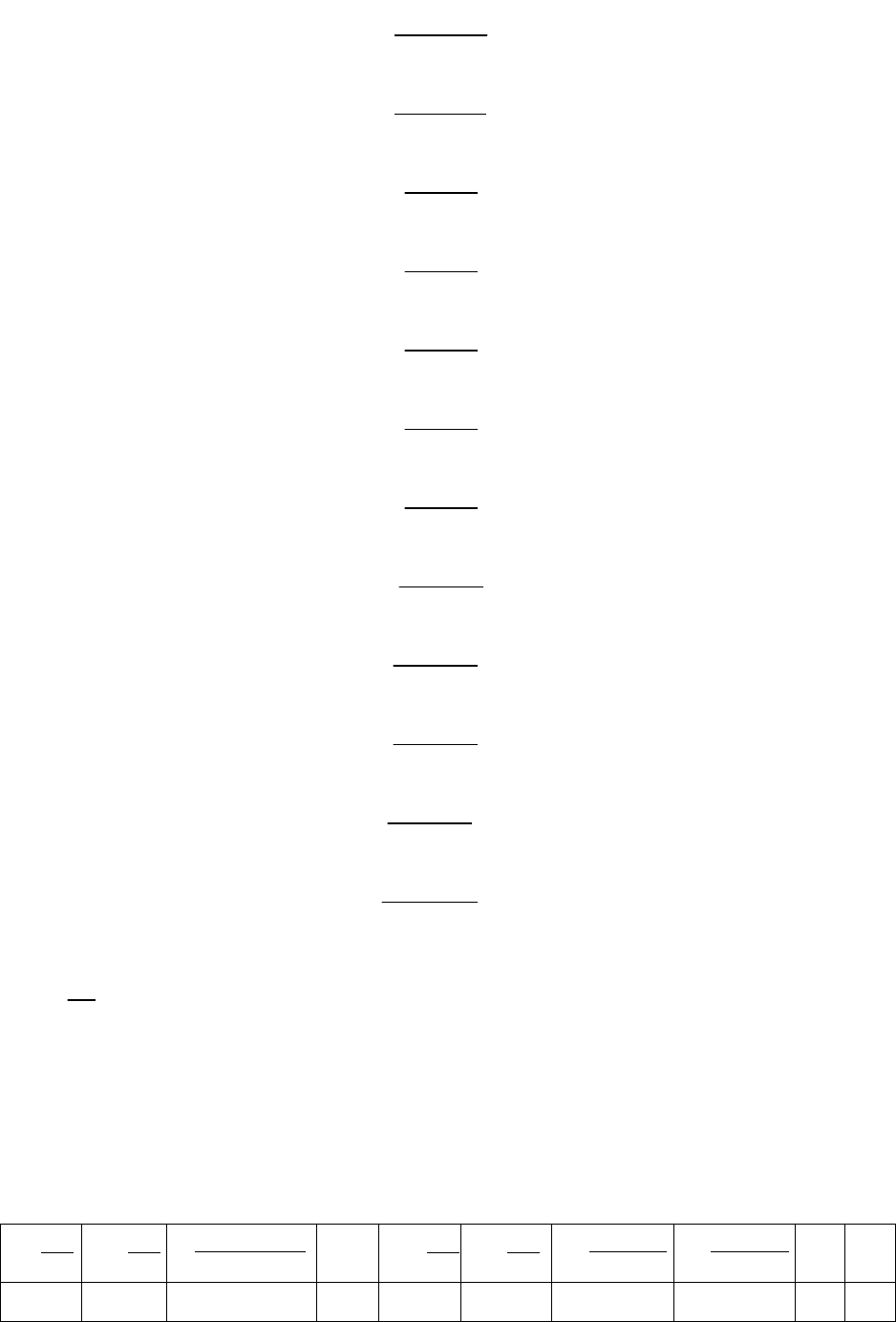
138
D t y( )
vg
y
3
tgbx
h
a1 y
1
y
2
vx
y
4
txbx
h
a2 y
1
y
2
vg
y
5
y
1
h
a1 y
3
y
4
vx
y
6
y
2
h
a2 y
3
y
4
vg
y
7
y
3
h
a1 y
5
y
6
vx
y
8
y
4
h
a2 y
5
y
6
vg
y
9
y
5
h
a1 y
7
y
8
vx
y
10
y
6
h
a2 y
7
y
8
vg
y
11
y
7
h
a1 y
9
y
10
vx
y
12
y
8
h
a2 y
9
y
10
vg
y
11
y
9
0.5 h
a1 y
11
y
12
vx
y
12
y
10
0.5 h
a2 y
11
y
12
Параметры ТОА приведены в таблице 6.8.
Таблица 6.8 – Параметры ТОА
х
v ,
час
м
г
v ,
час
м
K,
градчасм
ккал
2
F,
2
м
х
m ,
час
кг
г
m ,
час
кг
х
c ,
градкг
ккал
г
c ,
градкг
ккал
вх,г
T
вх,х
T
4 4 400 14.6
9439
9236 1 0.67 80 20
tk
L
vg
n 200
nk
n
Z rkfixed y0 0 tk n D( )
n 1 200

139
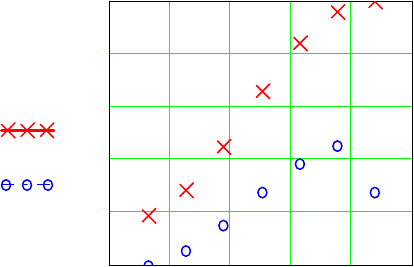
На рисунке 6.12 представлены изменения температур потоков в ТОА в
соответствующем сечении во времени.
Рисунок 6.12 – Изменения температур потоков в ТОА в соответствующем сечении
во времени
Результаты моделирования
tg
1
tgbx
tg
2
Z
2
nk
tg
3
Z
4
nk
tg
4
Z
6
nk
tg
6
Z
10
nk
tg
7
Z
12
nk
tx
4
Z
7
nk
tg
5
Z
8
nk
140
На рисунке 6.13 представлены результаты изменения температур потоков по
длине ТОА.
Рисунок 6.13 – Изменения температур потоков в ТОА по длине
6.6 Моделирование процесса абсорбции аммиака водой из газообразной
смеси
Аммиак извлекается в противоточной насадочной колонне из газообразной
смеси, поступающей сверху в колонну и содержащей аммиак, поглощаемый
водой, которая поступает противотоком снизу колонны. Абсорбция аммиака водой
сопровождается выделением теплоты, которое вызывает повышение
температуры жидкости и, следовательно, приводит к изменениям в равновесных
соотношениях. Математическая модель состоит из следующих уравнений
материального баланса:
tx
1
txbx
tx
2
Z
3
nk
tx
3
Z
5
nk
tx
5
Z
9
nk
tx
6
Z
11
nk
tx
7
Z
7
nk
tg
31.23
36.868
46.695
59.414
70.217
77.283
79.996
tx
20
23.31
29.079
36.547
42.889
47.037
36.547
0 1.6 3.2 4.8 6.4 8
20
32
44
56
68
80
tg
i
tx
i
i
