Inversin R. Allen Micro-hydropower Sourcebook

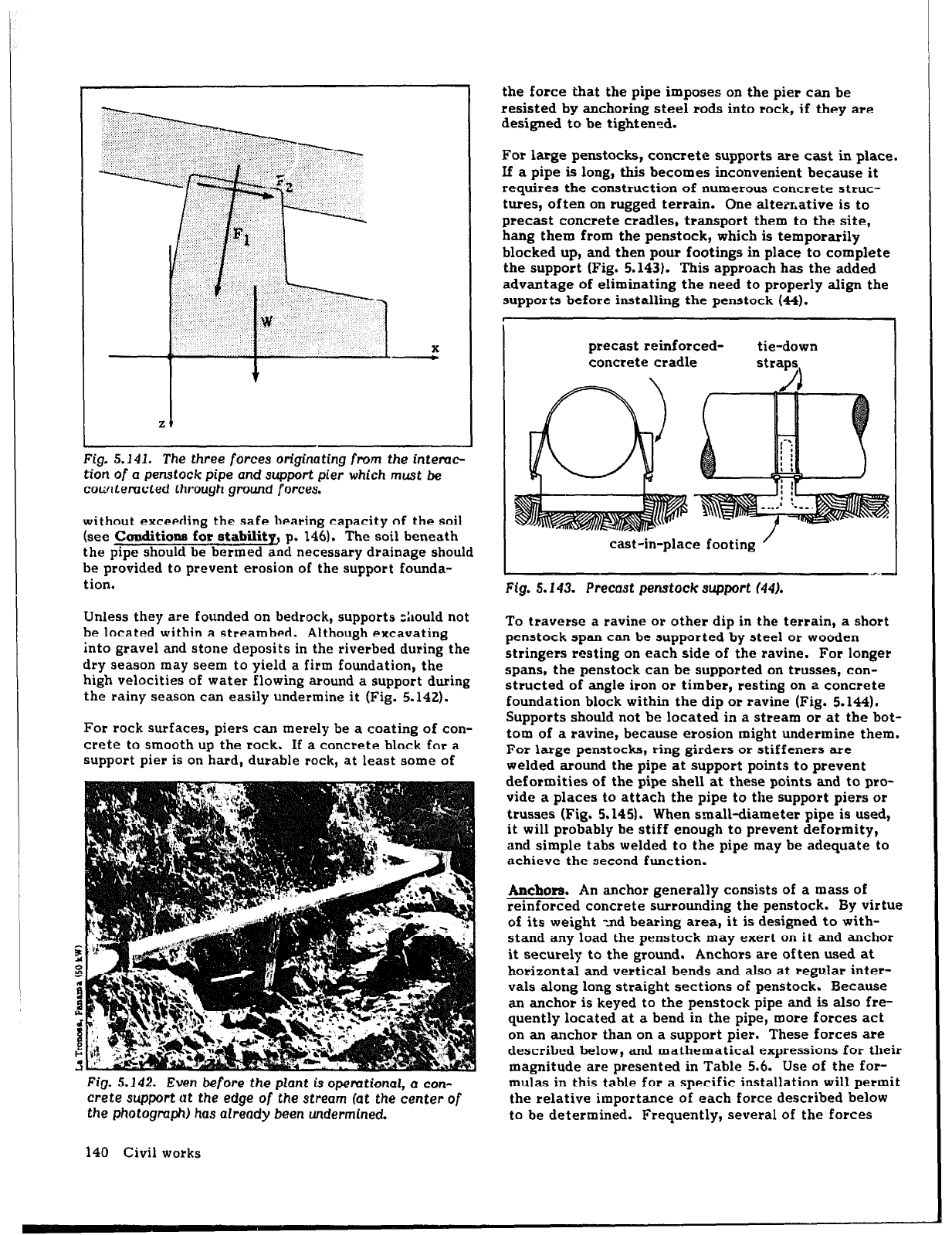
Fig. 5.141. The three

forces

originating

from

the

intemc

tion of a

penstock

pipe and support pier which

must be

cowtemcted

through

ground

forces.

without exceeding the safe bearing capacity of the soil

(see Conditione for stability, p. 146). The soil beneath

the pipe should be bermed and necessary drainage should

be provided to prevent erosion of the support founda-

tion.

Unless they are founded on bedrock, supports c:lould not

be located within a streambed. Although excavating

into gravel and stone deposits in the riverbed during the

dry season may seem to yield a firm foundation, the

high velocities of water flowing around a support during

the rainy season can easily undermine it (Fig. 5.142).

For rock surfaces, piers can merely be a coating of con-

crete to smooth up the rock. If a concrete block for a

support pier is on hard, durable rock, at least some of

Fig, 5.142. Even before

the

plant is

operational, a con-

crete support at the edge of the stream

fat the

center of

the photograph) has already been undermined.

the force that the pipe imposes on the pier can be

resisted by anchoring steel rods into rock, if they are

designed to be tightened.

For large penstocks, concrete supports are cast in place.

If a pipe is long, this becomes inconvenient because it

requires the construction of numerous concrete struc-

tures, often on rugged terrain. One alternative is to

precast concrete cradles, transport them to the site,

hang them from the penstock, which is temporarily

blocked up, and then pour footings in place to complete

the support (Fig. 5.143). This approach has the added

advantage of eliminating the need to properly align the

supports before installing the penstock (44).

precast reinforced-

concrete cradle

tie-down

straps,

cast-in-place footing

/

Fig. 5.143. Precast penstock support (44).

To traverse a ravine or other dip in the terrain, a short

penstock span can be supported by steel or wooden

stringers resting on each side of the ravine. For longer

spans, the penstock can be supported on trusses, con-

structed of angle iron or timber, resting on a concrete

foundation block within the dip or ravine (Fig. 5.144).

Supports should not be located in a stream or at the bot-

tom of a ravine, because erosion might undermine them.

For large penstocks, ring girders or stiffeners are

welded around the pipe at support points to prevent

deformities of the pipe shell at these points and to pro-

vide a places to attach the pipe to the support piers or

trusses (Fig. 5.145). When small-diameter pipe is used,

it will probably be stiff enough to prevent deformity,

and simple tabs welded to the pipe may be adequate to

achieve the second function.

Anchors. An anchor generally consists of a mass of

reinforced concrete surrounding the penstock. By virtue

of its weight -nd bearing area, it is designed to with-

stand any load the penstock may exert on it and anchor

it securely to the ground. Anchors are often used at

horizontal and vertical bends and also at regular inter-

vals along long straight sections of penstock. Because

an anchor is keyed to the penstock pipe and is also fre-

quently located at a bend in the pipe, more forces act

on an anchor than on a support pier. These forces are

described below, and mathematical expressions for their

magnitude are presented in Table

5.6.

Use of the fot-

mulas in this table

for

a specific installation will permit

the relative importance of each force described below

to be determined. Frequently, several of the forces

140 Civil works

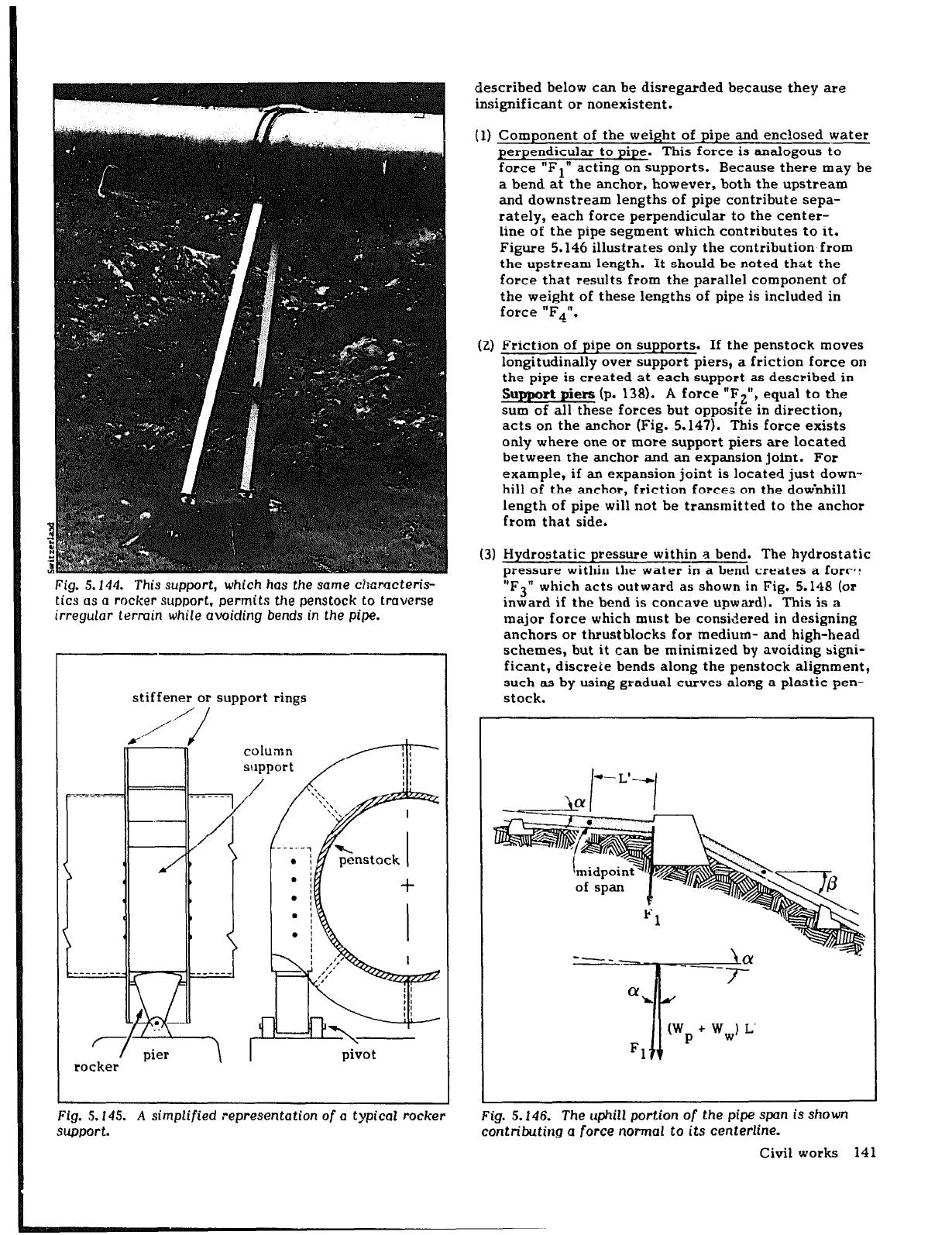
Fig. 5. f44. This support, which

has the same clxmcteris-

tics as a rocker support, permits the penstock to traverse

irregular terrain while avoiding bends in the pipe.

stiffener or support rings

,A---

/’

/

r--II

column

support

rocker

pivot

described below can be disregarded because they are

insignificant or nonexistent.

(1) Component of the weight of pipe and enc!osed water

.-

perpendicular to pipe. This force is analogous to

force “Fl”

acting on supports. Because there may be

a bend at the anchor, however, both the upstream

and downstream lengths of pipe contribute sepa-

rately, each force perpendicular to the center-

line of the pipe segment which contributes to it.

Figure 5.146 illustrates only the contribution from

the upstream length. It should be noted that the

force that results from the parallel component of

the weight of these lengths

of

pipe is included in

force “F4”.

(2) Friction of pipe on supports. If the penstock moves

longitudinally over support piers, a friction force on

the pipe is created at each support as described in

Support piers (p. 138). A force “F2”, equal to the

sum of all these forces but opposite in direction,

acts on the anchor (Fig. 5.147). This force exists

only where one

or

more support piers are located

between the anchor and an expansion joint. For

example, if an expansion joint is located just down-

hill of the anchor, friction forces on the dow’nhill

length of pipe will not be transmitted to the anchor

from that side.

(3) Hydrostatic pressure within a bend. The hydrostatic

pressure within the water in a bend creates a forr,t

“F3” which acts outward as shown in Fig. 5.148 (or

inward if the bend is concave upward). This is a

major force which must be considered in designing

anchors or thrustblocks for medium- and high-head

schemes, but it can be minimized by avoiding signi-

ficant, discreie bends along the penstock alignment,

such as by using gradual curves along a plastic pen-

stock.

Fig. 5. I45. A simplified representation of a typical

rocker

support.

Fig.

5.146. The uphill portion

of

the

pipe span is

shown

contributing a force normal to

its

centerline.

Civil works 141

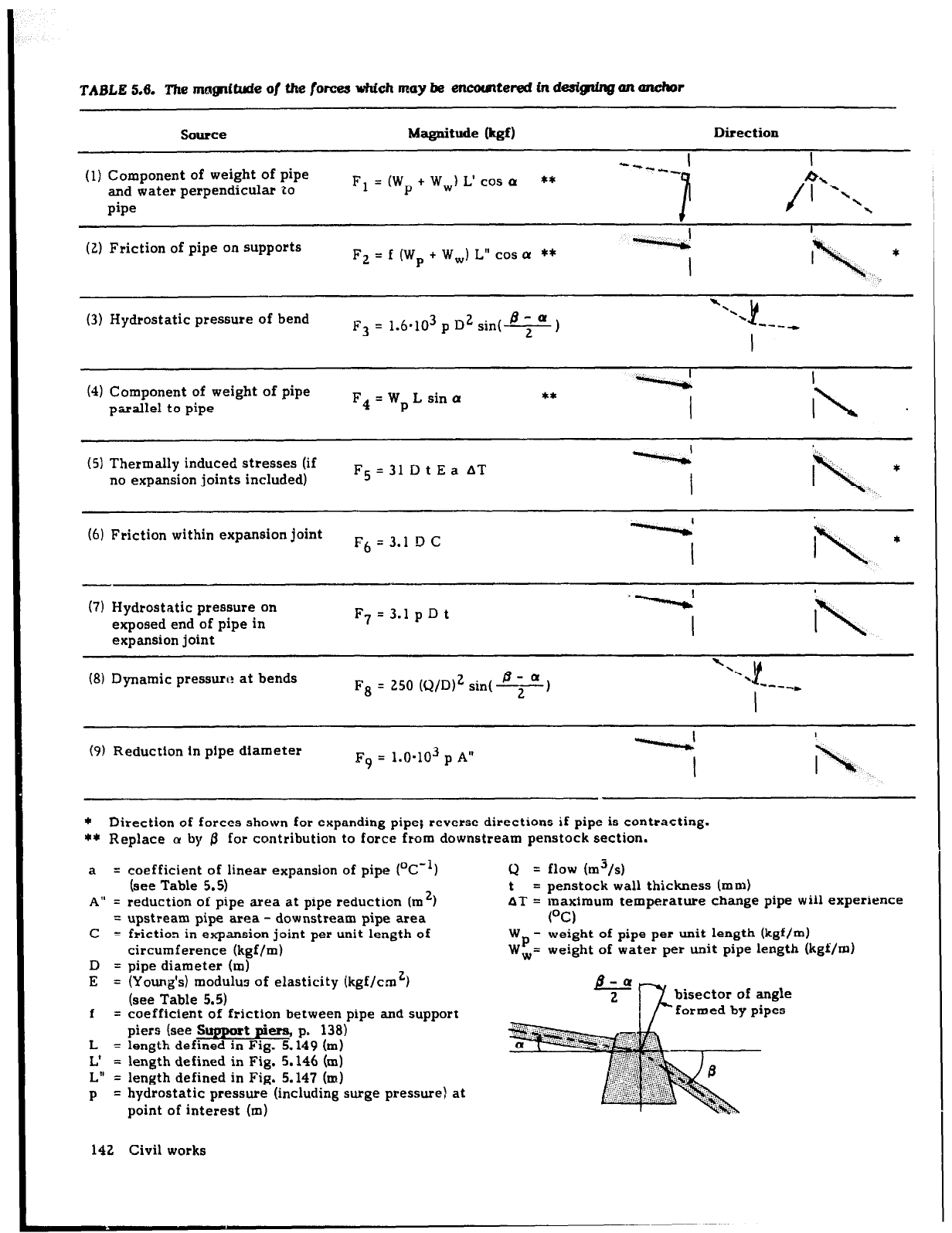
TABLE 5.6.

The mag~ffufe of Uw force3 vhf& may he encomtered fn desff@q an anchor

Source Magnitde kf)

Direction

(1) Component of weight of pipe

and water perpendicular

20

pipe

F1 = (Wp + Ww) L’ cos P **

(2) Friction of pipe on supports

F2 = f (W

P

+ Ww) L” cos a **

(3) Hydrostatic pressure of bend B-a

F3 = 1.6.103 p D2 sin(T)

‘-.

---+

I

(4) Component of weight of pipe

4

I

F4 = Wp L sin a

**

parallel to pipe

I

(5) Thermally induced stresses (if

----4!

:.:

no expansion joints included)

F5 = 31 D t E a AT

I

I\...

*

(6) Friction within expansion joint

F6 = 3.1 D c

----a!

I

(7) Hydrostatic pressure on

exposed end

of

pipe in

expansion joint

(8) Dynamic pressurt? at bends

F7=3.1pDt

B-a

F8 = 250 (Q/D)’ sin( 2)

(9) Reduction in pipe diameter

Fq = 1.0.103 p A”

* Direction of forces shown for expanding pipe; reverse directions if pipe is contracting.

** Replace a by fi for contribution to force from downstream penstock section.

a = coefficient of linear expansion of pipe (OC-‘)

(see Table 5.5)

A” = reduction of pipe area at pipe reduction (m2)

= upstream pipe area - downstream pipe area

C = friction in expansion joint per unit length of

circumference (kgf/m)

D = pipe diameter (m)

E

= (Young’s) modulus of elasticity (kgf/cm’)

(see Table 5.5)

f

= coefficient of friction between pipe and support

piers (see Support piers, p. 138)

L = length defined in Fig. 5.149 (m)

L’ = length defined in Fig. 5.146 (m)

L”

= length defined in Fig. 5.147 (m)

P

= hydrostatic pressure (including surge pressure) at

point of interest (m)

142 Civil works

Q = flow (m”/s)

t

= penstock wall thickness (mm)

AT = maximum temperature change pipe will experience

(OC)

Wp = weight of pipe per unit length (kgf/m)

W,= weight of water per unit pipe length (kgf/m)

bisector of angle

formed by pipes

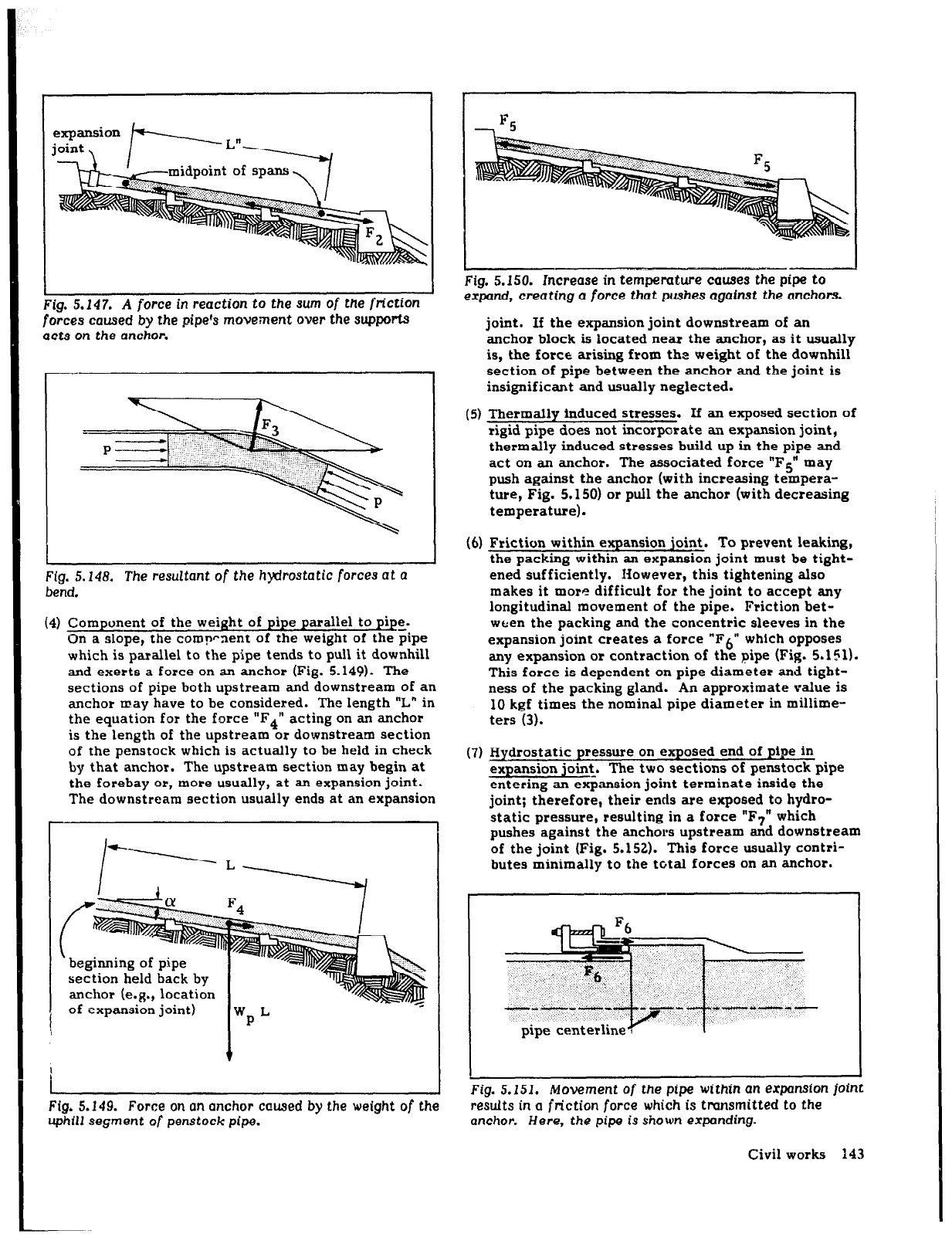
Fig. 5.147. A

force in

reaction to the

sum

of the friction

forces caused

by the

Pipe% movement over the supportS

acts

on the

anchor.

Fig. 5.148. The resultant of the hydrostatic forces at

a

bend.

(4) Component of the weight of pipe parallel to pipe.

On a slope, the comprnent of the weight of the pipe

which is parallel to the pipe tends to pull it downhill

and exerts a force on an anchor (Fig. 5.149). The

sections of pipe both upstream and downstream of an

anchor may have to be considered. The length “L” in

the equation for the force “F4” acting on an anchor

is the length of the upstream or downstream section

of the penstock which is actually to be held in check

by that anchor. The upstream section may begin at

the forebay or, more usually, at an expansion joint.

The downstream section usually ends at an expansion

’ beginning of pipe

section held back by

anchor (e.g., location

.s

1

of expansion joint)

wP L

+

I

Fig. 5.149. Force on an anchor caused by the weight of the

uphill

segment

of penstock

pipe.

Fig. 5.150. Increase in temperature causes

the

pipe to

expand, creating

a force that pushes against the anchors.

joint. If the expansion joint downstream of an

anchor block is located near the anchor, as it usually

is, the force arising from the weight of the downhill

section of pipe between the anchor and the joint is

insignificant and usually neglected.

(5) Thermally induced stresses. If an exposed section of

rigid pipe does not incorporate an expansion joint,

thermally induced stresses build up in the pipe and

act on an anchor. The associated force “F5” may

push against the anchor (with increasing tempera-

ture, Fig. 5.150) or pull the anchor (with decreasing

temperature).

(6) Friction within expansion joint. To prevent leaking,

the packing within an expansion joint must be tight-

ened sufficiently. However, this tightening also

makes it more difficult for the joint to accept any

longitudinal movement

of

the pipe. Friction bet-

ween the packing and the concentric sleeves in the

expansion joint creates a force “F6” which opposes

any expansion or contraction

of

the pipe (Fig. 5.151).

This force is dependent on pipe diameter and tight-

ness of the packing gland. An approximate value is

IO kgf times the nominal pipe diameter in millime-

ters (3).

(7) Hydrostatic pressure on exposed end of pipe in

expansion joint, The two sections of penstock pipe

entering an exptansion joint terminate inside the

joint; therefore, their ends are exposed to hydro-

static pressure, resulting in a force “F7” which

pushes against the anchors upstream and downstream

of the joint (Fig. 5.152). This force usually contri-

butes minimally to the total forces on an anchor.

Fig. 5.151. Movement

of

the pipe within an expansion

joint

results in a friction

force

which is transmitted to the

anchor. Ilere, the pipe is shown expanding.

Civil works 143

(8) Dynamic pressure at bend. At the bend, the water

changes the direction of its velocity and therefore

the direction of its momentum (Fig. 5.153). This

requires that the bend exert a force on the water.

Consequently, an equal but opposite reaction force

“Fg” acts on the bend; it acts in the direction which

bisects the exterior angle of the bend. Because

velocities in penstocks are relatively low, the magni-

tude of this force is usually insignificant.

(9) Reduction of pipe diameter. If there is a change in

the diameter of the penstock, the hydrostatic pres-

sure acting on the exposed area creates a force “F9”

which acts in the direction of the smaller-diameter

pipe (Fig. 5.154).

Fig. 5.152. Hydrostatic

pressure

acting

on the exposed end

of

an expansion

joint

remAt.

in a force which is usually

Insignificant.

If a section of a penstock is located near a stream and

might be submerged during a flood, another force must

be considered: the force that arises from buoyancy if

the penstock becomes empty during a flood. This force

could be counteracted by encasing that penstock section

with concrete. This also protects the penstock from

boulders and other riverbome debris. Although gabion

or timber shields also can be used to protect the pipe,

they may not provide the force necessary to counteract

buoyancy.

P, =

-Fw= Qpvi - QpTo

= Qpvi + (-Qp’j,)

F8 =

2QpV

sin ( 2

B-ul)

Ffg. 5.153. Force caused by

dynamic

pressure is the vector

difference between the momentum of the water into and

out of

the pipe.

\ reducer

Fig.

5.154.

Hydrostatic

pressure

acting

on the walls

of

the

pipe reducer results

in a force on the

anchor.

To ensure a proper key with the foundation, the founda-

tion for the anchor block should be a serrated rock or

soil surface (Fig. 5.155). To ensure a proper key bet-

ween a steel penstock and concrete anchor, steel tabs

can be welded or riveted to the pipe at this point

(Fig. 5.156).

Although an anchor is usually designed so that its weight

is used to counteract the numerous forces imposed on it

by the penstock, steel rods anchored into hard rock can

also contribute to this task. If the rods can be tightly

secured

to the rock, they can keep these forces in

check, and the weight and therefore the size of the

anchor can be reduced.

‘Ihru&bIocks. These are a specialized form of anchor

whose sole purpose is to transmit forces primarily

caused by hydrostatic pressures “F3”, which are concen-

trated at distinct bends along a buried penstock, to

undisturbed soil which provides the reaction force. But

if the force “F3

” is vertically upward, an anchor is still

Fig. 5.155. A sermted surface ensures

proper key between

anchor and

fowIdation.

144 Civil works

Fig. 5.156. Flanges are welded to the penstock bend to key

it

to

the

reinforced-concrete anchor located

at

the top

of

the final drop to the powerhouse.

used if the soil above a thrustblock is not able to resist

this force. At gradual bends, these forces are uniformly

distributed along the pipe, and soil which has been prop-

erly backfilled can easily resist the low foundation pres-

sures which result. If there is a sudden reduction of

pipe area, a thrustblock would also be required to

transmit the associated force “F9”.

The magnitude and direction of the principal force act-

ing on a thrustblock are defined by force “F3” in

Table 5.6. Because buried pipe is not subject to large

temperature changes, expansion joints are not used and

forces “F

of low

“, “F5”, “F6”, and “F7” do not arise. Because

ve ocities in a penstock, the force “Fs” caused by F

dynamic pressure at a bend is negligible. The forces

“Fl” and “F4” resulting from the weight of the pipe are

distributed along the entire length of penstock and

resisted by the soil.

A thrustblock is commonly a block of concrete poured

after the pipe is

in

place. It is placed in a position to

transmit the force acting on it to the ground. The

thrustblock should be no higher than half the distance

from the ground surface to its base (Fig 5.157); other-

wise, the soil may not offer sufficient resistance to

properly restrain the thrustblock (10). The face of the

thrustblock must be approximately perpendicular to the

force it is to transmit.

Reducing the forces acting on a structure. In a previous

section, a number of forces which a penstock pipe can

exert on a support pier, anchor, or thrustblock were dis-

cussed. The next step is to design each of these struc-

tures to resist these forces. It is first necessary to sim-

plify the problem by reducing all the forces that act on

the structure to a single force that acts at a specific

excavated

trench

tie-down rods

Section AA

Fig. 5.157. Proper placement

of

a thrustblock at a bend in

a penstock

point. When this has been done, the stability of a given

design can be determined.

In order to explain the procedure to be used as simply as

possible, assume that the only bend at an anchor is in a

vertical plane. If this were not the case, forces would

need to be resolved in two perpendicular vertical planes,

one plane usually including the pipe which enters the

anchor. Each force would have to bc resolved carefully

along three perpendicular directions. In this case, the

reduction of forces and conditions for stability discussed

below would still be valid, but application of these ideas

becomes more involved.

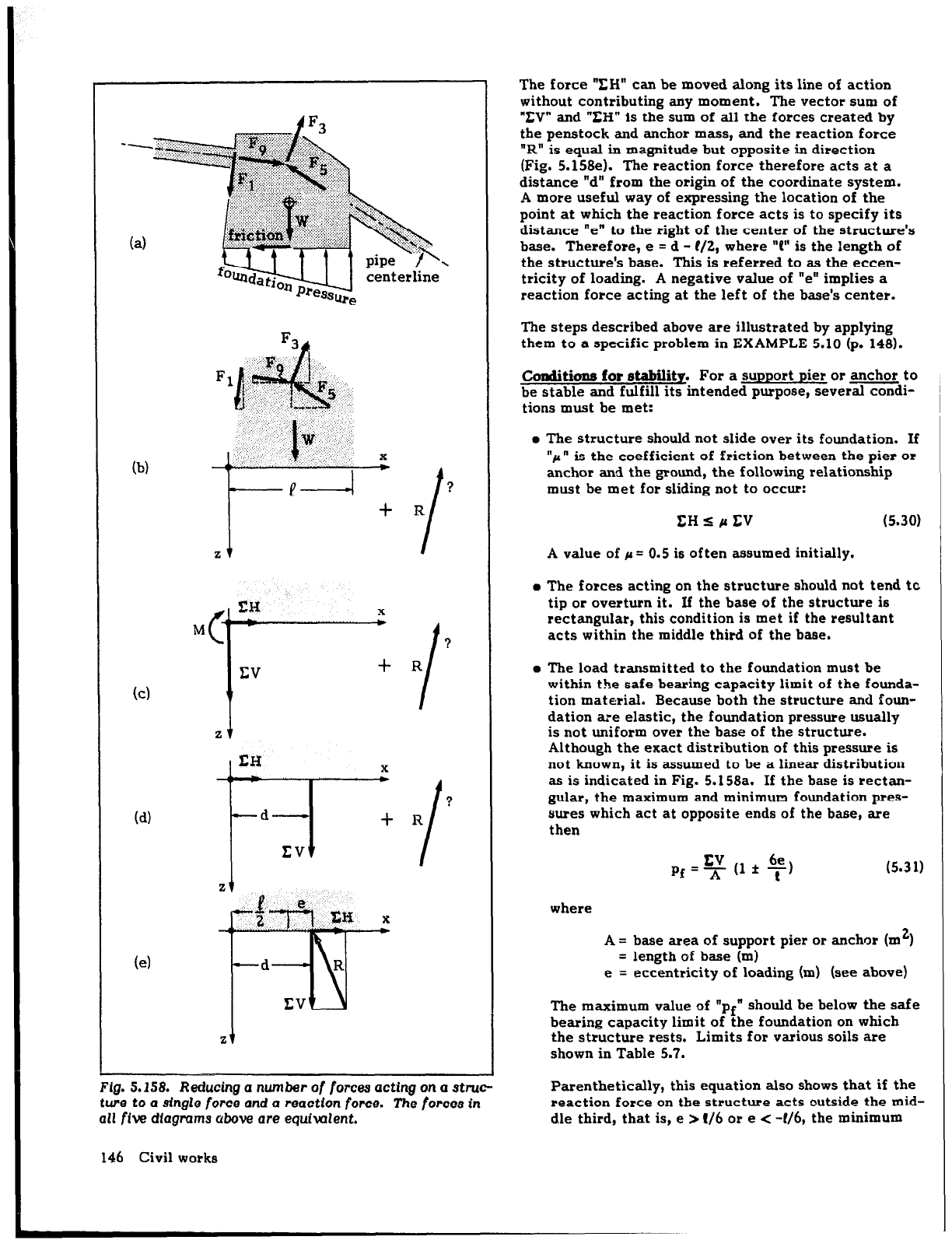
Assume that a structure is being acted upon by the

forces shown in Fig. 5.158(a). In addition to the forces

described previously, the combined weight “W” of the

concrete mass plus pipe and water within the mass

which acts at the center of gravity of the anchor is also

included.

In reaction to all these forces, the foundation exerts an

initially unknown foundation pressure and friction force

over the base of the anchor. The net effect of the fric-

tion and foundation pressure is identical to, and can be

replaced mathematically with, a reaction force “R” act-

ing at an undetermined point on the anchor with a direc-

tion and magnitude yet to be determined (Fig. 5.158bl.

A first step in reducing the penstock forces and weight

of an anchor to a single force is to resolve each force

into components parallel to the x and z axes. The ori-

ginal forces are then equivalent to the sum of all the

horizontal components “EIi” and the sum of all the ver-

tical components ‘ZV” acting along the x and z axes,

respectively, plus a moment “EM” resulting from all the

forces around the origin (Fig. 5.158~).

By translating the net vertical force “EV” a distance “d”

to the right such that

CM

= d IX, the force ‘?X” acting

at a new point (Fig. 5.1586) is equivalent to the same

force acting at the origin plus the moment.

Civil works 145

(4

(d)

(4

Fig. 5.158. Reducing

a

number of forces

acting

on

a struc-

ture to a single force and a reaction force. The forces in

all five dtagmms ubove are equiwlent.

146 Civil works

The force “ZH” can be moved along its line of action

without contributing any moment. The vector sum of

“XV” and “fH” is the sum of all the forces created by

the penstock and anchor mass, and the reaction force

“R” is equal in magnitude but opposite in direction

(Fig. 5.158e). The reaction force therefore acts at a

distance “d” from the origin of the coordinate system.

A more useful way of expressing the location of the

point at which the reaction force acts is to specify its

distance “e” to the right of the center of the structure’s

base. Therefore, e = d - f/2, where “9” is the length of

the structure’s base. This is referred to as the eccen-

tricity of loading. A negative value of “e” implies a

reaction force acting at the left of the base’s center.

The steps described above are illustrated by applying

them to a specific problem in EXAMPLE 5.10 (p. 148).

coldit.ions for etabilit~ For a support pier or anchor to

be stable and fulfill its intended purpose,

several

condi-

tions must be met:

l

The structure should not slide over its foundation. If

“c” is the coefficient of friction between the pier or

anchor and the ground, the following relationship

must be met for sliding not to occur:

CHliicCV

(5.30)

A value of /r = 0.5 is often assumed initially.

l

The forces acting on the structure should not tend tc.

tip

or

overturn it. If the base of the structure is

rectangular, this condition is met if the resultant

acts within the middle third of the base.

a The load transmitted to the foundation must be

within the safe bearing capacity limit of the founda-

tion material. Because both the structure and foun-

dation are elastic, the foundation pressure usually

is not uniform over the base of the structure.

Although the exact distribution of this pressure is

not known, it is assumed to be a linear distribution

as is indicated in Fig. 5.158a. If the base is rectan-

gular, the maximum and minimum foundation pres-

sures which act at opposite ends of the base, are

then

pf =y (1 f

p,

(5.3 1)

where

A= base area of support pier or anchor (m’)

= length of base (m)

e = eccentricity of loading (m) (see above)

The maximum value of “pf” should be below the safe

bearing capacity limit of the foundation on which

the structure rests. Limits for various soils are

shown in Table 5.7.

Parenthetically, this equation also shows that if the

reaction force on the structure acts outside the mid-

dle third, that is, e > f/6 or e < -l/6, the minimum

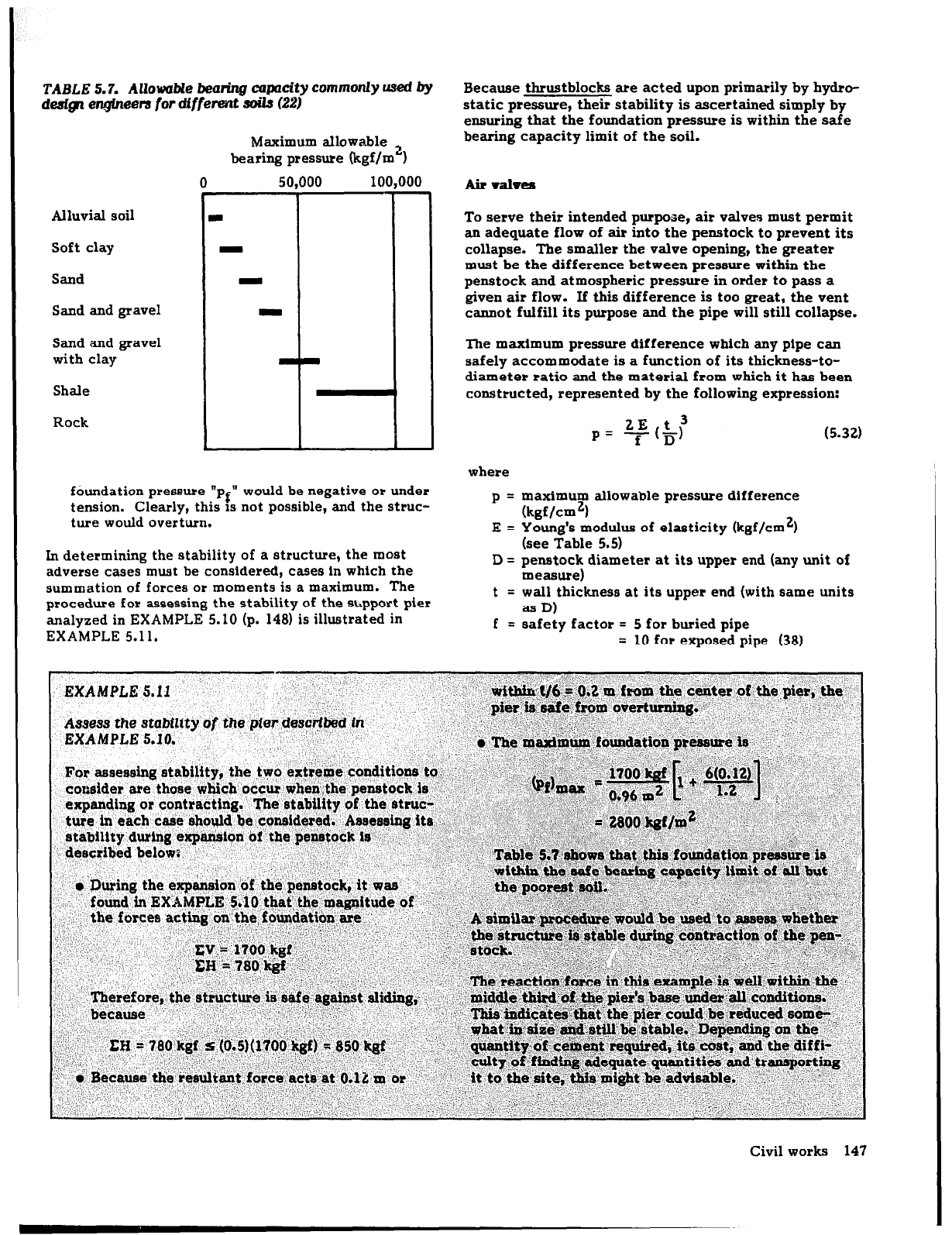
TABLE 5.7.

Allouable bearing capacity commonly used by

design engineen

for dfffemt soils (22)

Maximum allowable

bearing pressure (kgf/m’)

0

50,000

lQ0,000

Alluvial soil

Soft clay

Sand

Sand and gravel

with clay

Shale

Rock

Because thrustblocks are acted upon primarily by hydro-

static pressure, their stability is ascertained simply by

ensuring that the foundation pressure is within the safe

bearing capacity limit of the soil.

To serve their intended purpose, air valves must permit

an adequate flow of air into the penstock to prevent its

collapse. The smaller the valve opening, the greater

must be the difference between pressure within the

penstock and atmospheric pressure in order to pass a

given air flow. If this difference is too great, the vent

cannot fulfill its purpose and the pipe will still collapse.

The maximum pressure difference which any pipe can

safely accommodate is a function of its thickness-to-

diameter ratio and the material

from

which it has been

constructed, represented by the following expression:

P=

zs(L,’

foundation pressure “pf ” would be negative or under

tension. Clearly, this IS not possible, and the struc-

ture would overturn.

In determining the stability of a structure, the most

adverse cases must be considered, cases in which the

summation of forces or moments is a maximum. The

procedure for assessing the stability of the support pier

analyzed in EXAMPLE 5.10 (p. 148) is illustrated in

EXAMPLE 5.11.

where

p = maximum allowable pressure difference

(kgf/cm2)

E = Young’s modulus of elasticity (kgf/cm2)

(see Table 5.5)

D = penstock diameter at its upper end (any unit of

measure)

t = wall thickness at its upper end (with same units

as D)

I = safety factor = 5 for buried pipe

= 10 for exposed pipe (38)

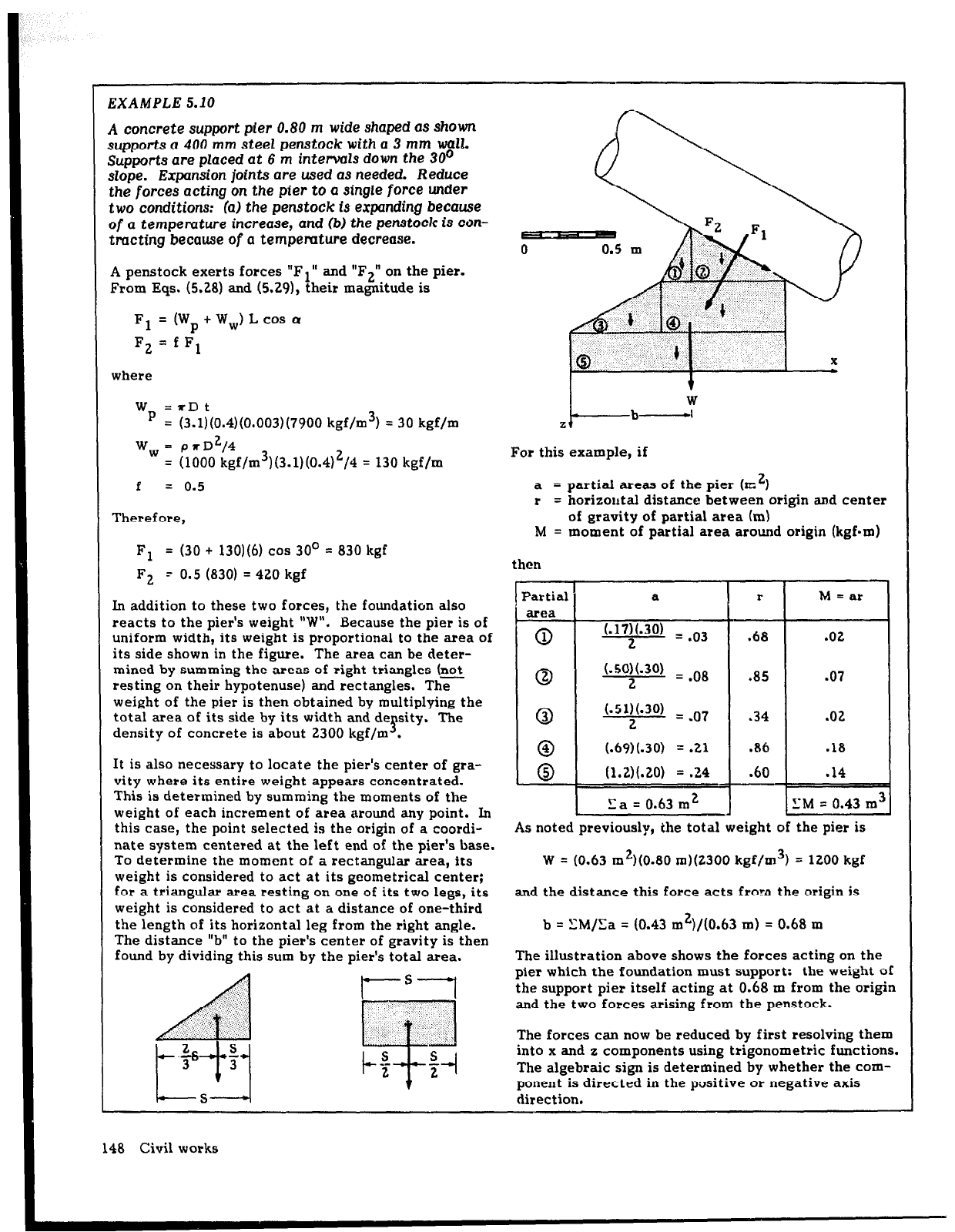
EXAMPLE 5.10

A concrete support pier 0.80 m wide shaped as shown

supports a 400 mm steel penstock with a 3 mm wall.

Supports are placed at 6 m intervals down the 30’

slope. Expansion joints are used as needed. Reduce

the forces acting on

the

pier to a

single force

under

two

conditions: (a) the penstock is expanding because

of a

temperature increase, and (b) the penstock is con-

tracting because

of

a tempemture decrease.

A penstock exerts forces “Fl” and “F2” on the pier.

From Eqs. (5.28) and (5.29), their magnitude is

F1 = (Wp+Ww)Lcoso

F2 = f F1

where

Wp =rDt

= (3.1)(0.4)(0.003)(7900 kgf/m3) = 30 kgf/m

W, = prD2/4

= (1000 kgf/m3)(3.1)(0.4)2/4 = 130 kgf/m

f

= 0.5

Therefore,

Fl

= (30 + 130)(6) cos 30’ = 830 kgf

F2 - 0.5 (830) = 420 kgf

In addition to these two forces, the foundatiun also

reacts to the pier’s weight “W”. Because the pier is of

uniform width, its weight is proportional to the area of

its side shown in the figure. The area can be deter-

mined by summing the areas of right triangles (not

resting on their hypotenuse) and rectangles. The’

weight of the pier is then obtained by multiplying the

total area of its side by its width and de

5

sity. The

density of concrete is about 2300 kgf/m .

It is also necessary to locate the pier’s center of gra-

vity where its entire weight appears concentrated.

This is determined by summing the moments of the

weight of each increment of area around any point. In

this case, the point selected is the origin of a coordi-

nate system centered at the left end of the pier’s base.

To determine the moment of a rectangular area, its

weight is considered to act at its geometrical center;

for a triangular area resting on one of its two legs, its

weight is considered to act at a distance of one-third

the length of its horizontal leg from the right angle.

The distance “b” to the pier’s center of gravity is then

found by dividing this sum by the pier’s total area.

148 Civil works

I-

t

W

b-1

Z

For this example, if

a

= partial areas of the pier (rc’)

r

= horizontal distance between origin and center

of gravity of partial area (m)

M = moment of partial area around origin (kgfmm)

then

Partial

area

0

1

0

@

0

a

(.17)(.3(l) = -03

2

(.50)(.30)

= l 08

2

(.51)(.3(l) = V07

2

(.69)(.30)

= l

21

(1.2)(.20) = .24

r

.85

M = ar

l

02

i

.07

.02

.18

.14

La = 0.63 m2 1Z.M = 0.43 m31

As noted previously, the total weight of the pier is

W = (0.63 m2)(0.80 m)(2300 kgf/m3) = 1200 kgf

and the distance this force acts frnrn the origin is

b = \‘M/Sa = (0.43 m2)/(0.63 m) = 0.68 m

The illustration above shows the forces acting on the

pier which the foundation must support: the weight of

the support pier itself acting at 0.68 m from the origin

and the two forces arising from the penstock.

The forces can now be reduced by first resolving them

into x and z components using trigonometric functions.

The algebraic sign is determined by whether the com-

ponent is directed in the positive or negative axis

direction.

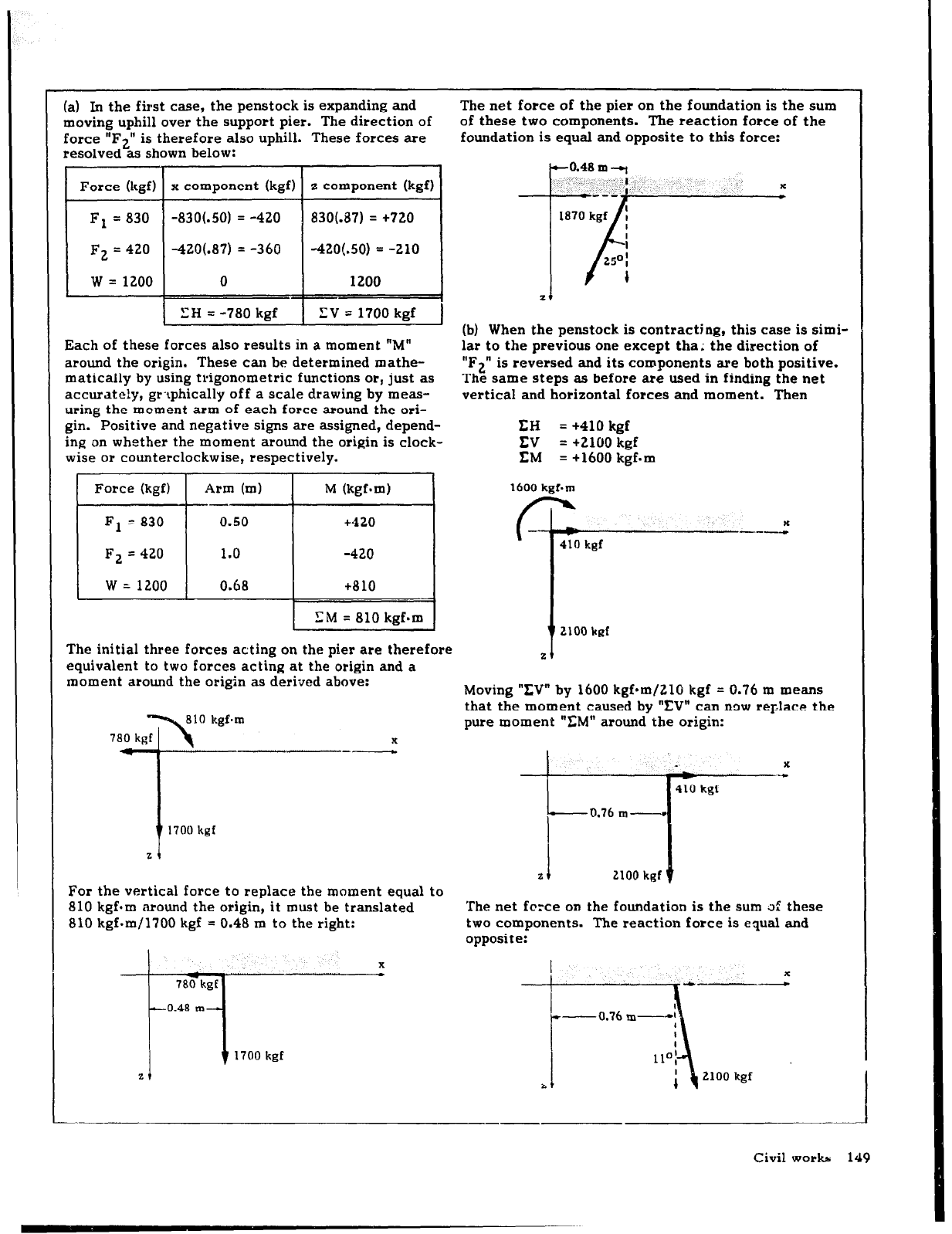
.) In the first case, the penstock is expanding and

oving uphill over the support pier. The direction of

rrce “F2”

is therefore also uphill. These forces are

tsolved as shown below:

The net force of the pier on the foundation is the sum

of these two components. The reaction force of the

foundation is equal and opposite to this force:

Force (kgf) x component (kgf) z component (kgf)

Fl = 830

-830(.50) = -420

830(.87) = +720

F2 = 420 -420(.87) = -360

-420(.50) = -210

w = 1200

0

1200

LH = -780 kgf XV = 1700 kgf

ach of these forces also results in a moment “M”

round the origin. These can be determined mathe-

latically by using trigonometric functions ot, just as

ccurate!y, gt-tphically off a scale drawing by meas-

ring the moment arm of each force around the ori-

in. Positive and negative signs are assigned, depend-

~g on whether the moment around the origin is clock-

(b) When the penstock is contracting, this case is simi-

lar to the previous one except tha; the direction of

“F2” is reversed and its components are both positive.

The same steps as before ate used in finding the net

vertical and horizontal forces and moment. Then

zt

EH

= +410 kgf

EV = +2100 kef

&e ot counterclockwise, respectively.

-

EM = +1600 kgf=m

botce (kgf) [

Arm (ml 1

M

(kgf.m)

F1 = 830

0.50

F2 = 420

1.0

w = 1200

0.68

t420

-420

t810

SM = 810 kgf.m

‘he initial three forces acting on the pier ate therefore

quivalent to two forces acting at the origin and a

lament around the otigin as derived above:

x

---

yor the vertical force to replace the moment equal to

110 kgfom <around the origin, it must be translated

;lO kgf.m/1700 kgf = 0.48 m to the right:

161

410

kgf

Moving “XV” by 1600 kgf*m/ZlO kgf = 0.76 m means

that the moment caused by “IN” can now replace the

pure moment “CM” around the origin:

x

a

410 kg1

I

0.76 m-----r

2 I 2100

kgf 0

The net fcrce

on

the foundation is the sum 3: these

two components. The reaction force is equal and

opposite:

I

x

-0.76 m-1

--

I

Civil works 149

Inversin R. Allen Micro-hydropower Sourcebook

Подождите немного. Документ загружается.