Jones M., Fleming S.A. Organic Chemistry

Подождите немного. Документ загружается.

13.4 The Molecular Orbital Picture of Benzene 579

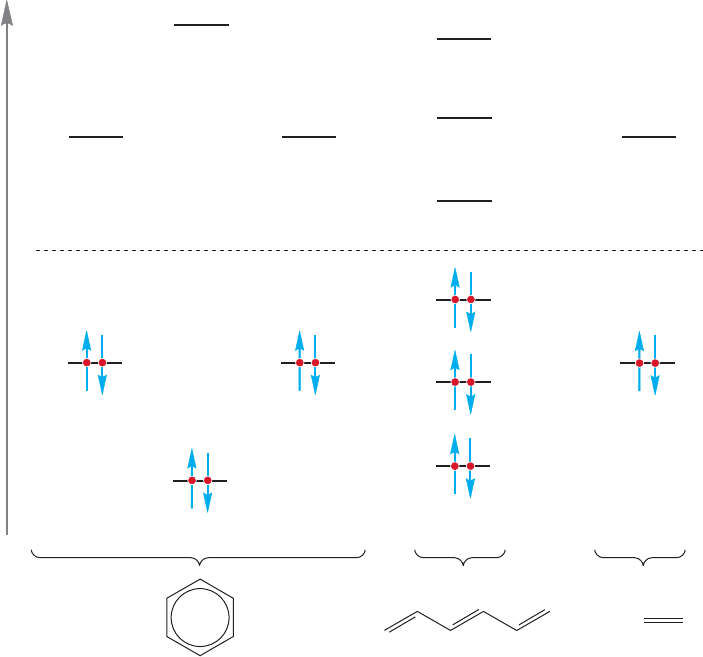
One can calculate the energy difference in terms of a quantity (β) whose value is

approximately −18 kcal/mol (Fig. 13.11). If we sum all the energies of the elec-

trons in Figure 13.11, we find an advantage for benzene over 1,3,5-hexatriene

of 1β. The energetic advantage over three separated ethylenes is even greater: 2β

(Fig. 13.11).

Energy in β

1β

2β

1β

0.45β

1.25β

1.8β

1β

Nonbonding

Benzene Three ethylenes1,3,5-Hexatriene

2  2

β = 4β

4  1β = 4β

––––––––––

2  0.45β = 0.9β

2  1.25β = 2.5β

2  1.80β = 3.6β

––––––––––––––

7.0

2  1β = 2β

for 3 molecules = 6β

FIGURE 13.11 A comparison of the total π energy of benzene, 1,3,5-hexatriene, and

three ethylenes.The calculations are based on the number of electrons and the energy of

each π electron.

Look carefully at how well the orbitals are used in benzene. There is maximum

occupancy of bonding molecular orbitals and no electrons are placed in destructive

antibonding molecular orbitals or wasted in nonbonding molecular orbitals. The

molecular orbital picture gives a stronger hint of the special stability of benzene than

does the resonance formulation.The stability comes not from a large number of res-

onance contributors, but from an especially good, especially low-energy, set of

orbitals. We will soon see other examples. Now the question is: Just how good is

this electronic arrangement? How much more stable is benzene than we might have

expected from a cyclohexatriene model?

580 CHAPTER 13 Conjugation and Aromaticity

13.5 Quantitative Evaluations of Resonance

Stabilization in Benzene

Although we can appreciate that delocalization of electrons is an energy-lowering

phenomenon, it is not easy to see intuitively whether this effect is big or small. In

this section, we see two experimental procedures for determining the magnitude of

resonance stabilization.

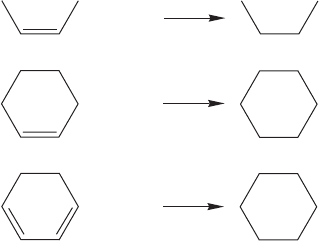
13.5a Heats of Hydrogenation The heat of hydrogenation of cis-2-butene

is 28.6 kcal/mol (Table 10.1, p. 413). There is no change induced by incorpo-

rating the double bond into a six-membered ring, as the heat of hydrogenation of

cyclohexene is also 28.6 kcal/mol (Fig. 13.12). A reasonable guess about the heat

of hydrogenation of a compound containing two double bonds in a ring would

be twice the value for cyclohexene, or 2 28.6 57.2 kcal/mol.This guess is

very close to being correct; the heat of hydrogenation of 1,3-cyclohexadiene is

55.4 kcal/mol. There is no special effect apparent from confining two double

bonds in a six-membered ring. The difference between the observed heat of

hydrogenation for 1,3-cyclohexadiene (55.4 kcal/mol) and the predicted value

(57.2 kcal/mol) is approximately what one would expect, because our prediction

takes no account of the stabilizing effects of conjugation in 1,3-cyclohexadiene

(p. 522).

ΔH = –28.6 kcal/mol

+ H

+ 2 H

ΔH = –28.6 kcal/mol

Estimate: 2  –28.6

ΔH = – 57.2 kcal/mol

Actual:

ΔH = – 55.4 kcal/mol

FIGURE 13.12 Heats of hydrogenation for some alkenes

and cycloalkenes.

Now let’s estimate the heat of hydrogenation for 1,3,5-cyclohexatriene, the

hypothetical molecule with three double bonds in a six-membered ring.We might

make this estimate by assuming that the third double bond will increase the heat

of hydrogenation of 1,3-cyclohexadiene by as much as the addition of a second dou-

ble bond did for cyclohexene [55.4  (28.6) 26.8 kcal/mol]. This incre-

ment would give a predicted value of 55.4  (26.8) 82.2 kcal/mol for the

heat of hydrogenation of the hypothetical 1,3,5-cyclohexatriene. Now we can

measure the heat of hydrogenation of the real molecule, benzene. Hydrogenation

is extremely slow under normal circumstances but there are special catalysts that

can speed the reaction up a bit, and eventually even the stable benzene will hydro-

genate to give cyclohexane. You will learn about these catalysts in Chapter 14.

The important point is that the measured heat of hydrogenation for benzene,

49.3 kcal/mol, is much lower than the calculated value for 1,3,5-cyclohexatriene.

13.5 Quantitative Evaluations of Resonance Stabilization in Benzene 581

Energy

ΔH = –28.6 kcal/mol

ΔH = – 82.2 kcal/mol

estimated for hypothetical

1,3,5-cyclohexatriene

+ 3 H

+ 2 H

+ H

ΔH = –55.4 kcal/mol

Experimental effect

of adding one double

bond (–26.8 kcal/mol)

Predicted effect of adding

one more double bond

(–82.2 kcal/mol)

ΔH = –49.3 kcal/mol

measured for the

real benzene

Energy of

cyclohexane

–32.9 kcal/mol

delocalization energy

of benzene

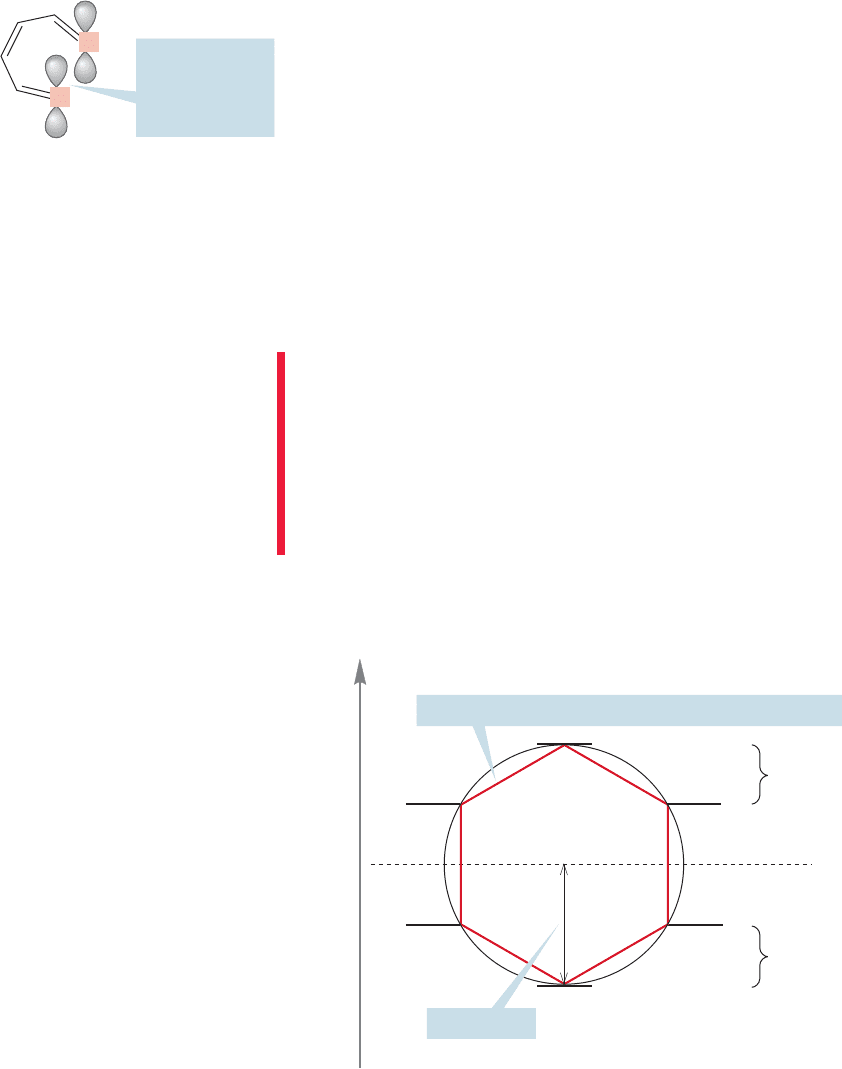
FIGURE 13.13 The value for the special stability of benzene (red arrow) as derived from

measured and calculated heats of hydrogenation. The 1,3,5-cyclohexatriene is drawn with

exaggerated bond lengths.

Figure 13.13 combines all these numbers and shows graphically how this proce-

dure yields the amount by which benzene is more stable than the hypothetical

1,3,5-cyclohexatriene, 32.9 kcal/mol (Fig. 13.13). This difference represents

the amount of energy the special stabilization of benzene is worth. It is more

than 30 kcal/mol and is called the resonance energy or delocalization energy

of benzene.

Summary

We calculated the heat of hydrogenation of the unreal, unknown, hypothetical

molecule 1,3,5-cyclohexatriene by using values for the heats of hydrogenation of

the real molecules cyclohexene and 1,3-cyclohexadiene.The heat of hydrogena-

tion of 1,3-cyclohexadiene was calculated quite accurately, so we can be rather

confident that our estimate for 1,3,5-cyclohexatriene won’t be far off. That’s

important, because we can never make the cyclic triene to check the calculation.

Any synthetic route will inevitably produce the much more stable real molecule,

benzene. The heat of hydrogenation for the real molecule, benzene, is far lower

than our estimate.

13.5b Heats of Formation The delocalization energy of benzene can be

estimated in another way, using heats of formation (ΔH

°). The chemistry of

1,3,5,7-cyclooctatetraene tells us there is no special stabilization in this mol-

ecule. Hydrogenation is fast and addition reactions occur with ease. The ΔH

for cyclooctatetraene is 71.23 kcal/mol, or 8.9 kcal/mol per CH unit.

582 CHAPTER 13 Conjugation and Aromaticity

VANILLIN

Vanillin

Vanilla beans

OCH

CHO

Eugenol

seed pods of the vanilla orchid, Vanilla fragrens.

It appears as well in many other natural sources found in

the tropical world. It is now made synthetically from

eugenol, which, itself has a pleasant clove-like smell.

The term “aromatic” was coined because many such

compounds were odoriferous. Vanillin is a good example,

although there are a great many more. Vanillin is found

in nature attached to a sugar molecule, glucose, in the

ΔH ⬚

= +71.23 kcal/mol

8.9 kcal/mol per CH unit

ΔH ⬚

= +19.82 kcal/mol

3.3 kcal/mol per CH unit

⫻ (8.9 – 3.3) = 33.6 kcal/mol delocalization energy—this value compares

well with that calculated from heat of hydrogenation data (32.9 kcal/mol)

FIGURE 13.14 The delocalization

energy of benzene as calculated from

heats of formation.

The ΔH

° for benzene is 19.82 kcal/mol, or 3.3 kcal/mol per CH unit (Fig. 13.14).

Therefore, benzene is about 5.6 kcal/mol more stable per CH unit than a cyclic poly-

ene with no special stability (8.9  3.3  5.6 kcal/mol). Because there are six CH

units in benzene we can estimate the special stability (resonance or delocalization

energy) to be 6  5.6  33.6 kcal/mol. Note that the two methods, which use the

related heats of hydrogenation and heats of formation, are in rather good agreement.

This special stability has come to be known as benzene’s aromatic character or

aromaticity, a name derived in an obvious way from the pleasant (?) odor of many

benzene derivatives. In the next few pages, we will expand on the theme of aromaticity,

eventually ending up with a general method for identifying aromatic compounds.

13.6 A Generalization of Aromaticity:

Hückel’s 4n ⴙ 2 Rule

It would certainly be surprising if there were not other compounds sharing the spe-

cial stability we have just called aromaticity. To begin our search for other aromatic

compounds,and, ultimately,for a general way of finding such compounds,let’s review

the structural features of the prototype, benzene, that lead to special stability.

13.6 A Generalization of Aromaticity: Hückel’s 4

ⴙ 2 Rule 583

1,3,5-Cycloheptatriene

2p Orbital connectivity

at C(7) broken here by the

group (no 2p orbital)

WEB 3D

FIGURE 13.15 In 1,3,5-

cycloheptatriene, 2p orbital

connectivity is broken by the CH

group. This molecule does not have

benzene’s aromaticity.

1. The molecule is cyclic.Aromaticity is a property of ring compounds. Recall the dis-

cussion of the difference between the molecular orbitals for the cyclic molecule,

benzene, and the acyclic molecule, 1,3,5-hexatriene (Fig. 13.11).

2. The molecule is fully conjugated, which simply means that there is a 2p orbital on

every atom in the ring, and that connectivity between adjacent 2p orbitals is main-

tained throughout. 1,3,5-Cycloheptatriene, for instance, is not aromatic, because

the 2p orbitals of the complete cycle do not overlap. Its properties resemble those

of the acyclic 1,3,5-hexatriene (Fig. 13.15).

If the shape of the molecule uncouples the 2p

orbitals, the molecule is effectively unconjugated

The tub-shaped

cyclooctatetraene

is an example of

this decoupling

phenomenon

Poor 2p connectivity here

FIGURE 13.16 The nonplanar

cyclooctatetraene is not aromatic.

A most unstable molecule, even

though it is planar, cyclic, and

fully conjugated

FIGURE 13.17 Cyclobutadiene is

cyclic, planar, and fully conjugated,

but it is not aromatic and it is very

unstable.

3. The molecule is planar. Why should this make a difference? It ensures optimal

overlap of the 2p orbitals. If the ring is not planar, or at least quite close to planar,

the 2p orbitals do not overlap well and some connectivity between orbitals is lost.

Large deviations from planarity can nearly or completely uncouple the cycle of

orbitals. An example is the tub-shaped molecule cyclooctatetraene (Fig. 13.16).

One might now be tempted to try a generalization. Might not all molecules that are

cyclic, planar, and fully conjugated share benzene’s aromatic character and stability?

Apparently not. Recall from Figure 13.3 that cyclobutadiene, a molecule that meets

all three criteria mentioned above, is most unstable (Fig. 13.17).

There must be more to it, and in our search for further criteria, we must take

into account the difference between benzene and cyclobutadiene. The crucial gen-

eralization was made by the German Erich Hückel (1896–1980) in the early 1930s.

His observation can be added to our previous list of three criteria (also recognized

by Hückel). It is called Hückel’s rule:

4. Aromatic systems will contain 4n  2 π electrons, where n is an integer, 0, 1, 2,

3,...Please note carefully that “n” has nothing to do with the number of atoms in the

ring. We will now discuss the significance of “n.”

We are now faced with the most important question of this section: Why should

the number of π electrons make a difference? Why does Hückel’s rule work? Briefly

stated,it works because it is only those molecules containing 4n  2 π electrons (and

satisfying the other three criteria for aromaticity) that will have molecular orbitals

arranged like those of benzene.These molecules will have a single orbital at the low-

est energy and equal energy pairs of orbitals above it. Orbitals that are equal in ener-

gy are called degenerate. When the lowest molecular orbital and all the bonding

degenerate pair(s) above it are filled, the molecule is aromatic. In “4n  2”, the “2”

is that lowest molecular orbital, and the “4n”refers to the electrons filling the degen-

erate pairs. The value of n is simply the number of filled degenerate pairs. An aro-

matic molecule is stable as a result of the filled molecular orbital system much as

the noble gases are stable as a result of their filled shells. It’s best to look at some

examples now.

cis-1,3,5-Hexatriene can serve as an example for all acyclic molecules. Although

it is fully conjugated (a 2p orbital on every carbon), and can be planar without induc-

ing great strain, it most certainly is not cyclic. The lack of a ring means that there

is no chance of strong overlap between the 2p orbitals on C(1) and C(6) and, there-

fore,no chance of aromatic character (Fig. 13.18).1,3,5-Cycloheptatriene,which we

saw in Figure 13.15, is a cyclic molecule that is not fully conjugated. The connec-

tivity of the 2p orbitals is broken by the methylene group at C(7). This molecule

cannot be aromatic. Cyclobutadiene is a planar, cyclic molecule that is fully conju-

gated. It fails only the fourth criterion because it has 4 π electrons, not a “Hückel

number” of 4n  2.

Before we can go on,we need a reliable way of finding the molecular orbital pat-

terns for these molecules. Consider the device called a Frost circle. It is named for

the American Arthur A. Frost (1909–2002) who devised it in 1953. It is a method

of finding, mercifully without the use of mathematics, the relative energies of the

molecular orbitals for planar,cyclic,fully conjugated molecules. One merely inscribes

a regular polygon, having the same number of sides as the cyclic molecule, into a

circle of radius 2β, vertex down, and the intersections of the ring with the circle will

mark the positions of the molecular orbitals.

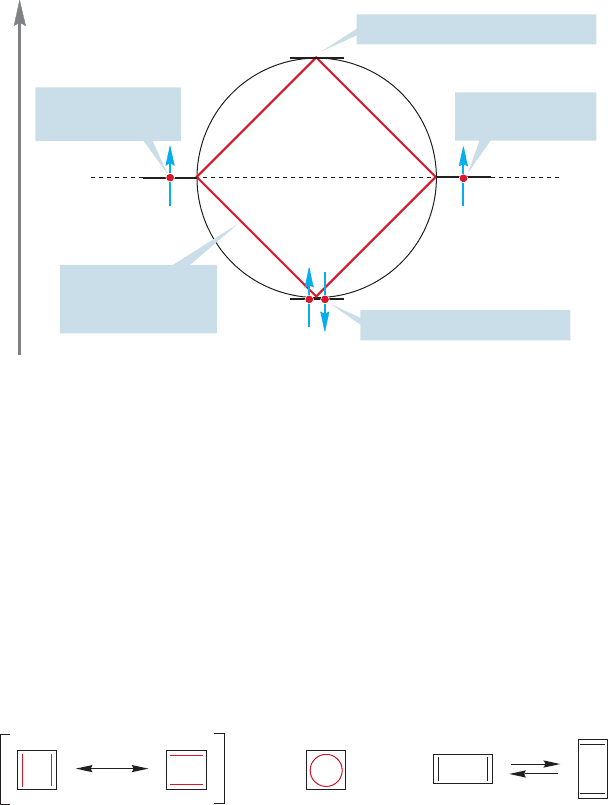
For example, to locate the molecular orbitals of benzene, inscribe a hexagon in

a circle, vertex down as shown in Figure 13.19, with the nonbonding line dividing

the circle exactly in half.

584 CHAPTER 13 Conjugation and Aromaticity

Energy

1β

2β

1β

Hexagon inscribed inside the Frost circle, vertex down

Radius = 2β

Three antibonding orbitals

Three bonding orbitals

will hold the six available

π electrons

Nonbonding

FIGURE 13.19 The relative energies

of the molecular orbitals of benzene

derived from a Frost circle.

No strong

overlap here;

the molecule is

not aromatic

cis-1,3,5-Hexatriene

FIGURE 13.18 cis-1,3,5-Hexatriene is

fully conjugated and can be planar,

but the lack of a ring structure means

that overlap between the 2p orbitals

on C(1) and C(6) is essentially zero.

CONVENTION ALERT

13.6 A Generalization of Aromaticity: Hückel’s 4

ⴙ 2 Rule 585

Energy

A square inscribed

in a circle

(vertex down)

Nonbonding

molecular orbital

Antibonding molecular orbital

Nonbonding

molecular orbital

Bonding molecular orbital

FIGURE 13.20 The relative energies

of the molecular orbitals of cyclobu-

tadiene derived from a Frost circle.

Electrons have been added to this

construct after the energies of the

orbitals have been determined.

Square, delocalized cyclobutadiene, not observed

Rectangular

cyclobutadiene

FIGURE 13.21 In rectangular

cyclobutadiene, shown here with

bond lengths exaggerated, the orbital

connectivity is minimized. Square

cyclobutadiene has never been

observed.

The familiar (p. 578) arrangement of molecular orbitals appears, and with some

plane geometry we can accurately get the energies of the molecular orbitals in terms

of β. For benzene, the available six π electrons completely fill the three available

bonding molecular orbitals with no offending electrons remaining to be placed in

the antibonding set. There are no nonbonding molecular orbitals. Most important,

the degenerate pair of bonding orbitals is filled.

If we follow this procedure for cyclobutadiene, a set of four molecular orbitals

appears (Fig. 13.20). One is bonding, one is antibonding, and two are degenerate,

nonbonding molecular orbitals. Four π electrons are available and two of them will

surely go into the bonding molecular orbital.The remaining two electrons will have

to occupy the nonbonding degenerate pair, and will be most stable in this square

arrangement if the spins are unpaired and a single electron is put into each orbital

of the pair (Fig. 13.20). This arrangement is surely not particularly stable, and we

would not expect the properties of cyclobutadiene to resemble those of benzene, as

they most emphatically do not. It is also true that cyclobutadiene must pay a price

in ring strain as the internal angles are constrained at 90° but “want to be” 120°.

But it is not this strain that makes cyclobutadiene so especially unstable.There are

many compounds with considerable ring strain that are isolable and stable at room

temperature. Its instability is due to the fact that it has 4n π electrons. The degen-

erate orbitals have a single electron each, essentially making square cyclobutadiene

a diradical species. Remember from Chapter 11 that radicals are very reactive.

Cyclobutadiene can be isolated and observed at very low temperatures (its IR spec-

trum was measured at 8 K 265 °C), as long as it is segregated from other reac-

tive molecules, including itself. Theory and experiment agree that cyclobutadiene

distorts from the square arrangement to form a rectangle with short carbon–carbon

double bonds and longer carbon–carbon single bonds. This distortion to a rectan-

gle minimizes the conjugation of the p orbitals (Fig. 13.21).

Energy

17 kcal/mol

FIGURE 13.24 The tub-shaped

cyclooctatetraene is 17 kcal/mol more

stable than the planar, delocalized

structure.

586 CHAPTER 13 Conjugation and Aromaticity

Energy

Antibonding

molecular

orbitals

Bonding

molecular

orbitals

An octagon inscribed

in a circle (vertex down)

Nonbonding

molecular orbital

Nonbonding

molecular

orbital

FIGURE 13.22 The molecular orbitals

of planar cyclooctatetraene. Because

there are eight π electrons, two must

occupy nonbonding orbitals.

Angle strain

relieved 126°

(calculated)

Angle strain 135°

FIGURE 13.23 In planar

cyclooctatetraene, there is both

angle strain and diradical reactivity.

Both can be avoided by distorting

into a tub shape.

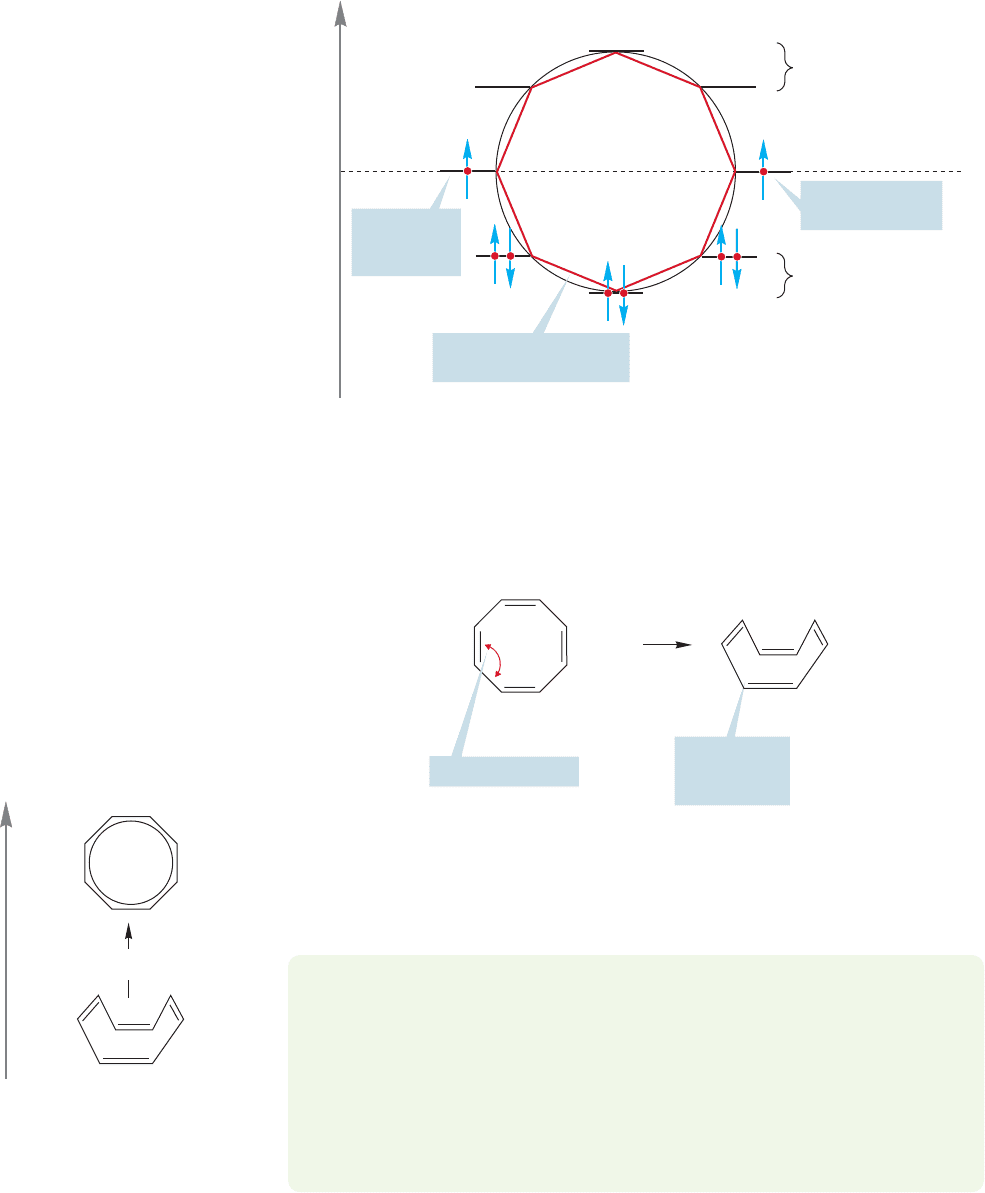
1,3,5,7-Cyclooctatetraene is another example of a 4n molecule.But here we find

neither the special stability of benzene,nor the special instability of cyclobutadiene.

The molecule behaves like four separated, normal alkenes. Let’s first examine pla-

nar cyclooctatetraene.The Frost circle again determines the relative positions of the

molecular orbitals (Fig. 13.22).

Like cyclobutadiene, planar cyclooctatetraene must have one electron in each of

the degenerate nonbonding molecular orbitals, making it a diradical. Unlike cyclobu-

tadiene, however, there is a way for cyclooctatetraene to get out of its energetic mis-

ery. Cyclobutadiene must be planar, or very nearly so. By contrast, cyclooctatetraene

can distort easily into a tublike form in which most of the angle strain and the dirad-

ical nature of the planar form is avoided (Fig. 13.23).

Kinetic measurements reveal that the energy difference between the tub and the

planar, delocalized species is 17 kcal/mol. The tub is more stable than the planar,

symmetrical, fully conjugated octagon (Fig. 13.24). This example is a rare case of

conjugation being avoided because it destabilizes the molecule.

PROBLEM 13.6 The interconversion of cyclooctatetraene forms is a bit more compli-

cated.There are actually two tub forms that interconvert rather easily.The two local-

ized tubs (alternating single and double bonds, not conjugated) equilibrate without

the double bonds changing position. The activation energy for this process is

14.6 kcal/mol. The conversion into the planar, delocalized form requires an addi-

tional 2.4 kcal/mol. Neither the localized planar form nor the delocalized planar

form is an energy minimum. In other words, they can’t be isolated. Based on this

information, sketch an Energy versus Reaction progress diagram for these processes.

PROBLEM 13.7 Which of the following molecules are properly termed “aromatic”

and which are not? For those that are not, explain why not.

13.6 A Generalization of Aromaticity: Hückel’s 4

ⴙ 2 Rule 587

(a)

(b)

(c)

WEB 3D

(d)

(e)

1,3,5-Cycloheptatriene

(tropilidine)

–

Trityl cation TriphenylmethaneTropylium

fluoborate

–

FIGURE 13.25 The tropylium ion (C



) can be made through transfer of hydride ( )

from 1,3,5-cycloheptatriene to the trityl cation.

We have now discussed the lack of aromaticity in 4n molecules and we have

seen a few examples of aromaticity (benzene and some of the molecules in Problem

13.7); it would seem to be time to look at some other potentially aromatic 4n  2

molecules. It is in the stability of certain ions that the most spectacular examples

have appeared.As we have stressed over and over, small carbocations are most unsta-

ble. But there are a few exceptions to this generality. One of them is the cyclohep-

tatrienylium ion, or tropylium ion (C



), the ion derived from the loss of

hydride ( ) from 1,3,5-cycloheptatriene, also called tropilidene (Fig. 13.25).

Hydride cannot be simply lost from cycloheptatriene, but it can be transferred to

the trityl cation, a carbocation attached to three benzenes, which is itself a quite

stable carbocation.

Tropylium fluoborate appears to be stable indefinitely under normal conditions.

It sits uncomplaining on the desktop, for all the world resembling table salt. This

stuff is no ordinary carbocation!

PROBLEM 13.8 Why is the trityl cation relatively stable?

588 CHAPTER 13 Conjugation and Aromaticity

Energy

Nonbonding

Tropylium ion

Benzene

Antibonding

molecular

orbitals

Bonding

molecular

orbitals

A heptagon inscribed in a circle (vertex down)

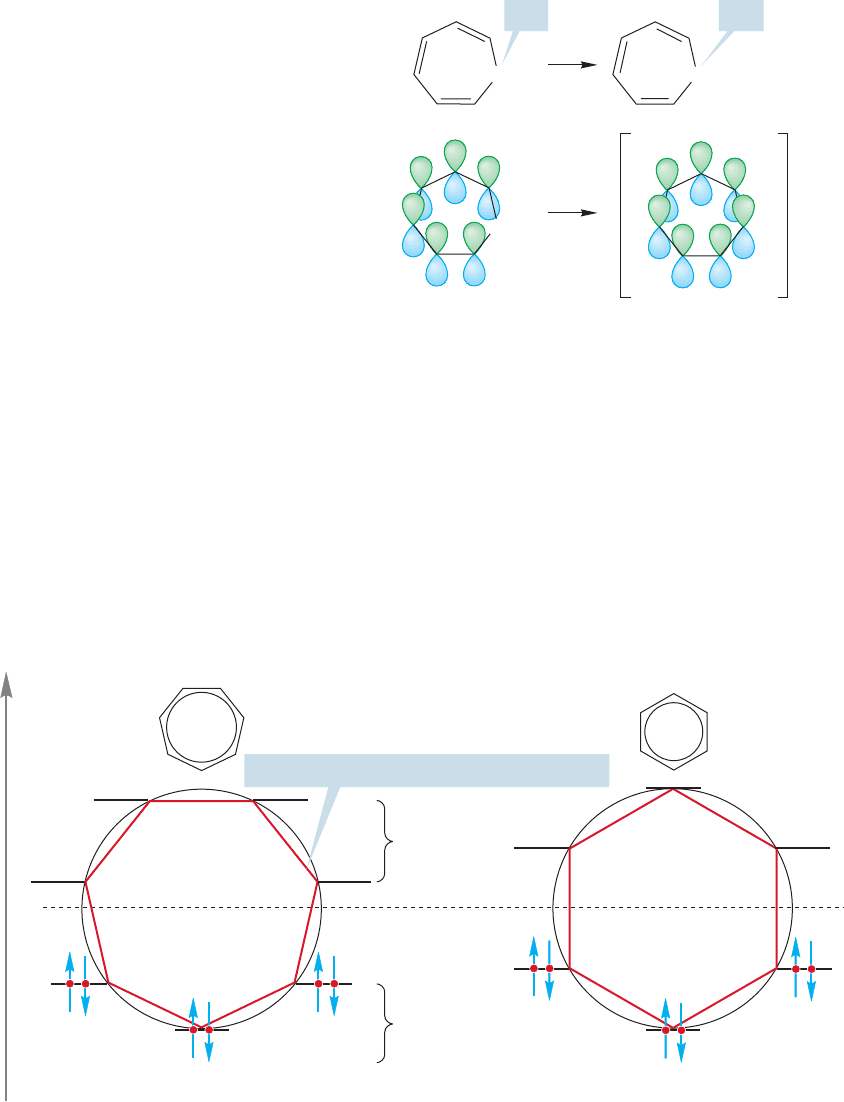
FIGURE 13.27 In the tropylium ion, the lowest single orbital and the bonding degenerate molecular orbitals are fully occupied.

The molecular orbital picture of the tropylium ion closely resembles that of benzene.

The cycloheptatrienylium

(tropylium) ion is fully conjugated

1,3,5-Cycloheptatriene is

not fully conjugated

C(7) C(7)

FIGURE 13.26 In the tropylium ion

(the cycloheptatrienylium ion)

orbital connectivity is continuous

around the ring.

Note first that the tropylium ion has one important difference from its parent,

1,3,5-cycloheptatriene. The ion is fully conjugated (Fig. 13.26). The removal of a

hydride from the cyclic triene generates a 2p orbital at the 7-position, which once

insulated the two ends of the π system from each other. In the cation they are now

connected and this molecule is fully conjugated.

The Frost circle analysis lets us see the relative energies of the molecular orbitals

for this system (Fig. 13.27). Notice the degenerate pairs of orbitals. How many elec-

trons must go into the π system? In the cation, there is an empty 2p orbital on C(7)

and the only π electrons are the six from the three original double bonds. These elec-

trons can fit nicely into the three bonding molecular orbitals of the π system.Note how

this system resembles the arrangement of benzene—the occupied degenerate molec-

ular orbitals are full (Fig. 13.27).This ion qualifies as aromatic, and the increased sta-

bility relative to other carbocations is dramatic indeed. Notice that the number of atoms

involved in the ring—here seven—is independent of the number of π electrons—here