Jones M., Fleming S.A. Organic Chemistry

Подождите немного. Документ загружается.

15.6 NMR Measurements 719

In this spectrum, the assignment is easy; the nine hydrogens of the tert-butyl

group give rise to a signal around δ 1 ppm, the methyl group produces the signal

for three hydrogens, and the methylene group gives the peak for two hydrogens.

From now on, integrations in the figures will often be indicated by a number

followed by H, as in 1H, 2H, and so on.

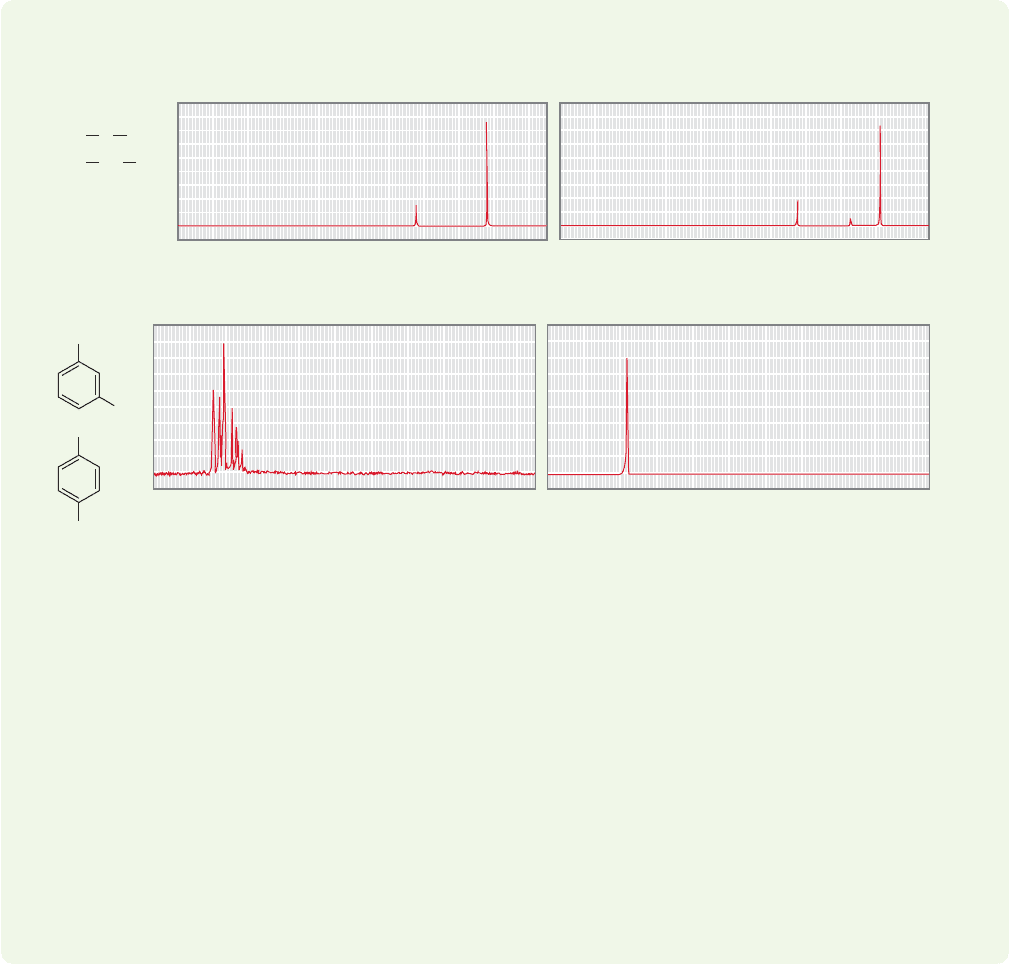
ANSWER (a) First of all, notice that this problem can be solved just by counting

signals. tert-Butyl methyl ether has only two kinds of hydrogen whereas

neopentyl alcohol (2,2-dimethylpropanol) has three. Thus, spectrum A1

belongs to the ether and spectrum A2 belongs to the alcohol. That’s all there is

to it. Why is the ratio of hydrogens in spectrum A1 1:3 not 3:9? Remember that

integration only gives the relative number of hydrogens—it is not an absolute

measure. There are other clues here. A nine-hydrogen signal? That’s certain to

be a tert-butyl group. In spectrum A1 there is a signal at approximately δ  3.3

ppm. That region is something of a desert in

H NMR spectra, and almost

always indicates a hydrogen attached to a carbon that is also attached to an

oxygen.

(b) Here symmetry also allows a quick assignment. 1,4-Dicyanobenzene has only

one kind of hydrogen and must give rise to the spectrum B2. 1,3-Dicyanobenzene

has three different hydrogens and has the far less symmetrical spectrum B1.

109876543210

(ppm)

Chemical shift (δ)

109876543210

(ppm)

Chemical shift (δ)

(b)

3H 9H

Spectrum B1 Spectrum B2

109876543210

(ppm)

Chemical shift (δ)

109876543210

(ppm)

Chemical shift (δ)

(a)

O(CH

)

OHCH

(CH

)

3H 9H

Spectrum A1 Spectrum A2

The examples in Problem 15.10 are straightforward, and are designed to ease

you into analyzing NMR spectra. In no area of organic chemistry is practice so

necessary in the development of skill.You simply cannot become proficient at this

kind of structure determination by reading about how it is done and studying

WORKED PROBLEM 15.10 Which of the molecules below give rise to which

spectra?

15.6b The Chemical Shift We need to know how the dependence of the

chemical shift (δ) on the local environment arises. In a sense, this is a nonquestion.

If two hydrogens are different, they must give different NMR signals. It is in fact

just a question of whether our ability to detect the difference is great

enough, because the difference must be there. Electrons in molecules occu-

py regions of space defined by the molecular orbitals of the molecule. The

chemical shift depends on the local environment because, when an external

magnetic field (B

) is applied, the electrons will circulate within those

regions of space so as to create an induced magnetic field (B

) that opposes

the applied field B

(Fig. 15.23).

The net magnetic field (B

net

 B

 B

) must be slightly different at every

different hydrogen in the molecule,and therefore the resonance frequency will

also be different for every different hydrogen.Relative to the hydrogens in TMS,

for most (not quite all) hydrogens in a sample molecule,the circulation of elec-

trons produces an induced magnetic field that augments the applied magnet-

ic field.The net magnetic field (B

net

) felt by most hydrogens is actually greater

than the applied magnetic field. Such hydrogens are said to be “deshielded”by

the induced field and they appear downfield of TMS, that is, to the left of

TMS, in the NMR spectrum. In a very few instances, we find that hydrogens

are “shielded” and appear upfield of TMS. In these cases, the magnetic field,

,is opposed by the induced field,B

,and it takes less energy to flip the nuclear

720 CHAPTER 15 Analytical Chemistry: Spectroscopy

Table 15.4, which gives approximate values of δ for many kinds of hydrogen.

Working problems is an absolute must. Do the problems at the end of this chapter

and seek out others. Other textbooks have good ones, and NMR problems can also

be found on-line; don’t be reluctant to dig them out.

TABLE 15.4 Chemical Shifts of Various Hydrogens

Hydrogen ␦ (ppm)

(methyl hydrogens) 0.8–1.0

(methylene hydrogens) 1.2–1.5

CH (methine hydrogen) 1.4–1.7

(allylic hydrogens, x  1, 2, or 3) 1.7–2.3

(α to carbonyl hydrogens, x  1, 2, or 3) 2.0–2.7

(benzylic hydrogens, x  1, 2, or 3) 2.3–3.0

(alkynyl hydrogen) 2.5

(α to amine hydrogens, x  1, 2, or 3) 2.0–2.7

(α to iodine, x  1, 2, or 3 ) 3.2

(α to bromine, x  1, 2, or 3) 3.4

(α to chlorine, x  1, 2, or 3) 3.5

(β to chlorine) 1.8

(α to fluorine, x  1, 2, or 3) 4.4

(α to ether or alcohol oxygen, x  1, 2, or 3) 3.2–3.8

(vinylic hydrogens) 4.5–7.5

(aromatic hydrogens) 6.5–8.5

(aldehydic hydrogen) 9.0–10.0

ROH (hydroxyl hydrogens) 1.0–5.5

ArOH (phenolic hydrogens) 4.0–12.0

RNH

(amine hydrogens, x  1 or 2) 0.5–5.0

CONH

(amide hydrogens, x  1 or 2) 5.0–10.0

RCOOH (carboxylic hydrogens) 10–13

These values are approximate. There will surely be examples that lie outside the ranges indicated.

Use them as guidelines, not “etched in stone”inviolable numbers.

(the applied

magnetic field)

(the induced

magnetic field)

A hydrogen

nucleus at this

position “feels”

net

= B

– B

A hydrogen

nucleus at this

position “feels”

net

= B

+ B

Electron

cloud

FIGURE 15.23 In an applied magnetic field

, electrons circulate so as to generate an

induced magnetic field (B

) that opposes

the applied field.

15.6 NMR Measurements 721

spin. Because there are so few molecules that have signals

upfield of TMS, we can set δ for TMS as 0, with the spec-

trum usually appearing entirely to the left of TMS.

We can expect to see a signal for each different hydro-

gen in a molecule,and this idea leads to the another some-

times thorny question, What constitutes different

hydrogens? There is a simple scheme for finding identi-

cal (chemically and magnetically equivalent) hydrogens.

First, carry out mental substitutions of the hydrogens in

question with a phantom group X one at a time. If the

resulting molecules are identical, the hydrogens are also

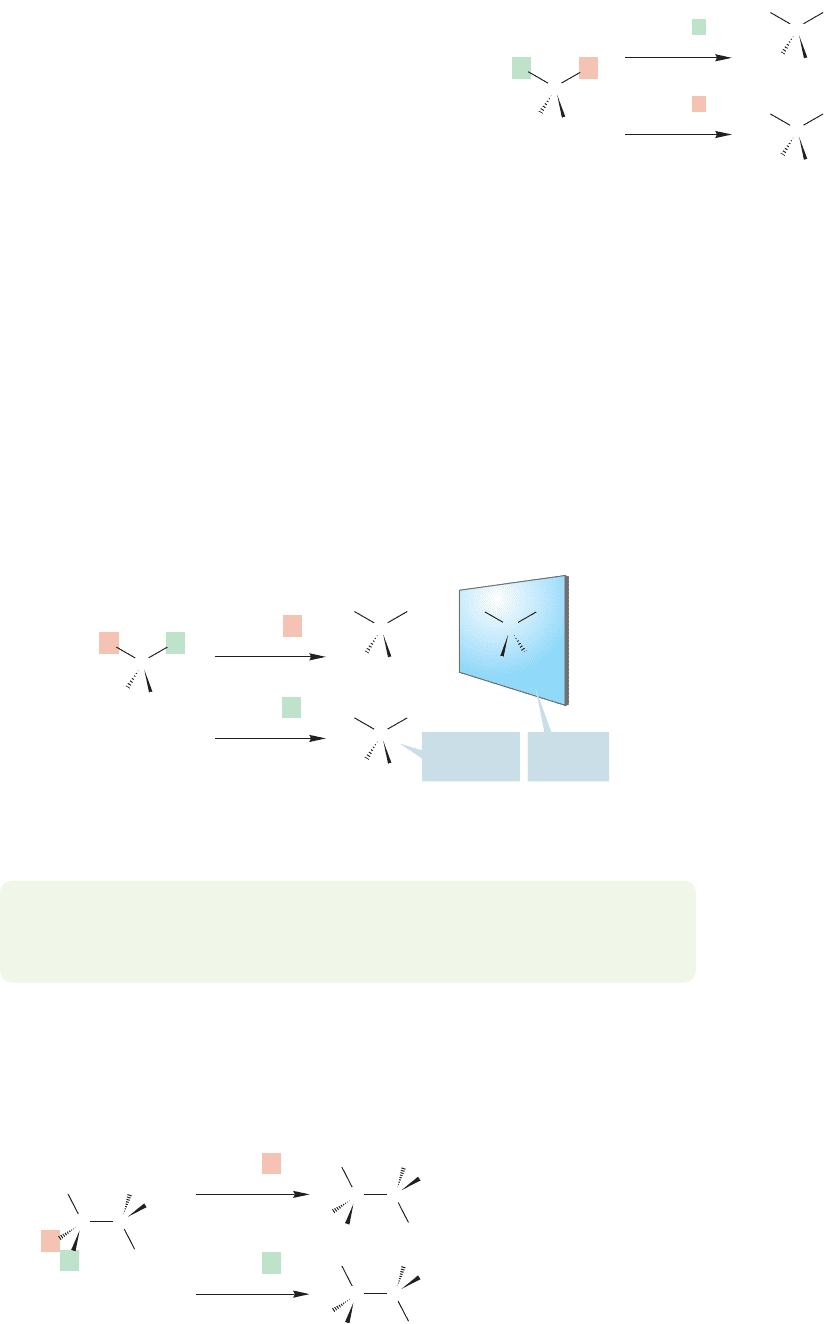
identical, or homotopic. Figure 15.24 gives an example using methylene chloride.

Replacement of either hydrogen (red or green in the figure) with X gives the same

CHCl

X. The two hydrogens of methylene chloride are homotopic and equivalent

in all chemical and spectroscopic operations.

Hydrogens in more complicated molecules are usually not homotopic.

Chlorofluoromethane is a good example. Replacement of the two hydrogens by the

phantom X in this case does not yield identical molecules (Fig. 15.25). The result-

ing compounds are enantiomers.When this mental replacement exercise gives enan-

tiomers, the hydrogens are said to be enantiotopic. Enantiotopic hydrogens are

equivalent in chemical reactions and NMR spectra, as long as chiral reagents or sol-

vents are not involved.

PROBLEM 15.11 Explain why the enantiotopic hydrogens of chlorofluoromethane

will show different signals if the NMR spectrum is obtained with an optically

active additive (often the solvent).

replace H

with X

replace H

with X

These molecules are

identical—the two

hydrogens are

homotopic, or

“NMR equivalent”

FIGURE 15.24 Substituting either of the two hydrogens gives

identical molecules; therefore the hydrogens in methylene

chloride are homotopic. Homotopic hydrogens are equivalent.

Mirror

replace H

with X

replace H

with X

These molecules are enantiomers;

the two hydrogens in chlorofluoro-

methane are enantiotopic

Chlorofluoro-

methane

Slide this

molecule…

…to this

position

FIGURE 15.25 The two molecules

obtained by substituting one of the

two hydrogens are enantiomers;

therefore the hydrogens are

enantiotopic. Enantiotopic hydrogens

are equivalent in typical NMR

experiments.

replace H

with X

replace H

with X

These molecules are

diastereomers; the two

methylene hydrogens are

diastereotopic and not

“NMR equivalent”

1,2-Dichloro-

fluoroethane

FIGURE 15.26 The two molecules

obtained by substituting one of the

two hydrogens are diastereomers;

therefore the hydrogens are

diastereotopic. Diastereotopic

hydrogens are not equivalent in

NMR analysis.

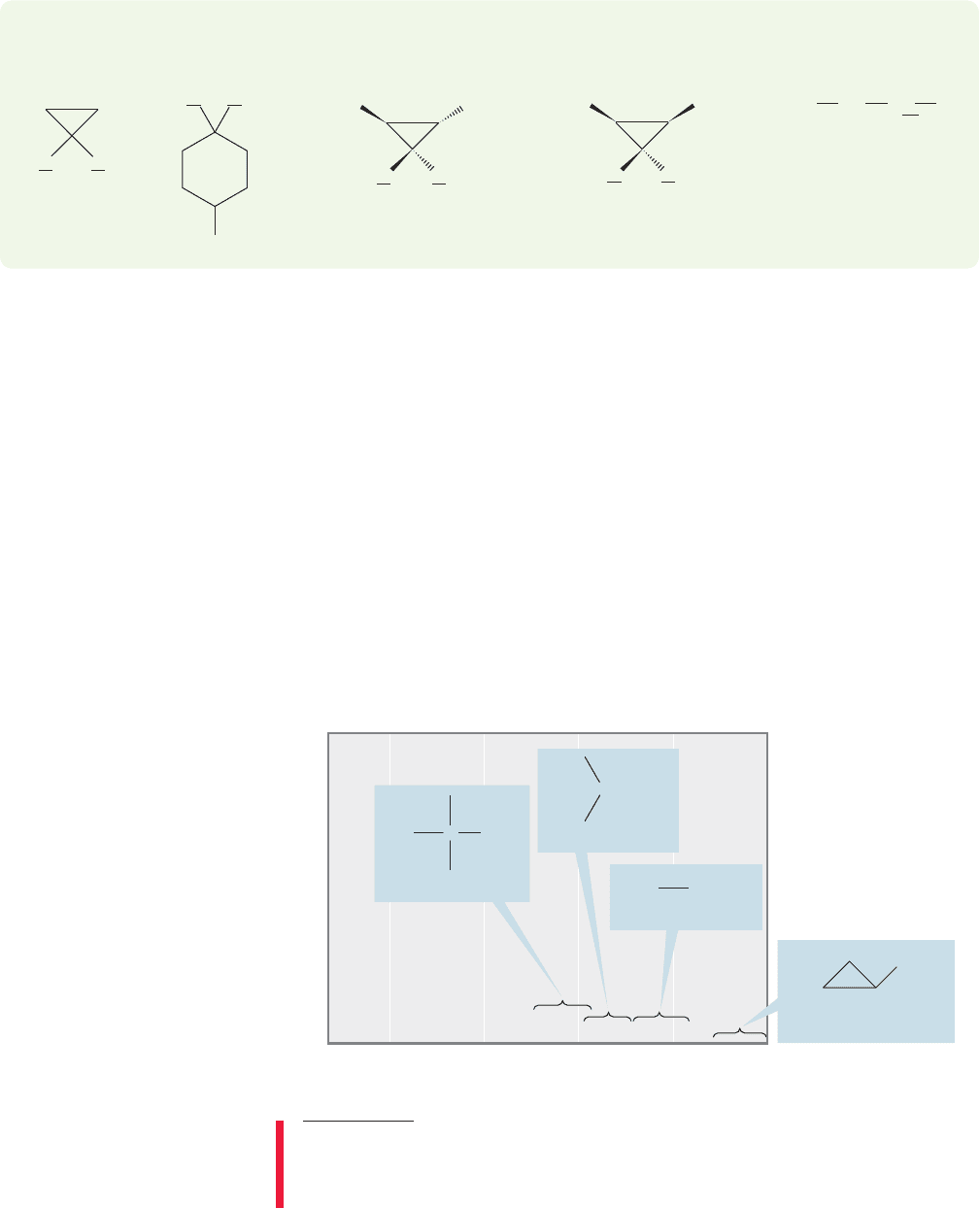
Finally, consider 1,2-dichlorofluoroethane (Fig. 15.26). Now replacement of

the two methylene hydrogens gives neither identical molecules nor enantiomers,

but diastereomers (p. 164). These hydrogens are diastereotopic. Diastereotopic

hydrogens are chemically different and will always give different signals in the NMR

(a) (b)

C(CH

)

(c)

(d) (e)

722 CHAPTER 15 Analytical Chemistry: Spectroscopy

spectrum. Of course, diastereotopic hydrogens can be so similar that the spectrom-

eter cannot resolve the signals. There are many such examples, especially in old

spectra in which low-field spectrometers were used.

Now let’s return to the issue of chemical shifts. There is a general correlation

between the resonance frequency in an NMR spectrum of hydrogens that are in

similar enviroments in different molecules. For example, all methyl groups attached

to double bonds appear at roughly the same position, all aromatic hydrogens at

another, and so on.

Table 15.4 gives a correlation chart for the peak positions of

many different kinds of hydrogen. Use this table when working problems and you

will gradually become familiar with the chemical shifts of commonly encountered

hydrogens. Now we will discuss several of the factors that influence the chemical

shift in more detail.

Alkanes. NMR signals from saturated alkanes (and the simplest cycloalkanes)

are typically the furthest upfield. Because alkane hydrogens are unperturbed by any

substituents, we can think of the region where they appear (around 1 ppm) as a

beginning point. Signals for all organic compounds would appear at about 1 ppm if

there were no functional groups.There are exceptions of course.For example, hydro-

gens on a cyclopropane ring are at unusually high field, sometimes even appearing

upfield (to the right) of TMS (Fig. 15.27). A useful trend for analyzing NMR

2.5 2 1.5 1

(ppm)

Methine

Methyl

Methylene

Cyclopropyl hydrogens

(very high field)

FIGURE 15.27 The

H NMR

chemical shifts of alkanes.

To say “aromatic hydrogen”is certainly wrong; the hydrogen isn’t aromatic, it is the ring to which it is attached

that is. Nonetheless, one must admit that it is slightly awkward to say “hydrogens attached to aromatic sys-

tems,” and this kind of loose talk is common. One refers to vinylic hydrogens, allylic hydrogens, cyclopropyl

hydrogens, for example.

CONVENTION ALERT

PROBLEM 15.12 Identify the underlined hydrogens in each of the following

molecules as homotopic, enantiotopic, or diastereotopic.

15.6 NMR Measurements 723

spectra of alkanes is that in any given environment a methyl group will be about

0.3 ppm upfield from a methylene group and a methylene group will be about 0.3 ppm

upfield of a methine. This trend is the reason why several entries of Table 5.4

have a range of chemical shift values that depends on the number of hydrogens on

the carbon.

Electronegative Groups. Electron-withdrawing groups will reduce the electron

density at neighboring hydrogens through an inductive effect (p.237), which decreas-

es electron-shielding of the nucleus. As a result of this deshielding,the chemical shifts

appear further downfield than those of alkanes.This effect is directly related to the

electronegativity of the substituent. Notice, for example, that because fluorine is

the most electronegative halogen,alkyl fluorides appear furthest downfield of all the

halogen-substituted molecules (Fig. 15.28). Chlorine and oxygen have almost the

same electronegativity and, as a result, the signals for the hydrogens of

and both appear at about 3.5 ppm (Table 5.4).CH

6 5.5 5 4.5 4 3.5 3 2.5 2

1.5

CHCl

CHBr

CHI

CHF

(RO)

CHRO

CHR

(ppm)

X = F X = Cl X = Br X = I

CHX

4.26 3.05

5.31

7.28

2.68

4.96

6.86

2.16

3.88

5.36

3.5 1.4

1.8 0.9

FIGURE 15.28 The

H NMR chemical shifts of alkanes substituted with electron-withdrawing groups.

The effect of electronegative groups is understandably additive. Thus, increas-

ing the number of electronegative groups in the neighborhood of a hydrogen increas-

es the overall electron-withdrawing effect, and the resonance position shifts further

downfield. A clear example of this additivity is the comparison between CH

(δ 3.1 ppm), CH

(δ 5.3 ppm), and CHCl

(δ 7.3 ppm). The chlorine has a

deshielding effect of about 2.2 ppm (remember that unperturbed methyl hydrogens

appear about 0.9 ppm).The effect of the second chlorine in CH

is an addition-

al 2.2 ppm, which produces the observed chemical shift of 5.3 ppm. To predict the

chemical shift of CHCl

, one adds the effect of another chlorine (2.2 ppm), giving

7.5 ppm,which is close to its observed chemical shift of 7.3 ppm.The inductive effect

is also felt to a small extent by the hydrogens on the β carbon. The α carbon is the

carbon that is directly attached to the electronegative group. The hydrogens on the

α carbon are significantly shifted as shown in Table 5.4. The β carbon is attached

to the α carbon (there can be more than one β carbon). The hydrogens on the β

carbon in 1-chlorobutane (see Fig. 15.28) appear at δ 1.8 ppm. If the chlorine were

not present, then the chemical shift would be about 1.3 ppm. So the effect of the

chlorine on the β position is about 0.5 ppm, compared to the 2.2 ppm effect on the

α position. As we move further away from the electronegative group there is little

to no impact on the chemical shift.

724 CHAPTER 15 Analytical Chemistry: Spectroscopy

Allylic Hydrogens. A carbon–carbon double or triple bond is electron-withdrawing,

and therefore exerts a deshielding effect, shifting the signal downfield for hydrogens

in the allylic position. The carbon–oxygen double bond exerts a similar, but greater

effect (Fig. 15.29).

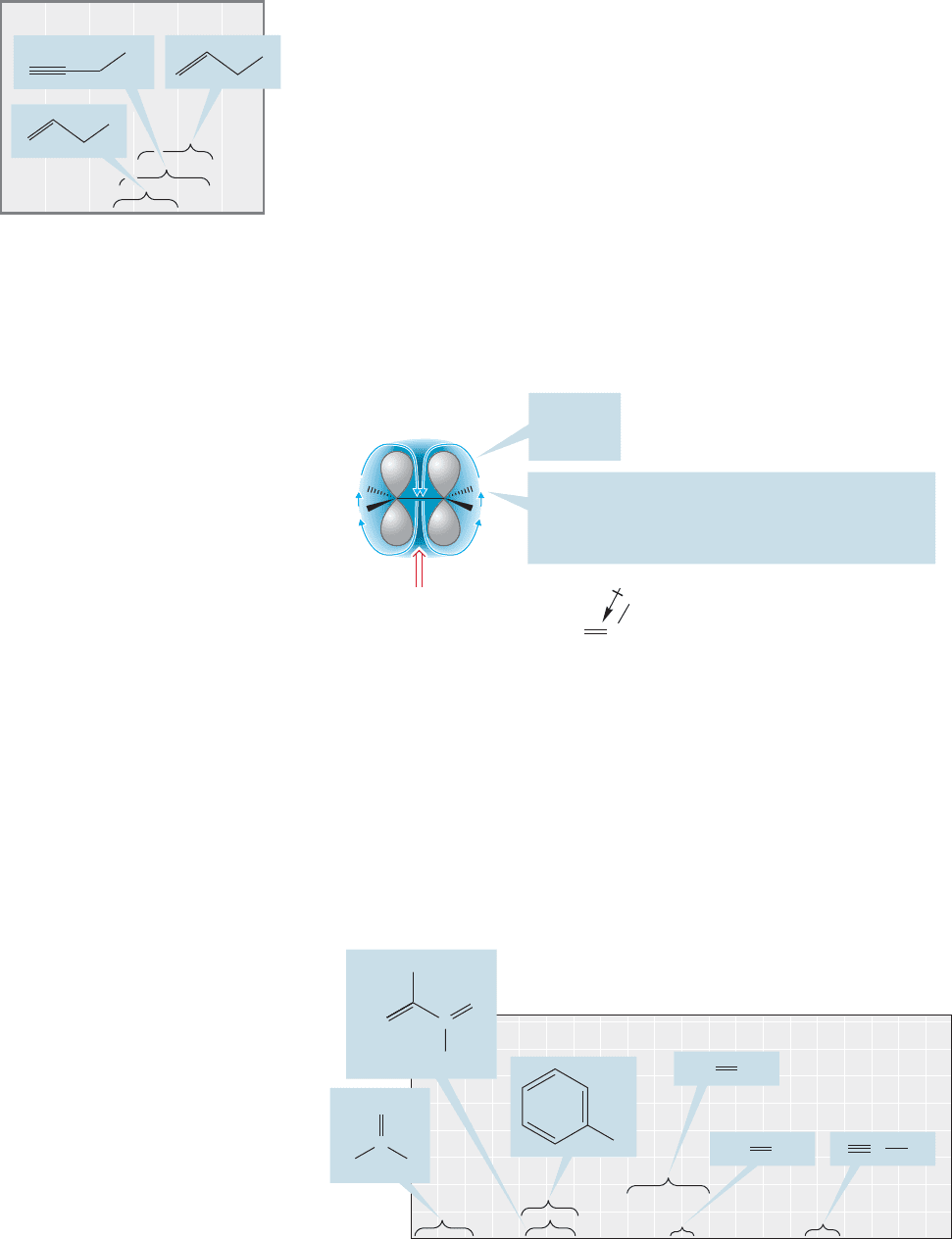
Hybridization. Hydrogens attached directly to a carbon–carbon double bond are

called vinylic hydrogens. Vinylic hydrogens appear downfield from hydrogens on

hybridized carbons. Two effects are operating to deshield such hydrogens and

produce the downfield signals. In an external magnetic field, B

, the electrons in the

π bond will circulate so as to create a magnetic field B

that adds to B

in the region

where the hydrogens reside (Fig. 15.30). In addition, the sp

carbon of the double

bond has high s character and attracts electrons, thereby removing electrons from

the vicinity of the hydrogen and deshielding it. As a result of these two phenome-

na, vinylic hydrogens appear around δ 5.5 ppm.

There are important differences between the various kinds of hydrogens

attached to double bonds. For example, terminal methylene hydrogens appear

further upfield than most vinylic hydrogens the same way that a methylene

group appears upfield of a methine. Based on the hybridization trend, a hydro-

gen directly attached to a triply bonded carbon (alkynyl hydrogen) ought to

have a chemical shift around δ 9 ppm. However, it appears at δ 2.2–2.8, at

substantially higher field than hydrogens attached to double bonds (Fig. 15.31).

The sp

carbon has high

s character and withdraws

electrons, deshielding the

hydrogen

CCH

Induced

magnetic

field, B

At this point, B

is augmented by B

. The hydrogen

will “feel” a net B

net

= B

+ B

, and require a reduced

come into resonance. It appears at relatively

low field (downfield)

FIGURE 15.30 A carbon–carbon

double bond acts in two ways to

deshield attached hydrogens. Such

deshielded hydrogens appear

relatively downfield.

109876

(ppm)

5432

RCH CHR

R = alkyl

R H

FIGURE 15.31 The

H NMR

chemical shifts of alkenes and

alkynes.

4 3.5 3 2.5 2 1.5

(ppm)

FIGURE 15.29 The

H NMR

chemical shifts of hydrogens adjacent

to double and triple bonds.

15.6 NMR Measurements 725

The induced

magnetic

field B

At this point the induced magnetic

field B

opposes the applied field

; a hydrogen here “feels” a net

magnetic field, B

net

= B

– B

. The

alkynyl hydrogen is shielded, and

a relatively high B

will have to be

applied to bring this shielded

hydrogen into resonance

FIGURE 15.32 Acetylenic hydrogens

are strongly shielded by the induced

magnetic field.

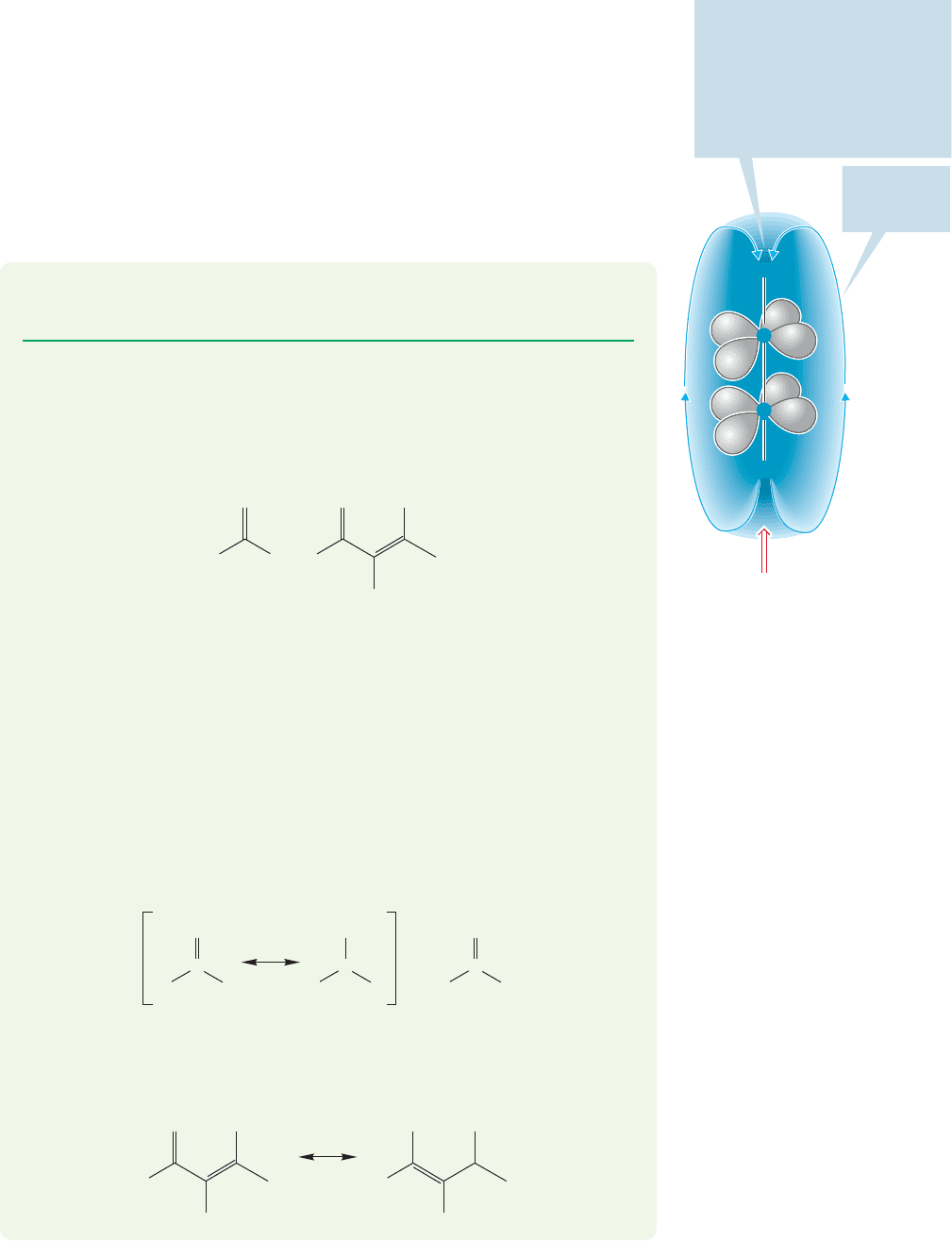
The upfield shift results from a strong shielding effect induced by circulation of

electrons in the triple bond (Fig. 15.32).

Delocalization. Hydrogens attached to a double bond, and β to a carbonyl group,

have a chemical shift surprisingly far downfield, and the hydrogens of aldehydes are

even further to the left (Fig. 15.31). These two examples show the effect that delo-

calization can have on chemical shifts.Groups that withdraw electrons by resonance

significantly deshield hydrogens on carbons at the β position. Alternatively, a

group that can donate electrons by resonance shifts hydrogens on the adjacent

carbon upfield (Problem 15.13). Such hydrogens are the furthest upfield of all

vinylic hydrogens.

R H

(a) (b)

–

ANSWER (a) In the absence of other effects, we would expect to see the hydro-

gen of an aldehyde group at about the position of hydrogens attached to

carbon–carbon double bonds. However, the carbonyl group is very polar. The

oxygen atom is much more electronegative than the carbon and will attract elec-

trons strongly, becoming partially negative (δ



) and leaving the carbon partially

positive (δ



). The same effect can be seen from a resonance formulation. The

electron density around carbon is depleted and the attached hydrogen is the most

deshielded hydrogen in neutral organic molecules. Accordingly, a weaker mag-

netic field is necessary to reach the resonance frequency, and the hydrogen

appears downfield.

(b) Conjugated carbonyl compounds have important resonance forms in which

the β carbon is positively charged. The resulting deshielding leads to an especially

downfield chemical shift for the β hydrogens.

PROBLEM 15.13 Predict the chemical shifts for the hydrogens in methoxyethene

(methyl vinyl ether).

WORKED PROBLEM 15.14 (a) A hydrogen attached directly to the carbon of a car-

bonyl group (aldehyde hydrogen) appears at δ 9–10 ppm, and must be strongly

deshielded. Explain why. (b) Vinylic hydrogens that are on the β position of a

conjugated carbonyl compound are also substantially downfield. Use resonance

structures to explain why.

–3.0

(these negative chemical shifts mean

that the signals are to the right of TMS)

δ –0.5 δ –0.01

WEB 3D

726 CHAPTER 15 Analytical Chemistry: Spectroscopy

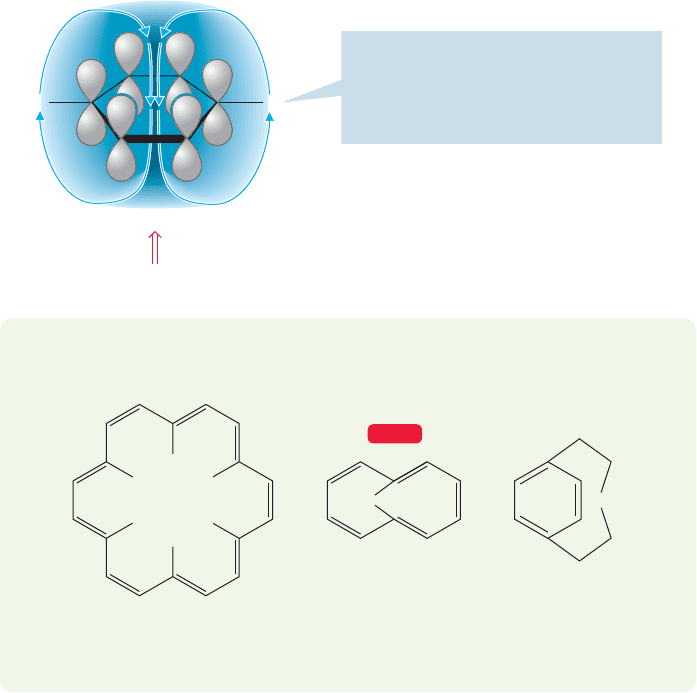
Aromaticity. Hydrogens on aromatic rings are found downfield from most

hydrogens attached to double bonds. In fact, so-called aromatic hydrogens can be

quite reliably diagnosed by the existence of signals in the range δ 6.5–8.0 ppm.The

reason for the downfield chemical shift is similar to that for hydrogens attached to

double bonds. The external magnetic field induces a circulation of electrons in the

ring (a “ring current”) that creates its own magnetic field B

opposing B

in the cen-

ter of the ring. At the edge of the ring where the hydrogens are, the induced mag-

netic field augments B

.Therefore, such hydrogens require a weaker applied magnetic

field to bring them into resonance (Figs. 15.31 and 15.33).

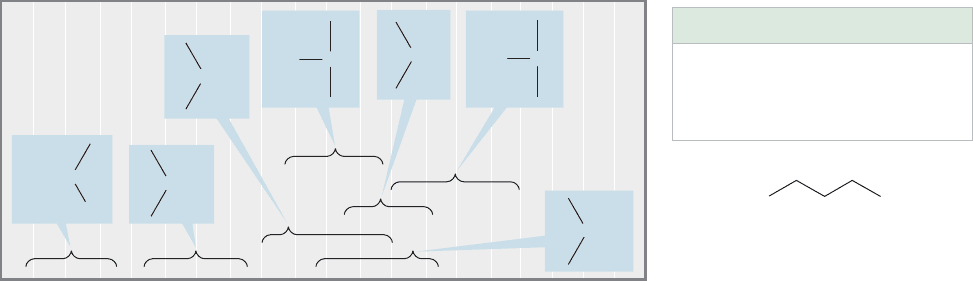
PROBLEM 15.15 Explain the unusual position (far upfield, above TMS) of the

hydrogens indicated in the following molecules:

At this point the induced magnetic field,

augments the applied field B

; the

hydrogen will “feel” a net magnetic field,

net

= B

+ B

, and require a reduced

applied field

come into resonance

FIGURE 15.33 The field induced (B

)

by the ring current of an aromatic

ring in an applied magnetic field (B

Hydrogens Attached to Oxygen or Nitrogen. Hydrogens attached to a carbon

bearing the electronegative oxygen or nitrogen atom of an alcohol or a primary or

secondary amine absorb, as we might expect,in the same region as the related hydro-

gens in ethers and tertiary amines (Fig. 15.28). But what about the OH and NH

hydrogens themselves? Here we do not see what a simple analysis would lead us to

expect. First of all, the chemical shifts of OH and NH vary greatly from sample to

sample.The problem is that these molecules are extensively hydrogen bonded. The

extent of hydrogen bonding depends on the concentration of the alcohol or amine,

the nature of the solvent, the pH of the solution, and the temperature. The chemi-

cal shift depends strongly on the chemical environment and thus on the extent of

hydrogen bonding.As a result,it is very difficult to predict where a hydrogen attached

to oxygen or nitrogen will appear. Generally, the less hydrogen bonding, the further

upfield the resonance appears. In the gas phase, where hydrogen bonding does not

occur, the chemical shifts of these hydrogens are about 1 ppm.

15.6 NMR Measurements 727

15.6c Spin–Spin Coupling: The Coupling Constant, J The utility of

NMR spectroscopy goes far beyond that of a simple hydrogen-detecting machine.

We can determine the number of different kinds of hydrogen in a molecule, and

gain a general idea of what chemical environments those hydrogens might occupy.

But there is much more information available.

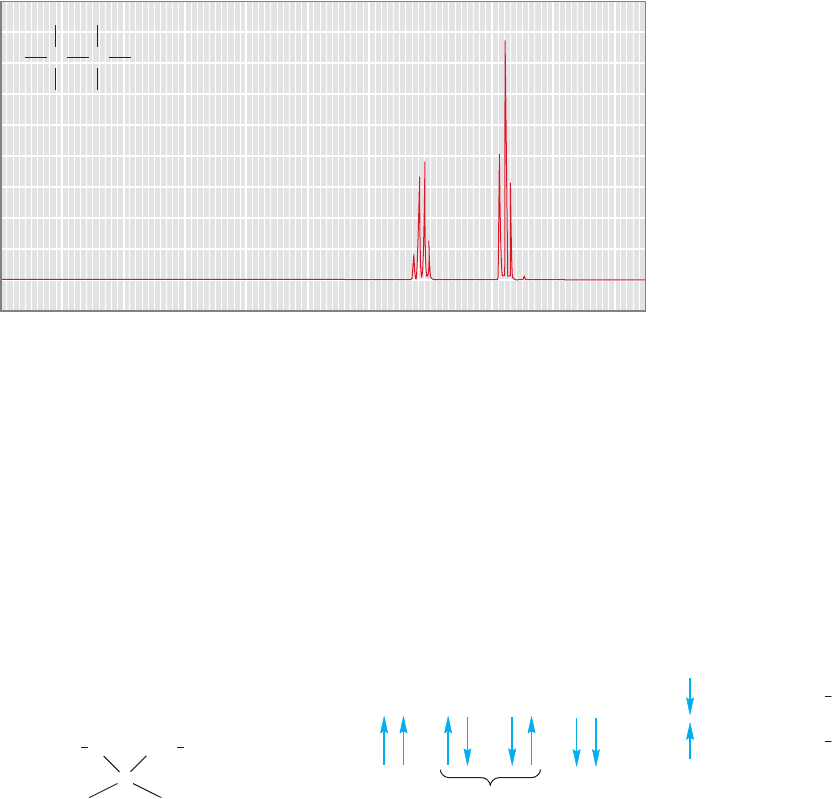
Most NMR spectra are not as simple as those of Figure 15.22 or Problem 15.10.

The signals in typical NMR spectra are not all single peaks, but are often multiplets

containing much fine structure. Ethyl iodide makes a nice example. Our initial expec-

tation might be that the spectrum would contain only two signals, one for the three

equivalent hydrogens of the methyl group and another for the two hydrogens of the

methylene group. A look at Table 15.4 would allow us to estimate the general posi-

tion for each peak. What we see, however, is somewhat different (Fig. 15.34). There

are signals at the positions we estimated, but each signal is composed of several lines.

They are not singlets as were most of the signals of the molecules in Problem 15.10.

The signal for the methyl hydrogens shows three lines (a triplet) in a 1:2:1 ratio cen-

tered at δ 1.85 ppm, and the methylene appears as four lines (a quartet) in the ratio

1:3:3:1, centered at δ 3.2 ppm.The spacings between the lines are all the same.

10 9 8 7 6 5 4 3 2

(ppm)

Chemical shift (δ)

FIGURE 15.34 The

H NMR

spectrum of ethyl iodide.The methyl

signal is a triplet and the methylene

signal is a quartet.

Our job is first to see how these multiple signals arise, and then to see how we

can use that information.

The (n ⴙ 1) Rule. The net magnetic field experienced by a hydrogen will be sig-

nificantly modified by adjacent (vicinal) hydrogens. Let’s start by examining the

triplet for the methyl hydrogens in Figure 15.34. To do this, we look first at the

neighboring methylene hydrogens.Each of the two equivalent methylene hydrogens

has a spin of either 

or 

.Therefore, there are four different combinations of

these spins, (



), (



), (



), and (



) (Fig. 15.35). The

methyl hydrogens will experience an applied magnetic field (B

) modified by each

Equivalent

Means spin = –

Means spin

= +

To explain the three-line signal for the

methyl hydrogens of ethyl iodide, look

first at the neighboring methylene hydrogens

The possible combinations for the

methylene hydrogens are

–

FIGURE 15.35 For two hydrogens there are four possible combinations of the nuclear spins.Two of

these combinations are equivalent.

728 CHAPTER 15 Analytical Chemistry: Spectroscopy

of the different spin combinations of the neighboring methylene hydrogens. So we

now expect to see four lines,one for each possible spin combination. But two of these

combinations,(



) and (



),are equivalent and will give rise to the same

net magnetic field, which is the reason we see only a three-line signal in approxi-

mately a 1:2:1 ratio for the methyl hydrogens (Fig. 15.36). The methyl hydrogens

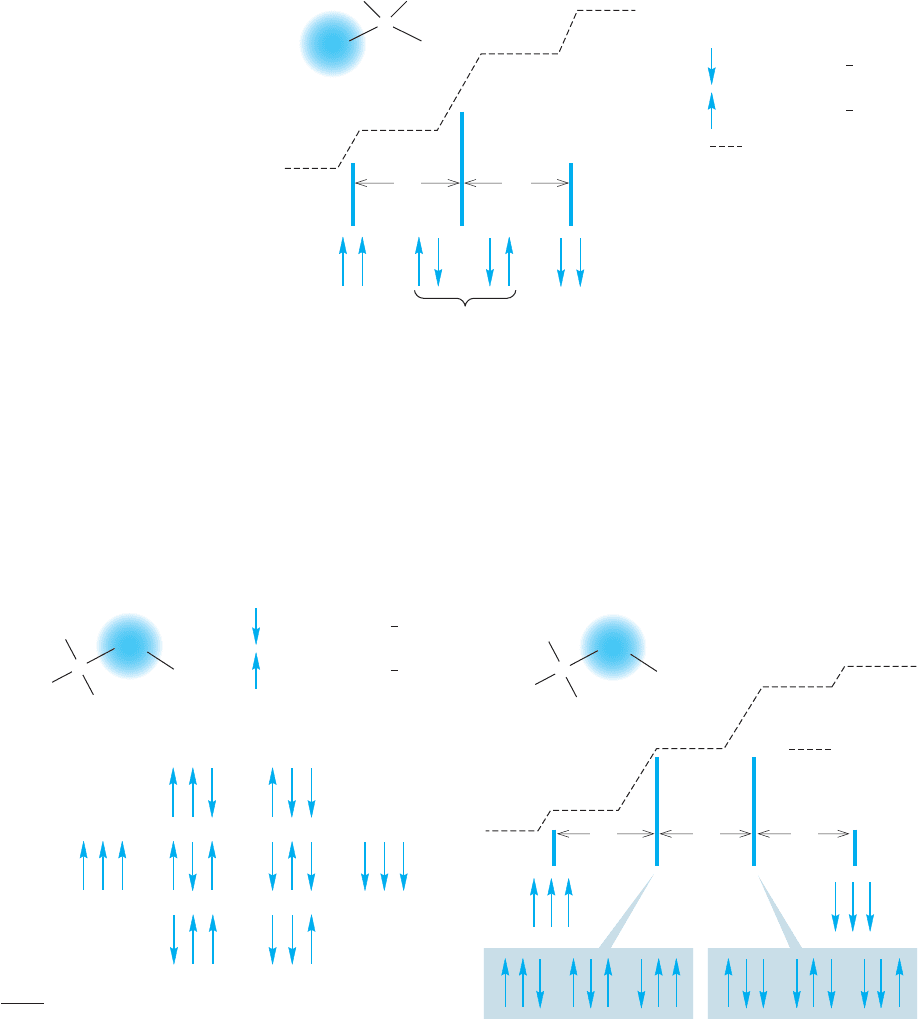
are said to be coupled to the adjacent methylene hydrogens. The distance between

any two of the lines, as mentioned earlier, is the coupling constant ( J ), and is

measured in hertz. In ethyl iodide the methyl signal is split by 7.6 Hz (Fig. 15.36).

Now let’s rationalize the four-line signal for the methylene hydrogens of ethyl iodide.

There are eight possible combinations of the nuclear spins of the three equivalent hydro-

gens that are vicinal to the methylene group (Fig. 15.37). Note that there are now two

sets of three equivalent spin combinations (two up and one down or one up and two

down).So,the methylene hydrogens feel an applied magnetic field modified by the four

different spin combinations of the adjacent methyl hydrogens. Accordingly, the spec-

trum consists of four lines in a 1:3:3:1 ratio, a quartet. The methylene hydrogens are

coupled to the methyl hydrogens with the same coupling constant, J  7.6 Hz,

by which the methyl hydrogens are coupled to the methylene hydrogens (Fig. 15.38).

7.6 Hz

Equivalent

Means spin = –

Means spin

= +

Integral

FIGURE 15.36 The methyl group

adjacent to the two methylene

hydrogens will be split into three

lines in the ratio 1:2:1.The splitting

between the lines is called the

coupling constant, J.

All three

Two up,

one down

One up,

two down

All three

down

Spins

Means spin = –

Means spin

= +

FIGURE 15.37 For the three methyl hydrogens in ethyl

iodide there are eight possible spin combinations, but

only four different energy combinations.

7.6 Hz

Integral

FIGURE 15.38 The signal for the methylene group of

ethyl iodide will be split into four lines in the ratio

1:3:3:1.