Jones M., Fleming S.A. Organic Chemistry

Подождите немного. Документ загружается.

15.6 NMR Measurements 739

15.6e Decoupled Spectra When we discussed the NMR spectra of alcohols

and amines, we encountered the phenomenon of chemical exchange of the OH and

NH hydrogens (Fig. 15.46). Rapid exchange of these hydrogens resulted in an aver-

aging of the coupling to adjacent hydrogens. Exchange effectively decoupled the

OH and NH hydrogens from hydrogens at adjacent positions. This same trick can

be accomplished electronically, and it can be very useful, or even essential in the

interpretation of NMR spectra.

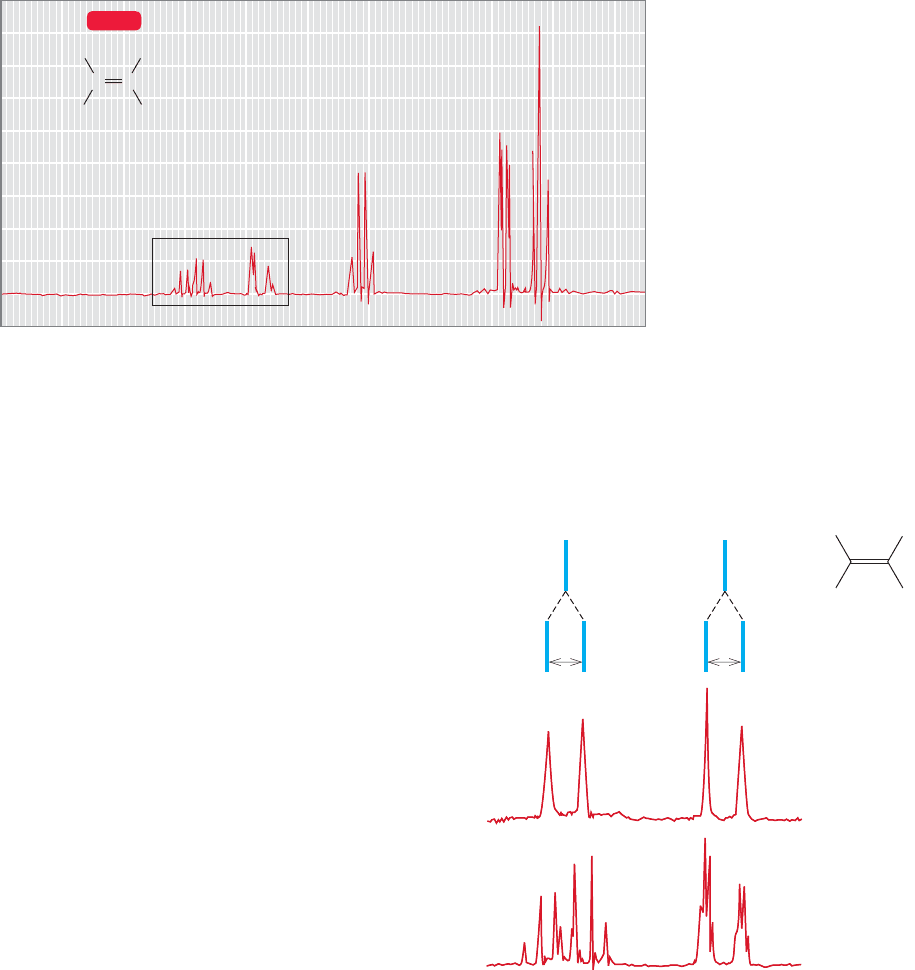
Suppose we are set the task of determining the stereochemistry of ethyl crotonate

from its

H NMR spectrum (Fig. 15.54). We might hope to make this distinction by

109876543210

(ppm)Chemical shift (δ)

Ethyl crotonate

COOC

WEB 3D

FIGURE 15.54 The

H NMR

spectrum of ethyl crotonate.The

coupling between H

and H

obscured by the coupling to the

adjacent methyl groups.

measuring the coupling constant between the two vinyl hydrogens. If the compound

is trans, we would expect J

to be 12–18 Hz; if it is cis, J

would be smaller, 6–12 Hz

(Fig. 15.43). However, the rather complex spectrum makes the determination of J

difficult.The problem is that both vinylic hydrogens are coupled to the methyl group,

and this coupling leads to the complex signals we see. If we

could somehow get rid of the coupling to the methyl group,

the spectrum would surely simplify, and it might become

possible to pick out the couplings between H

and H

. It is

possible to accomplish this simplification through electron-

ic decoupling. The spectrometer is modified to allow a sec-

ond application of radio-frequency waves during the NMR

experiment. While the spectrum is being measured, a radio

wave whose frequency matches the resonance frequency of

the methyl hydrogens is applied.The result is to induce rapid

transitions between the two possible spin states for each

methyl hydrogen. As in chemical exchange of ethyl alcohol,

the spin of the methyl hydrogens is averaged to zero and so

there is no observable coupling to H

or H

. Figure 15.55

shows a blow-up of the signals for the two vinyl hydrogens

with and without irradiation at the methyl group. It is now

easy to pick out the coupling between H

and H

and the

stereochemistry of the molecule can be determined with ease

from the observed J

of 17 Hz. The compound is trans.

There are many similar applications,and modern NMR

spectrometers are all equipped to do decoupling experi-

ments routinely.

Decoupled spectrum

with irradiation at

the methyl group

Normal, coupled

spectrum

J JJ

= 17 Hz

COOC

FIGURE 15.55 Irradiation at the resonance frequency of the

allylic methyl group averages the spins of the methyl hydrogens

and decouples them from H

and H

.The coupling constant J

between H

and H

is now easier to determine.

740 CHAPTER 15 Analytical Chemistry: Spectroscopy

15.7

C NMR Spectroscopy

Several other nuclei are of interest to the organic chemist, mainly

(deuterium),and

C,an isotope of carbon, which is present in 1.1% natural abundance.

Even though all organic compounds contain carbon, the natural abundance of

C is

low enough so that coupling to

C is not observed in hydrogen spectra. These other

nuclei can be used either in natural abundance or in enriched samples to provide their

own NMR spectra. Recall that the constant γ in Eq. 15.4 will be different for

N, or

C, and their NMR signals will not overlap with the hydrogen spectra.

For organic chemists, only

C is comparable in importance to

H. Like hydro-

gen,

C has a spin of

, and coupling between

C and

H will complicate

C spec-

tra.Normally,

C spectra are run using a broad-band decoupling so that all

coupling is removed. What about coupling between two

C atoms? Won’t this cou-

pling complicate the spectrum? The chance of finding a

C at any given position is

only 1.1% or 0.011.The chance of finding two

C atoms on adjacent positions is there-

fore 0.011  0.011  0.00012! At least for natural abundance spectra we can ignore

coupling. Accordingly,

C spectra are collections of sharp singlets. If the

broad-band decoupler is turned off, a spectrum can be obtained through a technique

called off-resonance decoupling, which allows the

C signals to be split according

to the n  1 rule, but only by the directly attached (not adjacent) hydrogens. Because

they have no attached hydrogens, quaternary carbons will still appear as singlets, but

methine carbons (one attached hydrogen) will be doublets, methylene carbons (two

attached hydrogens) triplets, and methyl carbons (three attached hydrogens) will appear

as quartets. Figure 15.56 summarizes this notion and shows the decoupled and off-

Carbonyl

carbon not

shown (165 ppm)

Broad-Band

Decoupled

Off-Resonance

Decoupled

Ethyl maleate

Broad-Band

Decoupled

Off-Resonance

Decoupled

This carbon is coupled

to three hydrogens and

will appear as a quartet

Singlet

This carbon is coupled

to two hydrogens and

will appear as a triplet

Singlet

This carbon is coupled

to one hydrogen and

will appear as a doublet

Singlet

This carbon is coupled

to no hydrogens and

will appear as a singlet

Singlet

OCH

Off-resonance decoupled spectrum

Chemical shift (δ)

61.45 14.15130.9 0

(ppm)

CH CH

Decoupled spectrum

WEB 3D

FIGURE 15.56 Decoupled and off-resonance

decoupled

C NMR spectra of ethyl

maleate.The carbonyl carbon is not shown

in either spectrum. It appears as a singlet at

δ 165 ppm.

15.7

C NMR Spectroscopy 741

resonance decoupled spectra of ethyl

maleate.Notice that

C NMR spectra are

not integrated.Only heights of similar car-

bons (methyls, methylenes, or methines)

can be compared to determine the relative

number of carbons giving rise to a signal.

Several other techniques now allow

for the easy determination of the number

of hydrogens attached to a carbon. One

of the most convenient techniques goes

by the acronym DEPT (distortionless

enhancement with polarization trans-

fer). In this technique, several separate

NMR spectra are determined for a mol-

ecule under conditions that allow for the

appearance of only methine (CH), meth-

ylene (CH

), or methyl (CH

) carbons.

Quaternary carbons can be determined

by difference: Any signal in the full spec-

trum that does not appear in the separate

spectra for CH, CH

, and CH

carbons

must belong to a quaternary carbon.

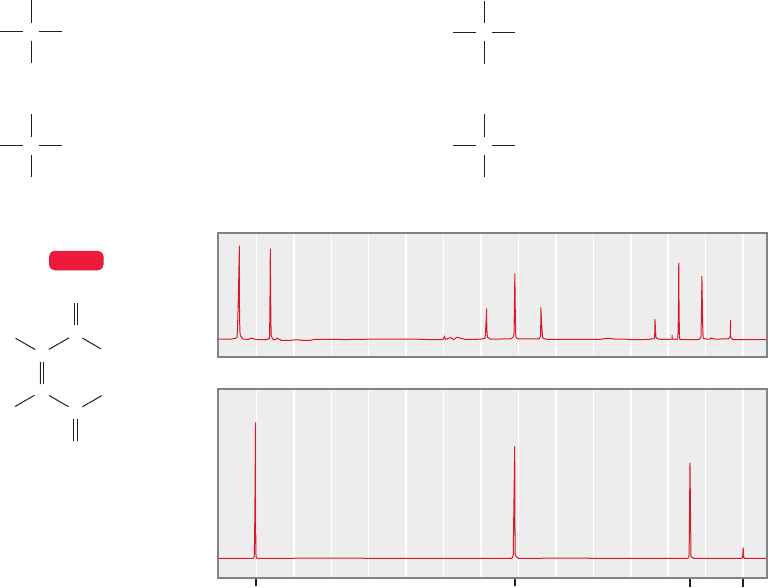
Figure 15.57 shows the DEPT technique applied by Kathryn Williams and Roy

W. King of the University of Florida to ethyl benzoate. The full

C spectrum is

shown on the bottom line,(e).The line (d) shows the signals for all carbons attached

to any number of hydrogens, note the absence of the signals for the quaternary

carbons at 130 and 166 ppm.The spectra on lines (c), (b), and (a) show the methine,

methylene, and methyl carbons, respectively.

Table 15.5 gives a series of chemical shift correlations for

C NMR. Notice the

greatly expanded range of chemical shifts extending over 200 ppm, as opposed to

the mere 10 ppm for

H (Table 15.4). The factors that give rise to chemical shifts

C NMR are the same as in

H NMR (electronegativity, hybridization,aromatic-

ity, and delocalization). Dispersion is much greater for

C NMR than for

H NMR.

(a) CH

(b) CH

(e) Unedited

(d) All CH

200 180 160 140 120 100 80 60 40 20

(ppm)

FIGURE 15.57 The DEPT technique applied to ethyl benzoate.

TABLE 15.5 Some

C Chemical Shifts

Type of Carbon Chemical Shift (␦)

Alkanes Alcohols, ethers

Methyl 0–30 50–90

Methylene 15–55 Amines

Methine 25–55 40–60

Quaternary 30–40 Halogens

Alkenes 70–80

80–145 25–50

Alkynes 10–40

70–90 20–10

Aromatics 110–170 Carbonyls,

Benzene 128.7 190–220

150–180

The chemical shift δ is in parts per million (ppm) from TMS.

RXC

O (X = O or N)

ClC

Once again, the question of memorization arises. Use Table 15.5 to work problems,

and you will automatically memorize the information you really need (if you do

enough problems!).

742 CHAPTER 15 Analytical Chemistry: Spectroscopy

15.8 Problem Solving: How to Use

Spectroscopy to Determine Structure

The task set here is an almost impossible one—to show in a practical way how to

use the various kinds of spectral data to come up with a structure. Every compound

is different,of course, and so there can be no absolutely general method.Even worse,

there are many different approaches; what works for you may not be the optimal

way for others. Yet, there are some general techniques that are useful, and we’ll try

to set them out here.Remember, though, as the old lady in New York answered,when

asked for directions on how to get to Carnegie Hall, “practice, practice, practice.”

For you, that ancient joke means, “do lots and lots of problems.” Nowhere else is

that advice so essential.

First of all, when confronted by a set of spectral charts or data derived from

them, try to determine the molecular formula. Sometimes it will be given, some-

times you can work it out. Other times, it may be obvious or at least likely from

the chemical reactions involved. Sometimes you may have only a molecular weight,

from the molecular ion of a MS for example. Either way, having a formula or

molecular weight lets you determine the degrees of unsaturation (p. 131) and see

what’s left once you have determined part of the structure.

Next, use any available IR data, along with NMR chemical shift data, to get an

idea of what functional groups are present.The most useful data usually come from

the NMR spectrum.The convention for reporting signals is to list the chemical shift

followed by parenthetical listing of the coupling and the integration. So the NMR

spectrum of 1-bromobutane (Fig. 15.53) would be δ 0.9 (t, 3H), 1.5 (sextet, 2H),

1.8 (quintet, 2H), 3.4 (t, 2H). Coupling information is given by using s for singlet,

d for doublet, t for triplet, q for quartet, dd for doublet of doublets, and so on. If

the coupling is indecipherable, then we use m for multiplet (or mess, if you want).

There are many items in the Additional Problems section that let you practice this

technique.

Surprisingly, symmetry is often all that is needed to solve a structural problem—

a simple counting of signals may be sufficient to make a choice between several

alternatives, so you should always look hard at symmetry before starting on any

detailed analysis.

WORKED PROBLEM 15.23 You have bottles containing three isomeric compounds,

A, B, and C, each of the formula C

. The only significant bands in the

IR spectra of all three compounds are at about 3050, 2950, and 1610 cm

1

. The

H NMR spectrum of A shows signals at δ 2.13 (s, 6H) and 6.88 (s, 1H); B shows

signals at δ 2.18 (s, 3H), 2.25 (s, 3H), and 6.89 (s, 1H); and C shows signals at

δ 2.11 (s, 3H), 2.19 (s, 3H), 2.22 (s, 6H), and 6.80 (s, 2H). The

C NMR spec-

trum of A shows lines at δ 131.02, 133.52, and 19.04 ppm. Compound B shows

signals at δ 133.76, 133.79, 126.88, 20.65, and 15.78 ppm. Compound C shows

signals at δ 136.15, 134.43, 131.69, 128.29, 20.74, 20.20, and 14.86 ppm. What

are the structures?

(continued)

15.8 Problem Solving: How to Use Spectroscopy to Determine Structure 743

ANSWER First of all, these compounds seem to be aromatic hydrocarbons. The

formula C

establishes that there are four degrees of unsaturation (p. 131),

and the IR spectra show both aromatic and aliphatic CH stretches, as well as a

band at 1610 cm

1

appropriate for an aromatic double-bond stretch. An aromatic

ring has three double bonds and a ring, which adds up to four degrees of unsatu-

ration. If six of the available carbons are tied up in an aromatic ring, the other

four must be attached in some way. A look at the

H NMR spectra shows only

singlets, and so the four remaining carbons are certainly methyl groups. The

chemical shift for each of the methyl groups is about δ 2.2, which is consistent

with a methyl group on an aromatic ring. Thus, putting the data together leads

to the idea that A, B, and C are the three possible tetramethylbenzenes. But

which is which?

To answer this question, there is no need to do anything more elaborate than

look at the number of signals.There is more than one way to do this, but let’s use

the methyl signals in the

H NMR spectrum. Compound A has only one methyl

signal, so all four methyl groups must be identical. This compound must be the

molecule on the left. Compound B has two methyl signals, and must be the struc-

ture in the middle. Of course, we now know that the remaining isomer must be

C, but it is gratifying that it has the appropriate three methyl signals. There was

no need to consider many details, only to use symmetry and count.

PROBLEM 15.24 Could we have used the aromatic CH signals in Problem 15.23

to determine the answer?

PROBLEM 15.25 Could we have used the

C NMR spectra in Problem 15.23 to

determine the answer?

PROBLEM SOLVING

In almost all spectroscopy problems in which NMR is used to distinguish

between various possible structures, the very first thing to do is count carbons

and/or hydrogens. Many otherwise quite tough problems can be shortcut, and

made much easier, by determining how many signals there will be. Problem

15.23 is a good example. Moreover, problem writers aren’t always aware that

simple counting can solve otherwise difficult problems. By counting, you may be

able to solve easily a problem that was meant to be very hard, and to require

specific detailed knowledge of spectroscopy. It happens all the time.

Chemical shift data are often decisive. After considering symmetry, that is what

we usually look at next. Table 15.4 will let you make many structural decisions.

WORKED PROBLEM 15.26 You have four bottles, each containing one of the four

compounds shown below, E, F,G, and H.From the spectral data given,determine

which bottle holds which compound.

OCH

All four compounds have signals for 4H in the aromatic region of the

H NMR

spectrum at δ 7–8 ppm.

Bottle 1 IR: 1720 cm

11

H NMR: δ 1.38 (t, 3H), 2.40 (s, 3H), 4.36 (q, 2H)

Bottle 2 IR: 1688 cm

11

H NMR: δ 1.12 (t, 3H), 2.81 (q, 2H), 3.76 (s, 3H)

Bottle 3 IR: 1725 cm

11

H NMR: δ 1.21 (t, 3H), 2.65 (q, 2H), 3.85 (s, 3H)

Bottle 4 IR: 1680 cm

11

H NMR: δ 1.40 (t, 3H), 2.50 (s, 3H), 4.07 (q, 2H)

ANSWER First, use Table 15.3 to determine that the two esters are in bottles 1 and

3 (IR: conjugated stretch at about 1720 cm

1

) and the two ketones are in

bottles 2 and 4 (IR: conjugated stretch much lower, at about 1680 cm

1

Now the chemical shift data allow a quick determination of the rest of the

problem. Again, there are several ways to do this last part, but the easiest is to

look at the chemical shift of the singlet methyl group (you could also use the

methylene quartet). Every signal has three pieces of data: integral,chemical shift,

and coupling. If we look at the chemical shift (δ 2.40) of the methyl (3H) sin-

glet in bottle 1, we see that it cannot be a methyl group attached to an oxygen.

Methyl groups on oxygen are at δ 3.2 or even further downfield. A methyl group

on an aromatic ring should be around δ 2.2 ppm. If the compound in bottle

1 must be an ester based on IR, then it must contain compound E. The ester

in bottle 3 has a 3H singlet at δ 3.85 ppm and is consistent with compound G.

A similar analysis of the ketones leads us to assign the 3H singlet at δ 2.50 ppm

in bottle 4 to the methyl ketone of compound H, and the 3H singlet at

δ 3.76 ppm in bottle 2 must be assigned to the methoxy group on the aromatic

ring in compound F.

744 CHAPTER 15 Analytical Chemistry: Spectroscopy

Sometimes the coupling constant J is the key to solving the puzzle, and often it

is the magnitude of J that is the key. The molecules in Problem 15.19 are a perfect

example of this use of J. More often, it is the splitting pattern that solves the prob-

lem. An examination of J reveals who is adjacent to whom in the hydrogen world,

and thus provides deep insight into structure.Here’s another problem, this time one

that requires you to think about J.

15.8 Problem Solving: How to Use Spectroscopy to Determine Structure 745

WORKED PROBLEM 15.27 Again you have bottles 1 and 2, this time containing I

and J. Explain how you would use

H NMR spectroscopy to tell which molecule

is in which bottle.

Now we pass on to some “bells and whistles” of NMR.

MAITOTOXIN

These days sophisticated NMR techniques seem capable of

determining any structure. This box is almost pure “gee-whiz.”

We are trying to dazzle you with the complexity of the molec-

ular structures that can be solved by the application of spec-

troscopy (and a lot of hard work). The example is maitotoxin.

Maitotoxin, a molecule for which one of your authors

maintains a certain affection, is extraordinarily lethal (for half

the mice treated the lethal dose is only 50 ng/kg) and is one

of the largest natural products known. In 1993, a group of

Japanese chemists reported a variety of complex NMR studies

that established the general structure, and in 1996, chemists at

Harvard used much spectroscopy, along with organic synthe-

sis, to establish the complete relative stereochemistry. That

same year the absolute stereochemistry was determined in

Japan by K.Tachibana (b. 1949) and his research group

at the University of Tokyo. How many stereogenic carbons are

there in maitotoxin? How many possible stereoisomers are

there? To solve this structure is a remarkable accomplishment.

Why show this molecule? No one is ever going to ask you

to reproduce the structure, we hope, and there are not likely to

be any immediate practical applications. We think that the

answer is simply that the sheer difficulty of the enterprise is

overwhelming. We humans can do some quite amazing things.

There are times when that gee-whiz factor must be confronted

directly, when we are allowed to sit back and marvel at some

accomplishment, and this is one of those moments.

OSO

NaO

ANSWER In compound J, the hydrogen adjacent to the phenyl group and the

hydrogen adjacent to the chlorine will couple. Each will appear as a doublet, with a

small coupling constant of a few hertz (Hz). The hydrogen adjacent to the phenyl

ring and the hydrogen adjacent to the chlorine in compound I are too far from each

other to couple; they will appear as singlets because identical hydrogens do not cou-

ple. Be sure you see that there is no other easy way to make this determination.

746 CHAPTER 15 Analytical Chemistry: Spectroscopy

15.9 Special Topic: Dynamic NMR

We have already seen that rates of hydrogen exchange are important in NMR spec-

troscopy. Recall that fast exchange of hydroxyl and amine hydrogens generally results

in a decoupling of the OH and NH hydrogens (p.733). An adjacent hydrogen “feels”

only an averaged perturbation of the applied magnetic field if exchange is fast enough.

If exchange is slowed by careful removal of all acidic or basic catalysts, the coupling

can be detected. The rate of exchange is important to the spectrum. If it is fast, the

NMR experiment detects an averaged spectrum; if it is slow, it sees a static picture.

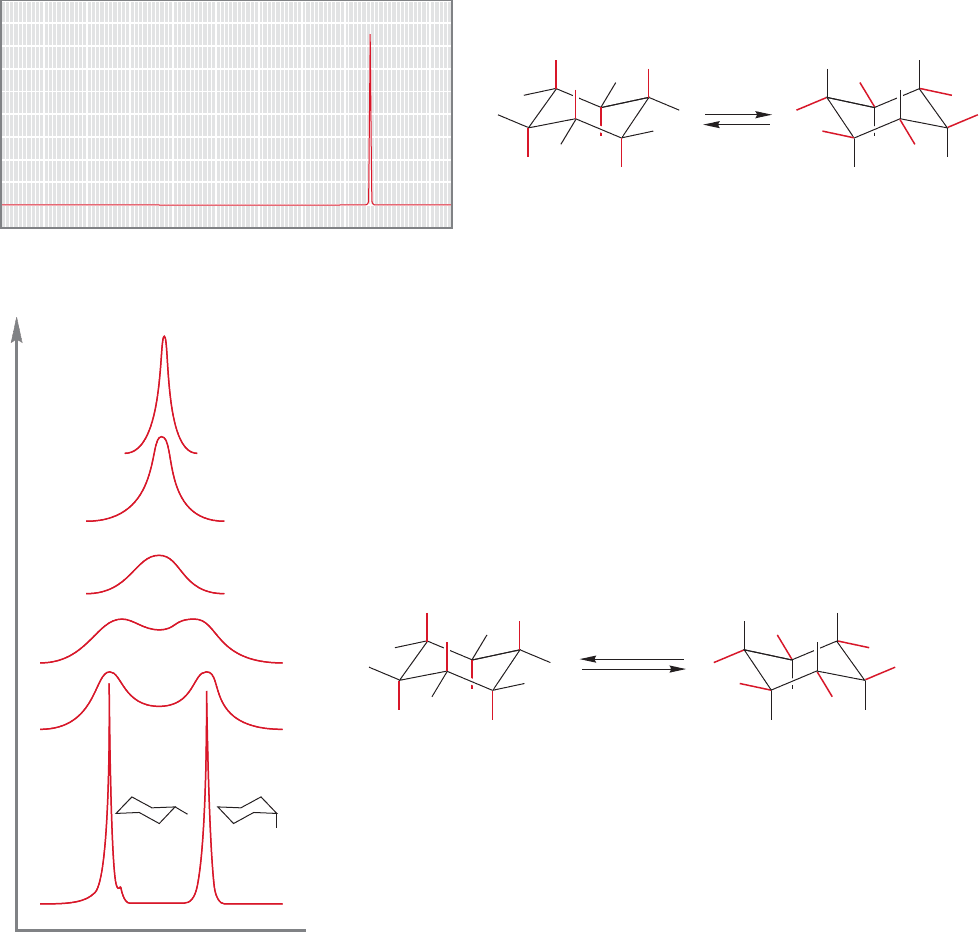
The classic example of this phenomenon involves the spectrum of cyclohexane.

As you know, there are two kinds of hydrogen in cyclohexane, axial and equatorial,

and these are interconverted by a ring flip, with an activation energy of about

11 kcal/mol (p. 198). Despite the existence of two kinds of hydrogen, the room-

temperature spectrum of cyclohexane shows only a single line at δ 1.4 ppm (Fig. 15.58).

ring

flip

109876543210

(ppm)Chemical shift (δ)

FIGURE 15.58 The

H NMR spectrum of cyclohexane at 25 °C.

ring flip

(ppm)

slow at

–89 ⬚C

–60 ⬚C

25 ⬚C

Each spectrum at higher temperature

–89 ⬚C

Equatorial

Axial

FIGURE 15.59 At low temperature, ring flipping is slowed and

the axial and equatorial hydrogens of cyclohexane can be

resolved in the NMR spectrum. As the temperature is raised, the

89 °C spectrum approaches the 25 °C spectrum.

This spectrum appears simple because the rate of interconversion of axial and equato-

rial hydrogens is so fast, with respect to the time necessary for the NMR measurement,

that the spectrum appears as an average. Suppose we decrease the energy available to

the system by lowering the temperature.If we can decrease the rate of the ring flip suf-

ficiently, the spectrometer will no longer detect an average of the two possible positions

but will be able to see both axial and equatorial hydrogens. Figure 15.59 shows the

NMR spectrum of undecadeuteriocyclohexane (cyclohexane-d

) at 89 °C.Two equal

signals appear, centered on the position of the room temperature, averaged signal.

15.9 Special Topic: Dynamic NMR 747

In practice, for a signal to be detectable for a given species, it must have a life-

time of about 1 s. As the temperature is raised to room temperature, the lifetime of

individual cyclohexanes decreases as the rate of ring flipping increases, and an aver-

aged spectrum appears.

Now, what happens at an intermediate temperature? Figure 15.59 shows you. A

common-sense answer would be correct here. If two signals are found at 89 °C,

and a single signal at 25 °C, at intermediate temperatures the two kinds of signal

must approach each other.The two sharp peaks of the 89 °C spectrum will slow-

ly merge into the single peak of the 25 °C spectrum. In fact, it is possible to derive

kinetic information from the temperature dependance of NMR spectra, and this is

still another use of NMR spectroscopy.

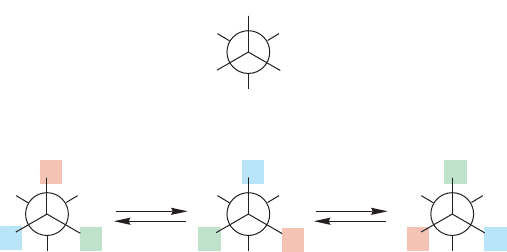
More molecules than you might at first expect give this kind of averaged spec-

trum. It takes a detailed look at structure to see why. Consider ethyl alcohol. If we

ignore the OH signal, which we know to be dependent on concentration,pH, sol-

vent, and temperature, we expect to see only one signal for the three equivalent

methyl hydrogens and another for the two equivalent methylene hydrogens. But

wait—look at the Newman projection in Figure 15.60, which shows the most sta-

ble staggered conformation of ethyl alcohol.This perspective shows that there are

three kinds of hydrogen (H

, and H

), not two. The three methyl hydrogens

are not all the same.The two that are gauche to the alcohol are in a different envi-

ronment from the hydrogen that is anti to the alcohol. Yet, we do not see sepa-

rate signals for these hydrogens. By now you should be able to see the answer to

this conundrum. As shown in Figure 15.60, rotation about the carbon–carbon bond

of ethyl alcohol interconverts the three methyl hydrogens, rendering them equiv-

alent. Moreover, we know that the low barrier for rotation, about 3 kcal/mol,

ensures a rapid rate for this simple process.In Figure 15.60, the hydrogens are indi-

vidualized with colored squares. Note how each methyl hydrogen occupies one of

the three possible positions as rotation occurs.The NMR spectrometer detects only

the averaged signal.

120⬚ 120⬚

FIGURE 15.60 In static ethyl alcohol,

there are three kinds of hydrogen

attached to carbon. However, rapid

rotation around the carbon–carbon

bond interconverts the methyl

hydrogens and makes them

equivalent.The two methylene

hydrogens are enantiotopic.

What about the two methylene hydrogens, H

? The Newman projection of

Figure 15.60 shows that even in the absence of rapid rotation they are equivalent,

and therefore must always give rise to one signal.These hydrogens are enantiotopic.

As we saw earlier, the origin of the name lies in the mirror-image relationship of

the two to each other.

So, as long as rotation is fast, neither the individual methyl hydrogens nor the

individual methylene hydrogens of ethyl alcohol are distinguishable by NMR

spectroscopy.

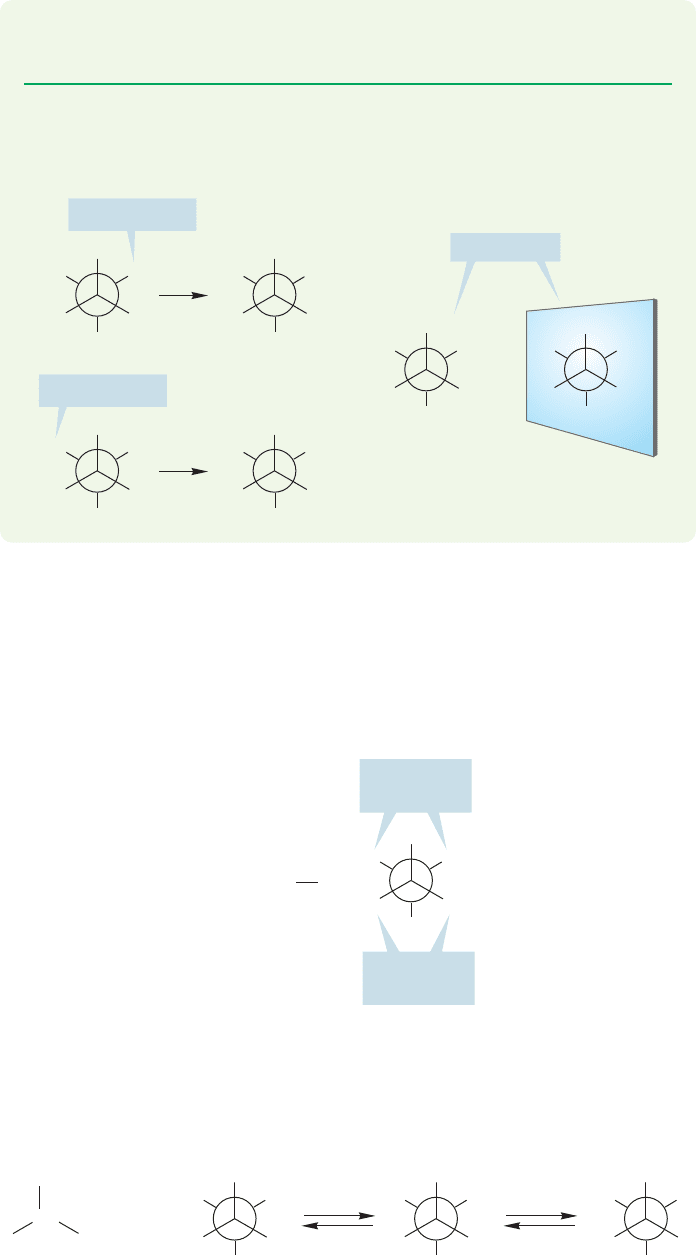
PROBLEM 15.28 In a solvent consisting of a single enantiomer, the two enantiotopic

hydrogens of ethyl alcohol (H

in Fig. 15.60) appear as separate signals. Explain.

WORKED PROBLEM 15.29 Use the device of replacing the methylene hydrogens

in Fig. 15.60) with an X group to show that they are enantiotopic (p. 721).

ANSWER

748 CHAPTER 15 Analytical Chemistry: Spectroscopy

Mirror

X H

Replace with X

Enantiomers

Now let’s change some things about ethyl alcohol. Let’s first convert it into

1-propanol by replacing one methyl hydrogen with a methyl group (Fig. 15.61).

There are now three sets of hydrogens: the methyl hydrogens and two different sets

of methylene hydrogens. Rapid rotation ensures that the three methyl hydrogens will

be equivalent, and each pair of methylene hydrogens consists of two magnetically

equivalent, enantiotopic hydrogens.

Enantiotopic

hydrogens

Newman projection

Enantiotopic

hydrogens

FIGURE 15.61 In propyl alcohol, the

methyl hydrogens are homotopic;

there are two pairs of enantiotopic

methylene hydrogens.

Next let’s replace a hydrogen of 1-propanol with a chlorine to make 2-chloro-

1-propanol. Look at the Newman projection of this molecule in Figure 15.62.

120⬚ 120⬚

Is H

equivalent to H

2-Chloro-1-propanol

12 3

FIGURE 15.62 In 2-chloro-

1-propanol, the two methylene

hydrogens, H

and H

, are neither

equivalent (homotopic) nor

enantiotopic.