Klein B. FEM: Grundlagen und Anwendungen der Finite-Element-Methode im Maschinen - und Fahrzeugbau
Подождите немного. Документ загружается.

378
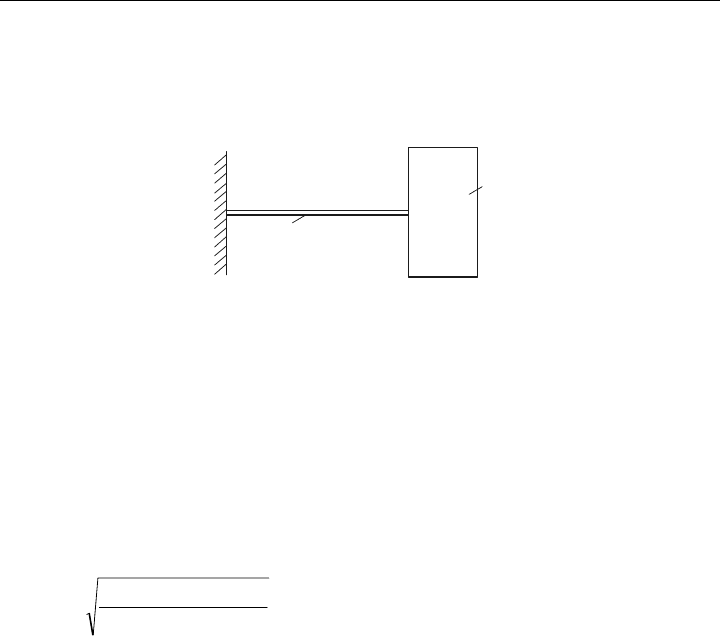
Übungsaufgabe 9.3
Ermitteln Sie bei dem skizzierten Torsionsschwinger die 1. Eigenfrequenz!
J
M
U
, G, J , L
p
Gehen Sie dabei schrittweise vor, indem Sie
die Bewegungsgleichung für die freie ungedämpfte Schwingung aufstellen,
die Randbedingungen einarbeiten,
das Gleichungssystem lösen.
Ergebnis
Mp
p
J3LJL
JG3
U
Z
379
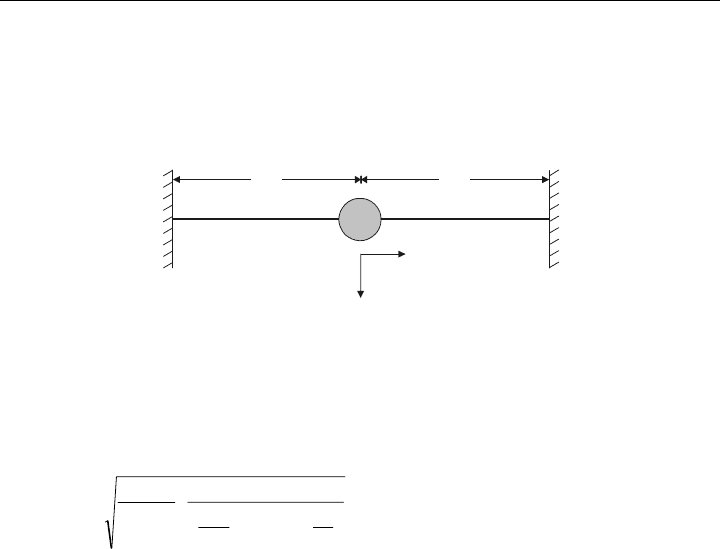
Übungsaufgabe 9.4
Gegeben sei das dargestellte schwingfähige System. Berechnen Sie für dieses System die
ersten Eigenfrequenzen!
M
L
L
z, w
x, u
Beachten Sie, dass sich hier die Symmetrie des Modells gut nutzen lässt.
Ergebnis
¸
¹
·
¨
©
§
U
Z
2
M
LA
420
156
1
L
JE12
3
1
380
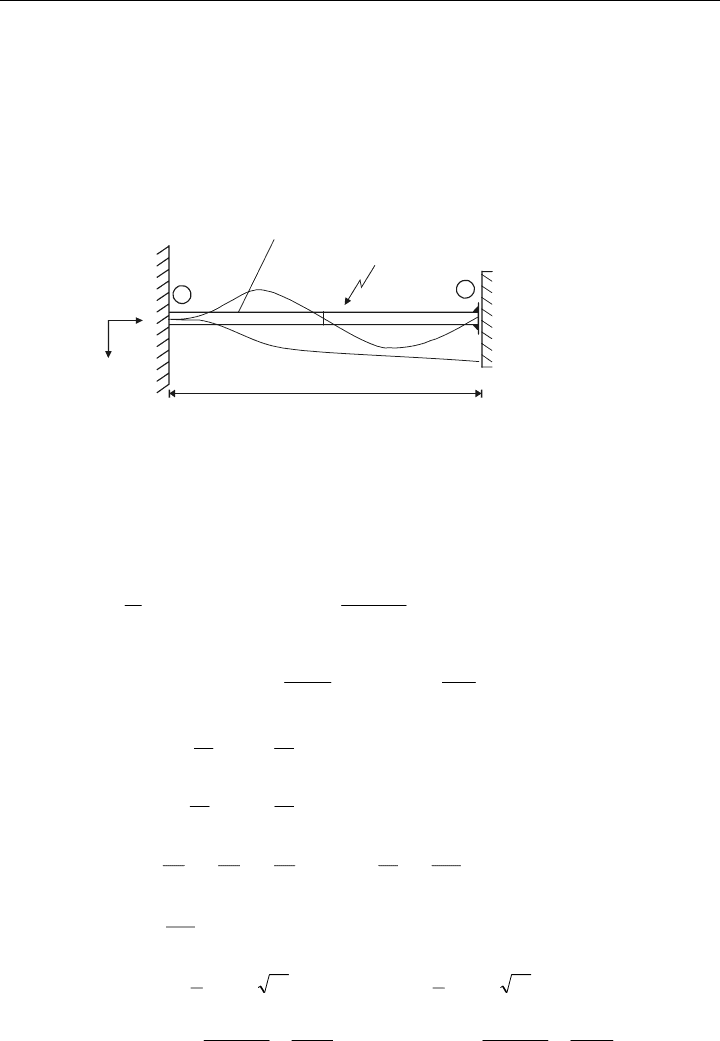
Übungsaufgabe 10.4
Der dargestellte Balken ist links fest eingespannt und rechts verschiebbar gelagert. Der Bal-
ken erfährt eine gleichmäßige Temperaturerhöhung 'T. Berechnen Sie nach der FE-
Methode in erster Näherung die ersten beiden „kritischen Temperaturerhöhungen“ 'T
krit
, bei
welcher der Balken mit seinen Eigenformen knickt!
x
z, w
E, A, J
2L
1
2
E = 1
J = 1
L = 1
A = 1
2
T
10
D
T
'
Beachten Sie, dass die erste Eigenform aus einem Stab-Modell und die zweite Eigenform
aus einem Balken-Element bestimmt werden kann.
Ergebnisse
1. Eigenform:
TE
A
F
'D ,
AE
F
T
krit
krit
D
'
2. Eigenform:
¸
¸
¹
·
¨
¨
©
§
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
22
3
y
N
L4L3
L336
L30
F
L4L6
L612
L
JE
detdet KK
0
F
15
2
4F
10
1
6
F
10
1
6F
15
18
12
det
»
»
»
»
¼
º
«
«
«
«
¬
ª
18,3231213
3
4
F,49,231213
3
4
F
080F
3
104
F
0F
100
1
F
10
12
36F
75
12
F
5
24
F
15
24
48
1,krit1,krit
2
22
218.3
10
18,32
EA
F
T,249
10
49,2
EA
F
T
2
T
2,krit
2,krit
2
T
1,krit
1,krit
D
'
D
'

381
Übungsaufgabe 11.1
Stellen Sie für das gezeigte Kabelstück ein finites „Einelement-Modell“ auf, welches den
stationären Zusammenhang zwischen den Wärmeflüssen und der Temperatur wiedergibt!
d
x
L
Q
1
Q
2
T
1
T
2
x
,
T
A
1
2
Gehen Sie dabei schrittweise vor, indem Sie
die eindimensionale Fourier’sche Wärmeleitungsgleichung aufstellen,
den Zusammenhang zwischen der Wärmestromdichte und den Wärmeeinflüssen her-
stellen
und
einen linearen Ansatz benutzen.
Ergebnis
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
O
2
1
2
1
Q
Q
T
T
11
11
L
A
382
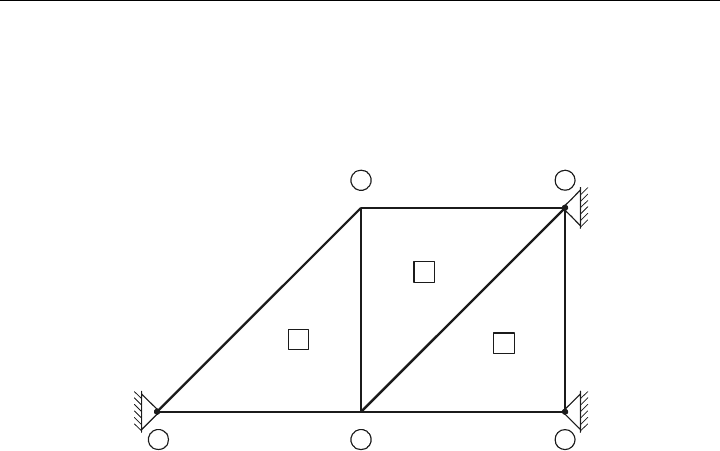
Übungsaufgabe 11.2
Ermitteln Sie für das aus Scheiben-Elementen bestehende FE-Modell die Temperaturen an
den Knotenpunkten!
1212
3
23
3
1
5
1 2
3
4
1
3
2
Gegeben:
KK
WW
12
110
12 1
011
ª
¬
«
«
«
º
¼
»
»
»
K
W
3
10 1
01 1
112
ª
¬
«
«
«
º
¼
»
»
»
Knotentemperaturen:
C0T
C0T
C100T
5
4
1
q
q
q
Gehen Sie dabei schrittweise vor, indem Sie
in Analogie zur Verschiebungsanalyse die Gesamtwärmeleitungsmatrix bestimmen,
die Gesamtwärmeleistungsbeziehungen erstellen,
das reduzierte System nach den unbekannten Temperaturen auflösen,
die Temperaturen an den Knoten d und e berechnen.
Ergebnisse
T
T
3
2
25
37,5

383
Mathematischer Anhang

Mathematischer Anhang
384
Zielsetzung des Anhanges soll es sein, die vorstehenden Darlegungen zur Mathematik und
Mechanik, insbesondere für den im Selbststudium lernenden FEM-Interessenten, noch etwas
vertiefter darzustellen bzw. über einige Lücken schnell hinwegzuhelfen.
A) Vektoren und Matrizen
Die Rechnung mit Vektoren und Matrizen hat in der ganzen MKS- und FEM-Theorie große
Bedeutung, weshalb hier einige Grundbeziehungen wiederholt werden sollen.
Zunächst existieren in der Vektorrechnung mehrere „Produkte“, die entsprechend richtig
ausgerechnet werden müssen:
Skalarprodukt zweier Vektoren
zzyyxx
bababa,cos
bababa , (A1)
Vektorprodukt zweier Vektoren
xyyxzxxzyzzy
baba,baba,babax
ba
(A2)
yxzyx
yxzyx
bbbbb
aaaaa
jikji
,
Spatprodukt (mehrfache Produkte)
zyx
zyx
zyx
ccc
bbb
aaa
,,x cbacba (A3)
bzw. das dreifache Vektorprodukt
acbbcacba
xx . (A4)
Die Matrizenrechnung wurde etwa 1850 von dem englischen Mathematiker Sylvester ent-
wickelt. Eine Matrix bezeichnet eine rechteckige Anordnung von Größen in m-Zeilen und n-
Spalten, z. B.
»
»
»
»
¼
º
«
«
«
«
¬
ª
mn3m2m1m
n2232221
n1131211
aaaa
aaaa
aaaa
"
##
"
"
A . (A5)
Dieser Matrix
A kann man direkt keinen Wert zuordnen, dagegen können die Elemente a
ij
Zahlen, Funktionen oder selbst wieder Matrizen sein.

Mathematischer Anhang
385
Von einer Quadratmatrix kann weiter eine
Determinante bildet werden. Dies ist eine
Rechenvorschrift, die auf einer Matrix anzuwenden ist, und zwar
nn2n1n
n22221
n11211
aaa
aaa
aaa
det
"
##
"
"
A . (A6)
Zum Beispiel lautet die Determinante einer 2-x-2-Matrix
12212211
2221
1211
aaaa
aa
aa
. (A7)
Verschwindet die Determinante einer Matrix (det
A = 0), so bezeichnet man die Matrix als
singulär.
Die
inverse Matrix
1
A einer nicht-singulären Quadratmatrix A ist definiert durch die Be-
ziehung
IAAAA
11
. (A8)
Mittels der Inversion lässt sich die in der gewöhnlichen Zahlenrechnung definierte Division
in die Matrixalgebra übertragen. Zur Demonstration der Inversion soll das folgende lineare
Gleichungssystem gegeben sein:
,yxaxaxaxa
,yxaxaxaxa
,yxaxaxaxa
nnnn33n22n11n
2nn2323222121
1nn1313212111
"
#
"
"
(A9)
welches symbolisch in Matrixform geschrieben werden kann:
yxA . (A10)
Hierbei sei angenommen, dass alle
a
ij
bekannt sind und auch der Vektor y gegeben sei. Die
Auflösung nach dem unbekannten
x erfolgt wieder aus einer linearen Gleichung heraus, und
zwar aus
,yayayayax
,yayayayax
,yayayayax
nnn33n22n11nn
nn23232221212
nn13132121111
"
#
"
"
(A11)
Mathematischer Anhang
386
welches ebenfalls symbolisch geschrieben werden kann als
yAx
1
. (A12)
Um eine derartige Inversion überschaubar darstellen zu können, soll von folgendem Glei-
chungssystem ausgegangen werden:
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
3
2
1
3
2
1
333231
232221
131211
y
y
y
x
x
x
aaa
aaa
aaa
. (A13)
Für die Bestimmung der unbekannten
x
i
wählen wir die so genannte Cramer‘sche Regel,
die zunächst zu folgender Lösung führt:
AA det
yaa
yaa
yaa
x,
det
aya
aya
aya
x,
aaa
aaa
aaa
aay
aay
aay
x
33231
22221
11211
3
33331
23221
13111
2
333231
232221
131211
33323
23222
13121
1
. (A14)
Im Prinzip sind die auftretenden Determinanten mit der
Sarrus’schen Regel (aber nur 3-x-3-
Matrix) bestimmbar. Hier soll aber kein Sonderfall, sondern die allgemeine Determinanten-
bestimmung nach dem Laughton-Prinzip
*)
dargestellt werden. Beliebige Determinanten
können somit entweder nach der Spalte oder nach der Zeile /RIE 96/ entwickelt werden. Die
Formeln dazu lauten:
j-te Spaltenentwicklung
¦
n
1i
ijij
ji
njnj
jn
j2j2
j2
j1j1
j1
,Adeta)1(Adeta)1(
Adeta)1(Adeta)1(Adet
"
i-te Zeilenentwicklung
¦
n
1j
ijij
ji
inin
ni
2i2i
2i
1i1i
1i
.Adeta)1(Adeta)1(
Adeta)1(Adeta)1(Adet
"
*)
Anmerkung: Charles Laughton (16. Jahrhundert), englischer Mathematiker,
verallgemeinerte die Cramer’sche Regel und das Sarrus-Prinzip.
Mathematischer Anhang
387
Zur Entwicklung der Determinanten nach den Spalten wollen wir hilfsweise noch die
Adjunten-Regel benutzen. Man erhält so
, (A15)
die Zählerdeterminanten entsprechend dem nachfolgenden Algorithmus entwickelt werden:
ya a
ya a
ya a
y
aa
aa
y
aa
aa
y
aa
aa
aya
aya
aya
y
aa
aa
y
aa
aa
y
aa
aa
aa y
aay
aay
y
aa
aa
y
aa
aa
y
aa
aa
11213
22223
33233
1
22 23
32 33
2
12 13
32 33
3
12 13
22 23
11 1 13
21 2 23
31 3 33
1
21 23
31 33
2
11 13
31 33
3
11 13
21 23
11 12 1
21 22 2
31 32 3
1
21 22
31 32
2
11 12
31 32
3
11 12
21 22
. (A16)
Die invertierte Matrix kann so angegeben werden als
2221
1211
3
3231
1211
2
3231
2221
1
2321
1311
3
3331
1311
2
3331
2321
1
2322
1312
3
3332
1312
2
3332
2322
1
1
aa
aa
y
aa
aa
y
aa
aa
y
aa
aa
y
aa
aa
y
aa
aa
y
aa
aa
y
aa
aa
y
aa
aa
y
det
1
A
A (A17)
mit
122133112332132231
322113312312332211
aaaaaaaaa
aaaaaaaaa
(A18)
In Kapitel 4 ist die Inversion einer 2-x-2-Matrix
»
¼
º
«
¬
ª
2221
1211
aa
aa
A (A19)
erforderlich. Wendet man hierauf das vorstehende Prinzip an, so führt dies zu
3231333231
2221232221
1211131211
aaaaa
aaaaa
aaaaa
det A
