Klein B. FEM: Grundlagen und Anwendungen der Finite-Element-Methode im Maschinen - und Fahrzeugbau
Подождите немного. Документ загружается.


5 Das Konzept der Finite-Element-Methode
58
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
¬
ª
s
c
s
c
s
c
s
c
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
¬
ª
¦
¦
¦
¦
4
1i
ii4i4
4
1i
ii3i3
4
1i
ii2i2
4
1i
ii1i1
y
K
2
2
1
1
K
d
o
L
gggg
d
o
L
gggg
d
o
L
gggg
d
o
L
gggg
JE
M
Q
M
Q
'''
'''
'''
'''
p . (5.49)
Offen ist aber jetzt noch, wie die Formfunktionen zu wählen sind. Im vorliegenden Fall
wollen wir diese so bestimmen, dass die Biegelinie mit ihren Randbedingungen erfüllt wird.
Demzufolge gehen wir von der speziellen DGL aus:
0xw
IV
.
*)
(5.50)
Die Durchbiegung w erhält man nun durch viermalige Integration über die Stufen
3
cw
ccc
,
xccw
32
cc
,
2
x
cxccw
2
321
c
,
6
x
c
2
x
cxccw
3
3
2
21o
. (5.51)
Werden hierin die Randbedingungen des Elements, d. h. an den Stellen x, L, die Knotenfrei-
heitsgrade eingesetzt, so kommt man zu den Integrationskonstanten
1o
wc0xw {
, (5.52)
11
c0xw \{
c
, (5.53)
2
3
3
2
211
w
6
L
c
2
L
cLwLxw {\ , (5.54)
2
2
321
2
L
cLcLxw \{\
c
. (5.55)
*)
Anmerkung: Normalerweise ist )x(qw
z
IV
; nachfolgend soll aber ein finites Element für Knotenlast-
einleitung hergeleitet werden.

5.3 Mathematische Formulierung
59
Die beiden unbekannten Konstanten
cc
23
, gewinnt man aus den letzten beiden Gleichungen
durch elementare Umformung ((5.54) + (5.55)
.
(-L/2) o
cc
33
, in (5.54) o c
2
)) zu
¸
¹
·
¨
©
§
\
\
2
L
2
L
ww
L
12
c
21
21
3
3
(5.56)
und
LL2w3w3
L
2
c
2121
2
2
\\ . (5.57)
Durch Einsetzen in Gl. (5.51) folgt letztendlich
,L
L
x
L
x
w
L
x2
L
x3
L
L
x
L
x2
L
x
w
L
x2
L
x3
1xw
2
3
3
2
2
2
3
3
2
2
1
3
3
2
2
1
3
3
2
2
\
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
\
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
(5.58)
d. h. eine Beziehung, wie die Durchbiegung an einer beliebigen Stelle x mit den festen Kno-
tengrößen
ww
112 2
,, ,\\ verknüpft ist. Nimmt man weiter Bezug zu Gl. (5.41), so wird
offensichtlich, dass die Formfunktionen vorstehend bestimmt sind als
,
¸
¸
¹
·
¨
¨
©
§
3
3
2
2
1
L
x2
L
x3
1g
,L
L
x
L
x2
L
x
g
3
3
2
2
2
¸
¸
¹
·
¨
¨
©
§
(5.59)
,
L
x2
L
x3
g
3
3
2
2
3
¸
¸
¹
·
¨
¨
©
§
.L
L
x
L
x
g
3
3
2
2
4
¸
¸
¹
·
¨
¨
©
§
Bezogen auf die normierte Koordinate
L
x
[
zeigt umseitig das Bild 5.7 den Verlauf dieser Formfunktionen (Hermite Polynome), die so-
wohl die Knotenverschiebungen als auch die Neigungen der Biegelinie wiedergeben können.

5 Das Konzept der Finite-Element-Methode
60
1 2
0,2
0,2
0,4
0,6
0,6
1,0
1,0
0,8
0,8
0
0,4
[
L
x
[
1
g
2
g
3
g
4
g
Bild 5.7: Ansatzfunktionen für das Balken-Element
Für die Bestimmung der hier interessierenden Massen- und Steifigkeitsmatrizen müssen jetzt
noch die zu Gl. (5.40) zugehörigen Ableitungen gebildet werden, und zwar
.
L
6
'''gL,
L
x6
L
2
gL,
L
x3
L
x2
g
,
L
12
'''g,
L
x12
L
6
g,
L
x6
L
x6
g
)62.5(,
L
6
'''g)61.5(L,
L
x6
L
4
g)60.5(L,
L
x3
L
x4
L
1
g
,
L
12
'''g,
L
x12
L
6
g,
L
x6
L
x6
g
2
4
32
4
3
2
2
4
3
3
32
3
3
2
2
3
2
2
32
2
3
2
2
2
3
1
32
1
3
2
2
1
¸
¸
¹
·
¨
¨
©
§
s
¸
¸
¹
·
¨
¨
©
§
c
s
c
¸
¸
¹
·
¨
¨
©
§
s
¸
¸
¹
·
¨
¨
©
§
c
s
c
Mit den somit vollständig vorhandenen Formfunktionen sollen jetzt gemäß Gl. (5.46) und
(5.47) exemplarisch einige Matrizenkoeffizienten berechnet werden:
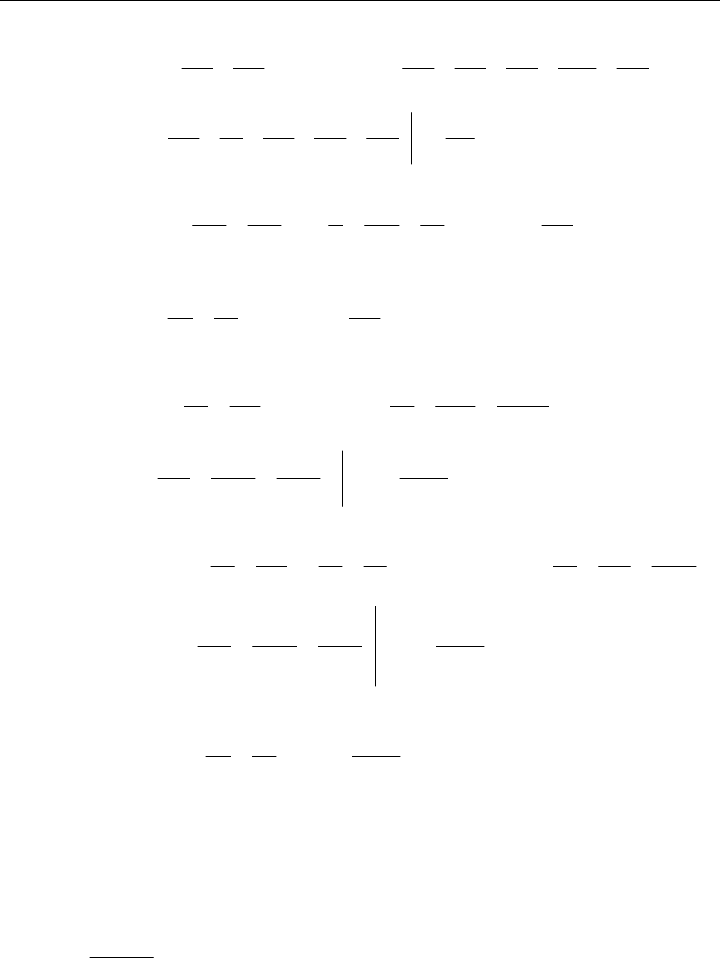
5.3 Mathematische Formulierung
61
,LA
420
156
o
L
L7
x4
L
x2
L5
x9
L
x
L
x2
xA
dx
L
x4
L
x12
L
x9
L
x4
L
x6
1Adx
L
x2
L
x3
1Am
6
7
5
6
4
5
3
4
2
3
L
o
6
6
5
5
4
4
3
3
2
2
2
L
o
3
3
2
2
11
U
»
»
¼
º
«
«
¬
ª
U
¸
¸
¹
·
¨
¨
©
§
U
¸
¸
¹
·
¨
¨
©
§
U
³³
,
2
3
3
2
2
L
o
3
3
2
2
12
LA
420
22
dxL
L
x
L
x2
L
x
L
x2
L
x3
1Am U
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
U
³
#
32
2
L
o
3
3
2
2
44
LA
420
4
dxL
L
x
L
x
Am U
¸
¸
¹
·
¨
¨
©
§
U
³
;
,
L
JE
12
o
L
L
x48
L
x72
L
x36
JE
dx
L
x144
L
x144
L
36
JEdx
L
x12
L
x6
JEk
3
y
2
6
3
5
2
4
y
L
o
6
2
54
y
L
o
2
32
y11
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¹
·
¨
©
§
³³
#
,
2
y
6
3
5
2
4
y
L
o
6
2
54
y
L
o
3232
y12
L
JE
6
o
L
L
x24
L
x42
L
x24
LJE
dx
L
x72
L
x84
L
24
LJEdx
L
x6
L
4
L
x12
L
6
LJEk
»
»
¼
º
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
³³
.
L
JE
4dx
L
x
L
x
LJEk
y
L
o
2
3
3
2
2
2
y44
¸
¸
¹
·
¨
¨
©
§
³
Würde man nun alle Kombinationen von Indizes bilden, so erhielte man jeweils vollständig
die Massenmatrix
»
»
»
»
¼
º
«
«
«
«
¬
ª
2
22
L4sym.
L22156
L3-L13-L4
L1354L22-156
420
LAȡ
m (5.63)
und
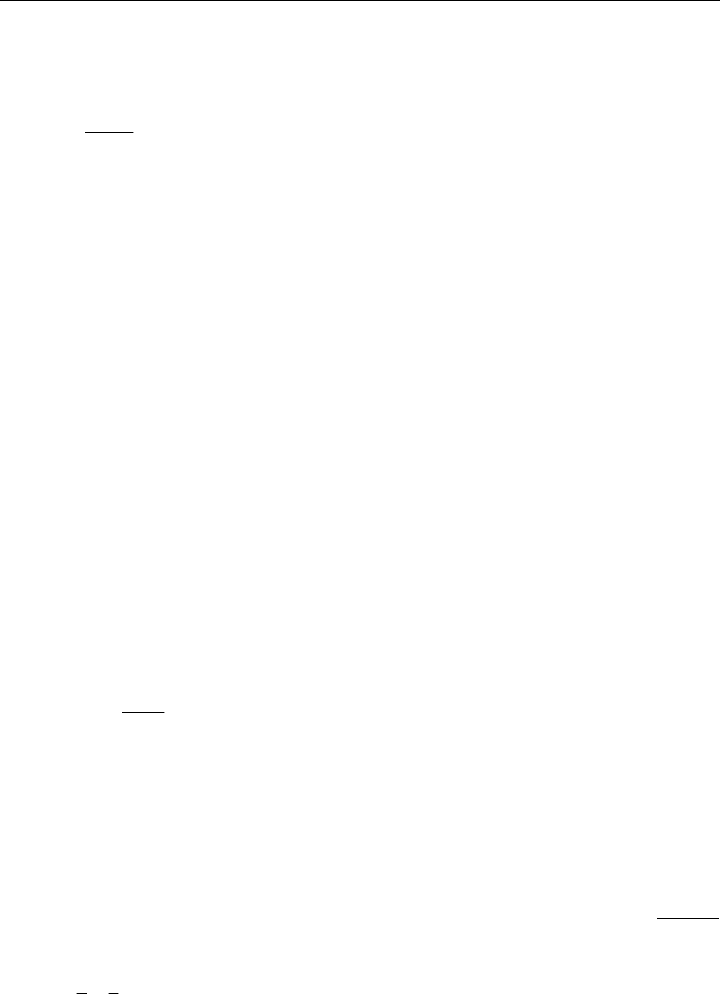
5 Das Konzept der Finite-Element-Methode
62
die
Steifigkeitsmatrix
»
»
»
»
¼
º
«
«
«
«
¬
ª
2
22
3
y
L4sym.
L612
L2L6L4
L6-12-L6-12
L
JE
k (5.64)
des ebenen
Balken-Elements im x-, z-System.
5.4 Prinzipieller Verfahrensablauf
Nachdem jetzt beispielhaft die Massen- und Steifigkeitsmatrizen sowie die Lastvektoren für
drei Elementtypen bekannt sind, wollen wir uns der Ablauffolge von den Einzelelementen
zum Gesamtmodell zuwenden. Wir beschränken uns hierbei auf den linearen elastomecha-
nischen Fall, wohl wissend, dass der Algorithmus für den dynamischen Fall nur ent-
sprechend erweitert werden braucht.
5.4.1
Steifigkeitstransformation
Die zuvor hergeleiteten Steifigkeitsmatrizen gelten ausschließlich für das festgelegte lokale
(elementeigene) Koordinatensystem des betrachteten
Stab- und Balken-Elements. In Struktu-
ren eingebaut werden aber diese Elemente beliebige Lagen einnehmen, weshalb für eine Ge-
samtaussage dann nur transformierte Steifigkeiten maßgebend sind. Diesen Zusammenhang
kann man sich sehr anschaulich an dem einfachen
Stab-Element klarmachen, für das die lo-
kale Kraft-Steifigkeits-Verschiebungs-Beziehung
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
2
1
2x
1x
u
u
11
11
L
AE
F
F
lautete. Die Elementsteifigkeit verknüpft dabei die Knotenkräfte mit den Knotenverschie-
bungen in Wirkrichtung. Kommt ein Element anders zu der Wirkrichtung „zu liegen“, so
wird auch die Steifigkeit anders sein.
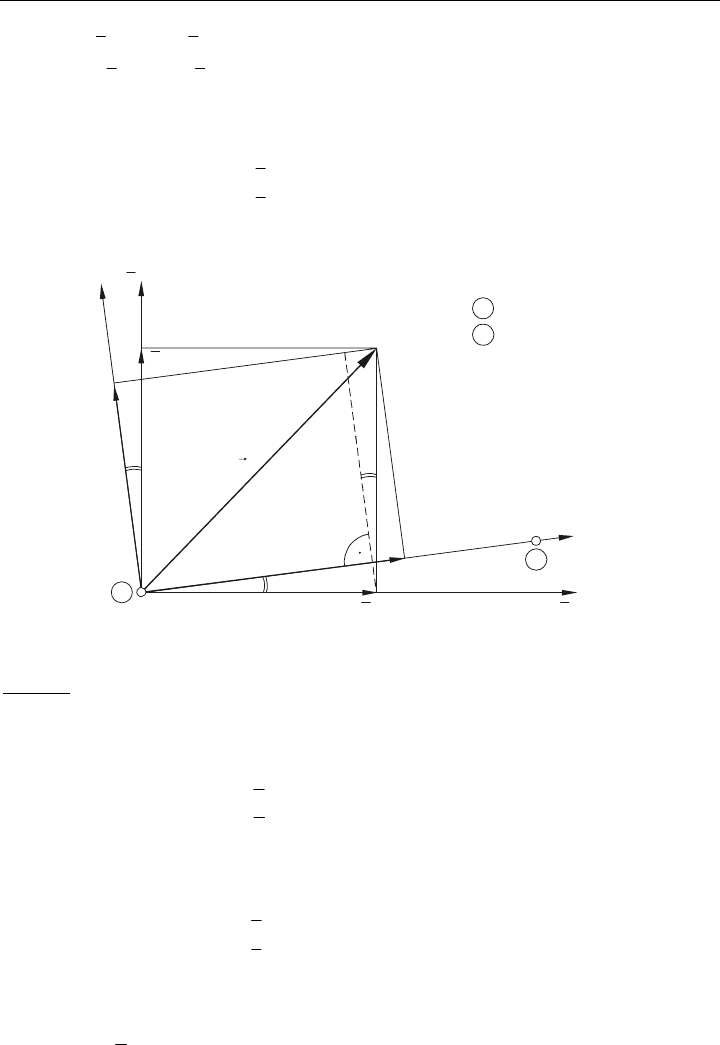
Um diesen Sachverhalt wieder allgemein gültig beschreiben zu können, betrachten wir das
Transformationsproblem eines Vektors. Der Vektor steht stellvertretend für eine Kraft oder
eine Verschiebung. Die durchzuführende Vektortransformation ist exemplarisch im Bild 5.8
dargestellt.
Der hierin abgebildete ebene Vektor v soll nun global-lokal transformiert werden, d. h. vom
globalen
x -, y -Koordinatensystem in das lokale x-, y-Koordinatensystem.
Die entsprechenden Vektorkomponenten sind demgemäß
5.4 Prinzipieller Verfahrensablauf
63
Į,cosvĮsinvv
Į,sinvĮcosvv
yxy
yxx
zweckmäßiger ist es aber, diese Gleichung matriziell anzugeben als
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
DD
D
»
¼
º
«
¬
ª
y
x
y
x
v
v
cossin
sinĮcos
v
v
. (5.65)
D
D
D
y
y
v
y
v
v
x
v
x
v
x
y
x
j
i
i
j
= Elementknoten
Bild 5.8:
Global-lokale Transformation eines Knotenvektors
Wir wollen diese Transformationsbeziehung nun übertragen auf die hier interessierenden
Knotengrößen
Kraft und Verschiebung, die sich somit ergeben zu
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
yi
xi
yi
xi
F
F
ĮcosĮsin
ĮsinĮcos
F
F
(5.66)
und
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
DD
DD
»
¼
º
«
¬
ª
i
i
i
i
v
u
cossin
sincos
v
u
. (5.67)
Diese beiden Matrizengleichungen können auch symbolisch geschrieben werden als
pTp
i
(5.68)
und

5 Das Konzept der Finite-Element-Methode
64
dTd
i
. (5.69)
Weil hierin aber nur ein Knoten zusammengefasst ist, muss die
Transformationsmatrix für
ein Element erweitert werden zu
»
»
»
»
¼
º
«
«
«
«
¬
ª
ĮcosĮsin00
ĮsinĮcos00
00ĮcosĮsin
00ĮsinĮcos
T . (5.70)
Eine wichtige Eigenschaft dieser
Transformationsmatrix ist die Gleichheit der inversen
Transformierten zur transponierten Transformierten:
t1
TT
. (5.71)
Diese Aussage kann bestätigt werden aus der
Invarianz der äußeren Arbeit, die als skalare
Größe in allen Koordinatensystemen gleich sein muss. Daher kann angesetzt werden:
dpdp
tt
a
W. (5.72)
Berücksichtigt man hierin die Transformationsbeziehung, so darf auch
dTTpdTpTdp
tt
t
t
. (5.73)
geschrieben werden. Wegen der uneingeschränkten Gültigkeit der Arbeitsaussage muss so-
mit
ITT
t
(5.74)
also gleich der Einheitsmatrix sein, was Aussage der Gl. (5.71) war. Unter Nutzung der bis-
herigen Beziehungen wollen wir jetzt die Transformation der Elementsteifigkeitsmatrix vor-
nehmen. Dazu gehen wird von der finiten Gleichung
dkp (5.75)
aus und führen darin Gl. (5.68) und (5.69) als Transformationen ein, es folgt hieraus
dTkpT (5.76)
und nach zusätzlicher Linksmultiplikation mit der transponierten Transformierten
dTkTpTT
tt
(5.77)
bzw. mit Gl. (5.74)

5.4 Prinzipieller Verfahrensablauf
65
dkp
erhält man die
transformierte Einzelsteifigkeitsmatrix
T
k
T
k
t
. (5.78)
Dies soll nunmehr beispielhaft an einem
Stab-Element gezeigt werden, welches dazu um
fiktive Knotenfreiheitsgrade
v
i
in y-Richtung erweitert wird:
dkp
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
2
2
1
1
2y
2x
1y
1x
v
u
v
u
0000
0101
0000
0101
L
AE
F
F
F
F
. (5.79)
Für die durchzuführende Transformation kürzen wir die Koeffizienten der Matrix
*)
mit
c = cos D und s = sin D ab, somit ist folgende Rechnung erforderlich:
TkT
c
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
t
cs00
sc00
00cs
00sc
0000
0101
0000
0101
cs00
sc00
00cs
00sc
.
Dies führt zu
»
»
»
»
»
¼
º
«
«
«
«
«
¬
ª
22
22
22
22
scsscs
csccsc
scsscs
csccsc
L
AE
k
. (5.80)
Würde man ein
Stab-Element jetzt um D = 90° drehen, so wäre das Ergebnis von Gl. (5.80),
dass die Elementsteifigkeit dann in y-Richtung umorientiert wäre.
5.4.2 Äquivalente Knotenkräfte
Bei den vorherigen Betrachtungen ist schon deutlich geworden, dass die an einem finiten
Modell angreifenden Kräfte über die Knoten eingeleitet werden sollten. Diesbezüglich ist
anzustreben, dass die Knoten immer so platziert werden, dass sie unterhalb der
Kraftangriffspunkte zum Liegen kommen. Falls dies nicht möglich ist, müssen gemäß Gl.
(5.11) und Gl. (5.48) die angreifenden Kräfte auf
alle Knotenfreiheitsgrade verschmiert
werden. Dafür gilt es, das folgende Prinzip zu wahren:
*)
Anmerkung:
c
kck
5 Das Konzept der Finite-Element-Methode
66
Alle nicht an einem Knoten eines finiten Elementes angreifenden Kräfte müssen so auf
die Freiheitsgrade verteilt werden, dass die angreifenden Kräfte mit ihren Verschie-
bungen dieselbe virtuelle Arbeit leisten, wie die Knotenkräfte mit ihren örtlichen Ver-
schiebungen.
Viele FE-Programme führen diese „Verschmierung“ automatisch durch.
Bezeichnen wir nun die
verschmierten Kräfte als äquivalente Kräfte
ä
p , so muss die virtu-
elle Arbeit folgendermaßen angesetzt werden:
³³
0
tt
V
t
ä
t
a
į0dįdVįįįW Fuqupupd . (5.81)
Wird hierin wieder der Verschiebungsansatz mit
ttt
į Gdu G
eingeführt, so gilt für die äquivalenten Knotenkräfte eines Elements
FGqGpGp
³³
t
t
0
t
V
ä
0ddV (5.82)
oder als Erkenntnis, dass das
Verschmieren jeweils durch Multiplikation mit dem Ansatz
durchgeführt wird, damit alle Freiheitsgrade angesprochen werden.
Diese Vorgehensweise wollen wir kurz am Stab- und Balken-Element demonstrieren.
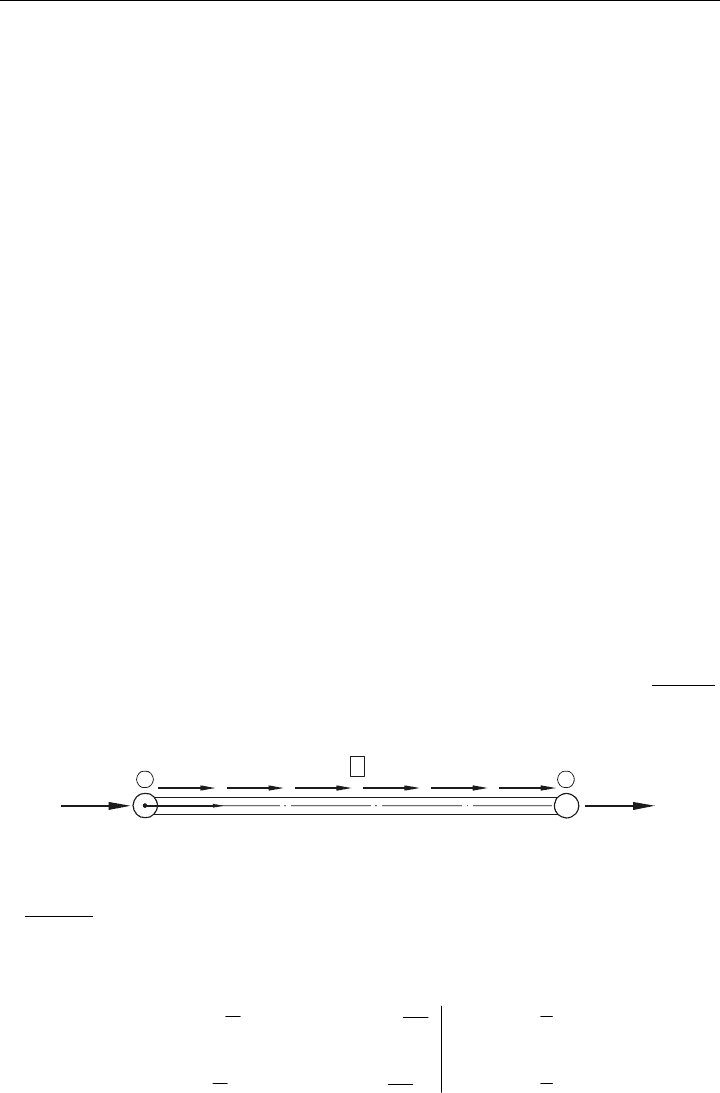
1-D-Stab-Element unter einer verteilten Längskraft (z. B. Eigengewicht) gemäß Bild 5.9.
Die äquivalenten Knotenlasten sind in Richtung der Freiheitsgrade anzutragen.
1 2
x
1
q
x
?F
x
ä1
?F
x
ä2
Bild 5.9: Äquivalente Knotenkräfte am Stab-Element
Aus dem übertragenen Ansatz von Gl. (5.82) folgt:
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
»
¼
º
«
«
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
³
2
1
2
1
Lq
o
L
L2
x
L2
x
x
qdxq
L
x
L
x
1
F
F
x
2
2
xx
L
o
x
ä2
x
ä1
ä
p
. (5.83)
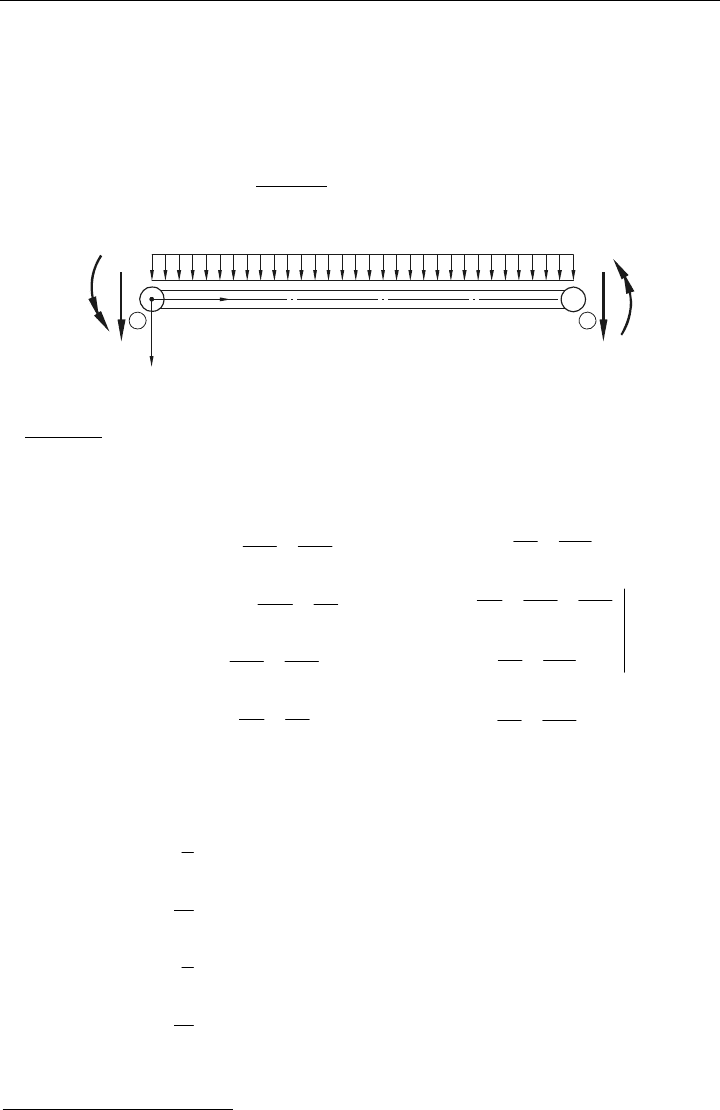
5.4 Prinzipieller Verfahrensablauf
67
Das formale Vorgehen führt hier auf eine Lösung, die natürlich auf der Hand lag. Aus ein-
facher Überlegung findet man sicherlich auch, dass die Kraft hälftig aufzuteilen ist.
Im nachfolgenden Fall ist dies jedoch nicht sofort ersichtlich.
2-D-Balken-Element unter einer verteilten konstanten Oberflächenkraft (z. B. Eigenge-
wicht oder Linienlast) gemäß Bild 5.10
F
1ä
z
F
2ä
z
z
1
2
x
q
z
M
1ä
y
M
2ä
y
Bild 5.10: Äquivalente Knotenkräfte am ebenen Balken-Element
Als Ansatz
*)
hierfür gilt
o
L
L4
x
L3
x
L2
x
L
x
L4
x
L3
x2
2
x
L2
x
L
x
x
qdxq
L
x
L
x
L
x2
L
x3
L
x
L
x2
x
L
x2
L
x3
1
M
F
M
F
2
43
3
4
2
3
2
432
3
4
2
3
zz
L
o
2
32
3
3
2
2
2
32
3
3
2
2
y
ä2
z
ä2
y
ä1
z
ä1
ä
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
¬
ª
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
¬
ª
³
p
oder
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
¬
ª
12
L
2
1
12
L
2
1
Lq
zä
p , (5.84)
*)
Anmerkung: Es müssen zu den Knotenfreiheitsgraden alle entsprechenden Knotenkräfte angetragen werden.
