Klein B. FEM: Grundlagen und Anwendungen der Finite-Element-Methode im Maschinen - und Fahrzeugbau
Подождите немного. Документ загружается.

3 Grundgleichungen der linearen Finite-Element-Methode
28
ia
WW G G (3.30)
wird.
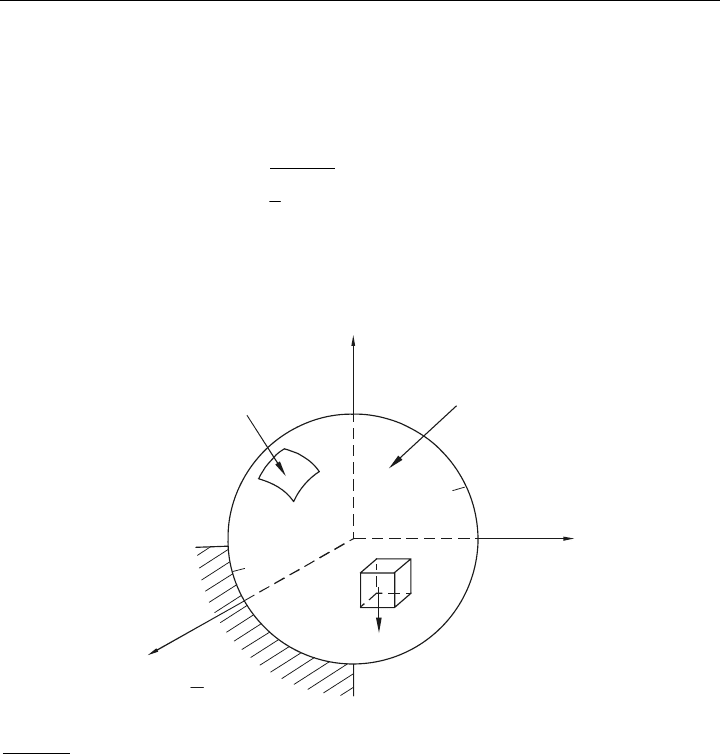
Um dieses Prinzip nun anwenden zu können, müssen wir die beschriebenen Arbeiten defi-
nieren. Dazu denken wir uns im Bild 3.4 einen beliebigen elastischen Körper. Die Ober-
fläche dieses Körpers soll nun so aufgeteilt werden, dass mit O
u
ein Verschiebungsrand für
vorgeschriebene Verschiebungen
u und mit O
V
ein Spannungsrand für gegebene Kräfte q
(verteilte Oberflächenlasten) und
F (konzentrierte Einzellasten) vorliegen. Im Inneren sollen
noch Volumenkräfte
p (Eigengewicht, Fliehkräfte o. Ä.) auftreten.
z
x
y
O
u
O
V
q
F
p
u
Oauf
uu
Bild 3.4: Zugelassene äußere Lasten an einem Körper
Die virtuelle Arbeit der äußeren Lasten kann dann folgendermaßen angesetzt werden:
0dįdVįįįW
0
t
V
tt
a
qupuFu
³³
. (3.31)
Hierzu korrespondiert die innere virtuelle Arbeit
dVįW
t
V
i
ıİ G
³
. (3.32)
Gemäß Gl. (3.30) sollen die Arbeiten gleichgesetzt werden, was zu der Identität
G
³
dV
t
V
ıİ G 0dįdVį
t
0
t
V
t
qupuFu
³³
(3.33)

3.4 Finites Grundgleichungssystem 29
führt. Die uns bekannten Beziehungen für die Verzerrungen
uDİ
bzw. für die Transponierung der Verzerrungen
ttt
įį Duİ
und für die Spannungen
uDEİEı
wollen wir nun einführen.
Aus Gl. (3.31) wird dann
0dįdV+įįdVį
t
0
t
V
ttt
V
qupuFuuDEDu
³³³
. (3.34)
Da bisher noch keine Näherung benutzt worden ist, gilt die vorstehende Beziehung exakt,
wenn mit
u die tatsächlichen Verschiebungen benutzt werden. An dieser Stelle setzt aber
jetzt die Näherung der Finite-Element-Methode ein, in dem für die Verschiebungen eines
Elements ein Ansatz gemacht werden soll. Um diesen Schritt verständlich zu machen, soll in
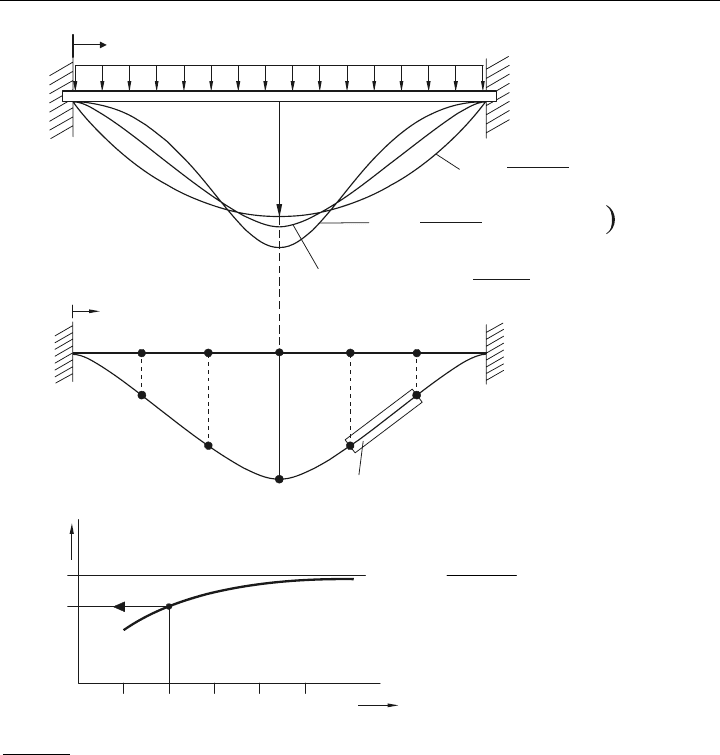
einem kleinen Exkurs das Biegeproblem in Bild 3.5
betrachtet werden.
Für den eingespannten Balken wollen wir hier per Approximation mit verschiedenen Funk-
tionen versuchen, die Biegelinie zu ermitteln. Man erkennt hierbei Folgendes:
Der Ansatz mit Kreisbogenform
1
w
ˆ
verstößt gegen die Zwänge der Randbedingung
und wird die Durchbiegung nur ungenau wiedergeben.
Durch die Wahl eines trigonometrischen Ansatzes
2
w
ˆ
kann zwar die Form der Biege-
linie abgeschätzt werden, jedoch ist auch hier die Durchbiegung noch sehr ungenau.
Mit einer Parabel 4. Grades
3
w
ˆ
kann sowohl die Form als auch der Betrag der Durch-
biegung recht gut abgeschätzt werden. Der Ansatz liegt auch sehr nahe an der „Ketten-
linie“.
Die Kettenlinie selbst ist eine Potenzfunktion 3. Grades, insofern bietet es sich an, einen
Approximationsansatz 3. Ordnung
4
w
ˆ
zu wählen.
Im Allgemeinen ist es so, dass mit einer Vergrößerung der Elementanzahl, d. h. Verfeine-
rung der Struktur, das Näherungsergebnis
w
ˆ
sich immer mehr der exakten Lösung w
nähert. Das gewählte Balkenbeispiel ist dafür kein schöner Beweis, da man mit zwei Ele-
menten (und
4
w
ˆ
) bereits eine sehr gute Lösung erhält, die sich kaum noch verbessern
lässt.
3 Grundgleichungen der linearen Finite-Element-Methode
30
q
w
x
n
246810
234
4
3
2
JE24
Lq
w
ˆ
[
[[
[
S
S
{
[S
D
cos
JE
Lq4
cosw
ˆ
5
4
02
w
ˆ
75 %
100 %
L/x
[
52416
JE384
Lq
w
ˆ
24
4
1
[[
JE384
Lq
w
exakt
01
2
2
3
34
xxxw
ˆ
DDDD
Bild 3.5:
Konvergenzverlauf einer Approximationsfunktion für Balkenbiegung
Auf dieser Erkenntnis aufbauend wollen wir uns wieder Gl. (3.34) zuwenden, in dem wir
jetzt einen Verschiebungsansatz von der Form
dGu (3.35)
einführen wollen. Mit diesem Ansatz wird also eine Verbindung zwischen beliebigen Ver-
schiebungen
u in einem Körper über bestimmte „Stützstellen“ d (Knotenverschiebungen)
hergestellt. Diese Verbindung wird über die Zeilenmatrix
G gebildet, die insofern also An-
satzfunktionen enthalten muss. Stellt man zu Gl. (3.35) noch die Variation
ttt
įį Gdu ,
auf, so kann nun Gl. (3.34) ausformuliert werden zu

3.4 Finites Grundgleichungssystem 31
³³³
V0
ttttttttt
V
0dįdV+įįdVį qGdpGdFGddGDEDGd ,
da dies für alle Variationen gelten muss, kann auch
³³³
0
t
V
t
t
V
0ddV
t
dV qGpGFGdGDEGD (3.36)
geschrieben werden. Analysiert man diese Gleichung, so stellt man fest, dass auf der linken
Seite das Produkt einer Steifigkeit mit einem Weg steht, welches auf der rechten Seite gleich
den äußeren Kräften ist. Je nach gewähltem Ansatz kann diese Gleichung nicht exakt erfüllt
werden. Für Gl. (3.36) wollen wir verkürzt
pdk
ˆ
. (3.37)
schreiben. Dies ist die gesuchte
finite Gleichung, in der die Knotenverschiebungen d über
die
Elementsteifigkeit k mit den gesamten äußeren Kräften p
ˆ
in Relation stehen. Als
Vorschrift zur Berechnung der Steifigkeitsmatrix haben wir
dVdV
t
V
t
V
BEBGDEGDk {
³³
(3.38)
erhalten. Die auf der rechten Seite von Gl. (3.36) stehenden Ausdrücke stellen insbesondere
Beziehungen dar, wie Kräfte auf die Knoten eines vernetzten Gebietes zu verteilen sind.
Zur Matrix der Ansatzfunktion
>@
!,g,g
21
t
G soll noch bemerkt werden, dass die hierfür
zu wählenden Glieder bevorzugt aus Polynomen konstruiert sind, wie beispielsweise
g g xg yg x g xyg y usw
12 3 4
2
56
2
1 ,,, , , .
Es ist leicht nachvollziehbar, dass diese Ausdrücke einfach zu integrieren und zu differenzie-
ren sind.
3.4.2 Methode von Galerkin
Ein andere Möglichkeit, die finite Gleichung zu finden, besteht in der Methode von Bubnov/
Galerkin oder allgemein in der Methode des gewichteten Restes. Von der Idee her wird eine
Differenzialgleichung genommen, in der für die Unbekannte ein Ansatz gemacht wird und
man für das Integral des Restes verlangt, dass es möglichst klein wird /BAT 86/.
Da wir es hier mit einem Grundprinzip zu tun haben, soll der mathematische Hintergrund
kurz betrachtet werden. Nehmen wir an
ruD (3.39)

3 Grundgleichungen der linearen Finite-Element-Methode
32
sei die differenzielle Formulierung eines physikalischen Problems. Hierin bezeichnet u die
unbekannte Zustandsgröße und r eine bekannte rechte Seite. Des Weiteren sollen noch mit
0uR
Bi
(3.40)
Randbedingungen vorgegeben sein. Die „gewichtete Restmethode“ geht nun davon aus, dass
sich die Lösung für Gl. (3.39) darstellen lässt als
¦
n
1i
ii
gau , (3.41)
wobei
a
i
Multiplikatoren und g
i
linear unabhängige Funktionen sind. Der Ansatz sollte hier-
bei mindestens die Randbedingungen erfüllen. Setzt man jetzt diesen Näherungsansatz in die
DGL ein, so wird wahrscheinlich eine absolute Identität der linken und rechten Seite nicht
zu erfüllen sein, sondern es wird mit
W
R
ein Restwert
0ruDW
R
z
(3.42)
übrig bleiben, den es in idealer Weise zu minimieren gilt. Nach der Methode von Galerkin
ist
³³
RandR
Bi
bereich
LösungsB
Ri
0dRRgdBWg (3.43)
also zu fordern. Wir wollen dies nunmehr übertragen auf die DGL des Gleichgewichts
(3.24), die vereinbarungsgemäß eine Matrizengleichung darstellt. Entsprechend des be-
schriebenen Formalismus multiplizieren wir diese DGL mit einer Ansatzfunktionsmatrix
G
t
und integrieren über das Volumen eines Körpers. Man erhält
0dV
t
t
V
³
puDEDG . (3.44)
Randbedingungen sind im vorliegenden Fall nicht zu berücksichtigen, weshalb das Problem
vollständig beschrieben ist. Später werden wir im Kapitel 11.2 bei der Behandlung von Wär-
meleitungsproblemen erkennen, dass für eine Lösung verschiedene Randbedingungen maß-
gebend sein können. Als Nächstes führt man in Gl. (3.44) den bekannten Ansatz
dGu
ein. Die Knotenverschiebungen sind somit nichts anderes, als die noch zu bestimmenden
Multiplikatoren und daher für uns die eigentliche Lösung des diskretisierten Problems.
Setzen wir jetzt den Ansatz in dieser Form ein, so folgt
0pGdGDEDG
³³
dVdV
t
V
t
t
V

3.4 Finites Grundgleichungssystem 33
oder besser zusammengefasst
0pGdGDEGD
³³
dVdV
t
V
t
V
. (3.45)
Man erkennt hierin die Analogie zu Gl. (3.36) und hat wieder die
finite Gleichung
pdk
ˆ
gefunden. Sollen zu den angesetzten Volumenkräften auch noch andere Kräftegruppen be-
rücksichtigt werden, so ist die rechte Seite der Gl. (3.45) um diese Kräfte geeignet zu ver-
vollständigen.
Zur Abrundung der Elastik soll die Galerkin’sche Methode auch noch auf die dynamische
Gleichgewichtsgleichung (3.27) angewandt werden. Aus
0puDEDu
t
ȡ
folgt dann wieder
³
¸
¹
·
¨
©
§
U
V
dV
tt
0puDEDuG
bzw. nach Einsetzen des Ansatzes
0pGdGDEGDdGG U
³³³
dVdVdV
V
t
t
V
t
V
. (3.46)
Dies ist gleichzusetzen mit der bekannten Schwingungsdifferenzialgleichung
0pdkdm
ˆ
. (3.47)
Für die neu auftretende Massenmatrix ist somit auch die Bildungsvorschrift
dVȡ
t
V
GGm
³
(3.48)
ermittelt worden.
34
4 Die Matrix-Steifigkeitsmethode
Ein vom Verständnis der Vorgehensweise guter Einstieg in die Finite-Element-Methode
stellt die von der Tragwerksberechnung her bekannte Matrix-Steifigkeitsmethode /HAH 75/
dar. Wie man später erkennen wird, ist der ablaufende Formalismus dem der FE-Methode
völlig identisch.
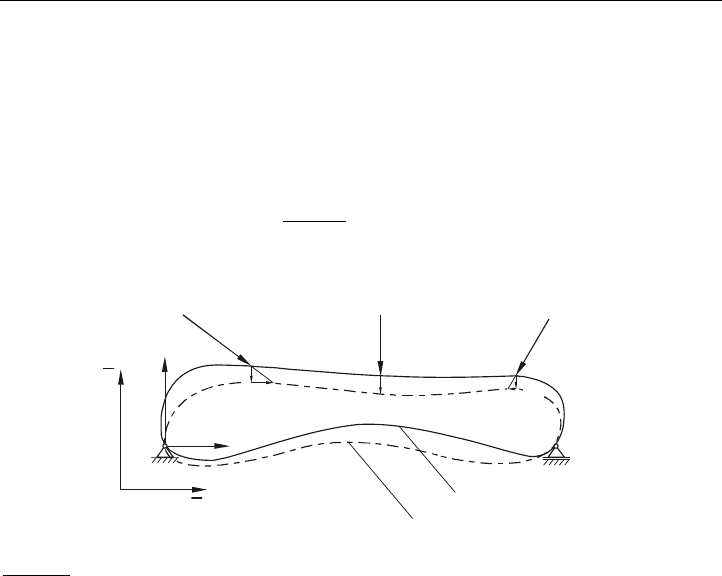
Zur Begründung der Theorie ist im Bild 4.1 ein beliebiges elastisches Tragwerk dargestellt.
Die einwirkenden äußeren Kräfte werden dieses Tragwerk verformen, sodass eine Durchsen-
kung festzustellen sein wird.
v
1
v
2
u
1
u
3
F
1
F
2
F
3
v
3
unverformter Körper
verformter Körper
y, v
x, u
y
x
Bild 4.1: Verformungszustand einer elastischen Tragkonstruktion
Bei unterstellten kleinen Verformungen und vorausgesetzter Linearität kann zwischen den
Kräften und den Verschiebungen folgender Zusammenhang angegeben werden:
Die Verschiebung
>@
ii
t
i
vu u von Körperpunkten hängt eindeutig von der Wirkung
aller Kräfte
i
F ab:
,
iii
Fuu i = 1, ..., n.
Im Fall der Linearität muss auch die Umkehrung gelten, und zwar gehört zu einem Ver-
formungszustand ein eindeutiger Kräftezustand:
iii
uFF i = 1, ..., n.
Hieraus ist zu folgern, dass die Kräfte über eine Steifigkeit mit den Verschiebungen linear
verknüpft sind, d. h. eine Beziehung
Fku
iij
j
n
i
¦
1
, i = 1, ..., n (4.1)
besteht. Entwickelt man weiter Gl. (4.1) als Matrizengleichungen, so gilt auch
4 Die Matrix-Steifigkeitsmethode
35
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
n
2
1
nn2n1n
n22221
n11211
n
2
1
u
u
u
kkk
kkk
kkk
F
F
F
#
"
###
"
"
#
. (4.2)
Die hierin auftretenden Koeffizienten
k
ij
heißen Verschiebungseinflusszahlen und sind nach
Maxwell symmetrisch, d. h. es gilt
k
k
ij ji
. Damit ist auch die Koeffizientenmatrix sym-
metrisch über die Hauptdiagonale.
Besonders vorteilhaft lässt sich die Matrix-Steifigkeitsmethode bei stabartigen Tragwerken
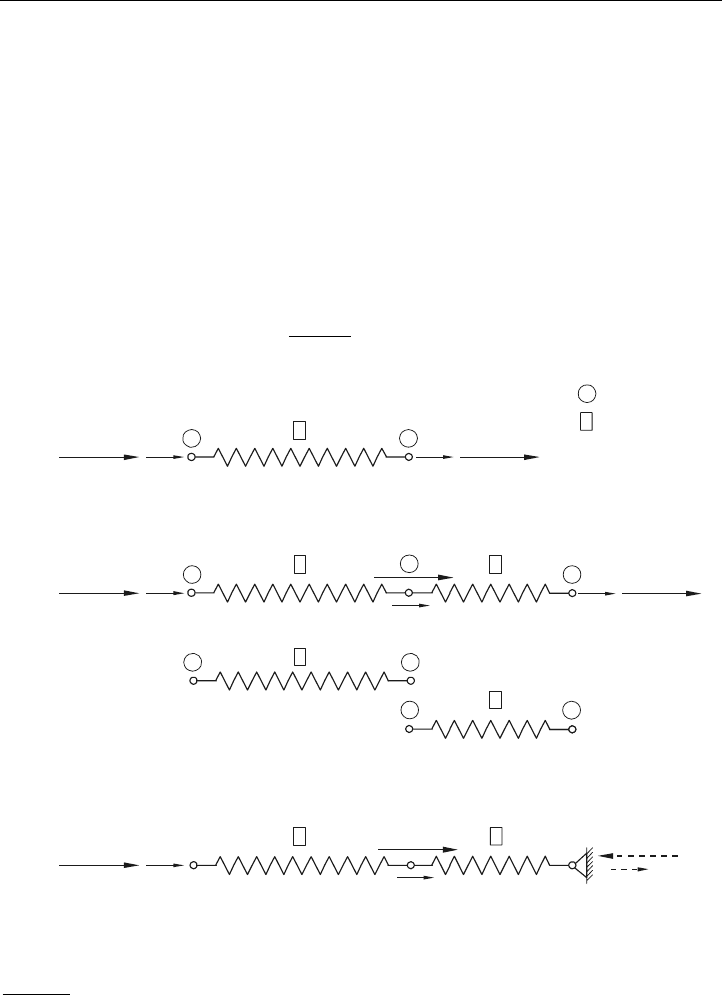
anwenden. Die prinzipielle Vorgehensweise soll hier aber für ein Federelement (Stabanalo-
gie) dargestellt werden, so wie es im Bild 4.2
eingeführt ist.
Knotenzähler
Elementzähler
F
1
u
1
F
1
u
1
F
1
u
1
F
2
F
3
u
2
F
2
u
2
F
2
u
2
F= F
R 3
u=0
3
u
3
c
1
c
2
c
1
1
1
1
2
2
2
2
1
1
1
1
2
2
2
3
3
a)
b)
c)
c
1
c
2
Bild 4.2: Vorgehensweise der Matrix-Steifigkeitsmethode (nach /HAH 75/) am
Federmodell
a) Ansatz für das lineare Federelement
b) Systemansatz für zwei Federelemente
c) gebundenes System
i
c Federkonstante;
wD8/dGc
3
i
4
ii

4 Die Matrix-Steifigkeitsmethode
36
Das Federelement repräsentiert dabei ein eindimensionales finites Element. Alle Informa-
tionen des Elements werden über die Knoten gegeben, die zufolge der Kräfte dann Verschie-
bungen ausführen. Auf Elementebene lässt sich somit formulieren:
.
,
12212
21121
ucucucF
ucucucF
'
'
(4.3)
Matriziell kann dies geschrieben werden als
ukp
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
2
1
2
1
u
u
cc
cc
F
F
. (4.4)
Die abgespaltene 2-x-2-Matrix k stellt hierbei die Elementsteifigkeitsmatrix einer Feder dar.
Will man hingegen die Beziehung für ein System entwickeln, so müssen so viele Glei-
chungen aufgestellt werden, wie Unbekannte vorhanden sind und die Randbedingungen be-
rücksichtigt werden. Im zu Grunde liegenden Beispiel soll ein System aus zwei Federn be-
trachtet werden, bei denen in zwei Knoten Kräfte eingeleitet werden und der dritte Knoten
festgehalten ist.
Die Systembeziehungen für die Kräfte lassen sich durch wechselseitiges Festhalten der
Knoten und die dann wirksame Federgleichung folgendermaßen entwickeln:
.0F,FF,ucF:0uu
;ucF,ucF,uccF:0uu
;0F,FF,ucF:0uu
31211132
223211221231
13232321
werden diese Gleichungen sortiert und zusammengefasst, so kann als Matrizengleichung
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
3
2
1
22
2211
11
3
2
1
u
u
u
cc0
cccc
0cc
F
F
F
bzw.
UKP (4.5)
angegeben werden. Die Gl. (4.5) drückt hierin den Systemzusammenhang aus, während Gl.
(4.4) als Elementgleichung aufgestellt worden ist.
An der Systemsteifigkeitsmatrix K ist zu erkennen, dass diese ebenso symmetrisch ist wie
die beiden zusammengefassten Elementmatrizen. Weiterhin ist an der Matrix zu erkennen,
dass diese auch sofort durch Blockaddition (direkte Steifigkeitsmethode = Überlagerung am
gemeinsamen Knoten) darstellbar wäre. Dies ist eine besondere Eigenart von Systemen, die
aus eindimensionalen Elementen (Stäbe, Balken) aufgebaut sind.
4 Die Matrix-Steifigkeitsmethode
37
Das vorstehende Gleichungssystem ist aber so nicht auflösbar, da die Randbedingungen bis-
her unberücksichtigt geblieben sind, d. h., das System kann insgesamt noch eine Starrkörper-
bewegung ausführen, was sich in der Singularität der Gesamtsteifigkeitsmatrix ausdrückt.
Ein Kennzeichen eines singulären Systems ist, dass die Determinante der Gesamtsteifig-
keitsmatrix
0ccccccccdet
2
2
1
2
212211
K
verschwindet. Erst für ein statisch bestimmtes System wird die Gleichung auflösbar, welches
durch eine positiv definite Gesamtsteifigkeitsmatrix möglich ist.
Wird nun in die vorstehende Gl. (4.5) die Randbedingung
u
3
0 eingearbeitet, so können
die Verschiebungen und die unbekannte Reaktionskraft
F
3
bestimmt werden:
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
0
u
u
cc0
cccc
0cc
F
F
F
2
1
22
2211
11
3
2
1
. (4.6)
Dazu muss das Gleichungssystem wie folgt aufgespalten werden:
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
2
1
211
11
2
1
u
u
ccc
cc
F
F
(4.7)
3
F =
>@
»
¼
º
«
¬
ª
2
1
2
u
u
c0 . (4.8)
Zufolge der beiden vorgegebenen Kräfte
FF
12
,
sollen jedoch zuerst die Verschiebungen be-
stimmt werden, und zwar aus der folgenden Rechnung:
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
2
1
22
221
1
2
1
F
F
c
1
c
1
c
1
c
1
c
1
u
u
PKU . (4.9)
Für die Inversion
1
K ist hierbei die Gleichung im Anhang benutzt worden. Aus der Aus-
multiplikation der vorstehenden Gleichung ergeben sich so für die Knotenverschiebungen
.F
c
1
F
c
1
u
,F
c
1
F
c
1
c
1
u
2
2
1
2
2
2
2
1
21
1
¸
¸
¹
·
¨
¨
©
§
(4.10)
Damit kann weiter die Reaktionskraft bestimmt werden zu
