Klein B. FEM: Grundlagen und Anwendungen der Finite-Element-Methode im Maschinen - und Fahrzeugbau
Подождите немного. Документ загружается.


5 Das Konzept der Finite-Element-Methode
48
K
2
1
0
2
1
2
1
2221
1211
2
1
2221
1211
F
F
P
P
u
u
kk
kk
u
u
mm
mm
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
. (5.8)
Aus Gl. (5.6) sind insbesondere die Vorschriften zu entnehmen, wie die entsprechenden
Matrizen oder Vektoren zu bilden sind, und zwar
die
Koeffizienten der Elementmassenmatrix m als
³
U
L
o
ijji
dxggAm , j, i = 1, 2 (5.9)
die
Koeffizienten der Elementsteifigkeitsmatrix k als
³
c
c
L
o
ijji
dxggAEk
, j, i = 1, 2 (5.10)
die
Knotenkomponenten des Oberflächenlastvektors
0
p
³
L
o
xjj
dxpgp , j = 1, 2
*)
(5.11)
der
Knotenlastvektor
»
¼
º
«
¬
ª
2
1
K
F
F
p
(5.12)
mit den
Randbedingungen
.
,
L
2
1i
i
i
22x
0
2
1i
i
i
11x
u
x
xg
1AENF
u
x
xg
1AENF
¸
¸
¹
·
¨
¨
©
§
w
w
{
¸
¸
¹
·
¨
¨
©
§
w
w
{
¦
¦
(5.13)
Wählt man für das
Stab-Element jetzt lineare Formfunktionen (shape functions) der Art
L
x
gund
L
x
1g
21
,
so gilt für den Verschiebungsansatz (s. Gl. (5.4))
*) Anmerkung: Zur Gl. (5.11) ist anzumerken, dass der Ausdruck eine Vorschrift enthält, wie verteilte Lasten
- die zwischen Knoten eingeleitet werden - bezüglich der Formfunktionen konsistent auf die
Knoten zu verschmieren sind. Die Gl. (5.13) wird vielfach nicht berücksichtigt.
5.3 Mathematische Formulierung
49
ttt,
21
u
L
x
u
L
x
1xu
¸
¹
·
¨
©
§
, (5.14)
womit die Verschiebungs- und Kraftrandbedingungen erfüllt werden. Der Verlauf dieser An-
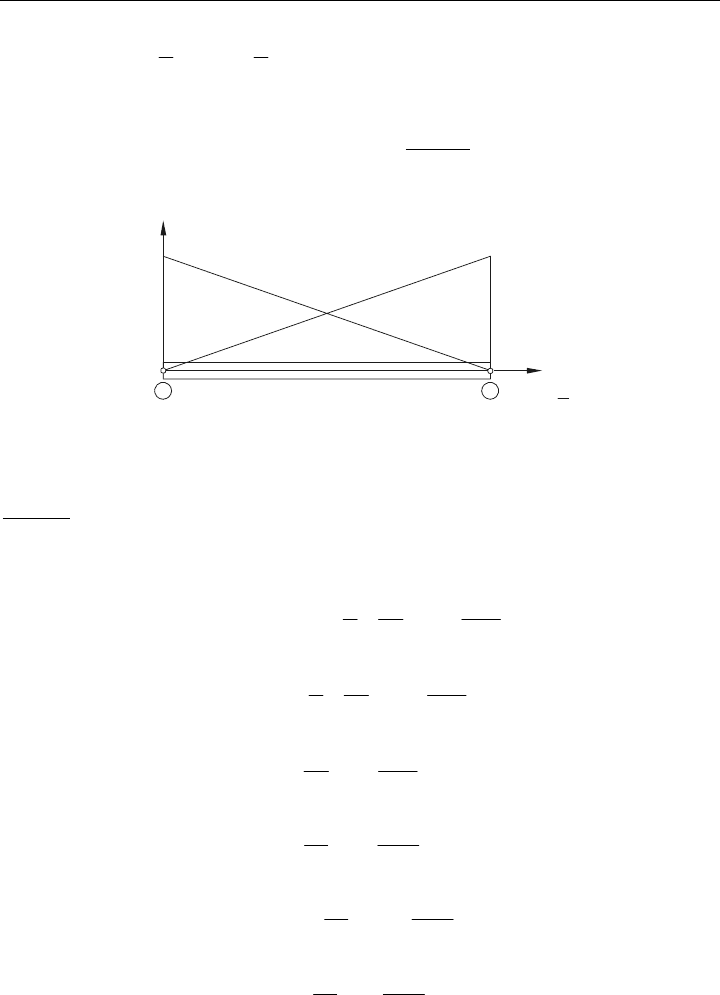
satzfunktionen über die normierte Stablänge zeigt Bild 5.4
zu einem beliebigen Zeitpunkt
bzw. in den Knoten.
1 2
g
[
1g
1
[
2
g
L
x
[
)(u),0(u
1
tt
)(u),L(u
2
tt
Bild 5.4: Formfunktionen für das Stab-Element mit normierter Länge
Somit ist es jetzt möglich, die Koeffizienten der interessierenden Matrizen
³³
³³
³³
³³
³³
³³
c
c
c
c
c
c
U
U U
U
¸
¸
¹
·
¨
¨
©
§
U U
U
¸
¸
¹
·
¨
¨
©
§
U U
L
o
2
2
L
o
222
L
o
2
2
L
o
121
L
o
2
1
L
o
111
L
o
2
2
2
L
o
222
L
o
2
2
2
L
o
121
L
o
2
2
1
L
o
111
L
AE
dx
L
1
AEdxggAEk
L
AE
dx
L
1
AEdxggAEk
L
AE
dx
L
1
AEdxggAEk
L
3
A
dx
L
x
AdxggAm
L
6
A
dx
L
x
L
x
AdxggAm
L
3
A
dx
L
x
L
x
21AdxggAm
,
,
,
,
,
zu berechnen. Werden diese nun eingesetzt, so können die Matrizen ausformuliert werden zu

5 Das Konzept der Finite-Element-Methode
50
»
»
»
»
¼
º
«
«
«
«
¬
ª
3
1
6
1
6
1
3
1
LAȡm
(5.15)
und
»
¼
º
«
¬
ª
11
11
L
AE
k . (5.16)
Des Weiteren findet man für die Kraftvektoren
0
x
x
0
2
1
0
2
Lp
2
Lp
P
P
»
»
»
¼
º
«
«
«
¬
ª
{
»
»
¼
º
«
«
¬
ª
p (5.17)
und
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
ww
w
w
{
»
»
»
¼
º
«
«
«
¬
ª
2
1
L
2
L
1
0
2
0
1
K
2
1
K
u
u
dx
g
dx
g
dx
g
dx
g
AE
F
F
p , (5.18)
womit wieder das Gleichgewicht zu den Schnittgrößen
N
j
in den Knoten deutlich wird.
5.3.2 Ebenes Dreh-Stab-Element
Eine schöne Anwendung in der Physik bzw. Schwingungstechnik findet das (modifizierte)
Stab-Element, um Drehschwingungen analysieren zu können. Typische Fragestellungen er-
geben sich bei verzweigten Wellensystemen im Getriebebau oder bei Verarbeitungs-
maschinen.
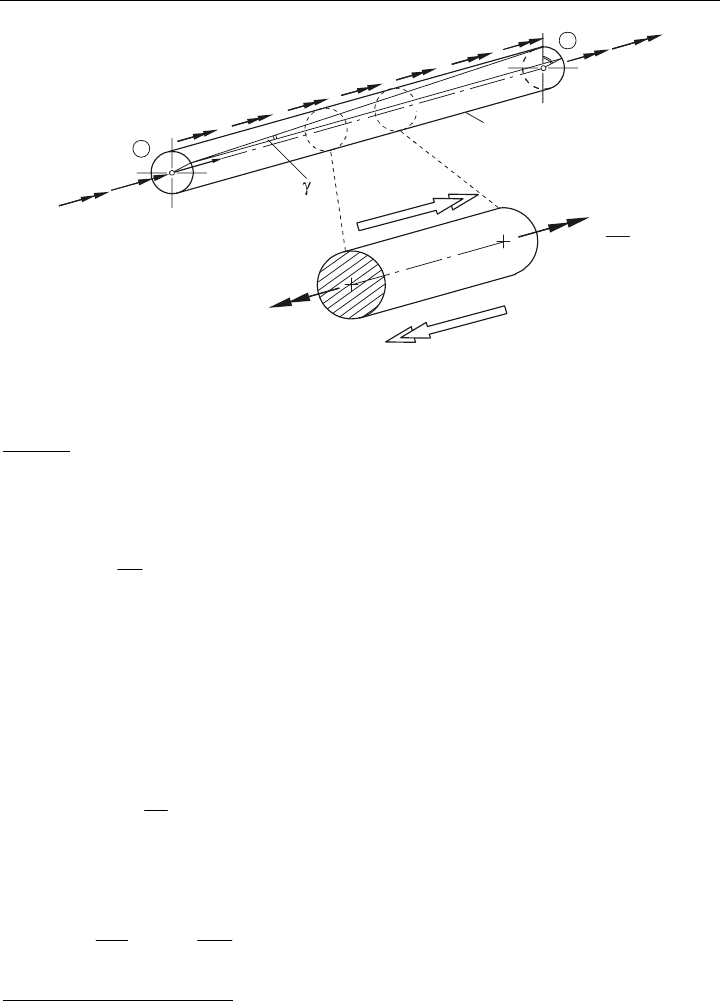
Um die zugehörigen Beziehungen für rotatorische Schwingungen aufstellen zu können, ist
im Bild 5.5
ein spezielles Drehstab-Element eingeführt worden. Hier ist weiter ange-
nommen, dass über die Länge des Elementes ein verteiltes Drehmoment
t
m eingeleitet wird.
Dies entspricht in etwa der Krafteinleitung über eine Nabe, Flansch etc.
An den Knoten soll das Element äußere Momente über die Einzelmomente
i
T weiterleiten
können, bzw. es werden diskrete Verdrehungen
i
ĭ
hervorgerufen. Für alle Zusammenhänge
sei linear elastisches Verhalten angenommen.
Angemerkt sei noch, dass die Massenträgheit um die x-Achse zu bilden ist (d. h. nicht wie
bei allgemeiner Kinematik als Massentensor).
5.3 Mathematische Formulierung
51
1
2
dx
dx
x
T
T
w
w
dxm
t
LJG
p
,
I
,
x
2
T
1
T
T
),x(m
t
t
I
dĬ
22
ĭ,ĭ
11
ĭ,ĭ
Bild 5.5: Mechanik des linearen Drehstab-Elements
*)
Bildet man jetzt unter den gezeigten Verhältnissen an einem infinitesimalen Elementchen
das Gleichgewicht, so folgt hieraus
.0dxmdx
x
T
d
t
w
w
I4
(5.19)
Durch Einsetzen von
³³
U U 4
dV dA
p
22
dxJdxdArdmrd
für das Massenträgheitsmoment
**)
und der bekannten Beziehung
x
JGT
p
w
Iw
für das Drehmoment kann die vorstehende Gl. (5.19) umgeformt werden zu
0m
x
JGJ
t
2
2
p
2
2
p
w
Iw
w
Iw
U
t
. (5.20)
*)
Anmerkung: Vorstehend bezeichnet
I x einen beliebigen Drehwinkel an der Stelle x, aber
21
, ))
bezeichnen jeweils Verdrehungen an den Knoten.
**)
Anmerkung 1: Das Trägheitsmoment
p
J (für polar) kann so nur für einen Kreisquerschnitt gebildet wer-
den; verallgemeinert müsste
t
J benutzt werden.
Anmerkung 2: Bei Wellenelementen ist
p
J = (S d
4
)/32.
5 Das Konzept der Finite-Element-Methode
52
Wird hierauf wieder der Galerkin‘sche Formalismus angewandt, so erhält man die
Gleichung
³
¸
¸
¹
·
¨
¨
©
§
w
Iw
w
Iw
U
L
o
tj
2
2
jp
2
2
jp
0dxmg
x
gJGgJ
t
j = 1, 2. (5.21)
Da auch für das vorliegende Problem der Gleichungstyp (5.2) maßgebend ist, muss der mitt-
lere Term in bekannter Weise umgeformt werden zu
xx
g
JG
x
gJG
x
gJG
x
j
p
2
2
jpjp
w
Iw
w
w
w
Iw
¸
¸
¹
·
¨
¨
©
§
w
Iw
w
w
,
wird dies berücksichtigt, so erhält man die zu Gl. (5.21) äquivalente Gleichung
0
o
L
x
gJGdxmg
xx
g
JGgJ
jp
L
o
tj
j
p
2
2
jp
¸
¸
¹
·
¨
¨
©
§
w
Iw
¸
¸
¹
·
¨
¨
©
§
w
Iw
w
w
w
Iw
U
³
t
. (5.22)
Mittels des Rayleigh-Ritz-Ansatzes
tt,
i
2
1i
i
xgx ) I
¦
(5.23)
bzw. mit den entsprechenden Zeit- und Ortableitungen
i
2
1i
i
2
i
2
2
1i
i
2
2
dx
g
x
g )
w
w
Iw
w
)w
w
Iw
¦¦
,
tt
folgt auch für Gl. (5.22)
.2,1j,0
o
L
x
g
gJG
dxmgdx
x
g
x
g
JGggJ
i
2
1i
i
jp
L
o
tj
2
1i
L
o
i
i
j
p
2
i
2
ijp
)
¸
¹
·
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
)
w
w
w
w
w
)w
U
¦
³
¦
³
t
(5.24)
Damit liegt wieder die diskretisierte DGL
K0
mmĭcĭĬ
(5.25)
vor, die entwickelt lautet:
K
2
1
0
2
x
1
x
2
1
2221
1211
2
1
2221
1211
T
T
T
T
cc
cc
»
»
¼
º
«
«
¬
ª
»
»
¼
º
«
«
¬
ª
»
»
¼
º
«
«
¬
ª
)
)
»
»
¼
º
«
«
¬
ª
»
»
¼
º
«
«
¬
ª
)
)
»
»
¼
º
«
«
¬
ª
44
44
. (5.26)
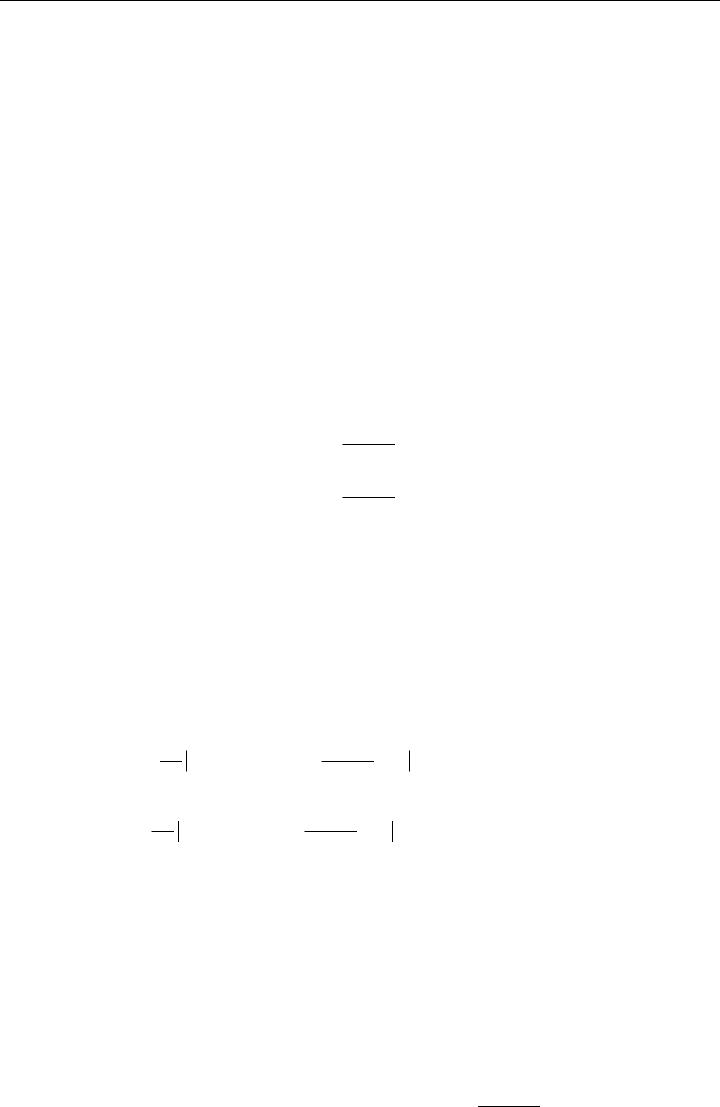
5.3 Mathematische Formulierung
53
Alle Berechnungsvorschriften für die benötigten Ausdrücke findet man wieder in Gl. (5.24),
und zwar
für die
Koeffizienten der Elementträgheitsmatrix
³
U
L
o
ijpji
dxggJĬ , j, i = 1, 2, (5.27)
für die
Koeffizienten der Elementdrehsteifigkeitsmatrix
³
c
c
L
o
ijpji
dxggJGc
, j, i = 1, 2, (5.28)
für den
Oberflächenlastvektor eines verteilten Momentes
0
t
t
0
L
o
t2
L
o
t1
0
2
x
1
x
0
2
Lm
2
Lm
dxmg
dxmg
T
T
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
»
¼
º
«
«
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
³
³
m (5.29)
und für den
Knotenlastvektor von eingeleiteten Momenten
K
2
1
K
T
T
»
¼
º
«
¬
ª
m
(5.30)
mit den
Randbedingungen
.
,
L
2
1i
i
i
pLp2
0
2
1i
i
i
p0p1
x
xg
JG
x
JGT
x
xg
JG
x
JGT
¸
¸
¹
·
¨
¨
©
§
)
w
w
w
wI
¸
¸
¹
·
¨
¨
©
§
)
w
w
w
wI
¦
¦
Da das
Dreh-Stab-Element auch wieder linear mit den gleichen Ansatzfunktionen wie in Gl.
(5.14) angesetzt werden kann, ergeben sich zu Gl. (5.15) und (5.16) ähnliche Matrizen.
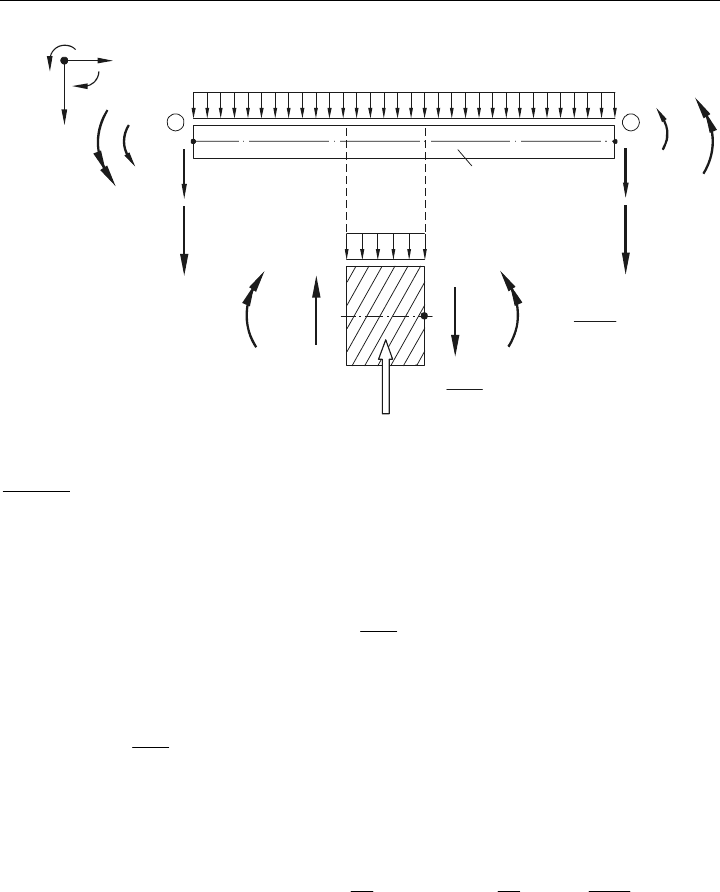
5.3.3 Ebenes Balken-Element
In Analogie zu den stabartigen Elementen soll nun das
Balken-Element beschrieben werden.
Wir wollen hierbei die Bernoulli-Hypothese zu Grunde legen, die unter reiner Biegung von
Schubverzerrungsfreiheit und gerade bleibenden Querschnitten ausgeht. Die im allgemeinen
Fall auftretenden Verhältnisse bei schlanken Elementen zeigt Bild 5.6
.
5 Das Konzept der Finite-Element-Methode
54
U
, E J , L
y
.
q dx
z
.
1
2
P
x
z,w
q (x, )
z
t
M
1
M
2
M
y
M
dM
dx
dx
y
y
U
Awdx
w'
1
Q
2
Q
z
Q
dx
dx
dQ
Q
z
z
11
Ȍ,Ȍ
22
Ȍ,Ȍ
Ȍ
22
w,w
11
w,w
Bild 5.6: Mechanik des Biege-Balken-Elements
Zur Ermittlung der beschreibenden Differenzialgleichung soll wieder von der Gleichge-
wichtsgleichung an einem Balken-Elementchen ausgegangen werden:
0dxqdx
dx
dQ
QdxwAQ:0K
z
z
zzz
U
¦
, (5.31)
dies führt zu der DGL
0q
dx
dQ
wA
z
z
U
. (5.32)
Hierin gilt es aber noch, die Ableitung der Querkraft durch die Verschiebung zu ersetzen.
Dazu kann noch die Momentenbedingung
0dx
dx
dM
M
2
dx
dxwA
2
dx
dxqdxQM:0M
y
yzzyp
U
¦
(5.33)
ausgenutzt werden. Vernachlässigt man dabei alle kleinen Größen zweiter Ordnung, so führt
dies auf die Beziehung
s
cc
yzyz
MQoderMQ.

5.3 Mathematische Formulierung
55
Unter weiterer Berücksichtigung der Biegelinienbeziehung
wJEM
yy
c
c
folgt aus Gl.
(5.33) also
IV
yz
wJEQ
c
. (5.34)
Wird diese Gleichung nun vorstehend eingeführt, so erhält man als DGL der Biegeschwin-
gung
0qwJEwA
z
IV
y
U
. (5.35)
Auf diese DGL wird jetzt wieder das Galerkin-Verfahren angewandt, wodurch folgendes
Funktional entsteht:
0dxqgwgJEwgA
L
o
zj
IV
jyj
U
³
, j = 1, ..., 4. (5.36)
Zur Erniedrigung der Ordnung des mittleren Terms gilt es wie zuvor schon, die Produktregel
anzuwenden, und zwar zunächst folgendermaßen:
wgJEwgJEwgJE
x
jy
IV
jyjy
ccc
c
ccc
w
w
,
wgJEwgJEwgJE
jyjy
IV
jy
ccc
c
c
ccc
. (5.37)
Diese Ordnungserniedrigung ist so lange durchzuführen, bis die Durchbiegung w in der
zweiten Ordnung vorliegt, also ist die Produktregel noch einmal anzuwenden auf
wgJEwgJEwgJE
jyjyjy
cc
s
c
cc
c
ccc
c
.
Damit kann jetzt folgende Ersetzung des Terms vorgenommen werden:
wgJEwgJEwgJEwgJE
jyjyjy
IV
jy
cc
s
c
cc
c
c
ccc
. (5.38)
Wird dies in Gl. (5.36) berücksichtigt, so liegt das Funktional in der Form
>
@
0
o
L
wgJE
wgJEdxqgwgJEwgA
jy
jy
L
o
zjjyj
cc
c
ccc
cc
s
U
³
(5.39)
vor. Es ist im Weiteren jedoch zweckmäßig, von folgender Gleichung auszugehen:

5 Das Konzept der Finite-Element-Methode
56
>@
.
o
L
wgwgJEdxqgdxwgJEwgA
jjy
L
o
zj
L
o
jyj
ccc
cc
c
cc
s
U
³³
(5.40)
Für die Verschiebungen soll jetzt wieder der zuvor schon benutzte Ansatz gemacht werden,
und zwar
,, tt
¦
4
1i
ii
dxgxw (5.41)
worin der
Knotenverschiebungsvektor sich folgendermaßen zusammensetzt:
»
»
»
»
¼
º
«
«
«
«
¬
ª
\
\
»
¼
º
«
¬
ª
2
2
1
1
2
1
w
w
d
d
d
.
*)
(5.42)
Führt man den Ansatz mit seinen Ableitungen
ii
4
1i
ii
4
1i
ii
4
1i
dgw
dgw
dgw
ccc
s
cc
¦
¦
¦
'''
,
,
ein, so ergibt sich
>@
.,,, 41jd
0
L
ggggJEdxqg
ddxggJEddxggA
L
o
i
4
1i
ijijyzj
i
4
1i
L
o
ijyi
4
1i
L
o
ij
"
s
c
s
c
¸
¸
¹
·
¨
¨
©
§
s
s
¸
¸
¹
·
¨
¨
©
§
U
³
¦
¦
³
¦
³
(5.43)
Diese Gleichung stellt somit wieder die Schwingungs-DGL eines Balken-Elements dar:
K0
ppdkdm
. (5.44)
Umseitig ist diese Gleichung als matrizielle Elementbeziehung ausgeschrieben worden:
*)
Anmerkung:
>@
\\q arctan mit \
c
w

5.3 Mathematische Formulierung
57
K
2
2
1
1
0
2y
2z
1y
1z
2
2
1
1
44434241
34333231
24232221
14131211
2
2
1
1
44434241
34333231
24232221
14131211
M
Q
M
Q
M
Q
M
Q
w
w
kkkk
kkkk
kkkk
kkkk
w
w
mmmm
mmmm
mmmm
mmmm
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
<
<
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
<
<
»
»
»
»
¼
º
«
«
«
«
¬
ª
.
(5.45)
Die Vorschriften, wie die Matrizen und Vektoren zu bilden sind, sind ebenfalls wieder aus
Gl. (5.43) zu entnehmen. Von der Dimension (z. B. bei 3-D) her ist jede Matrize an die An-
zahl der Unbekannten anzupassen.
Damit kann ausformuliert werden, und zwar
für die Koeffizienten der Elementmassenmatrix findet man somit
dxggAm
i
L
o
jji
U
³
, j, i = 1, ..., 4, (5.46)
für die
Koeffizienten der Elementsteifigkeitsmatrix findet sich entsprechend
³
s
s
L
o
ijyji
dxggJEk , j, i = 1, ..., 4, (5.47)
die
Vektorkomponenten der Streckenlast als Knotengrößen ergeben sich zu
0
L
o
z4
L
o
z3
L
o
z2
L
o
z1
0
2y
2z
1y
1z
0
dxqg
dxqg
dxqg
dxqg
M
Q
M
Q
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
¬
ª
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
¬
ª
³
³
³
³
p (5.48)
und
die
Vektorkomponenten des Gleichgewichts an den Knoten zufolge angreifender Einzel-
lasten und Momente
