Klein B. FEM: Grundlagen und Anwendungen der Finite-Element-Methode im Maschinen - und Fahrzeugbau
Подождите немного. Документ загружается.

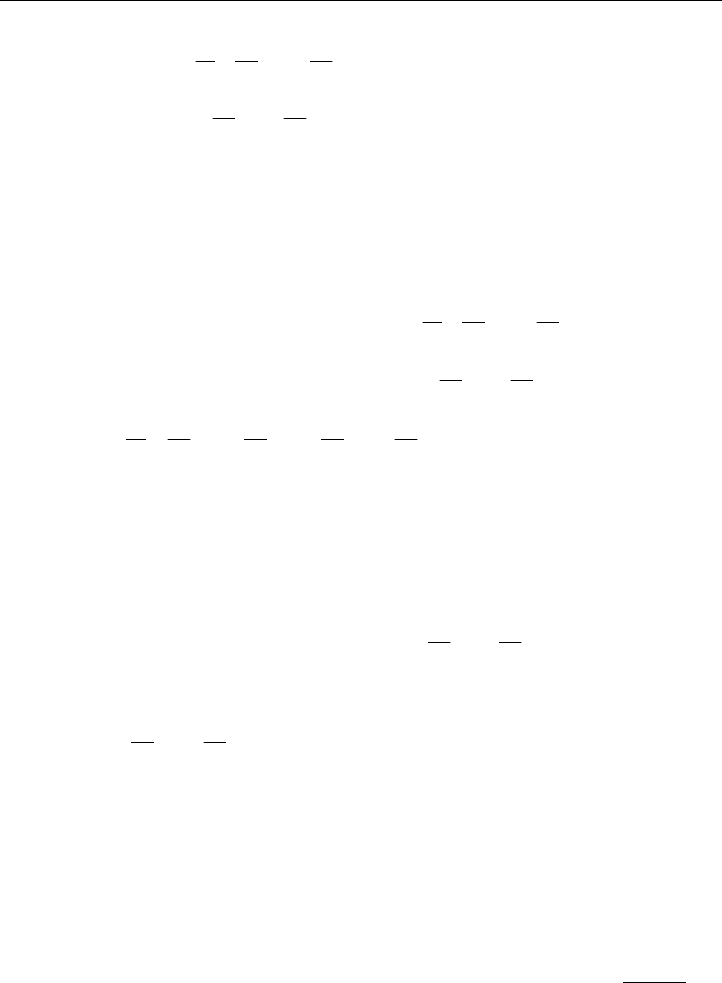
4 Die Matrix-Steifigkeitsmethode
38
>@
21
2
2
1
2
2
2
1
21
23
FF
F
c
1
F
c
1
F
c
1
F
c
1
c
1
c0F
»
»
»
»
»
¼
º
«
«
«
«
«
¬
ª
¸
¸
¹
·
¨
¨
©
§
. (4.11)
Manchmal sind auch die Schnittkräfte
ij
S im Element von Interesse. Für deren Bestimmung
gilt, dass diese stets auf Elementebene zu ermitteln sind, und zwar
im Element 1 für den Knoten c und d:
»
»
»
»
¼
º
«
«
«
«
¬
ª
¸
¹
·
¨
©
§
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
2
2
1
2
2
2
1
21
11
11
2
1
11
11
12
11
F
c
1
F
c
1
F
c
1
F
c
1
c
1
cc
cc
u
u
cc
cc
S
S
1112
12
2
1
1
2
1
2
2
1
1
21
111
SS
FF
c
c
F
c
c
F
c
c
F
c
1
c
1
cS
¸
¸
¹
·
¨
¨
©
§
(4.12)
bzw.
im Element 2 für den Knoten
d und e:
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
0
F
c
1
F
c
1
cc
cc
0
u
cc
cc
S
S
2
2
1
2
22
22
2
22
22
23
22
.
2223
212
2
1
2
222
SS
FFF
c
1
F
c
1
cS
¸
¸
¹
·
¨
¨
©
§
(4.13)
Die Erkenntnis aus diesem Beispiel soll im Weiteren sein, dass man durch die Anwendung
eines bestimmten Formalismus zu der Lösung einer bestimmten Klasse von Aufgaben
kommt. Verallgemeinert man diese Vorgehensweise, so lassen sich somit hinreichend kom-
plexe Tragwerke behandeln. Ziel muss es also sein, diesen methodischen Ansatz variabel zu
entwickeln.
Die algorithmische Verallgemeinerung soll jetzt an dem kleinen Tragwerk von Bild 4.3
wie
folgt vorgenommen werden:
Mit
>@
0FFF0
x4y3x3
t
a
F sollen die bekannten äußeren Kräfte bezeichnet wer-
den.
Entsprechend sollen mit
>@
x2y1x1
t
b
FFF F die Reaktionskräfte bezeichnet werden.
4 Die Matrix-Steifigkeitsmethode
39
Sinngemäß bezeichnet
>
@
44332
t
a
vuvuv U die unbekannten Verschiebungen
und
>@
211
t
b
uvu U die bekannten Randbedingungen (vorgeschriebene Auflagerver-
schiebungen oder Unbeweglichkeiten).
Gemäß diesen Vereinbarungen kann die vorherige Gl. (4.5) bzw. die neu zu erstellende
Systemgleichung folgendermaßen partitioniert werden:
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
»
¼
º
«
¬
ª
b
a
bbba
abaa
b
a
U
U
KK
KK
F
F
. (4.14)
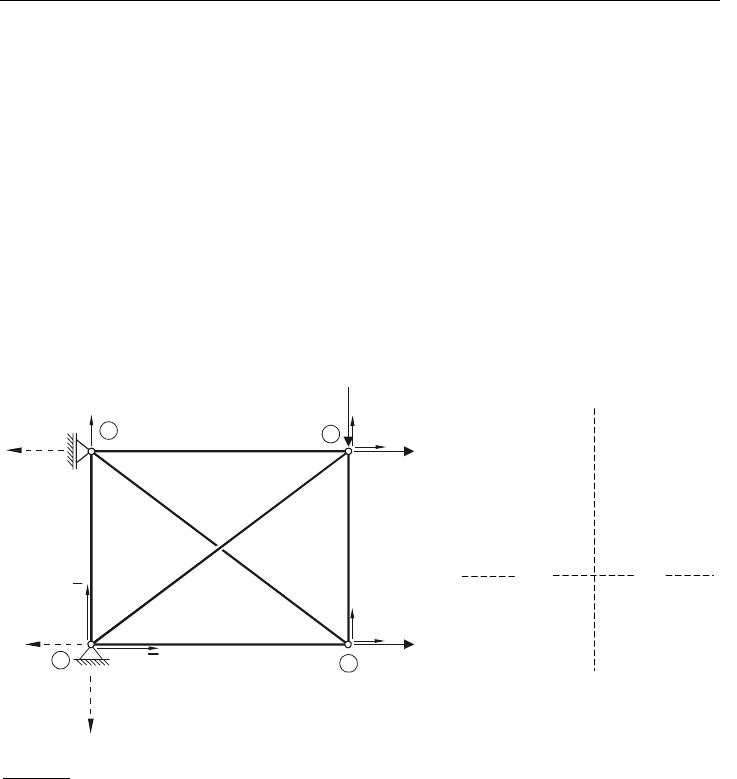
a) b)
1
2
3
4
F
2x
F
3x
F
3y
F
1y
F
1x
F
4x
v
3
v
2
v
4
u
3
u
4
y
x
Bild 4.3: Fachwerk aus Stab-Elementen (alle Knoten 2 FHGs)
a) Modell mit Kräften und Lager
b) beschreibendes Gleichungssystem
Wir haben es hier also mit einer Hypergleichung zu tun, in der mit
ba,
F ,
ba,
U Vektoren und
mit
aa
K ,
ab
K ,
bb
K Untermatrizen vorkommen. Löst man zum Zwecke der Komponenten-
bestimmung diese Gleichung auf, so folgt daraus
,UKUKF
babaaaa
(4.15)
.
bbbabab
UKUKF
(4.16)
Da die Verschiebungen interessieren, muss Gl. (4.15) aufgelöst werden nach
»
»
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
»
»
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
»
»
»
»
»
»
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
«
«
«
«
«
«
¬
ª
0u
0v
0u
v
u
v
u
v
F
F
F
0F
F
F
F
0F
2
1
1
4
4
3
3
2
bbba
abaa
x2
y1
x1
y4
x4
y3
x3
y2
KK
KK

4 Die Matrix-Steifigkeitsmethode
40
baba
1
aaa
UKFKU
(4.17)
und diese Gleichung zur Bestimmung der Reaktionskräfte in Gl. (4.16) eingesetzt werden,
man erhält so
bbbbaba
1
aabab
UKUKFKKF
. (4.18)
Bei den meisten technischen Systemen werden unbewegliche Auflager 0U
b
vorliegen;
für einen derartigen Fall vereinfachen sich die beiden vorstehenden Gleichungen zu
a
1
aaa
FKU
(4.19)
und
a
1
aabab
FKKF
. (4.20)
Der gezeigte Lösungsweg lässt sich nun formal folgendermaßen beschreiben:
Definition eines mechanischen Beschreibungselements (Stab oder Balken);
matrizielle Formulierung des Zusammenhangs zwischen Knotenkräften und Knotenver-
schiebungen; Erstellung einer Elementsteifigkeitsmatrix
k;
Zusammenbau der Gleichungen zu einem Gesamtkraftvektor P, einem Gesamtverschie-
bungsvektor
U und einer Gesamtsteifigkeitsmatrix K;
Unterdrückung der Starrkörperverschiebungen eines Systems durch die Einführung von
Randbedingungen und Partitionierung des Gleichungssystems in unbekannte Verschie-
bungen
a
U und unbekannte Reaktionskräfte
b
F ;
Lösung der entstandenen Teilgleichungssysteme und Ausweis der Verschiebungen
a
U
und der Reaktionskräfte
b
F
sowie
gegebenenfalls Rückrechnung zu den Schnittgrößen
S
ij
bzw. Spannungen ı in den Ele-
menten.
Von der Methodik des Vorgehens werden wir diese Schritte bei der im Weiteren zu be-
schreibenden FE-Methode alle wieder finden.

41
5 Das Konzept der Finite-Element-Methode
In den nachfolgenden Unterkapiteln soll das Konzept der FEM puzzleartig zusammengesetzt
werden, weshalb das Kapitel 5 grundlegend für das methodische Verständnis ist. Neben der
Darlegung des praktischen Vorgehens liegt der Fokus auf alternative mathematische Formu-
lierungen und letztendlich der Überführung in einen stringenten Gesamtablauf. Um die
Theorie möglichst transparent zu halten, werden nur Stab- und Balken-Elemente benutzt.
Dies vereinfacht zwar die Darstellung, beschränkt aber nicht die Allgemeingültigkeit der
Vorgehensweise. Insofern ist eine Übertragung auf andere Elementtypen oder andere Frage-
stellungen leicht möglich.
5.1 Allgemeine Vorgehensweise
Wie einleitend schon herausgestellt, muss man heute die FEM-Anwendung als integralen
Bestandteil einer CAE-Konzeption begreifen. Tatsächlich liegt ein Stück Wirtschaftlichkeit
von CAD und FEM darin, wenn CAD-Modelle von Pre-Prozessoren übernommen, mithilfe
eines FE-Rechenlaufs verifiziert und die Ergebnisse von Post-Prozessoren schnell ausge-
wertet und dargestellt werden können sowie die geänderte Geometrie wieder nach CAD zu-
rückgeführt werden kann.
Ideale Verhältnisse liegen vor, wenn das komplette CAD-Bauteil in verschiedene Layer auf-
gebaut worden ist. Für die FE-Berechnung benötigt man nämlich nur die reine Geometrie,
sodass die Layer, die Vermaßung oder Text enthalten, ausgeblendet werden können. Des
Weiteren kann es sein, dass Bauteile gewisse konstruktive Gegebenheiten enthalten, die für
das Festigkeitsverhalten von geringer Bedeutung sind, aber die Netzgenerierung erschweren
würde. Demgemäß ist zu prüfen, ob geometrische Details vernachlässigt werden können, ob
sich vielleicht Einbau- oder Anbauteile ausklammern lassen oder inwiefern tatsächlich Kon-
takt /STE 92/ zu berücksichtigen ist.
Je nach Bauteilgeometrie und Belastung kann auch ein rekonstruiertes Flächen- oder
Volumenmodell ausreichend sein. Ist ein komplexes räumliches Objekt zu analysieren, ist in
der Regel ein 3-D-Volumenmodell erforderlich.
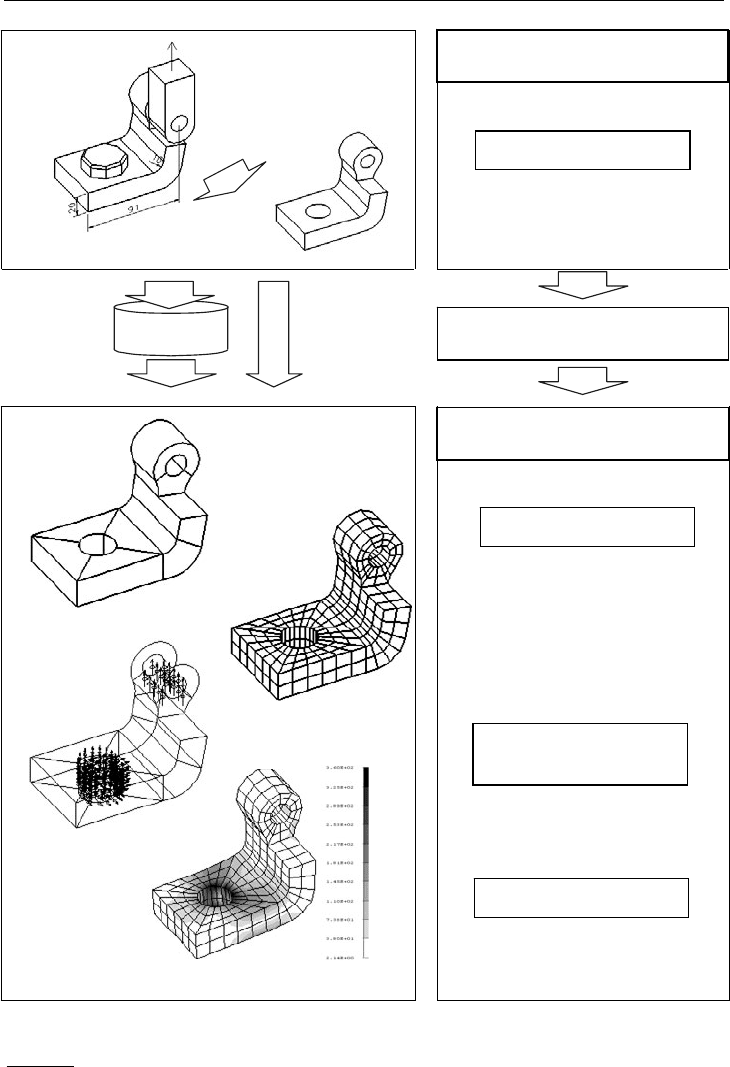
Im Bild 5.1 ist der prinzipielle Ablauf einer integrativen CAE-Kette dargestellt.
x Aufgabe von CAD-Systemen ist es, vollständige Fertigungs- und Montageunterlagen zu
erzeugen. In der Praxis werden dazu Einzelteil-, Gruppen- und Zusammenbau-Zeich-
nungen angefertigt. Aus der Zusammenbau-Zeichnung sind in der Regel die Funktion und
die Belastung zu erkennen.
x Für die Bewährung einer Struktur kann es dabei wichtig sein, einen Gesamtverbund oder
die gefährdeten Einzelteile sicher auszulegen. Im vorliegenden Fall sei unterstellt, dass
die Festigkeit des Hebels für einen Mechanismus entscheidend ist und dieser daher
mittels FEM analysiert werden soll.

5 Das Konzept der Finite-Element-Methode
42
x Aus der entsprechenden Struktur ist daher die Hauptgeometrie herauszulösen, die Rand-
bedingungen festzulegen und die Einleitung der Kräfte zu bestimmen.
x Die nackte Geometrie muss dann an das FE-System übergeben werden. Im Regelfall wird
es dabei so sein, dass ein Schnittstellenprotokoll als IGES-, VDA-FS- oder STEP-File
erzeugt werden muss. Dieses Protokoll kann gewöhnlich verlustfrei übertragen werden.
Neuerdings wird zwischen einigen CAD- und FEM-Systemen auch eine Direktkopplung
(z. B. zwischen CATIA und I-DEAS) realisiert. Die Vollständigkeit der Übertragung wird
hierbei garantiert und die Wirtschaftlichkeit nimmt zu, weil eben zeitintensive Wand-
lungsschritte entfallen.
x Mithilfe eines Pre-Prozessors gilt es weiter, die Geometrie zu einem FE-Modell aufzube-
reiten.
Der erste Schritt dazu ist die Bildung von Makros (diese werden gewöhnlich durch drei
oder vier Seiten begrenzt), aus denen über die Angabe von abgestimmten Seitenteilern ein
Elementnetz generiert werden kann. Hiermit hängt die Typdefinition der Elemente und
deren Spezifizierung unmittelbar zusammen, da hierauf begründet das Eingabeprotokoll
erstellt wird. Dieses Protokoll muss des Weiteren noch um die Werkstoffkennwerte, die
Randbedingungen und die Kräfte vervollständigt werden.
x Mit dem Eingangsprotokoll liegen alle Informationen für den FE-Löser vor. Dieser baut
sich entsprechend der Netztopologie und der Elementkennzeichnung die Steifigkeit der
Struktur auf, arbeitet die Randbedingungen und die Kräfte ein und löst das damit ent-
stehende Gleichungssystem nach den Verschiebungen auf:
(Steifigkeit) x (Verschiebungen) = (äußere Kräfte).
x Aus den Verschiebungen können dann in einer Rückrechnung die auftretenden Deh-
nungen, Spannungen und die Reaktionskräfte ermittelt werden.
x Für eine rationelle Auswertung nutzt man heute leistungsfähige Post-Prozessoren, die die
angefallenen Daten qualitativ und quantitativ auswerten. Derartige Prozessoren können
meist die verformte mit der unverformten Struktur zu einem Verformungsbild überlagern,
die Dehnungen oder Spannungen als Isolinienplot oder Farbfüllbilder gemäß einer Werte-
skala auswerten sowie die Größe und Richtung der Reaktionskräfte darstellen.
Wie ersichtlich, hat dieser Ablauf zwar einige schematische Anteile, hieraus ist aber nicht zu
schließen, dass eine Problembearbeitung mit FEM einem festen Automatismus gehorcht. So
verschiedenartig wie Problemstellungen sein werden, werden auch Lösungsansätze zu ent-
wickeln sein. Das Treffen der Realität hat dabei viel mit der Beherrschung der theoretischen
Möglichkeiten und der Ausschöpfung der Fähigkeiten der Programme zu tun.
In der Praxis ist zunehmend ein Zusammenwachsen von CAD und FEM (z. B. CATIA-V5
mit dem ELFINI-Modul) zu beobachten. Dies bedingt eines CAE-Spezialisten, der von
seinem Ausbildungshintergrund rechnerunterstützte Methoden sicher beherrscht.
5.1 Allgemeine Vorgehensweise
43
3-D-Volumenmodell einer Baugruppe
Herauslösung der Hauptgeometrie
Modellübergabe
Modellübernahme
Konstruktion der Makros
Auswahl des Elementtyps
Festlegung der Elementteiler
Zuführung der Elementdaten
Werkstoffkennwerte
Einführung der Randbedingungen
Einleitung der Kräfte
Berechnung der Verschiebungen
Berechnung der Spannungen
Rückrechnung zu den Reaktionskräften
Darstellung der verformten Struktur
Darstellung der Spannungsverteilung
(Isolinien, Farbfüllbilder)
Bild 5.1: Rechnerunterstützte Bauteilanalyse im interaktiven Dialog
CAD-
Bauteil
vereinfachtes
Analysemodell
CAD-System
Problemaufbereitung
FEM-System
Pre-Prozessing
Lösung des
Gleichungssystems
Post-Prozessing
IGES/
VDA-FS-/
STEP-File
Direkt-
kopplung
Schnittstelle

5 Das Konzept der Finite-Element-Methode
44
5.2 FE-Programmsystem
Die FE-Programme, die sich heute am Markt durchgesetzt haben, sind weitgehend voll-
ständige und durchgängige Systeme.
Mit vollständig soll dabei umschrieben werden, dass man es mit Komplettsystemen zu tun
hat, die unter einer abgestimmten Oberfläche einen Pre- und Post-Prozessor, den
Gleichungslöser sowie verschiedene Ergänzungsmodule verfügbar haben.
Durchgängig kann zudem auch sehr weit reichend sein. Es umfasst die Abbildung von
Geometrie- und Materiallinearität oder -nichtlinearität, Elastodynamik, Thermoelastizität so-
wie sehr schnelle Umformprozesse.
interaktiver
Pre-Prozessor
interaktiver
Post-Prozessor
Elastostatik
Elastodynamik,
implizite
Materialnicht-
linearität
(Plastizität,
Kriechen)
Instabilität
(Knicken, Kip-
pen, Beulen)
Temperatur-
feldanalyse
(stationär,
instationär)
Fluid-
strömungen
(kompressibel,
inkompres-
sibel)
Akustik
Spritzgieß-
simulation
FEM-Universal-
programm
linearer
Programmteil
nichtlinearer
Programmteil
Spezial-
anwendungen
große
Verformungen
Elastodynamik,
explizite
(Crash)
Bild 5.2: Programmstruktur eines kommerziellen FE-Programmsystems
Ein typischer Methodenbaum eines FE-Programms ist im Bild 5.2
gezeigt. Der Grundum-
fang besteht gewöhnlich aus einem linearen Programmteil zur Lösung von elastostatischen
und elastodynamischen Problemen. Hieran können verschiedene Spezialanwendungen ange-

5.3 Mathematische Formulierung
45
koppelt werden, die eigene Routinen darstellen. Insgesamt besteht bei allen Softwarehäusern
das Bestreben, das FEM-Einsatzfeld zu erweitern. Eine sehr wesentliche Erweiterung stellt
die Nichtlinearität dar, und zwar in den Ausprägungen Materialnichtlinearität, geometrische
Nichtlinearität und nichtlineare Strukturdynamik. Hierbei geht es um die realistische Erfas-
sung des Werkstoffverhaltens (Fließen), großer Verformungen (Instabilität) und die Integra-
tion im Zeitbereich (Crash).
Darüber hinaus eignen sich noch die Potenzialprobleme (Wärmeleitung, Magnetfelder, elek-
trische Felder) sehr gut für die numerische Bearbeitung. Somit kann mittlerweile eine große
Klasse von Aufgaben der Technik bzw. der technischen Physik mit der FEM abgedeckt wer-
den.
5.3 Mathematische Formulierung
Die exemplarische Anwendung der im Kapitel 3.4 dargelegten Beziehungen zur Definition
des Steifigkeits-Verschiebungs-Kraft-Zusammenhanges soll im Weiteren an einem eindi-
mensionalen Stab-Balken-Element, und zwar für verschiedene Knotenfreiheitsgrade gezeigt
werden. Dies ist insofern sinnvoll, da mit diesen Einzelfreiheitsgraden später unterschied-
liche Elementtypen aufgebaut werden können. Das Einsatzfeld für Stab-Balken-Elemente ist
die Fachwerkanalyse oder im Maschinenbau die Analyse von Wellen hinsichtlich Durchbie-
gung und Eigenfrequenzen.
5.3.1 Ebenes Stab-Element
Das finite Stab-Element ist zuvor schon im Kapitel 4 als diskretes Federelement eingeführt
worden. Innerhalb der FEM wird es jedoch als Kontinuumselement mit den beschreibenden
Eigenschaften Geometrie und Werkstoff benutzt. Um den Zusammenhang zwischen den
Verformungen, der Geometrie und dem Werkstoff herstellen zu können, muss die ent-
sprechende Differenzialgleichung aufgestellt werden.
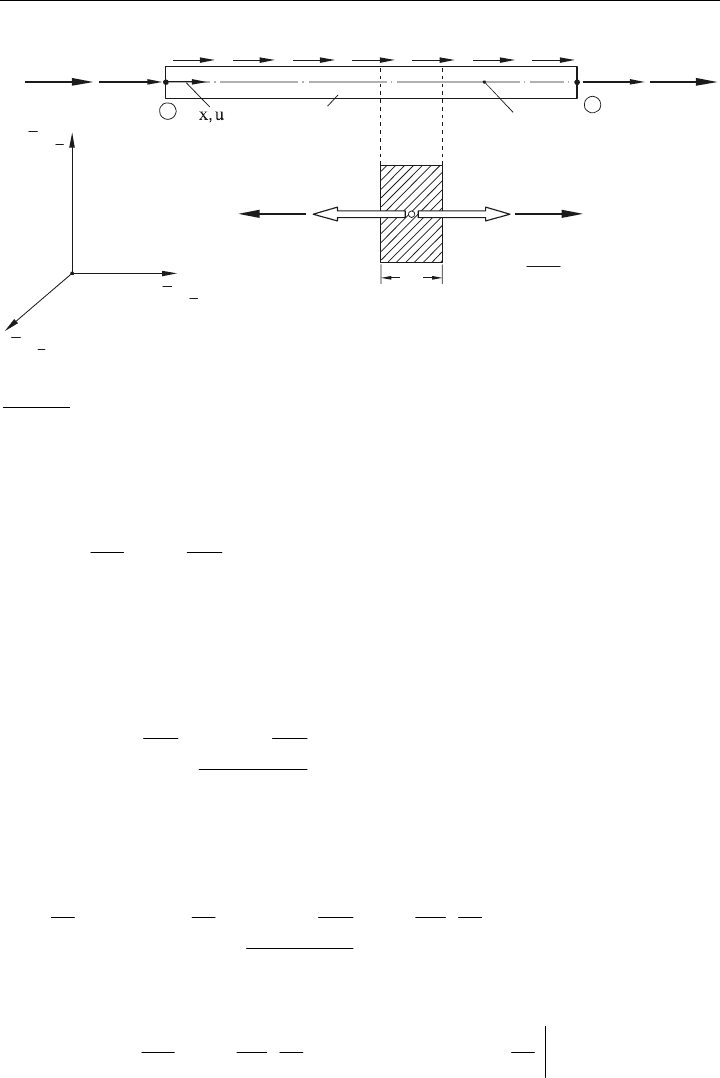
Als verallgemeinerter Fall ist demgemäß von einem longitudinal schwingenden Element
auszugehen. Im nachfolgenden Bild 5.3 ist dies beispielhaft charakterisiert. Merkmal ist
hierbei, dass alle Kraftgrößen (Knotenkräfte und verteilte Kräfte) nur in Längsrichtung
auftreten und hierzu auch Knotenreaktionen
u
i
(i = 1, 2) korrespondieren. Je Knoten tritt
also ein axialer Freiheitsgrad auf. Für die Beschreibung des Elements sind weiterhin noch
erforderlich: Dichte U , Elastizitätsmodul E, Querschnittsfläche A und Länge L.
Die Eigenschaften des Elements werden in einem lokalen Koordinatensystem beschrieben.
Später ist das Element in einer Struktur in beliebiger Lage zu einem globalen Koordinaten-
system eingebaut. Gemäß der Lage und der Belastung der Struktur ändert sich dann insbe-
sondere die Steifigkeit des Elements, wodurch ein anderer Verschiebungszustand induziert
wird. Dementsprechend ist eine transformierte Steifigkeitsmatrix zu erstellen, so wie dies
später im Kapitel 5.4.1 gezeigt wird.
5 Das Konzept der Finite-Element-Methode
46
(lokales KS)
N
2
N
1
1
2
(globales KS)
A
x
V
dxp
x
üdxA
U
LAE
,,
U
dx
Adx
x
x
x
¸
¹
·
¨
©
§
w
V
w
V
u(x,
t)
),x(p
x
t
x
F,x
z
F,z
y
F,y
22
u,u
11
u,u
Bild 5.3: Mechanik des linearen Stab-Elements
Stellt man nun an einem infinitesimalen Stab-Elementchen mit der Länge dx das Gleichge-
wicht her, so folgt daraus die DGL:
0p
x
u
AE
u
Aȡ
x
2
2
2
2
w
w
w
w
t
. (5.1)
Durch Heranziehung des Galerkin‘schen Formalismus (s. Gl. (3.41)) gilt es weiter, die finite
Gleichung zu erstellen. Dazu multiplizieren wir die DGL mit einer noch unbekannten Form-
funktion g x
j
, die später erst elementspezifisch definiert wird und bilden das Funktional
³
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
U
L
o
xj
2
2
j
2
2
j
0dxpg
x
u
gAE
u
gA
t
, j = 1, 2. (5.2)
Als Endergebnis soll die einfache Schwingungsdifferenzialgleichung vorliegen, weshalb wir
den mittleren Term mit der Produktregel der Differenziation um eine Ordnung erniedrigen
müssen, hiernach gilt:
x
u
x
g
AE
x
u
gAE
x
u
xgAE
x
j
2
2
jj
w
w
w
w
w
w
¸
¹
·
¨
©
§
w
w
w
w
.
Wird dies berücksichtigt, so kann die vorstehende Gleichung auch geschrieben werden als
0
o
L
x
u
gAEdxpg
x
u
x
g
AE
u
gA
j
L
o
xj
j
2
2
j
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
U
³
t
(5.3)
und mit ausintegrierten Randtermen bzw. an den Integrationsgrenzen
5.3 Mathematische Formulierung
47
³
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
U
L
o
0jLjxj
j
2
2
j
0
x
u
0gAE
x
u
LgAEdxpg
x
u
x
g
AE
u
gA
t
.
An dieser Stelle wollen wir nun mit
tt,
i
2
1i
i
uxgxu
¦
(5.4)
einen Ansatz
*)
für die unbekannten Verschiebungen einführen, und zwar so, dass von den
Knotenverschiebungen
u
i
ausgehend in das Innere des Elements u (x, t) hineinapproximiert
werden kann. Die dazu erforderlichen Formfunktionen
gg
ij
,
wählen wir linear unabhängig,
und zwar so, dass alle Randbedingungen erfüllt werden. Weiterhin soll noch in eine Orts-
und Zeitabhängigkeit separiert werden. Damit folgt dann mit den notwendigen Ableitungen
i
2
1i
i
2
i
2
2
1i
i
2
2
u
x
g
x
u
,
u
g
u
¦¦
w
w
w
w
w
w
w
w
tt
für die Gl. (5.3)
.2,1j,0u
x
xg
0gAEu
x
xg
LgAE
dxpgdxu
x
g
x
g
AE
u
ggAȡ
0
2
1i
i
i
jL
2
1i
i
i
j
L
o
xj
2
1i
L
o
i
i
j
2
i
2
ij
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
w
w
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
¦¦
³
¦
³
t
(5.5)
Löst man diese Gleichung auf, so ergibt sich
,2,1j0gNLgN
dxpgudx
x
g
x
g
AE
u
dxggAȡ
j1j2
L
o
xj
2
1i
i
i
L
o
j
L
o
2
i
2
ij
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
w
w
w
w
w
w
³
¦
³³
t
(5.6)
wobei jetzt Massen, Steifigkeiten, Knotengrößen und Kräfte abgespalten sind. Somit ist die
gesuchte Schwingungsdifferenzialgleichung
K0
ppukum
(5.7)
in diskretisierter Form zu erkennen. Ausgeschrieben lautet diese Matrizengleichung auch
*)
Anmerkung: Rayleigh-Ritz-Ansatz = Linearkombination von orts- und zeitabhängigen Form- bzw. Ansatz-
funktionen
