Кулагин В.А., Грищенко Е.П. Гидрогазодинамика

Подождите немного. Документ загружается.

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ

4.1. Понятие поля физической величины



Гидрогазодинамика. Учеб. пособие 61

абс



обр



ний тока образует трубчатую поверхность – трубку тока, или векторную

трубку (рис. 4.4

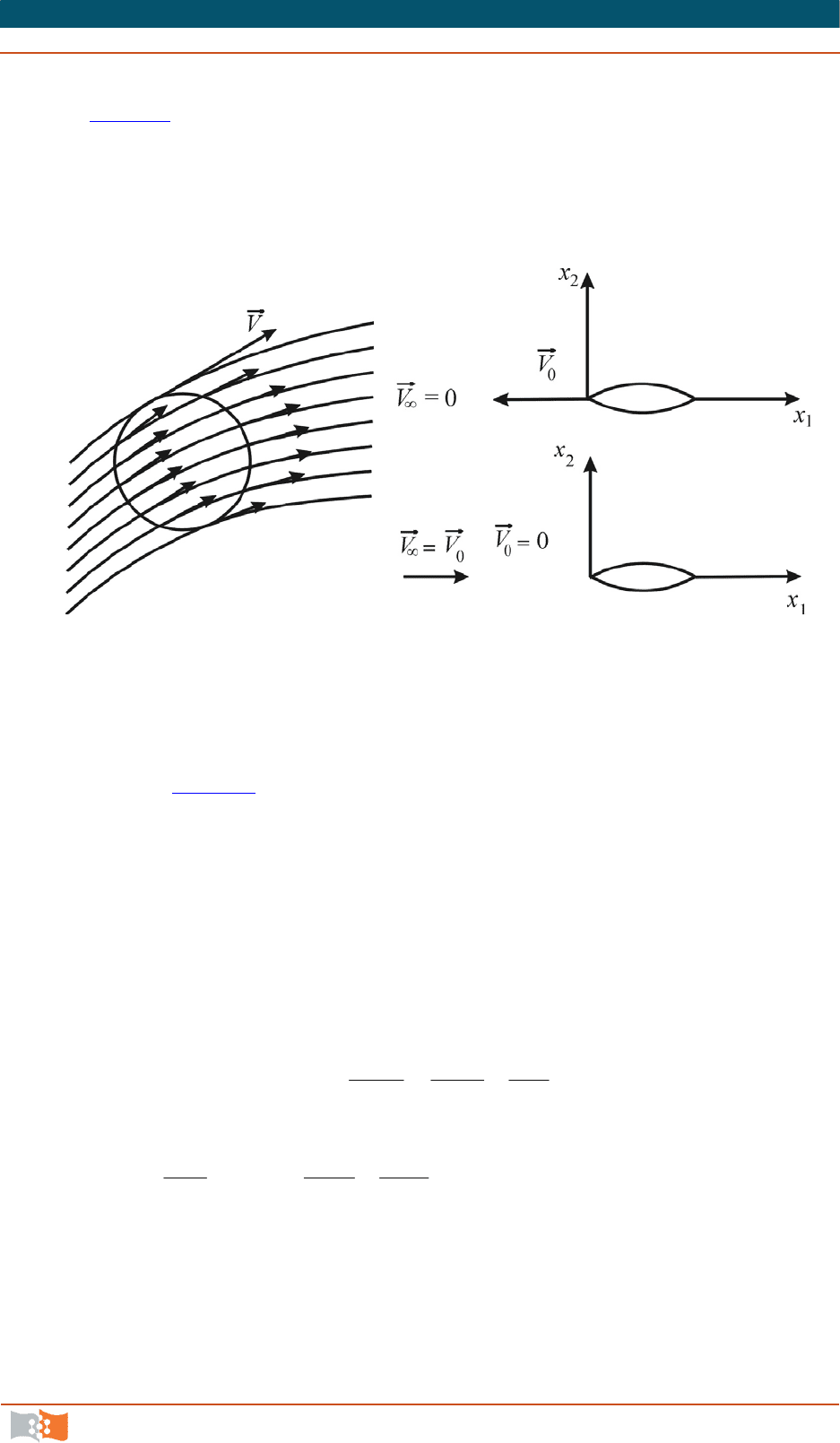
В опытах по изучению движения тел в жидкости часто используют от-

носительное (обращенное) движение, когда тело и связанная с ним система

координат неподвижны. Набегающему потоку сообщают постоянные скоро-

сти, равные по величине и противоположные по направлению скорости тела.

Рис. 4.4 Рис. 4.5

К установкам, в которых используется принцип обращенного движе-

ния, относятся аэро- и гидродинамические трубы и гидролотки.

В кинематическом отношении движения абсолютное и обращенное не

совпадают (см. рис. 4.5

, где показаны скорости вблизи тела и далеко на бес-

конечности от него). Силы же, действующие в жидкости, одинаковы в обоих

случаях. Поскольку связь между скоростью абсолютного и

обращенного движения можно представить в виде

0абсобр

VVV





для ускорений соответственно

0абс

обр





Так как





, то

абс

обр





, что и доказывает предположение о

равенстве сил в обоих случаях.

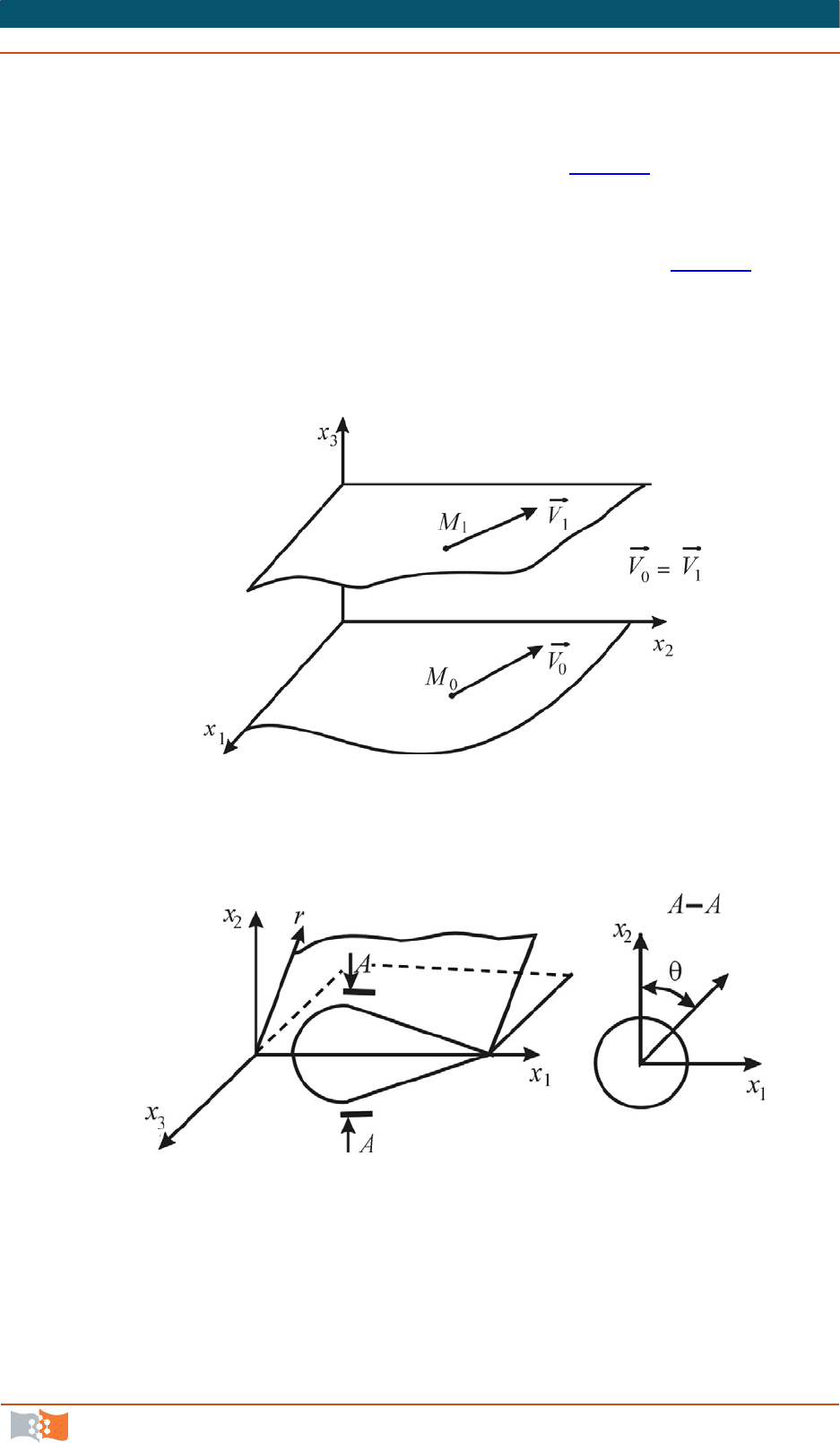
Течения жидкости могут быть также пространственными, плоскопа-

раллельными и осесимметричными. Поле скоростей соответственно можно

представить в следующем виде:

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ

4.1. Понятие поля физической величины



Гидрогазодинамика. Учеб. пособие 62





3213,2,1

,, xxxfV 

для пространственного течения;



212,1

xxfV 

V

для плоскопараллельного течения, когда картина

течения в плоскостях, нормальных к некоторой оси (рис. 4.6

), одинакова;



trxfV



V

в случае осесимметричного течения в цилиндри-

ческой системе координат, когда поле скоростей во всех плоскостях, прохо-

дящих через некоторую прямую (ось симметрии), одинаково (рис. 4.7

В декартовой системе координат поле скоростей для осесимметричного

случая определяется уже тремя пространственными координатами. Наи-

большую сложность для изучения представляют пространственные течения

как общий случай движения жидкой среды.

Рис. 4.6

Рис. 4.7

Трубка тока и струя  это не одно и то же. Струя образована траекто-

риями частиц движущейся жидкости. Трубка тока – совокупность линий то-

ка.

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ

4.1. Понятие поля физической величины



Гидрогазодинамика. Учеб. пособие 63

Ниже приведены примеры определения линий тока и траекторий по за-

данному полю скоростей.

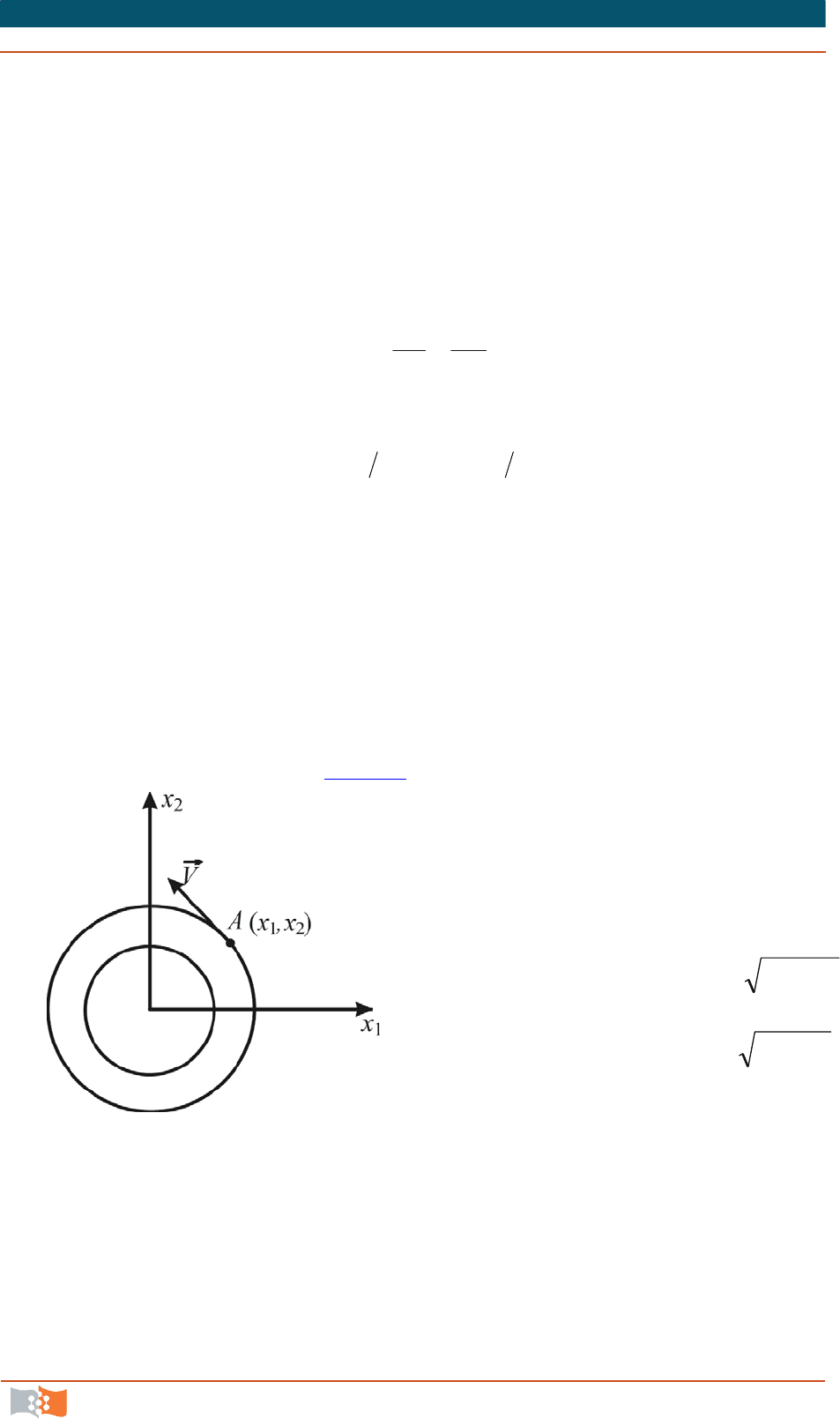
Пример. Движение жидкости задано проекциями скоростей

axV





axV 

V

, где а  постоянная.

Исследуемое движение является плоским (



) и установившимся,

т. к.

от времени не зависят.

Запишем дифференциальные уравнения линий тока:



или, подставляя значения

в последнее выражение,





1221

axdxaxdx





Разделив переменные, получим

2211





dxxdxx

и, интегрируя, найдем уравнение линий тока:

Cxx 

которое представляет собой семейство концентрических окружностей с

центром в начале координат (рис. 4.8

). Такое движение называется плоским

вихрем. Траектории в данном случае

совпадают с линиями тока. Направле-

ние движения жидкости определяется

по косинусам углов между вектором

скорости и началом координат:





1211

// сos xxxVVxV 









1122

// сos xxxVVxV 





Рис. 4.8

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ



Гидрогазодинамика. Учеб. пособие 64

Для глубокого и всестороннего исследования движения жидкости не-

обходимо знать для каждого момента времени и каждой частицы жидкости

ее местоположение в пространстве. В механике жидкости с этой целью ис-

пользуются два метода кинематики  Лагранжа и Эйлера.

По методу Лагранжа изучается поведение отдельной частицы жидко-

сти за время ее движения в пространстве. Пусть в начальный момен

т времени

выделенная жидкая частица характеризуется определенными тремя чис-

лами a, b, c, которые служат обозначением данной частицы жидкости при ис-

следовании течения. Пусть в любой другой момент времени

координатами

частицы в прямоугольной системе координат будут x

, x

. Эти координаты

являются функциями не только времени движения (начиная с

), но и на-

чальных координат – тройки чисел a, b, c, обозначающих частицу, т. е.



















. , , ,

, , , ,

tcbaxx

(4.1)

Уравнения (4.1) и числа a, b, c и

называются соответственно уравне-

ниями и переменными Лагранжа. Уравнениями (4.1

), по сути, задаются тра-

ектории движения отдельных частиц жидкости. Для полной характеристики

состояния движущейся жидкости необходимо знать распределение давления

и плотность



. Уравнения движения, составленные по методу Лагранжа,

обычно трудно разрешимы.

Метод, предложенный Эйлером, проще и нашел более широкое приме-

нение на практике. Этот метод не учитывает индивидуальных траекторий от-

дельных частиц. Здесь достаточно знать скорость жидкости в каждой точке

пространства и ее направление, т. е. знать поле скоростей, которое в общем

случае мо

жет изменяться в пр

остранстве и во времени:



















. , , ,

, , , ,

32133

32122

32111

txxxVV

(4.2)

Совокупность величин x

, x

, t называют переменными Эйлера; дви-

жение среды, по Эйлеру, задается полем скоростей.

Основное различие методов Лагранжа и Эйлера заключается в выборе

системы отсчета: по Лагранжу, система a, b, c связана с жидкостью; по Эйлеру,

, x

 это некоторая система координат, относительно которой протекает

жидкость. Оба метода равноправны.

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ



Гидрогазодинамика. Учеб. пособие 65

Как уже отмечалось, линия тока – это геометрическая линия, проходя-

щая через различные точки пространства в данный момент времени так, что

векторы скоростей находящихся там частиц будут касательными к этой ли-

нии. Линии тока можно непосредственно наблюдать или сфотографировать,

если ввести в поток какой-либо краситель или прикрепить к поверхности об-

текаемого тела (кры

ла и т

. п.) шелковинки.

Траектория частицы – это линия, определяющая положение частицы в

разные моменты времени.

Линия тока отличается от траектории тем, что указывает направление

скоростей разных частиц в один и тот же момент времени. Имеется лишь

один, но весьма важный случай, когда линии тока совпадают с траекториями.

Это случай устано

вившегося движения





const



tVV

. Каждая частица в

этом случае движется по линии тока, т. к. в любой точке на своем пути она

имеет скорость, которую имели все частицы, проходившие через эту точку в

другие моменты времени.

Предположим, что поле

(совокупность точек простран-

ства, занятого потоком) скоро-

стей известно и нужно найти

линию тока. Из определения

линии тока следует, что вектор

скорости направлен к ней по

касат

льной. Выделим на ли-

нии тока (рис. 4.9

) элемент ду-

ги

с проекциями на декар-

товы оси координат dx

, dx

. Так как вектор скорости



и вектор



параллельны, то векторное произведение их равно нулю:

0VSd



. (4.3)

Запишем это равенство с помощью определителя третьего порядка:

321



VVV

dxdxdx

kji

. (4.4)

Рис. 4.9

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ

4.3. Основные кинематические элементы движения жидкости



Гидрогазодинамика. Учеб. пособие 66

Рис. 4.10

Определитель равен нулю, если элементы двух его строк равны или

пропорциональны, отсюда



. (4.5)

Полученная система представляет дифференциальные уравнения

линий тока. Интегрируя ее, находят положение линий тока в данный мо-

мент времени.

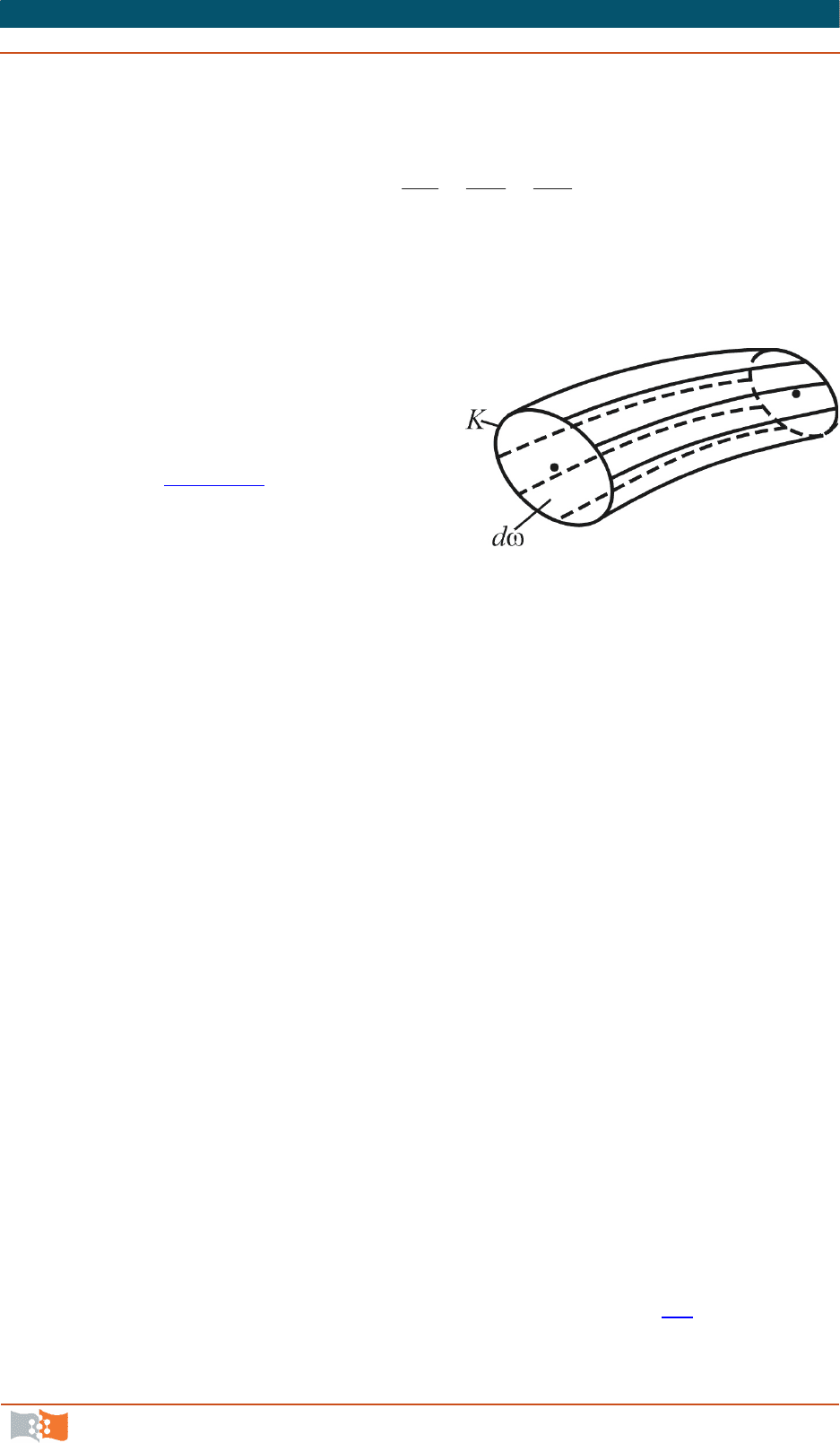
Если в потоке жидкости на-

метить точку и выделить вокруг

нее элементарную площадку



ограниченную пространственным

контуром

(рис. 4.10), то сово-

купность линий тока, проведенных

через все точки элементарной

площадки

d

, образует трубку то-

ка, математический аналог элемен-

тарной струйки.

В случае установившегося движения элементарная струйка обладает

следующими тремя свойствами:

так как линии тока при установившемся движении жидкости с течени-

ем времени не меняют своей формы, то и струйка тока является неизменной

во времени;

так как боковая поверхность струйки образована линиями тока, вдоль

которых одна за другой скользят частицы жидкости, то проникновение жи

д-

кости чер

ез боковую поверхность струйки невозможно. Элементарная струй-

ка как бы заключена в жесткие, не изменяющиеся во времени, водонепрони-

цаемые стенки, не имеющие толщины;

так как площадь поперечного сечения элементарной струйки считается

бесконечно малой, то величину скорости и давления для всех точек данного

поперечного сечен

ия струйки следует

считать одинаковыми.

Так как для точки с положительным значением координат



0 сos







, а



0 сos







, то скорость образует с осью

угол





и,

следовательно, движение происходит против часовой стрелки.

Пример. Движение жидкости задано проекциями скоростей

txV 

txV 





. Найти линии тока и траектории.

Движение плоское (



) и неустановившееся, т. к.

зависят от

координат и времени. Следовательно, траектории и линии тока здесь не сов-

падают.

Интегрируя дифференциальное уравнение линий тока (4.5

)

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ

4.3. Основные кинематические элементы движения жидкости



Гидрогазодинамика. Учеб. пособие 67









txdxtxdx









2211

для фиксированного

, получим









,Ctxtx









т. е. линии тока в каждый момент времени представляют собой семей-

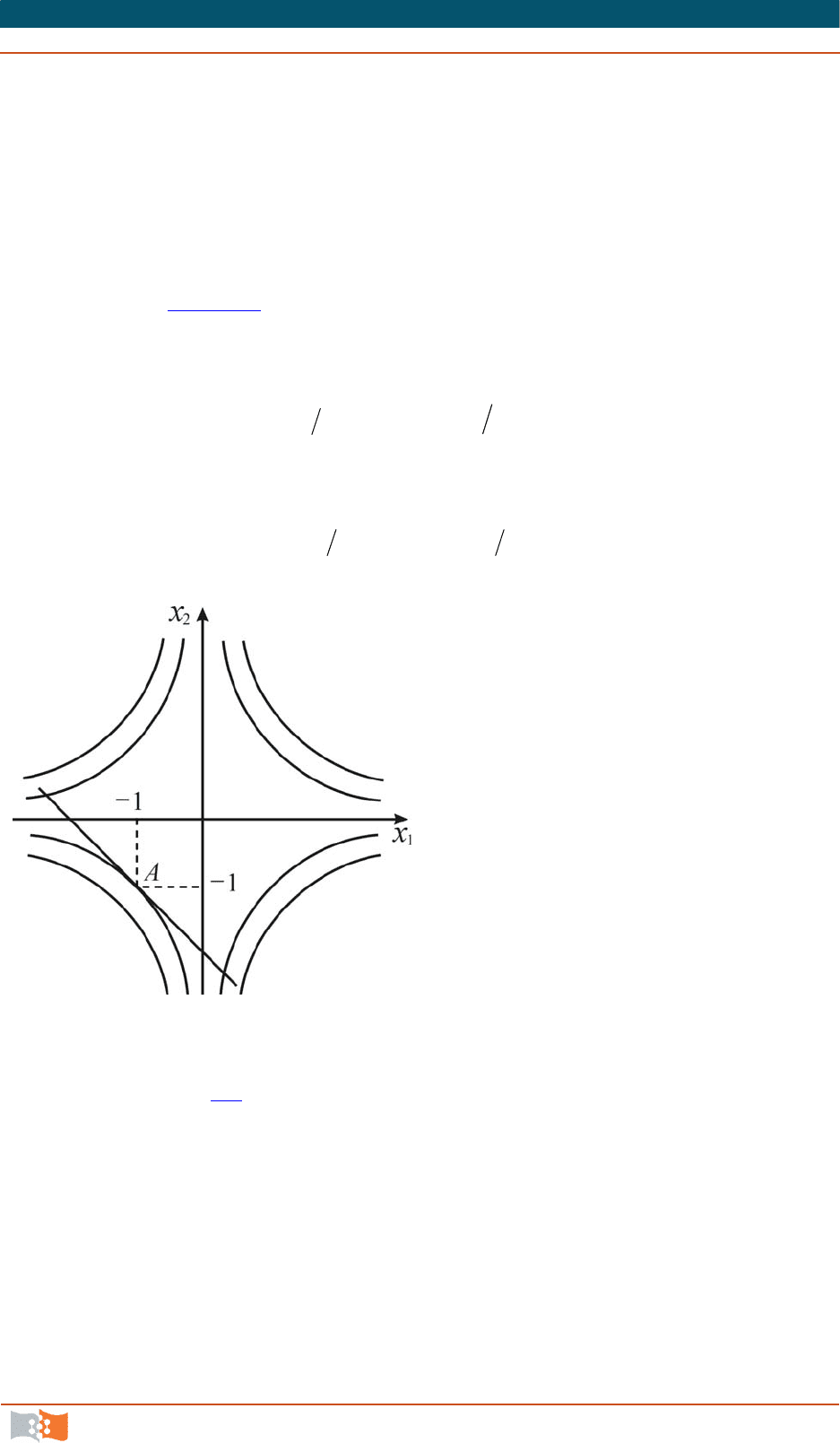
ство гипербол (рис. 4.11

Для определения траекторий необходимо проинтегрировать уравнения

линий тока:

txdtdx





;

txdtdx







или, в явном виде,

txdtdx





;

txdtdx





Каждое из этих уравнений

представляет собой линейное не-

однородное уравнение с постоян-

ными коэффициентами. Решение

их дает, как известно из математи-

ки, следующее выражение:















.teCx

teCx

(4.6)

Траекторию, которую опи-

сывает частица жидкости, нахо-

дящаяся в момент времени в точке

(1, 1), найдем после опреде-

ления постоянных

. Для

этого подставим в (4.6

) значения 0











, получим



СС

Следовательно, для искомой траектории





 tx

или, исключая

время,



 xx

, т. е. траектория частицы А есть прямая линия.

Вихревое движение. Вектор, равный удвоенному вектору угловой

скорости





частицы, называется вихрем и обозначается





2rot V

. Вихрь

характеризует вращение частиц вокруг некоторой оси. Вращательное движе-

ние жидкости с наличием компонентов вихря называется вихревым. Вихре-

вое движение может быть плоским и пространственным.

Рис. 4.11

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ

4.3. Основные кинематические элементы движения жидкости



Гидрогазодинамика. Учеб. пособие 68

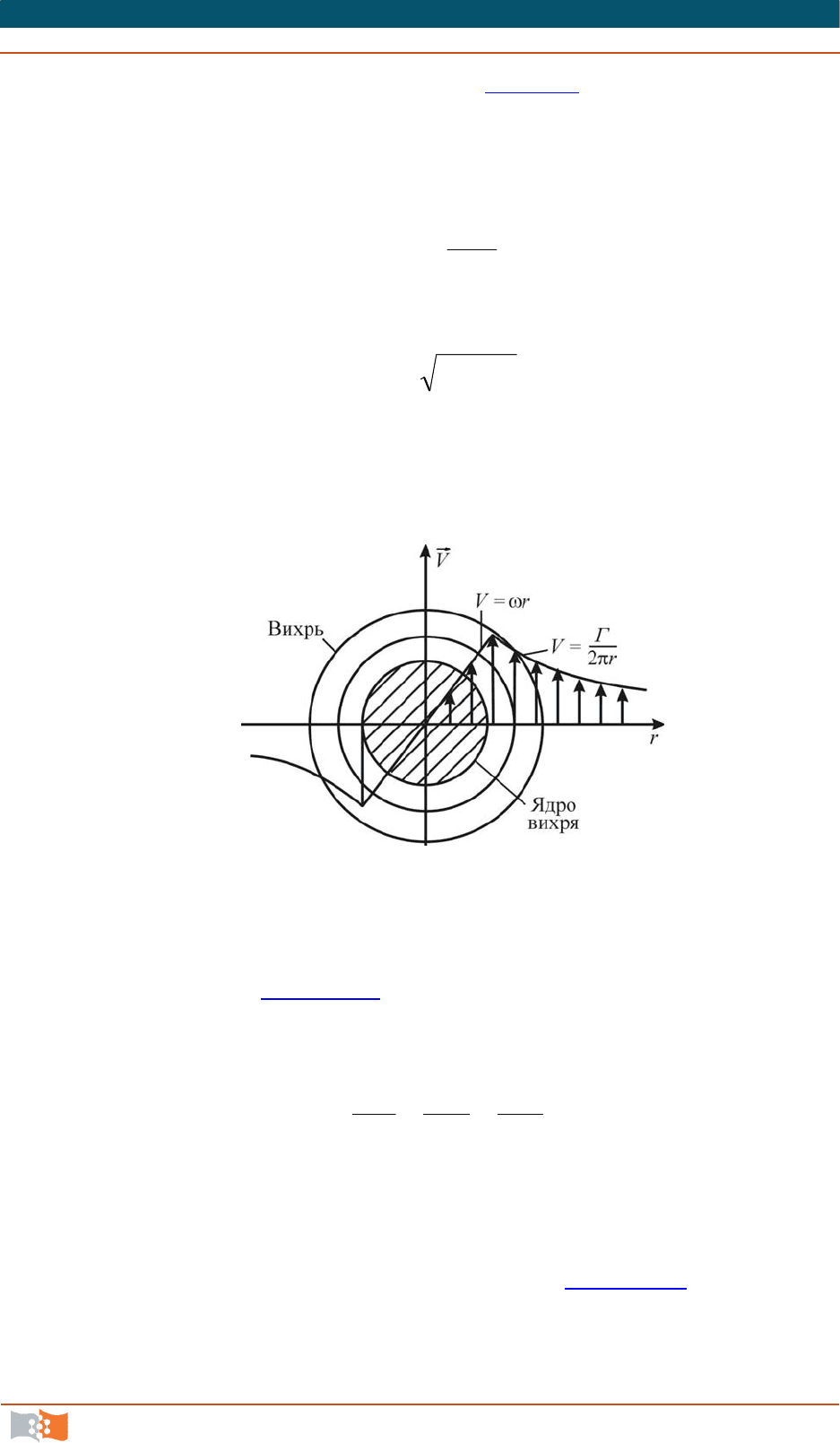
Пример. Рассмотрим плоский вихрь (рис. 4.12), линии тока и траекто-

рии которого представляют собой концентрические окружности с центром в

начале координат.

Можно также показать, что скорости, вызванные плоским вихрем, оп-

ределяются из выражения

2 r









где Г



циркуляция; r



расстояние от центра вихря,

xxr 

Скорость в центре вихря теоретически (r = 0) должна равняться беско-

нечности, что не согласуется с опытами для реальной жидкости. Поэтому дела-

ется допущение, что некоторая область вокруг центра вихря (ядро вихря) вра-

щается как твердое тело, т. е. скорости в ядре пропорциональны радиусу.

Рис. 4.12

Если в данный момент времени можно провести геометрические ли-

нии, касательные к векторам угловых скоростей частиц, то эти линии будут

называться вихревыми (рис. 4.13, а

Дифференциальные уравнения вихревых линий по аналогии с уравне-

ниями линий тока могут быть записаны в виде









 d

где dx

, dx

 проекции элементарного участка вихревой линии в

декартовой системе координат; d

, d

 проекции угловой скорости.

Совокупность вихревых линий, проведенных через точки произвольно-

го замкнутого контура, образует вихревую трубку (рис. 4.13, б

). Объем жид-

кости, заключенный внутри вихревой трубки, называется вихревым шнуром,

например, ядро вихря, все точки которого вращаются с постоянной угловой

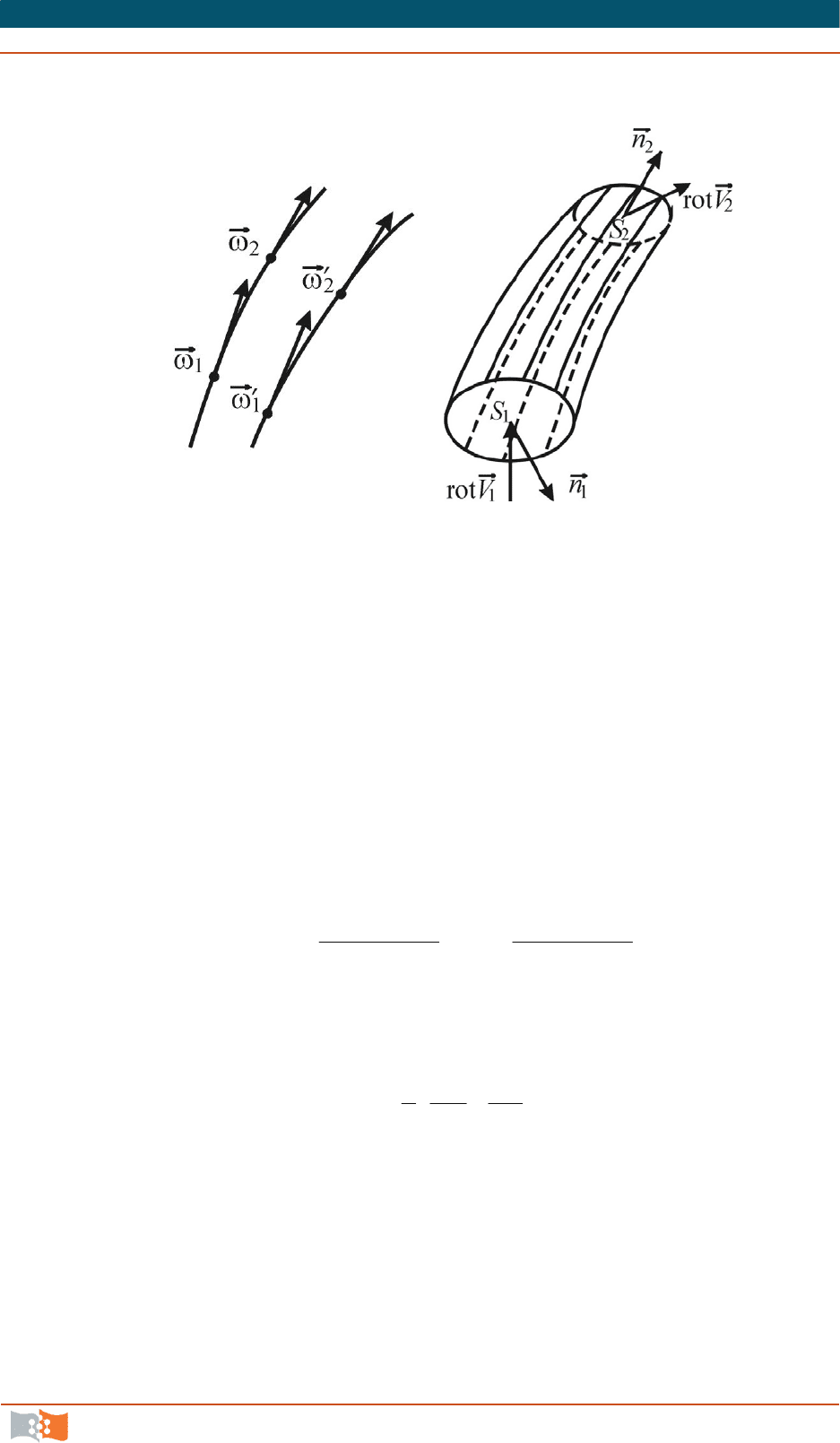
4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ

4.3. Основные кинематические элементы движения жидкости



Гидрогазодинамика. Учеб. пособие 69

а б

Рис. 4.13

скоростью. Остальная часть плоского вихря, находящаяся вне ядра,

движется по круговым траекториям без поворота (вращения) частиц. Это

можно показать на примере.

Пример. Определить угловые скорости вращения частиц в поле плос-

кого вихря.

Проекции вектора угловой скорости вращения вокруг осей х

и х

рав-

ны нулю, т. к.

V

, а

не зависят от координаты

. Подставив зна-

чения



2 xx







;



2 xx







в формулу





















получим  = 0. Таким образом, понятия «вихрь» и «вращение частиц»

неоднозначны и смешивать их нельзя.

В первом случае частицы движутся поступательно по траекториям –

концентрическим окружностям, а во втором – вращаются относительно соот-

ветствующей (мгновенной) оси.

4. КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ

4.3. Основные кинематические элементы движения жидкости



Гидрогазодинамика. Учеб. пособие 70

Следовательно, при круговом движении может не быть вращения час-

тиц и, наоборот, оно может иметь место при прямолинейном движении.

Влияние вихревой трубки на жидкость характеризуется ее интенсивно-

стью, т. е. потоком вектора вихря



rot

через поперечное сечение вихревой

трубки. Интенсивность

определяется по выражению





dSnVi



rot

где



 нормаль к поперечному сечению

трубки.

В случае если вихри непрерывно распределены по поверхности, они об-

разуют вихревой слой. Идеализированный вихревой слой (толщина его стре-

мится к нулю при неизменной интенсивности) называется вихревой пеленой.

Вихрь скорости, а также угло-

вую скорость и интенсивность вихре-

вой трубки измерить непосредственно

нельзя. Наглядно представить интен-

сивность можно, используя такое

фундамен

тальное поня

тие, как цирку-

ляция скорости.

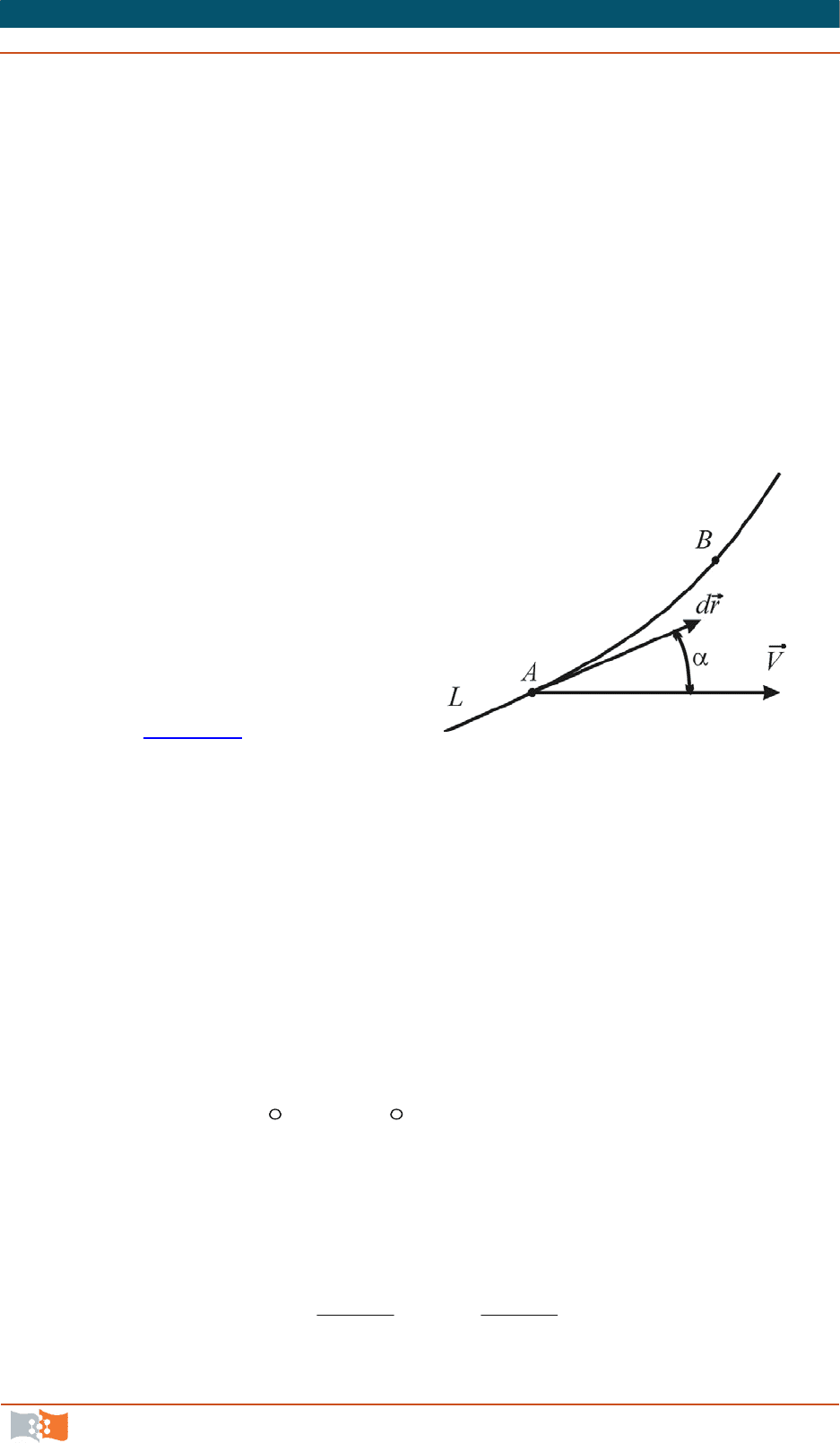
Циркуляция скорости представ-

ляет собой криволинейный интеграл

по контуру (рис. 4.14

) от скалярного

произведения вектора скорости



на

дифференциал направленного отрезка

дуги контура







rdV





Раскрыв скалярное произведение, получим







dxVdxVdxV

332211



. Для замкнутого контура циркуляции вектора

скорости определяются контурным интегралом









dxVdxVdxVrdV

332211



Пример. Вычислить циркуляцию скорости по контуру, соединяющему

точки с координатами А(х

, 0) и В(0, х

) в потоке жидкости, который задан

проекциями скорости









V

Рис. 4.14