Кулагин В.А., Грищенко Е.П. Гидрогазодинамика

2. ЭЛЕМЕНТЫ ТЕНЗОРНОГО АНАЛИЗА

2.3. Тензорная алгебра



Гидрогазодинамика. Учеб. пособие 31

7. Векторно-векторное произведение трех векторов (дает вектор)













baccabcba





. (2.41)

Доказательство несколько громоздко, но элементарно. Оно приведено

во всех учебниках по высшей математике.

8. Произведение тензора 2-го ранга на вектор (дает вектор):

суммирование по j от 1 до 3:





jij

i

aΤaΤ







; (2.42)

суммирование по

j

от 1 до 3:







i

*

j

*

ijjij

i

aΤaΤΤaΤa





. (2.43)

Такие произведения дают действительно вектор, что проверяется вы-

кладкой



,aΤαααaαΤααaΤaΤ

SkrjSjrikSjSkrjrikjij

i



















k

ikSkrikSkrjSjrik

aΤαaΤαaΤααα





,

т. е. произведение равно 1 при

S

r



и 0 при

S

r



.

9. Тензорное (внутреннее точечное) произведение двух тензоров 2-го

ранга (дает тензор 2-го ранга, называемый сверткой исходных тензоров)





kjik

ij

QPQP





. (2.44)

Например,



32332232123123

32

QPQPQPQPQP

kk







.

10. Скалярное (внутреннее, двухточечное) произведение двух тензо-

ров 2-го ранга (дает скаляр, называемый двойной сверткой, шнуром или сле-

дом исходных тензоров)









PQPQQPQP

ijijijij

::





(2.45)

(здесь двойные суммирования по i и по j от 1 до 3).

2. ЭЛЕМЕНТЫ ТЕНЗОРНОГО АНАЛИЗА



Гидрогазодинамика. Учеб. пособие 32

2

.

4

.

К

р

и

в

о

л

и

н

е

й

н

ы

е

к

о

р

д

и

н

а

т

ы

.

К

о

э

ф

и

ц

и

е

н

т

ы

Л

я

м

е

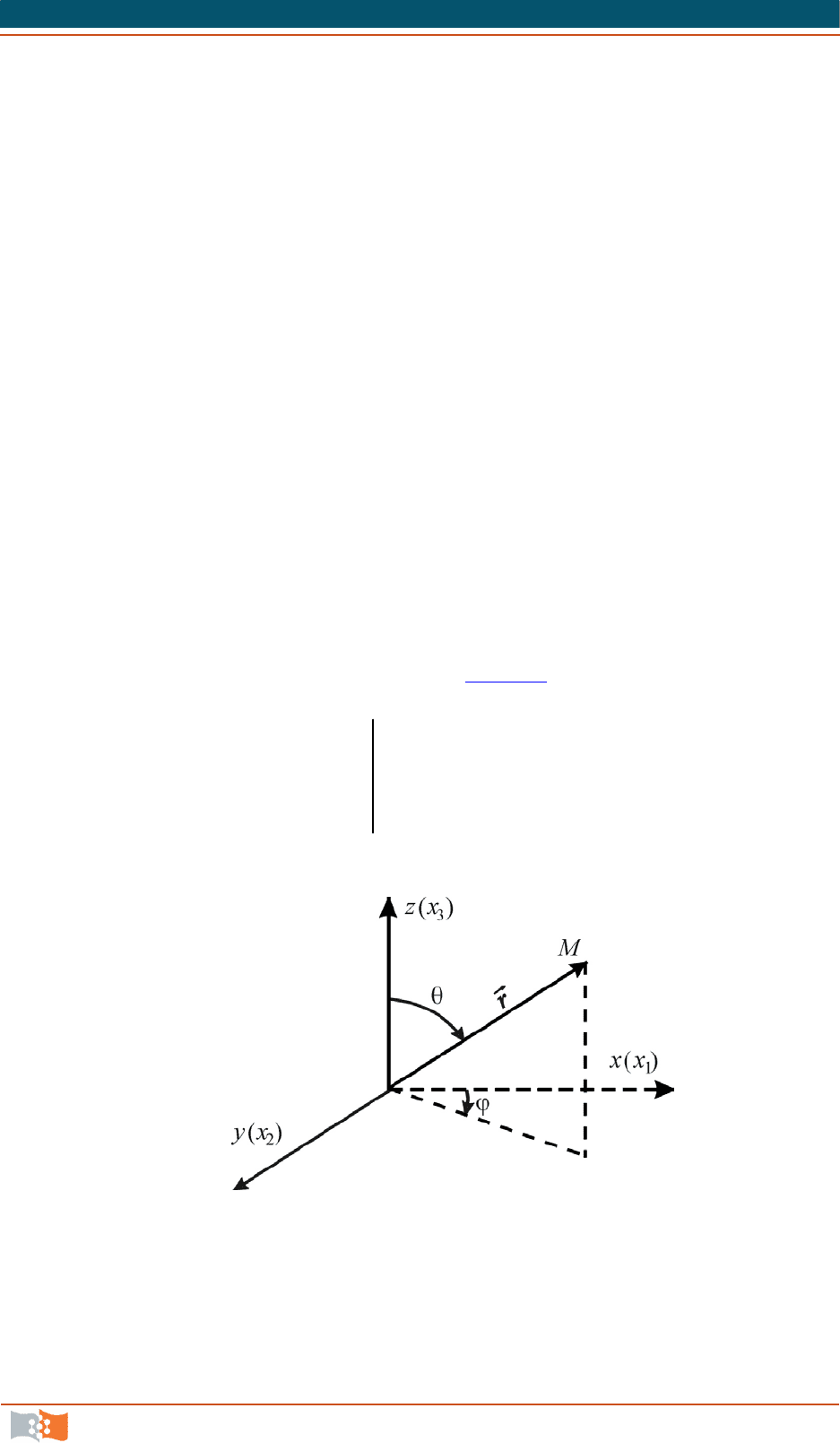
Положение точки M в пространстве E

3

однозначно находят радиусом-

вектором

r



или тройкой независимых между собой величин q

1

, q

2

, q

3

, назы-

ваемых обобщенными координатами. Условие q

1

= const определяет неко-

торую координатную поверхность Q.

Линия пересечения поверхностей Q

1

и Q

2

(линии с q

3

= Var)









const.

const,

2

1

q

(2.46)

Точка М пересечения трех координатных поверхностей Q

1

, Q

2

, Q

3













const.

const,

3

2

1

q

(2.47)

Пример. Сферические координаты (рис. 2.3

):

11

22

33

02const-плоскость ,

0 const конус ,

0constсфера .

qQ

qrRr Q





 





  





  



(2.47а)

Рис. 2.3

Таким образом,

2. ЭЛЕМЕНТЫ ТЕНЗОРНОГО АНАЛИЗА

2.4. Криволинейные координаты. Коэффициенты Ляме



Гидрогазодинамика. Учеб. пособие 33





k

qrqqqrxixixizkyjxir









321332211

,,

. (2.48)

Изменив лишь одну из обобщенных координат (две другие неизмен-

ны), получим частную производную









.

,,,,

lim

0

k

jikjikk

q

k

q

qqqrqqqqr

q

r

k

















(2.49)

Поделив значение этой производной на ее модуль

k

q

r





, получим еди-

ничный вектор opm e

k

для координатной линии q

k

:

,

k

q

r

q

r

e

k







(2.50)

где

k

q

r







 коэффициент Ляме.

Итак,

kkkk

dqerd









. (2.51)

Пример. Вычисление ортов цилиндрической системы координат через

орты декартовой системы (рис. 2.4

).

,

332211

xixixir





, ,sin ;cos

3321

xxxx















.

1

coscos

21

2

3

2

1

3

2

1























































































ii

x

xx

x

i

x

i

x

i

r

e





2. ЭЛЕМЕНТЫ ТЕНЗОРНОГО АНАЛИЗА

2.4. Криволинейные координаты. Коэффициенты Ляме



Гидрогазодинамика. Учеб. пособие 34

Рис. 2.4

Аналогично найдем

321

3

;cossin ieiie

x







. Коэффициенты Ляме

при этом будут иметь значения

1 ; ;1

3















 x

. С учетом, что для сфери-

ческой системы координат







sinr

и

,cos





Rz

имеем для этой системы ко-

ординат





















. ;sinsincoscoscos

,sin ;cossinsinsin

,1 ;coscossincossin

321

21

2321

riiie

riie

iiie

r









(2.52)

Запишем условие ортогональности ортов:

0





ki

qq

ee



. (2.53)

Условие некомпланарности





,0

321







eee



(2.54)

т. е. эти векторы не лежат в одной плоскости.

Различают координаты прямоугольные (прямолинейные и криволи-

нейные) и криволинейные (прямоугольные и косоугольные). Наиболее рас-

пространены прямоугольные системы координат. Декартовые представляют

собой прямоугольные прямолинейные координаты. Сферические и цилинд-

рические – прямоугольные криволинейные координаты. Выбирают и вводят

соответствующие системы координат для удобства формулирования законов

МЖГ и решения конкретных

задач. Например, для расчета расширения сфе-

ры удобна сферическая система координат, в которой все характеристики тече-

ния будут зависеть лишь от координаты

r (и, может быть, еще от времени).

2. ЭЛЕМЕНТЫ ТЕНЗОРНОГО АНАЛИЗА



Гидрогазодинамика. Учеб. пособие 35

2

.

5

.

П

р

е

о

б

р

а

з

о

в

а

н

и

е

О

с

т

р

о

г

р

а

д

с

к

о

г

о

–

Г

а

у

с

а

.

О

п

е

р

а

т

о

р

Г

а

м

и

л

ь

т

о

н

а

Напомним некоторые определения и формулы математического анали-

за: производная непрерывной функции



;lim

0

x













(2.55)

формула Ньютона

 Лейбница для определения интеграла от непре-

рывной функции

  

;







b

a

abdxx

(2.56)

формула Грина для связи двойного и контурного интеграла от непре-

рывной функции двух переменных

;Φ

Φ

2121

21

Qdxdxxx

xx

Q

S

CS























(2.57)

формула Остроградского

 Гаусса связи тройного и поверхностного

интеграла







.Φ ,cos

, , Φ

11321

1

321

dSxnxxx

x

xxx

S













(2.58)

Сферической общностью формул (2.56

), (2.57), (2.58) является то, что в

них интегралы по множеству выражаются через значения на его границах.

Преобразование (2.58

) производят элементарным путем:













,. ,,Φ,,

Φ ,Φcos

32321321

3211

32

dxdxxxxxxx

dxdxdSxn

xxS

xxSS

















(2.59)

и, пользуясь формулой (2.56

), получаем

2. ЭЛЕМЕНТЫ ТЕНЗОРНОГО АНАЛИЗА

2.5. Преобразование Остроградского – Гаусса. Оператор Гамильтона



Гидрогазодинамика. Учеб. пособие 36



.

ΦΦ

,cosΦ

1

32

1

11

1





















d

x

xx

x

dxdSxn

x

(2.60)

Записав формулу Остроградского

 Гаусса для каждой из трех коорди-

нат

x

1

, x

2

, x

3

и умножив на соответствующие единичные орты

321

, , iii





, найдем

ее векторную форму:

 





S

dSnd ,



(2.60а)

где













nxnixnixni







313212111

, cos, cos, cos

и

















3

2

1

x

i

x

i

x

i



некоторый символический дифференциальный вектор, называемый

операто-

ром

Гамильтона (оператором «набла» – от названия древнегреческой буквы



).

Если в формуле (2.60

а) произвести предельный переход при стягива-

нии объема

 в точку, то получим следующее инвариантное определение

оператора Гамильтона:

.

Φ

limΦ

0











dSn



(2.61)

Подобное определение оператора





позволяет вычислить его значение

для любой обобщенной системы координат:













.

Φ

,, Φ,,

limΦ

11

1

321321

322113213211

0

1

q

e

qqq

dqdqeqqqqqqq

q



















(2.61а)

Таким образом,

.

33

3

22

2

11

1

q

e

q

e

q

e





















(2.62)

Пример. Для сферической системы координат

 , ,r

имеем

2. ЭЛЕМЕНТЫ ТЕНЗОРНОГО АНАЛИЗА

2.5. Преобразование Остроградского – Гаусса. Оператор Гамильтона



Гидрогазодинамика. Учеб. пособие 37

.

1

sin

1





















r

e

r

e

r

e

r





(2.63)

Если провести в пространстве эквипотенциальные линии Ф = const, то

производные по касательным к ним будут равны нулю и

.

Φ

constΦ

n









(2.64)

Таким образом, геометрически оператор «набла» означает направление

и величину максимального роста значений. Аналитически

 выражает объ-

емную (по всем трем координатам) производную и служит мерой неоднород-

ности какой-либо величины в пространстве.

2

.

6

.

Т

е

н

з

о

р

н

ы

е

(

о

б

ъ

е

м

н

ы

е

)

п

р

о

и

з

в

о

д

н

ы

е

.

Д

и

ф

е

р

е

н

ц

и

а

л

ь

н

ы

е

о

п

е

р

а

т

о

р

ы

т

е

о

р

и

п

о

л

я

Векторным оператором





можно воздействовать на различные скаляр-

ные, векторные и вообще тензорные величины и получать различные тензор-

ные производные и операторы теории поля, применяемые в математической

теории МЖГ.

Его применение для скаляра дает скалярный градиент

3 ,2 ,1 ,grad

3

1























x

i

x

i





(2.65)

(как уже условились, по дважды встречающемуся (немому) индексу

ведется суммирование от 1 до 3 в

3



).

В результате этой операции получен вектор. Если





умножить скаляр-

но на grad



, то получим скалярный оператор Лапласа

.

grad

2

3

2

1

2

xxx 



















(2.66)

Для вектора

V



можно получить ряд дифференциальных операторов.

Умножая





скалярно на

V



, получим скалярную дивергенцию

2. ЭЛЕМЕНТЫ ТЕНЗОРНОГО АНАЛИЗА

2.6. Тензорные (объемные) производные. Дифференциальные операторы теории поля



Гидрогазодинамика. Учеб. пособие 38

3 2, 1, ,div 







x

V

VV



. (2.67)

Для выяснения геометрического смысла операции

V



div

рассмотрим

 

.

11

321

xxx

dt

D

xxxdt

D







(2.68)

Меняя порядок дифференцирования и учитывая, что

i

V

d

t

dx



, получаем





.div

1

V

x

V

dt

D

i















(2.69)

Таким образом,

V



div

характеризует относительную скорость деформа-

ции объема жидкости или газа.

С другой стороны, пользуясь (2.12

) и (2.32), находим, что

V



div

есть

первый линейный инвариант тензора скоростей деформации.

Умножив





векторно на

V



, получим новый вектор – ротор вектора:

,rot



























 i

x

V

x

V

VV





(2.70)

где



 , ,

чередуются по циклу от 1 до 3.

Геометрический смысл операции

V



rot

можно расширить из рассмот-

рения поля скоростей для абсолютно твердого тела:













rttVtxV

i





0

,

и

















,2 rotrot 



rrrrV

(2.71)

т. е. 1/2rot

V



есть угловая скорость вращения частиц относительно по-

люса 0.

Если

2. ЭЛЕМЕНТЫ ТЕНЗОРНОГО АНАЛИЗА

2.6. Тензорные (объемные) производные. Дифференциальные операторы теории поля



Гидрогазодинамика. Учеб. пособие 39

 gradV



,

то

0gradrot 



. (2.72)

С другой стороны,





.0rot div  VV



(2.73)

Умножив





диадно на

V



, получим тензор 2-го ранга – векторный гра-

диент (дифференциальную диаду):

.3 ,2 ,1 ,Grad 









x

V

VV



(2.74)

Первый линейный инвариант этой диады

.div

1

V

x

V

J











(2.75)

Асимметричная часть этой диады



.3 ,2 ,1 , ,

2

1































x

V

x

V

(2.76)

Сравнивая с (2.70

), устанавливаем, что ее компоненты







,rot

2

1

/







 VV



(2.77)

где



 , ,

равны соответственно 1, 2, 3 (по циклу).

Для тензора 2-го ранга

T с компонентами









3 ,2 ,1 , 



можно по-

лучить вектор

 тензорную дивергенцию  при умножении вектора





слева

на тензор

T:











x

Div



(2.78)

2. ЭЛЕМЕНТЫ ТЕНЗОРНОГО АНАЛИЗА

2.6. Тензорные (объемные) производные. Дифференциальные операторы теории поля



Гидрогазодинамика. Учеб. пособие 40



3 ,2 ,1 , 

и суммирование по



от 1 до 3).

Если же составить внешнее произведение вектора





и тензора T, то

получим тензор 3-го ранга:













x



(







, ,

по циклу от 1 до 3). (2.79)

В МЖГ широко используют следующие тензорные производные и со-

ответствующие операторы:























,вектор Div

,Grad

,вектор rot

,скаляр div

,вектор grad

SV

V

c





(2.80)

где



SV

c





Grad

(симметричная часть дифференциальной диады – тен-

зор скоростей деформации).

2

.

7

.

С

п

р

а

в

о

ч

н

ы

е

д

а

н

ы

е

п

о

т

е

н

з

о

р

н

о

м

у

и

с

ч

и

с

л

е

н

и

ю

1. В трехмерном евклидовом пространстве физические величины

 ха-

рактеристики поля

 можно представлять в виде тензора ранга , имеющего

3

 компонент. Скаляр  можно рассматривать как тензор ранга = 0

(1 компонента), а вектор

V



– как тензор ранга  = 1 (3 компоненты), соответст-

венно тензоры напряжений или деформаций







 SS



 как тензоры 2-го ранга

 = 2 (9 компонент).

2. Если индекс (немой) встречается дважды, то подразумевается сум-

мирование от 1 до 3. Например,



WV





, т. е.



3 ,2 ,1, ,

3

1









WWV

(2.81)

и при этом всегда имеется в виду, что текущий (свободный) индекс (

)

принимает значения 1, 2, 3.

3. Единичному тензору

I соответствует матрица

Кулагин В.А., Грищенко Е.П. Гидрогазодинамика

Подождите немного. Документ загружается.