Курбацкий А.Ф. Лекции по турбулентности. Часть 1
Подождите немного. Документ загружается.


=
∂
∂
⋅+
∂
∂
−
∂
∂
=
∂
∂
⋅=
∂
∂
i
j
j
i
j
j
i
j
j
i
jji
j
x
u
u
x
u
x
u
u
x
u
uuu
x
~
~
)
~
~
(
~
~
~
)
~~
(
.)
~~
2
1
(
~~~~
1
~~
∂
)
2
(2
jj
i
kjkjijj
j
jij
uu
x
uuu
x
ru
∂
∂
+−=
∂
+⋅=
ωε
(1.14)
Вязкий член можно выразить через завихренность
∂
∂
⋅
∂
∂
+
∂
∂
−
∂
∂
∂
∂
=
∂
∂
)
~
()
~
~
(
~
=
2
j
i
x
ν
2
jji
j
j
i
j
j
x
u
xx
u
x
u
x
u
νν
.
~
0
~
+
∂
⋅=
ν
2
j
k
kjiji
j
x
r
x ∂
∂
⋅−=
∂
ω
εν
(1.15)
тановка (1.14) и (1.15) в (1.13) дает
Подс
.
~
~~
)
2
~
(
~
j
k
kjikjkjijj
i
i
x
u
p
xt
u
∂
~~
1
uu
∂
⋅−++
∂
∂
−=
∂
∂
ω
ενωε
ρ
(1.16)
В безвихревом течении
0
~
=
k
ω
по определению, так что вя и
часть инерционного члена с завихренностью исчезают. Инерционный член
в э ами с г
зкий член
че котом случае сводится к градиенту дин о давления
jj
uu
~~
2/1
⋅
ρ
,
авнение (1.16) есть не что иное, как . В турбулент-
ном движении такие условия, конечно, не выполняются.
Член с векторным произведением
kjkji
u
и ур уравнение Бернулли
ω
ε
~~
является решающим в
теории турбулентности. О налогичен кориолисовой силе
kjkji
u Ω⋅⋅
н а
~
~
2
ε
,
которая появ тся в уравнении движения, если система координат враща-
ется с угловой скоростью
k
Ω
~
(множителя 2 в члене с завихренностью нет,
потому что
k
ляе
ω
~
−
это удвоенная локальная угловая скорость малого эле-
мента жидкости). Вихревой член связан также с подъемной силой (эффект
Магнуса), которая действует на вихрев нить ля орост
.
~
j
u
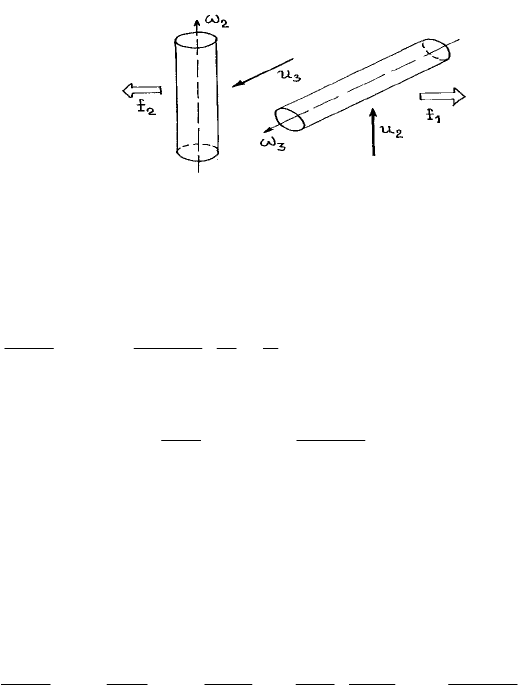
ерпретация вихревой силы дана на рис. 2. В уравнении
для компоненты скорости
1
u
ji
ую в потоке по и
Графическа
член u
ск
я инт
~
kjk
ω
ε
~~
имеет вид
11
).
~~~~
(
2332
ω
ω
uu − Таким образом, векторное произведение завихренность –
скорость генери
232
~~
ω
uf
−
=
.
рует массовые силы
321
~~
ω
uf
=
и
ревая сила», де в потоке жидкости.
Уравнение завихренности. Ур вектора вихря в несжимае-
мой жидкости с постоянными свойст применением пера-
ции «ротор»,
Рис. 2. «Вих йствующая на вихревую нить
авнение для
вами получается о
)/(
qiqp
x
∂
∂
ε
, к уравнению (1.16):
()
×−
−=
∂
qjpqqkpjiqp
p
δδδε
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
∂∂
∂
∂
jj
qi
uu
p
xxt
δ
ρ
ω
~~
2
1
~
~
2
.
~
~~
2
⎟
⎟
⎞
⎜
⎜
⎝
⎛
∂∂
∂
−
∂
∂
×
q
k
kj
q
xx
u
x
ω
νω
(1.17)
Здесь использов ное тождество .
qjpkqkpjkjiiqp
⎠
j
ано тензор
δ
δ
δ
δ
ε
ε
−
=
⋅
Член с давлением в уравнении (1.17) равен нулю, потому что он включает
произведение антисимметричного тензора
iqp
ε
и симметричного тензор-
оператора
(а это дает нуль оведя в уравнени
ного
и (1.17)
qi
xx ∂∂∂ /
2
!). Пр
свертку «дельт» Кронекера по индексам, последнее можно привести к виду
kk
p
k
k
pk
p
k
k
pp
u
∂
∂
∂
ω
ω
k
xxxxx
u
xt ∂∂
∂
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
∂
∂
−
∂
⋅−
∂
=
∂
ω
ν
ω
νω
~
~
~
~
~
~
~
2
. (1.18)
асти (1.18) равен нулю, п ость
имеет нулевую дивергенцию:
Третий член в правой ч отому что завихренн
12
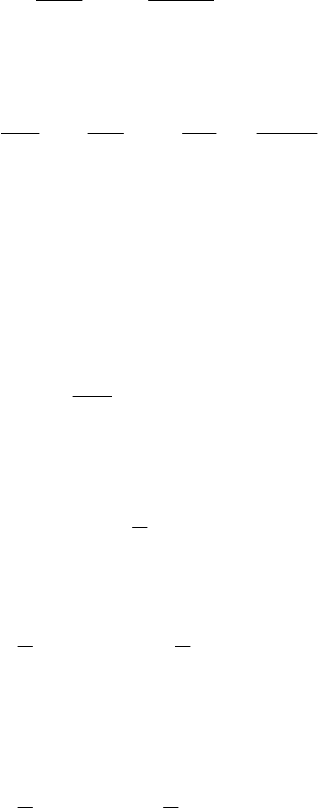
.0
~
~
2
=
∂∂
∂
⋅≡
∂
∂
j
ji
k
xx
u
x
ε
ω
ki
k
k
(1.19)
ение для завихренности имеет вид (и
енен
индексом
а индекс индексом для удобства):
Окончательно уравн ндекс
p
зам
i
, k j
~
~
~
~
~
.
~
2
x
с
ет ие зави
в и Прежде ра-
этого о ка лад
кососимметрической части
скорости деформации xu
jj
i
j
i
j
j
i
j
i
xxx
u
u
t ∂∂
∂
+
∂
∂
⋅=
∂
∂
+
∂
∂
ω
νω
ω
ω
(1.20)
Первый член в правой части уравнения (1.20) не имеет ебе подобного в
уравнении импульса и да своеобразное изменен хренности,
имеющее первостепенную важность турбулентност . чем об
титься к физическому смыслу члена, полезн по зать, что вк
ji
r
~
ji
∂
∂
/
~
равен ну-
лю. Для этой цели разложим
ji
xu
∂
∂
/
~
на две части и такие, что
ji
r
~ ~
ji
s
jijjij
j
i
rs
u
~~~~
j
x
~
~
ωωω
+=
∂
∂
⋅
. (1.21)
1.12) тензора вращения
r
~
Согласно определению (
ji
второй член в (1.21)
имеет вид
kjkjijij
r
ωωεω
~~
2
1
~~
⋅⋅−=
. (1.22)
немые индексы, их можно помен
Поскольку j и k − ять местами, что да-
ет
kjjkikjkji
ωωεωωε
~
2
1
~
2
1
⋅−=⋅ . (1.23)
Снова пер
~
−
еставляя индексы
и вj k
kji
ε
, получим противоположный
знак у величины
i kj
ε
, потому что этот тензор антисимметричный. Следо-
вательно,
kjkjikjkji
ωωεωωε
~~
2
1
~~
2
1
⋅⋅=⋅−
. (1.24)
13

Это равенство может быть справедливым только при обращении его в
ого только первый член в правой част
завихренности можно теперь записать
нуль. В силу эт и (1.21) отличен от
нуля. Уравнение в виде
jj
i
jij
j
i
j
i
xx
s
x
u
t ∂∂
∂
+⋅=
∂
∂
⋅+
∂
∂
ω
νω
ωω
~~~
. (1.25)
Член
jij
s
~~
~~~
2
ω
в уравнении (1.25) представляет собой усиление и вращение
вектора завихренности под воздействием скорости деформации
.
~
s О
ji
ме-
тим, что уравнение (1.25) может б ть получено применением операции
«ротор» непосредственно к уравнению Навье
− Стокса форме (1.1).
Завихренность может, по-видимому, усиливаться пос
т
ы
в
редством ее рас-
тяжения скоростью деформации (
ji
s
~
> 0). С другой стороны, завихрен-
ность должна уменьшаться там, где возникает сжатие (
0
~
<
ji
s ).
Этот источник, ил для завихренности представляет наи лее -
тересный член уравнения завихренности. Существенно, что этот член об-
ращается в нуль для двухмерного течения. Предположим, что течение про-
исходит в плоскости
),(
2
x . Тогда компоненты вектора вихря
1
~
и сток, бо ин
x
1
ω
и
2
~
ω
равны нулю, так что отличн нуля компонентой вектора завихренности
3
~
ой от
остается компонента
ω
. Член, описывающий растяжение вихрей, имеет
всего одну компоненту,
33
~~
i
s
⋅
ω
. Однако в двухмерном течении только
)
~
(
~
2112
ss = ,
11
~
s и
22
~
s могут быть отличны от нуля. Ясно, что двухмерное
течение может вращать или растягивать вектор завихр ност
Простейшей иллюстрацией растяжения вихрей мо служить уско-
ряющееся течение (рис. 3). Здесь продольная компонен ости дефор-
мации
11
не ен и.
жет
та скор
~
s положительна, следовательно, мпоненты
22
ко
~
s и
33
~
s
должны
быть отрицательны, чтобы уравнение неразрывности
)0
~
(
=
ii
s
удовлетво-
рялось. В таком течении завихренность
1
~
ω
возрастает растя-вследствие
жения вихрей, в то время как компоненты завихренности
2
~
ω
и
3
~
ω
умень-
шаются.
Изменение завихренности благодаря растяжению вихрей есть следствие
сохранения момента импульса. При растяжении элементарного материаль-
ного объема его площадь поперечного сечения и момент инерции умень-
14
шаются. При этом компонента угловой скорости в направлении растяже-
ния должна возрастать в силу сохранения момента импульса. Растяжение
вих
ре вихревой нити – тонкого бесконечно длинного ци-
индра, вращающегося вокруг оси. Распределение завихренности по попе-
ичной от нуля можно рассматривать как совокупность непрерыв-
но делен нитей. В
рей всегда ведет к изменению линейного масштаба, как это иллюстри-
руется на рис. 3. Для более полного знакомства с кинематикой завихренно-
сти следует обратиться к руководствам по гидродинамике.
Рассмотрим эффекты растяжения (сжатия) и
вращения вектора завих-
ренности на приме
л
речному сечению вихревой нити для дальнейшего обсуждения полагается
несущественным.
Рис. 3. Растяжение вихрей в аэродинамической трубе с сужением («фильтром»).
Если не принимать во внимание эффекты вязкой диффузии в уравнении
(1.25), вихревая нить движется вместе с жидкостью согласно теореме
Кельвина о сохранении циркуляции. Вихревая пелена – это «оболочка»
вихревой нити. Следовательно, конечную часть жидкости с завихренно-
стью отл
распре ных вихревых ихревые нити индуцируют
безвих-
ревое поле скорости в других точках пространства согласно закону Био −
Савара.
Если
α
≠i , например,
2,1
=
=
α
i
, пер в правой части урав-
нения (1.20) описывает обмен завихренностью между компонентами век-
тора вихря, потому что градиент скорости,
21
/
~
xu
вый член
∂
∂ , отклоняет вихревую
15

нить от ее первоначального положения в направлении оси
2
x , вследствие
чего она приобретает компоненту завихренности в направлении оси
1
x (рис. 4). Если
α
=
i (например, равно 2), вихревая нить растягивается
(рис. 5) под влиянием аксиальной деформации растяжения, без какого-
либо изменения в направлении других осей координат. В пренебрежении
вязкой диффузией (и, строго говоря, требуя сохранения поперечного сече-
ния нити круглым для исключения возникновения крутящег момента си-
ви
ти.
о
лы) вихревая нить сохраняет свой момент импульса,
constr =
2
ω
. В та-
ком случае уменьшение площади поперечного сечения нити под воздейст-
вием аксиального растяжения должно сопровождаться возрастанием за-
хренности (угловой скорости ее вращения).
Рис. 4. Деформация вихревой нити Рис. 5. Аксиальное растяжение
под влиянием сдвига скорости. вихревой нити.
При высоких числах Рейнольдса вязкая диффузия мала и нелинейный
член в уравнении (1.25), описывающий взаимодействие завихренности с
градиентом скорости, может изменить первоначально простую (но трех-
мерную!) структуру течения в невообразимо сложное распределение за-
вихреннос
Таким образом, для описанной качественной картины растяжения вих-
рей и интенсификации завихренности, первостепенное значение имеет
трехмерность. В
мгновенном двухмерном течении вектор скорости дви-
жения. жидкости повсюду направлен параллельно плоскости, и нелиней-
ный член
.0)/
~
(
~
≡
∂
∂⋅
αα
ω
xu
i
Это означает, что хотя большинство неус-
тойчивых бесконечно малых возмущений в установившемся двухмерном
сдвиговом течении являются двухмерными бегущими волнами, усиленные
возмущения достаточно большой амплитуды («пакеты» вихревых нитей)
16
сами оказываются неустойчивыми относительно бесконечно малых, но
трехмерных возмущений. Малое перекручивание участка прямолинейной
вихревой нити искажается и усиливается полем скорости, индуцирован-
ным самим вихрем. Если числа Рейнольдса велики, то вязкая диффузия
мала и искажение будет продолжаться неограниченно. Первоначально не-
уст
слу-
чай
нем возрастать.
аться.
фицируются те вихри, оси которых в любой
данный момент времени располагаются почти параллельно главной (поло-
ойчивые возмущения достигают достаточно большой амплитуды. До-
вольно быстро они становятся
все более и более сложными и неустойчи-
выми, потому что растяжение и отклонение вихревой нити от «прямоли-
нейного направления» индуцируются как полем скорости самих вихревых
нитей, так и основным сдвиговым течением.
Простой способ истолкования того, как возникает непериодическая не-
устойчивость, основан на том факте, что реально волновые числа первона-
чальных возмущений
, так сказать, слегка неустойчивы. Процент неустой-
чивости волнового числа возмущения первой гармоники, грубо говоря,
вдвое выше основной гармоники, и так далее для высших гармоник. При
этом появляются возмущения, имеющие как сумму, так и разность волно-
вых чисел, вследствие нелинейности взаимодействия различных пакетов
вихревых нитей посредством поля скорости, индуцируемого ими самими.
Спектр волновых чисел получается в конечном счете непрерывным. По
мере усложнения картины движения начинают действовать эффекты
ности процесса, описываемые теоремой случайных блужданий: части-
ца, подверженная воздействию случайного импульса, будет в среднем уве-
личивать расстояние, пройденное от места старта (так называемая задача о
«пьяном моряке»). Очевидно, что расстояние между двумя
случайно дви-
жущимися (деформируемыми) частицами будет в сред
Если эти две частицы располагаются на конце элемента вихревой нити,
то в поле течения, близком к полю случайных возмущений, длина элемента
нити будет в среднем увеличиваться, а его завихренность будет возрастать
вследствие растяжения. Очевидно, что и диаметр вихревой нити в рассмат-
риваемой
простой модели будет также уменьш
Изложенная выше картина отвечает основному механизму развитой
турбулентности, а именно: взаимодействие запутанных вихревых нитей,
поддерживаемое случайными флуктуациями завихренности и скорости, и
перенос завихренности к меньшим и меньшим линейным масштабам по-
средством механизма случайных блужданий.
Остается еще представить себе качественную картину описанного про-
цесса переноса «от
начала до конца». Под воздействием средней скорости
деформации флуктуирующая завихренность сама подвержена деформации,
под влиянием которой интенси
17
жи
нит
но
етиче
ия то
тельной) оси скорости деформации (см. об этом также в разд. 2.3).
Вследствие нелинейности процесса интенсификации завихренности турбу-
лентности растяжение преобладает над сжатием. (Доказательство этого
утверждения дано в разд. 3.5).
Таким образом, средняя скорость деформации способствует поддержа-
нию (и сохранению) высокого уровня флуктуаций завихренности. Более
строгое рассмотрение эффекта средней скорости деформации на процесс
трансформации завихренности дано во второй части лекций. Однако из
изложенной выше картины ясно, что уменьшение диаметра вихревой и
в процессе ее растяжения ограничивается вязкой диффузией завихрен -
сти вдали от оси вихря. Растяжение вихрей ведет к увеличению кин -
ской энергии вращен вихревой нити, есть к увеличению энергии
флуктуационного движения. Момент импульса
− порядка величины
2
r
ω
,
и, если он сохраняется, то энергия, имеющая порядок величины
22
r
ω
,
увеличивается, когда
r
уменьшается, а
ω
растет. Кинетическая энергия
черпается из среднего движения, которое инициирует растяжение под воз-
действием средней скорости деформации, так что энергия передается к
движениям все меньших и меньших масштабов посредством вихревых ни-
тей. Процесс наимень-
ших масштаб (за счет
раб
в описании и анализе
структуры тур стей и газов
обладают шир енных сверху
хар
, а именно погран
ом слое переносят
у
неквадрати
передачи энергии продолжается вплоть до самых
ов, на которые воздействие молекулярной вязкости
оты, выполняемой
вязкими напряжениями) становится уже непосредст-
венным.
1.4. Структура развитой турбулентности
Динамика движения жидкости при больших числах Рейнольдса харак-
теризуется существованием турбулентных движений различных масшта-
бов, часть из которых играет специфическую роль
булентности. Турбулентные движения жидко
оким спектром линейных масштабов, огранич
актерным размером области, занятой турбулентной средой, а снизу –
диффузионным действием молекулярной
вязкости.
1.4.1. Макромасштабы турбулентности
Рассмотрим макромасштабы турбулентности на примере конкретного
турбулентного течения ичного слоя (рис. 6). Турбулент-
ные вихри в пограничн дефицит импульса на некоторое
расстояние от обтекаемой твердой поверхности. Пусть характерная турб -
лентная скорость равна
u
ˆ
. Можно полагать её равной сред чной
18
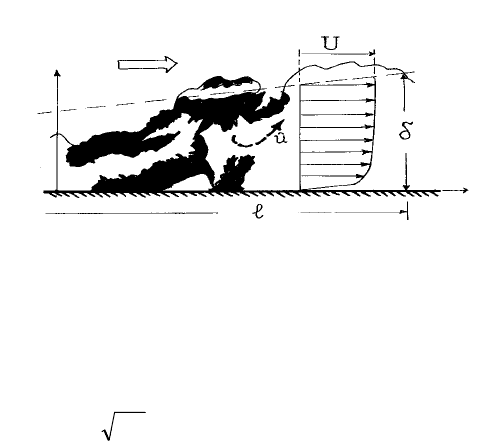
флуктуации скорости
2/1
)3/1( ><⋅
ii
uu , осредненной по толщине погра-
ничного . Если скорость турбулентных флуктуаций равна величине
u
ˆ
,
то толщ слоя растет, грубо говоря, как
udtd
ˆ
/
слоя
ина пограничного
∝
δ
. Ин-
тервал времени, прошедшего от точки начала погр ного слоя до сечеанич
ния, расположенного на расстоянии
вниз по потоку, к ве-
личины
лучить
оценку
-
l имеет порядо
Ul/
(конвективный временной масштаб), так что можно по
.)/(
ˆˆ
Ulutu
⋅
∝⋅∝
δ
турбулентный «диффузионный
В действительности этой оценкой приравнены
» масштаб времени
u
ˆ
/
δ
и конвективный
Рис. 6. Масштабы длины и в турбулентном пограничном слое на глад-
−
скорости
кой непроницаемой поверхности:
скорость внешнего потока; Ul / − вре-
мя, через которое жидкость, находившаяся в начале пограничного слоя, оказывает-
ся на расстоянии
l от него
U
;
δ
− аничног
ламинарн граничного слоя где диффузионный
масшта
толщина погр о слоя.
временной масштаб течения
./Ul
Такая же процедура может быть ис-
пользована и для ого по ,
δ
б
растет как t⋅
ν
, и с учетом
Ult /≅
для отношения диффу-
зионного (поперечного) к конвективному (продольному) масштабу полу-
чается выражение
2/1−
.))(/(/
2/1
=⋅≈ eRUll
νδ
Таким образом, для отношения характерных макромасштабов турбу-
лентного пограничного слоя имеет место связь вида
Ulu /
ˆ
/
∝
δ
. (1.26)
Соотношение между масштабами времени (1.26) представляет собой
фундаментальное допущение: в ситуации с наложенным внешним течени-
19
ем турбулентность, будучи частью самого течения, должна иметь харак-
терный временной масштаб, соизмеримый с временным масштабом тече-
ния. Это противоречит концепции локальной связи между турбулентными
напряжениями и средней скоростью деформации (см. подробнее в разд. 2.2
и 2.3). Однако й временной
масштаб. Мел ого меньший
хар
ких по-
лей
булен
автоматически приспосабливаются к величине
вяз
не вся турбулентность имеет такой большо
комасштабные турбулентные вихри имеют мн
актерный временной масштаб, вследствие чего их осредненные харак-
теристики проявляют тенденцию к статистической независимости от ос-
редненного движения.
1.4.2. Микромасштабы турбулентности
Крупные вихри турбулентности в наибольшей степени ответственны за
перенос различного рода скалярных свойств термогидродинамичес
. Грубо говоря, размер крупных вихрей сравним с характерным разме-
ром области, занятой турбулентностью. Размер
этих вихрей представляет
собой характерный линейный масштаб при анализе взаимодействия турбу-
лентности со средним течением. Для некоторых других аспектов динамики
турбулентности необходимы, однако, другие линейные масштабы.
На очень малых расстояниях молекулярная вязкость эффективно сгла-
живает тур тные флуктуации скорости. Генерация мелкомасштабных
флуктуаций обусловлена нелинейными членами в уравнениях движения.
Вязкость жидкости предотвращает генерацию
вихрей бесконечно малых
размеров путем рассеяния энергии мелкомасштабных вихрей в молекуляр-
ное движение. Это связано с наличием в уравнении Навье − Стокса малого
параметра
eR/1 с сингулярным поведением при больших числах Рей-
нольдса. Можно полагать, что при больших числах Рейнольдса эффекты
вязкости становятся исчезающе малыми, но нелинейные члены уравнения
движения противодействуют этой угрозе, генерируя турбулентные движе-
ния достаточно малых линейных масштабов. Тем самым движения наи-
меньших масштабов сами
кости жидкости. Как
только характерный масштаб поля течения стано-
вится столь большим, что эффекты вязкости оказываются пренебрежимо
малыми, течение создает вихри малых масштабов, сохраняя тем самым
эффекты вязкости (в частности, скорость диссипации энергии турбуленто-
сти) на конечном уровне.
Так как мелкомасштабные турбулентные вихри стремятся иметь малые
временные масштабы (которые можно ассоциировать с частотой вращения
таких вихрей), можно предположить, что эти вихри статистически незави-
симы от крупномасштабных, энергонесущих вихрей и среднего движения.
Если это допущение справедливо, динамика мелкомасштабных вихрей
20
