Курбацкий А.Ф. Лекции по турбулентности. Часть 1

Подождите немного. Документ загружается.

может зависеть только от скорости, с которой они снабжаются энергией,

передаваемой от крупномасштабных вихрей, и от молекулярной вязкости.

Допустимо также предположить, что скорость подвода энергии к мелко-

масштабным вихрям, в которых сосредоточена наибольшая часть диссипи-

руемой энергии, равна скорости диссипации. Это основывается на том, что

результирующая скорость изменения энергии мелкомасштабных

вихрей

свя

ния лежат в основе

фундаментальной теории локально-изотропной турбулентности А.Н.Кол-

могорова

держа-

щих вихрей

под

действием

зана с характерным временным масштабом течения в целом, и поэтому,

данная скорость будет малой по сравнению со скоростью диссипации

энергии турбулентности. Эти физические соображе

(1941 г.).

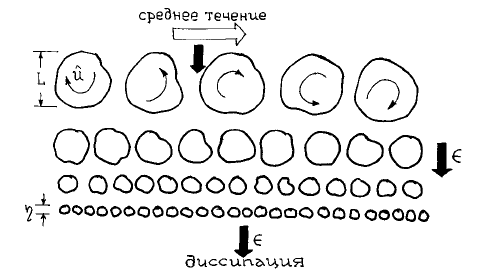
Схематически картина передачи энергии от крупных энергосо

к мелкомасштабным вихрям в

процессе дробления вихрей

механизма растяжения показана на рис. 7.

Рис. 7. Каскадный процесс трансформации энергии турбулентности.

− ли-

нейный масштаб энергонесущих вихрей;

− линейный масштаб наименьших

вихрей.

Изложенные сообр ения основываются на предположении, что в чис-

ло определяющих пара етров мелкомасштабного движения входят по

крайней мере скорость диссипации кинетической энергии турбулентност

аж

массы жидкости

3−

), и кине-

, имеющая размерность (см

в единице

матическая вязкость

, имеющая размерность (см

1−

). Из опреде-

ляющих величин

могут быть образованы следующие масштабы

длины, времени омасштабного турбулентного движения:

νη

= )

и скорости мелк

4/1

.)(,)/(

4/12/1

ενεντ

⋅== v

(1.27)

Эти масштабы называют микромасштабами длины, времени и скорости

турбулентности. Число Рейнольдса, составленное из этих масштабов,

равно единице:

.1/)( =⋅=

νη

veR Это означает, что мелкомасштабное дви-

жение оказывается вполне вязким и что вязкая диссипация сама приспо-

сабливается к подводимой энергии посредством регулируемых масштабов

длины.

Невязкая оценка скорости диссипации энергии турбулентности.

Можно лучше понять различие между крупномасштабным и мелко-

масштабным турбулентными движениями, если связать скорость диссипа-

ции энергии турбулентности

с характерным сштабами энергосодер-

жащих вихрей. Возможное допущение состоит в том, чтобы рассматривать

скорость, с которой крупномасштабные вихри снабжают энергией мелко-

масштабные вихри, пропорциональной обратной величине характерного

масштаба времени энергосо

и ма

д ащих вихрей

(см. рис. 7). В п. 1.4.3

ерж

характерному размеру энергосодержащих вихрей дано точное количест-

венное определение как интегрального масштаба турбулентности, вычис-

ляемого в виде интеграла от двухточечной корреляционной функции тур-

булентного поля скорости.

С учетом принятого допущения, количество кинетической энергии в ед.

массы жидкости, вовлеченной в крупномасштабное движение, пропорцио-

нально величине

и скорость передачи энергии от крупных вихрей к ма-

лым вихрям получается порядка величины

/(/

uLu

Эта энергия со-

гласно теории Колмогорова диссипируется в энергию молекулярного дви-

жения мелкомасштабными вихрями со скоростью

. Таким образом, со-

гласно теории Колмогорова все три скорости трансформации энергии –

пос ения к энерг

да вихрям и

тупления от среднего движ онесущим вихрям (см. рис. 7) ,

пере чи ее по спектру дробящихся вихрей к диссипативным

вязк диссипации – принимаются равными. Следовательной о, скорость

диссипации энергии турбулентности определяется выражением

Lu /

⋅=

βε

, (1.28)

где

− постоянный численный множитель порядка единицы.

Во 2-й части «Лекций…» показывается, что в неравновесных ситуациях возможно

замедление в спектральном переносе энергии, и, следовательно, отмеченное равен-

ство трех скоростей трансформации энергии при спектральном переносе может и

не соблюдаться (неравновесная турбулентность).

Это выражение устанавливает, что диссипация энергии турбулентности

вследствие вязкости может быть выражена через параметры, связанные с

крупномасштабными вихрями, динамика которых непосредственно от вяз-

кости не зависит. Диссипация представля пассивный процесс, если

иметь в виду, что он протекает со скоростью диктуемой невязким, инерци-

онным поведением крупномасштабных вихрей. Оценка (1.28) – краеуголь-

ный

камень предположений теории турбулентности. Она требует, чтобы

энергонесущие, крупномасштабные вихри теряли большую часть своей

кинетической энергии, равной величине

)2/1( u

, в пределах одного «цик-

ла времени»

. Это означает, что нелинейный механизм, который пре-

вращает крупные вихри в вихри меньшего размера, допускает у энергосо-

держащих вихрей такое же диссипативное время, как и их характерное

время. Другими словами, турбулентность есть сильно нелинейная сто-

хастическая система с быстрой диссипацией энерги жно думать, что

это свойство турбулентности как-то связано

с концепцией производства

энтропии, заключенной во втором начале термодинамики. Следует, одна-

в виду, что крупномасштабные вихри теря ренебрежимо ма-

лую долю своей энерги х эффектов вязкой диссипации. Мас-

штаб времени вязкого затухания порядка величины

, так что потеря

энергии крупными вихрями вследствие вязкости протекает со скоростью

u⋅

ет собой

и. Мо

ко, иметь ют п

и из-за прямы

циент

, которая мала по сравнению с величиной

Lu /

, если турбулент-

ное число Рейнольдса

( LueR

⋅= велико. Нелинейный механизм явля-

ется диссипативным потому, что он создает все меньшие и меньшие вихри

вплоть до размеров вихрей стол малых, что вязкая диссипация кинетиче-

ской энергии становится почти непосредственной.

Основное положение современной теории турбулентности (1.28) име-

ет в своей основе надежное экспериментальное подтверждение. Рисунок 8.,

заимствованный из книги Бэтчелора [1], показывает, что

в выражении

(1.28) численный коэффи

приб единице (

з ической трубе, выполненная

ринивасаном

и показанная на рис. 9, свидетельствует о том, что для зна-

лиженно равен хотя име-

ется разброс значений безразмерной скорости диссипации от 0,8 до 1,4).

Недавняя обработка экспериментальных данных о затухании однород-

ной турбулентности а решеткой в аэродинам

Sreenivasan, K.R. On the scaling of the turbulence energy dissipation rate // Physics of

Fluids, 1984. Vol. 27. P. 1048.

чений числа Рейнольдса > 50 величина

νλ

( ⋅= ueR

⋅

()L

оказыва-

тся постоянной и приближенно равной единице (микромасштаб турбу-

ентности Тэйлора

определен в разд. 3.3).

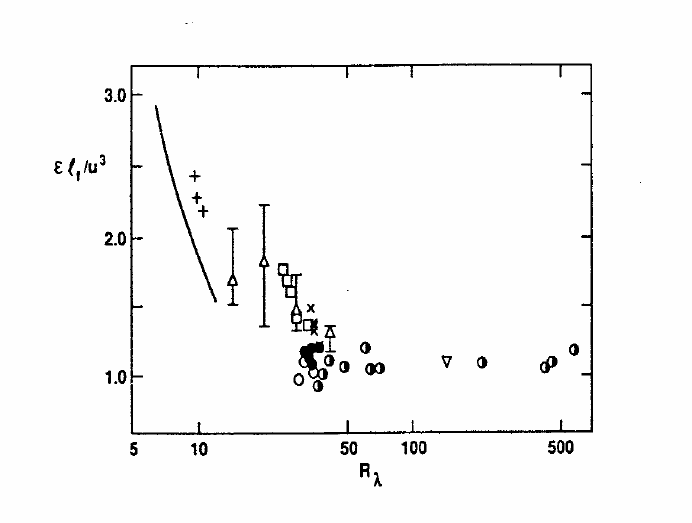
ис. 8. Поведение безразмерной скорости диссипации энергии в затухающей

однородной турбулентности за решеткой в аэродинамической трубе:

− про-

дольный интегральный масштаб турбулентности;

− ха-

рактерная скорость турбулентных вихрей.

2/1

))(3/1( ><=

ия

однородной турбулентности за решеткой в аэродинамической трубе: масштаб

−

себя внимание крайне нерегулярный, перемежающийся характер течения у

Рис. 9. Безразмерная скорость диссипации для начального периода затухан

продольный интегральный масштаб турбулентности;

R − число Рейнольдса.

Экспериментальные визуализации реальных турбулентных тече-

ний в пограничном слое у гладкой твердой поверхности и в круглой

струе. Рисунок 6 представляет собой лишь схематичную, а не истинную

картину течения в пограничном слое у гладкой твердой поверхности. На

рис. 10 показана визуализация структуры турбулентности пограничного

слоя, полученная введением мелких капелек масла внутрь ламинарного

пограничного

слоя через пол рабочей части аэродинамической трубы, по-

сле чего слой искусственно турбулизовался. Световой нож демонстрирует

структуру течения на некотором расстоянии вниз по потоку. Обращает на

внешней границы пограничного слоя (чередование турбулентных и потен-

циальных форм движения среды в фиксированной точке в разные моменты

ремени).

турбулентности пограничного слоя на твердой

непроницаемой поверхности

Рис. 10. Визуализация структуры

Рис. 11. «Типичный вихрь» в турбулентном пограничном слое

Воспроизведено по книге Милтона ван Дайка: Дайк М., ван. Альбом течений жид-

кости и газа. М.: Мир, 1986. С. 94, рис. 158.

Там же. С. 97, рис. 162.

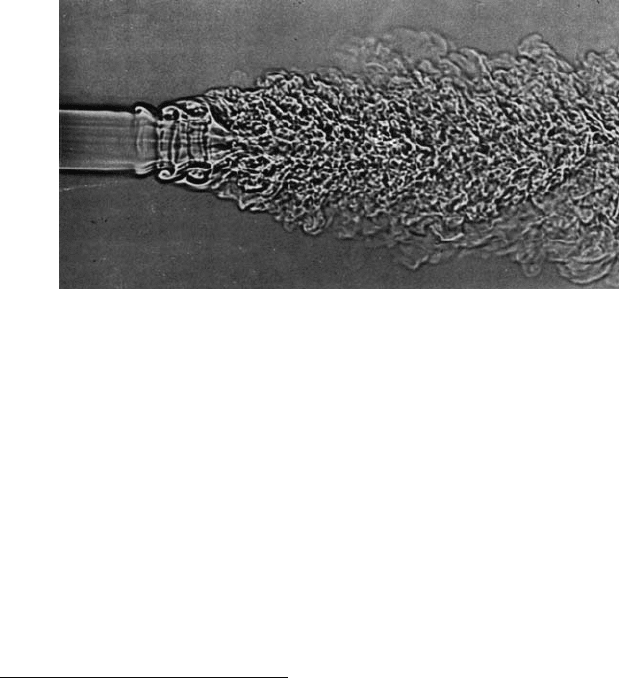
Рисунок 11 показывает одну их немногих замечательных визуализаций

структуры реального турбулентного пограничного слоя, зафиксировавшей

типичный турбулентный вихрь. На этом рисунке масляный туман освеща-

ется лазерным световым ножом, фиксируя, структуру типа вихревого

кольца справа, чуть ниже и правее центра снимка, похожую на разрезан-

ный и наклонившийся влево гриб. Он имеет размеры скорее

порядка не-

скольких пристеночных масштабов длины

)/( u

∗

, а не соизмеримые с

толщиной пограничного слоя (

u − скорость трения на стенке).

∗

Рис. 12. Круглая турбулентная струя

На рис. 12 показана теневая фотография, демонстрирующая структуру

струи углекислого газа, вытекающую из сопла диаметром 6,35 см в воздух,

при скорости 38,7 . В начале истечения из сопла, когда число Рей-

нольдса Re=30000, струя ламинарна. На расстоянии одного диаметра от

сопла отчетливо фиксируется неустойчивость с последующим образовани-

ем вихревых колец и переход к состоянию турбулентного движения. Хо-

рошо видна турбулентная, вихревая структура струи. Струя, вытекающая

при том же числе Рейнольдса из сопла большего диаметра (

т. е. с большим

интегральным масштабом турбулентности) имела бы более «крупнозерни-

стую» мелкомасштабную структуру (см. об этом также в п. 1.4.3).

1−

⋅см

Дайк, М., ван. Указ. соч. С. 72, рис. 117.

Изложенная выше концепция переноса энергии турбулентности от

крупных вихрей к мелким базировалась на качественном понятии турбу-

лентного вихря. Во 2-й части «Лекций…» этому понятию дано более точ-

ное определение.

Отношения масштабов.

Подстановкой (1.28) в (1.27) можно получить

следующие отношения для масштабов:

(1.29)

,Re)/)

()/(

4/3

−

=⋅=

LuL

νη

(1.30)

,Re)/)

((/)

(

2/1

−

=⋅=⋅

LuLu

ντ

(1.31)

.Re)/)

(()

4/1

−

=⋅=

Luuv

Эти отношения показывают, что масштабы длины, времени и скорости

мелких вихрей много меньше тех же масштабов крупных вихрей, причем

разделение в масштабах растет с увеличением числа Рейнольдса. Следова-

тельно, статистическая независимость и состояние динамического равно-

весия мелкомасштабной структуры турбулентности должны быть более

очевидными при очень больших числах Рейнольдса.

Главное отличие

двух турбулентных течений с различными числами

Рейнольдса, но с одинаковым интегральным масштабом заключается в ве-

личине наименьших вихрей. Турбулентное течение при относительно низ-

ком числе Рейнольдса имеет относительно крупную мелкомасштабную

структуру.

Визуальное свидетельство мелкомасштабной структуры можно обна-

ружить, если в турбулентном течении имеются температурные флуктуа-

ции. Градиенты температуры и показатель

преломления оказываются наи-

более крутыми, если они связаны с наименьшими вихрями. Любая оптиче-

ская система, которая чувствительна к таким флуктуирующим градиентам,

«видит» мелкомасштабную структуру турбулентности. Дрожащий, «нерв-

ный» горизонт, видимый в теплый день, представляет собой хорошую ил-

люстрацию этого явления.

Завихренность (ротор вектора скорости) имеет размерность частоты

Завихренность мелкомасштабных вихрей пропорциональна обратной

величине масштаба времени

1−

. Из (1.30) можно заключить, что завихрен-

ность мелкомасштабных вихрей много выше, чем крупномасштабных вих-

рей. С другой стороны, (1.31) означает, что энергия малых вихрей мала по

сравнению с энергией крупных вихрей. Это типично для турбулентности:

большая часть энергии связана с крупномасштабным движением, наи-

большая завихренность связана с мелкомасштабным движением.

1.4.3. Турбулентная диффузия, лагранжевые корреляции,

спектр и динамика мелкомасштабной вихревой структуры

Турбулентная диффузия жидких частиц. Лагранжевые корреляции.

Рассмотрим процесс диффузии, создаваемый непрерывными перемеще-

ниями жидких частиц только вдоль оси

в предположении, что осред-

ненная скорость потока в этом направлении равна нулю. Движение жидкой

частицы происходит под действием турбулентных пульсаций скорости.

Пусть частица покидает источник в момент времени

. Тогда её поло-

жение в момент времени

будет определяться по формуле t

(1.32)

,)(

tdtX

′′

∫

где

− лагранжевая скорость перемещающейся частицы.

(Здесь делается различие между эйлеровой координатой точки пространст-

ва и лагранжевой координатой движущейся частицы). Для дальнейшего

следует выяснить вопрос о том, когда скорость случайно блуждающей час-

тицы может быть стационарной функцией времени. Ограничимся замеча-

ниями качественного характера.

dtdXv /

Если все статистические характеристики турбулентности не изменяют-

ся с течением времени, то турбулентность

является стационарной. Если

турбулентное течение к тому же еще и однородно, то в таком случае ско-

рость блуждающей частицы будет случайной стационарной функцией.

В неоднородном и безграничном в направлении неоднородности тече-

нии перемещающаяся частица блуждает в области течения со все более

различающимися характеристиками. Например, в пограничном слое у

твердой поверхности частица

будет постепенно удаляться от поверхности

во внешнюю часть пограничного слоя, где свойства турбулентности отли-

чаются от тех, в которых частица находилась первоначально. В таком те-

чении скорость частицы не будет стационарной функцией. С другой сто-

роны, в ограниченном течении, например развитом турбулентном течении

в круглой трубе, скорость частицы будет случайной

стационарной функци-

ей, поскольку в этом течении частица в процессе блуждания испытывает

«отражение» от стенки трубы. Следовательно, скорость случайного блуж-

дания жидкой частицы стационарна, если само течение стационарно и ог-

раничено по всем направлениям неоднородности.

Если турбулентное течение статистически стационарно и однородно, то

выражение (1.32) можно осреднить по большому числу частиц,

испущен-

ных источником (в точке с координатой

X ) в последовательные мо-

менты времени. Результирующее среднее значение координаты частицы

будет при этом равно нулю, поскольку скорость − случай-

ная функция времени.

)(

Умножив выражение (1.32) на скорость частицы

, получим )(

tdtvtvX

tXtvtX

′′

∫

⋅=

⎟

⎠

⎞

⎜

⎝

⎛

=⋅=⋅ )()(

)()()(

222

. (1.33)

Осреднение выражения (1.33) по многим частицам дает скорость диспер-

сии смещения жидкой частицы

∫

′

⋅<=

tdtvtvX

.)()(

(1.34)

Поскольку турбулентность предполагается статистически стационарной,

корреляционная функция скорости

′

⋅

)()(

tvtvR

должна быть

функцией разности моментов времени

.tt

′

−

(Индекс L в этом разделе

отмечает лагранжевые величины, определяемые по данным измерений в

точках траекторий жидких частиц).

Выражение (1.34) удобно переписать, введя безразмерную величину

корреляции, называемую лагранжевым коэффициентом корреляции:

⋅

′

⋅

)()(

)(

tvtv

τρ

(1.35)

Подстановка (1.35) в (1.34) приводит к выражению

∫

><=

dvX

.)(

ττρ

(1.36)

Проинтегрировав (1.36) по времени, получим выражение для дисперсии

смещения жидкой частицы:

(1.37)

∫∫

′

><=><

′

dtdvtX

.)(2)(

ττρ

Интегрирование выражения (1.37) по частям