Курбацкий А.Ф. Лекции по турбулентности. Часть 1

Из выражения (2.29) можно получить, действуя в известной степени

формально, локальную зависимость турбулентных напряжений от прило-

женной средней скорости деформации. Такая зависимость должна быть

сформулирована в наиболее общей форме.

В новейшей механике континуума постулируются принципы, которым

должны удовлетворять определяющие соотношения моделей сплошных

сред. Это принципы

детерминизма, локального действия и материальной

объективности.

Рассмотрим вопрос о соблюдении этих принципов для той

или иной замкнутой модели рейнольдсовых напряжений.

Принцип детерминизма, утверждающий, что напряженное состояние

сплошной среды зависит только от предшествующих ее состояний, соблю-

дается как в ламинарных, так и турбулентных движениях сплошной среды.

Принцип локального действия требует, чтобы взаимодействия между

частями сплошной среды осуществлялись через непосредственный контакт

– от частицы к частице только близкодействием. Предыстория же сказыва-

ется только через последовательные во времени, но смежные части среды.

Перенос свойств в турбулентном течении крупномасштабными вихрями на

расстояния порядка линейного лагранжевого интегрального масштаба тур-

булентности, сравнимого с характерным масштабом

длины среднего тече-

ния, противоречит принципу локального действия.

Принцип материальной объективности требует инвариантности

определяющего соотношения как относительно группы галилеевых преоб-

разований, так и инвариантности относительно неинерциального преобра-

зования к равномерно вращающейся системе отсчета. Первая часть этого

принципа должна, несомненно, выполняться в случае турбулентного дви-

жения. Этот принцип в целом устанавливает, что определяющие соотно-

шения должны быть инвариантными относительно расширенной группы

галилеевых преобразований вида

,)(

*

tcxx

G

+=

(2.30)

которая допускает произвольное трансляционное ускорение c



G

системы

отсчета относительно инерциальной системы координат

.x

G

Эта инвари-

антность при произвольных, зависящих от времени, вращениях и трансля-

циях (переносах) системы отсчета определяется как

,)()(

*

tcxtQx

G

+⋅=

(2.31)

где

− любой, зависящий от времени собственный ортогональный

тензор вращения. Инвариантность определяющих уравнений в новейшей

механике континуума подразумевает их инвариантность относительно

)(tQ

G

51

преобразований (2.31), что и составляет суть принципа материальной объ-

ективности.

В случае молекулярного движения характерное время образования на-

пряжений сдвига,

mm

vT /

ξ

∝

(где

ξ

− средняя длина свободного пробега

молекул, а

− средняя скорость теплового движения молекул), и это

время много меньше обычно наблюдаемых периодов вращения системы

отсчета, исключая, конечно, экзотические случаи вращения со сверхвысо-

кими угловыми скоростями. Указанное различие в характерных масштабах

времени в случае ламинарного движения среды фактически устраняет

влияние преобразования (2.31) на формирование напряжений сдвига, что и

указывает на возможность

выполнения условия инвариантности относи-

тельно преобразования к равномерно вращающейся системе отсчета (част-

ному случаю общего преобразования (2.31)).

m

v

В случае турбулентного движения этот принцип в целом не выполняет-

ся. То есть определяющие соотношения для тензора турбулентных

напряжений не могут быть инвариантными относительно расширенной

группы галилеевых преобразований вида (2.31). Такую инвариантность

можно ожидать для турбулентности

с отношением характерного масштаба

времени турбулентных флуктуаций к характерному масштабу среднего

движения

1/

0

<

L

T

0

T

TT

(в предельном случае одномерной турбулентности).

Однако для общей трехмерной турбулентности это не так. Характерное

время образования турбулентного сдвигового напряжения сравнимо с

лагранжевым интегральным временным масштабом

, и этот масштаб

порядка величины характерного временного масштаба среднего движения

. Таким образом, условие инвариантности относительно преобразования

к равномерно вращающейся системе отсчета в случае турбулентного

движения не может выполняться. Определяющие соотношения для

рейнольдсовых напряжений не могут быть сформулированы в форме,

удовлетворяющей расширенной группе галилеевых преобразований (2.31).

Инвариантность же относительно группы галилеевых трансляций должна

для таких соотношений соблюдаться. Рассмотрение турбулентного

движения сплошной среды

в неинерциальной системе координат возможно

при учете кориолисовых и «центробежных» сил.

Модель рейнольдсовых напряжений, инвариантную относительно

группы галилеевых трансляций, можно записать в виде

52

[

]

.),(,

,,;),(,),(,),(),(),(

tsy

txsyTsyLsxUsyUtx

jiji

∞−∈Ξ∈

−ℑ=

G

τ

(2.32)

Переменные

),(,),(,),(),( syTsyLsxUsyU

G

−

G

могут быть представлены

в виде разложений в ряды Тэйлора:

,)()(

!2

)()(

)(),(),(

2

⋅⋅⋅+

∂∂

∂

⋅−⋅−+

+

∂∂

∂

⋅

−⋅−

+

∂

⋅−=−

i

ii

ji

jjii

i

ii

xt

U

xyts

xx

U

xyxy

x

U

xysxUsyU

G

(2.33)

,)()(

!2

)()(

!2

)(

)()(),(

22

2

22

⋅⋅⋅+

∂∂

∂

⋅−⋅−+

∂∂

∂

⋅

−⋅−

+

∂

⋅

−

+

∂

⋅−+

∂

⋅−+=

i

ii

ji

jjii

i

ii

xt

L

xyts

xx

L

xyxy

t

Lts

t

L

ts

x

L

xyLsyL

G

(2.34)

,)()(

!2

)()(

!2

)(

)()(),(

22

2

22

⋅⋅⋅+

∂∂

∂

⋅−⋅−+

∂∂

∂

⋅

−⋅−

+

∂

⋅

−

+

∂

⋅−+

∂

⋅−+=

i

ii

ji

jjii

i

ii

xt

T

xyts

xx

T

xyxy

t

Tts

t

T

ts

x

T

xyTsyT

G

(2.35)

где сохранены члены вплоть до второго порядка включительно. В этих

разложениях подразумевается, что величины

LU ,

G

и

T

в правых частях

выражений (2.33) – (2.35) вычисляются в точке

.),( tx

G

После расщепления

ji

τ

на изотропную и девиаторную части и использования элементарных

соображений размерности величин получается следующее выражение для

тензора турбулентных напряжений:

,),(,

,,;),(

ˆ

),(

ˆ

3

2

tsy

txsxUsyU

T

L

E

jijiji

∞−∈Ξ∈

⎥

⎦

⎤

⎢

⎣

⎡

−ℑ⋅−⋅⋅=

G

GG

G

δτ

(2.36)

53

где

ii

EU

L

T

U

τ

2

1

,

ˆ

=⋅=

G

представляют собой безразмерную среднюю ско-

рость и кинетическую энергию турбулентности единицы массы жидкости

соответственно. Величина

есть безразмерный функционал своих ар-

гументов, имеющий нулевой след. Используя разложения Тэйлора (2.33) -

(2.35), легко показать, что

ji

ℑ

ˆ

,)(),(

ˆ

),(

ˆ

2

0

2

*

**

0

⎟

⎠

⎞

⎜

⎝

⎛

+

⎟

⎠

⎞

⎜

⎝

⎛

∂

⋅−=−

T

O

x

U

xy

T

sxUsyU

j

i

jjii

GG

(2.37)

где

j

i

j

i

ii

x

U

T

x

U

L

xy

∂

⋅=

⎟

⎠

⎞

⎜

⎝

⎛

∂

−

=−

0

*

**

,

)(

(2.38)

безразмерные переменные – величины порядка единицы, а

− временной

масштаб среднего течения.

0

T

Если предположить, что имеется полное разделение масштабов турбу-

лентного движения, тогда

1/,1/

00

<

< LLTT

(2.39)

и выражение (2.36) может быть локализовано в пространстве и во времени.

Как уже обсуждалось выше, сделанное предположение представляется

слишком большим упрощением. Действительно, если отношение харак-

терных временных масштабов молекулярного движения в большинстве

течений сплошной среды таковы, что

, то для турбулентного

движения указанное отношение может быть величиной порядка единицы.

6

0

10/

−

≤TT

С использованием соотношений (2.37) – (2.39) выражение (2.36) может

быть представлено в виде

,)(

3

2

,

2

lkjijiji

UG

T

L

E ⋅⋅−⋅⋅=

δτ

(2.40)

где

−

⎟

⎠

⎞

⎜

⎝

⎛

∂

⋅=

*

0

,

l

k

lk

x

U

T

U

безразмерный градиент средней скорости. По-

скольку функция

симметрична и имеет нулевой след, так же как и

ji

G

54

функция

lk

U

,

, то в первом порядке по отношению функция

0

/TT

ji

τ

принимает форму, инвариантную относительно галилеевых преобразова-

ний трансляции:

,

3

2

⎟

⎠

⎞

⎜

⎝

⎛

∂

+

∂

⋅−⋅⋅=

i

j

i

Tjiji

x

U

x

U

E

νδτ

(2.41)

где коэффициент

(2.42)

TL

T

/

2

≡

ν

имеет смысл введенного ранее коэффициента

вихревой (или турбу-

лентной) вязкости

(см. формулу (2.25)). В то время как «стандартная»

модель вихревой вязкости (2.42) получается при сохранении членов

первого порядка отношения временных масштабов

, анизотроп-

ные (или вязкопластические) модели вихревой вязкости получаются

при удержании и членов второго порядка. Выражение для вихревой

вязкости остается незамкнутым, пока не указан способ вычисления

функций

и

)/(

0

TT

L

T

в формуле (2.42).

Невязкая оценка диссипации кинетической энергии турбулентности

(1.28) позволяет записать выражение для турбулентной вязкости через

наиболее часто измеряемые параметры

E

и

ε

(Колмогоров, 1942):

(2.43)

,/

2

εν

µ

EC

T

⋅=

где

− коэффициент пропорциональности, численное значе-

ние которого откалибровано при решении многочисленных задач как

для однородных, так и неоднородных турбулентных течений. В двухпа-

раметрической теории турбулентности, изложение которой дано во 2-й

части «Лекций…», величины

09,0≅

µ

C

E

и

ε

определяются из дифференциаль-

ных уравнений переноса.

Изложенная выше процедура «локализации» функционала, опреде-

ляющего тензор турбулентных напряжений, носит, в известной степе-

ни, формальный характер. Однако результирующая тензорно-

инвариантная модель (2.41), как уже выше упоминалось, дает приемле-

мые результаты при описании широкого класса неоднородных турбу-

лентных течений и, кроме того, часто является составным

элементом

других современных методов моделирования турбулентности (см. под-

робнее «Лекции…», часть 2). В таком случае должен существовать и

55

иной, физически более корректный, способ оценки турбулентного по-

тока импульса, приводящий к модели (2.41).

Существование турбулентных напряжений требует, чтобы турбу-

лентные флуктуации скорости

и были коррелированы. Для дан-

ного рассмотрения ради простоты ограничимся уже встречавшимся ра-

нее течением чистого сдвига. В этом течении средняя скорость в на-

правлении оси

отлична от нуля,

1

u

2

u

1

x 0)(

21

≠

xU

, а средние скорости

. Единственная отличная от нуля компонента тензора

турбулентных напряжений ед. объема жидкости в этом течении

− ком-

понента в плоскости течения

0

32

== UU

.

2121

>

<

−

=

uu

ρ

τ

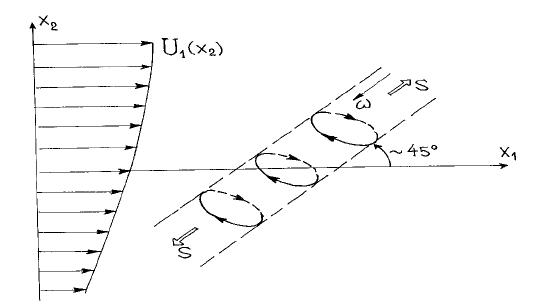
Рис. 16. Трехмерные турбулентные вихри с завихренностью

ω

, подвер-

женные растяжению со скоростью деформации

.S

Энергия вихрей должна поддерживаться средним течением, так как

они непрерывно теряют энергию, переходящую к вихрям меньших раз-

меров. Для восполнения этой потери необходим сдвиг скорости,

, вследствие которого отрицательные значения возни-

кают более часто, чем положительные значения при положительной

флуктуации , и наоборот. Корреляция оказывается величи-

ной отрицательной. Энергосодержащие вихри – это те вихри, которые

наиболее эффективно извлекают энергию из среднего течения. Опыт-

ные данные [4] наводят на мысль, что вихри, наиболее эффективные в

поддержании желательной корреляции между турбулентными флук-

туациями скорости

и и извлечении энергии из среднего течения,

0/

21

>∂∂ xU

1

u

2

u

><

21

uu

1

u

2

u

56

– это те вихри, главные оси которых выстраиваются (приближенно) в

направлении главных осей средней скорости деформации (рис. 16). Ме-

ханизм передачи энергии таким вихрям обусловлен скорее всего растя-

жением вихрей. Когда вихри, изображенные на рис. 16, деформируются

под влиянием сдвига скорости, сохранение их момента количества

движения стремится поддержать хорошую корреляцию между пульса-

циями

скорости и , способствуя тем самым эффективной переда-

че энергии (более детально этот вопрос рассматривается в гл. 3 и части

2-й «Лекций…»).

1

u

2

u

Пусть турбулентность рассматриваемого течения чистого сдвига ха-

рактеризуется одним характерным масштабом скорости и одним ха-

рактерным масштабом длины

.

u

ˆ

L

Коэффициент корреляции между компонентами скорости

и оп-

ределяется величиной

2

u

1

u

21

ˆˆ

uu

c

⋅

><−

=

, (2.44)

где

><=

2

11

ˆ

uu

, ><=

2

22

ˆ

uu

.

Следовательно,

212121

ˆˆ

uuc

⋅

=

ρ

τ

. (2.45)

Опытные данные показывают, что во всех турбулентных течениях со

сдвигом скорости

u

21

ˆˆ

u

∝

. (2.46)

С учетом (2.46) оценку (2.45) можно записать как

(2.47)

,)

ˆ

(

ˆ

2

22121

uc ⋅=

ρτ

где неизвестный коэффициент

в сдвиговых течениях всегда поряд-

ка единицы. Однако в турбулентности, поддерживаемой за счет работы

флуктуирующей силы плавучести, коэффициент

может иметь зна-

чение существенно меньшее единицы. Далее, экспериментальные дан-

ные надежно подтверждают отмеченную выше хорошую корреляцию

между пульсациями скорости

и :

21

ˆ

c

21

ˆ

c

1

u

2

u

.

ˆˆ

4,0

2121

uuuu ⋅⋅≈><−

Изображенные на рис. 16 вихри имеют завихренность порядка величи-

ны

, которую они поддерживают за счет взаимодействия со

средним сдвигом скоро

2

xd

. Следователь

Lu /

ˆ

2

сти

1

/Ud

но,

57

,

ˆ

2

12

xd

Ud

c

L

u

⋅=

(2.48)

где

− безразмерный коэффициент. Если деформирование вихрей –

эффективный механизм, как это предполагается на рис. 16, коэффици-

ент

Действительно, в этом случае характерный масштаб времени

турбулентных вихрей («частота» их вращения),

, и характерное

время среднего течения,

, должны быть величинами одно-

го и того же порядка, потому что турбулентность представляет собой

флуктуационную часть поля течения. Оценка (2.48), с другой стороны,

означает, что, если

c

.1∝c

2

ˆ

/ uL

1

21

)/(

−

xddU

1

∝

c , завихренность крупномасштабных вихрей −

величина того же порядка, что и завихренность среднего течения, и что

соответствующие скорости деформации также сравнимы по порядку

величины.

Оценка рейнольдсового напряжения (2.47) с учетом (2.48) записыва-

ется в окончательном виде

,)

ˆ

(

2

1

2121

xd

Ud

Luc ⋅⋅⋅⋅=

ρτ

(2

где нап

.49)

ряжение

21

τ

и градиент средней скорости относятся к

в (2.4

н

1

21

/ xddU

одной и той же точке пространства. Коэффициент

9) величина

порядка единицы. Выражение (2.49) может быть обобщено для неодно-

родных турбулентных течений к виду (2.41) с определением турбулент-

ной вязкости по формуле (2.43). Такое обобщение представляется

вполне разумным по следующей причине. В рассмотренном выше

идеализированном течении изменения в направлении течения были

«подавлены» в силу предположения, что средняя скорость

1

U

есть

функция только поперечной координаты

2

x

. В большинстве тече-

ний имеют место изменения величин в на авлении течения, которые

включают масштабы времени такие, как

1

11

)/(

−

∂∂ xU

, и линейные

масштабы такие, как расстояние

x

в напр ния, отсчиты-

ваемое от некоторого выбранного ачала. Эти параметры часто могут

не приниматься во внимание по той причине, что в большинстве тече-

ний, представляющих, во всяком случае, практический интерес,

./()/(

211

xUxU

1

c

же

пр

1

авлении тече

)

∂

<<∂∂

58

В заключение полезно сравнить вязкие и турбулентные напряжения.

Для этого рассмотрим отношение

,Re

2

1

21

L

T

x

U

≅=

∂

⋅⋅

ν

νρ

τ

(2.50)

где

− турбулентное число Рейнольдса. Для большинства

турбулентных течений число Рейнольдса

велико, и из (2.50) можно

заключить, что турбулентные напряжения много больше вязких напря-

жений. Таким образом, зависимость среднего течения от числа Рей-

нольдса становится существенной в областях течения, в которых ли-

нейные масштабы

и

ν

/)

ˆ

( LueR

L

⋅=

L

eR

L

u

ˆ

/

ν

оказываются величинами одного порядка.

Это имеет место в областях течения, например, примыкающих к твер-

дым границам.

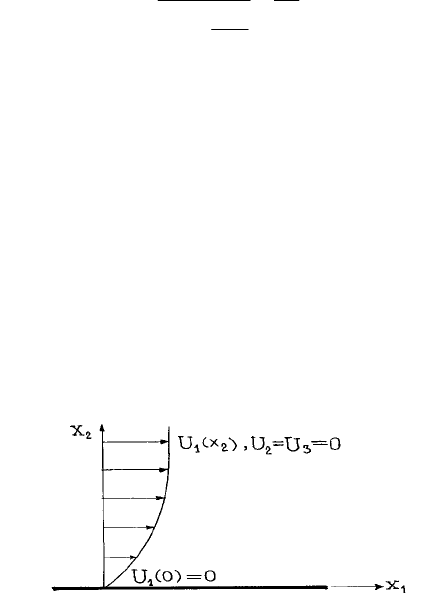
2.3.2. Турбулентный пограничный слой

Плоскопараллельное турбулентное течение над гладкой твердой

поверхностью.

Рассмотрим плоскопараллельный турбулентный поток над

гладкой безграничной поверхностью (рис. 17).

Рис. 17. Турбулентное течение над гладкой твердой поверхностью.

Поверхность расположена в плоскости ( ); скорость

0

2

=x .0)0(

1

=

U

Тече-

ние предполагается установившимся. Средние характеристики потока не

зависят от координаты

в направлении средней скорости течения:

1

x

;0,)(

32211

=

== UUxUU

течение является однородным в плоскости

, градиент давления

),(

31

xx

).3,2,1(0/ ==∂∂ ixP

i

Такое течение можно представить себе как течение, создаваемое в

очень широком канале, верхняя стенка которого движется в своей плоско-

59

сти с некоторой скоростью для поддержания импульса потока, при усло-

вии, что верхняя стенка бесконечно удалена от нижней стенки (

∞

→

2

x

).

Все полупространство

предполагается заполненным турбулентным

течением. Для такого течения уравнение Рейнольдса (2.5) существенно

упрощается:

0

2

>x

,0

1

2

21

2

1

2

=⋅+

xd

d

xd

Ud

τ

ρ

ν

(2.51)

где

−

><−=

2121

uu

ρ

τ

касательное напряжение Рейнольдса. Проинтегри-

ровав один раз уравнение (2.51), найдем

,

21

2

1

2

Const

xd

Ud

=+

τµ

(2.52)

где

−⋅=

ν

ρ

µ

динамическая вязкость.

Постоянная интегрирования определяется из граничного условия на по-

верхности: при

.0,0,0

21212

=

τ

uux Следовательно,

.

00

2

1

2

τµ

=⋅=

=x

xd

Ud

Const

(2.53)

Величина

ρτ

/

0*

=u называется скоростью трения. В результате (2.52)

принимает вид

.

021

2

1

ττµ

=+⋅

xd

dU

(2.54)

Уравнение (2.54) означает, что сумма вязких и турбулентных напряжений

остается величиной постоянной, не зависящей от удаления от стенки.

При малых значениях координаты

, в непосредственной близости от

стенки, турбулентное напряжение

2

x

0

21

≈

τ

. Протяженность этой области

течения, называемой

вязким подслоем, порядка величины

./

*

u

ν

Движение

жидкости здесь обусловлено только вязкими напряжениями, хотя имеются

заметные по величине турбулентные пульсации скорости. По этой причине

движение здесь нельзя считать ламинарным.

Распределение средней скорости в вязком подслое находится из урав-

нения (2.54) при условии, что

0

21

=

τ

:

.)/()(

2021

constxxU +

⋅

=

µ

τ

(2.55)

60

Курбацкий А.Ф. Лекции по турбулентности. Часть 1

Подождите немного. Документ загружается.