Кузнецов В.Г., Куренный Э.Г., Лютый А.П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения

Подождите немного. Документ загружается.

22 Раздел 1

грешности условие выполняется, если коэффициент формы не

превышает 1,11.

Инерционное звено при

γ =

характеризуется функ-

циями: переходной и весовой

{

}

{

}

( ) 1 exp , ( ) exp ,

ht t gt t

−−γ =γ−γ

(1.23)

а также амплитудной и фазочастотной

() , () arctg .

=ϕω=−

+ω

(1.24)

1.5. Осреднение на интервале

В инженерной практике вместо инерционного сглажива-

ния использовалась простейшая оценка по величине и длитель-

ности

θ контролируемого параметра, которая была сформулиро-

вана в виде принципа максимума средней нагрузки

[17]. Напри-

мер, в

[41] в качестве расчетной электрической нагрузки по на-

греву используется получасовой максимум (

θ = 30 мин) средней

нагрузки. Впоследствии этот принцип был распространен на

показатели качества напряжения

[23]. В этом случае вместо

инерционного используется кумулятивное звено 3 (рис. 1.5,а),

которое в темпе реального времени выполняет осреднение

реакции (или помехи) на интервале

θ. Кумулятивный процесс

{

() () ()

yt ytdt L yt

−θ

∫

}

(1.25)

имеет ту же размерность, что и помеха.

Преобразование (1.25) приближенно оценивает энергию

реакции за время кумуляции

θ лишь при небольших различиях в

эффективном и среднем значениях реакции: при выполнении

условия (1.22). Точная оценка энергии дается в рамках модели

Построение моделей электромагнитной совместимости 23

1 3

у у

Рис. 1.5. Блоки осреднения

с квадратором 1 (рис. 1.5,б). Соответствующий квадратичный

кумулятивный процесс

{

}

() ().wt L yt

θθ

= (1.26)

Кумулятивное звено, выполняющее преобразование

(1.25), имеет переходную и весовую функции

/ при 0 , 1/ при 0 ,

() ()

1 при , 0 при ,

ht gt

θθ

≤≤θ θ ≤≤θ

⎧⎧

⎨⎨

≥θ ≥θ

⎩⎩

(1.27)

а также АЧФ и фазочастотную функции

sin( / 2)

( ) sinc( / 2) , ( ) / 2.

θθ

ωθ

ω= = ωθ ϕ ω=−ωθ

ωθ

(1.28)

По аналогии с (1.20) будем использовать приведенный

кумулятивный процесс

() (),

yt wt

θθ

= (1.29)

размерности ординат которого и ординат реакции совпадают.

Кумулятивный процесс отстает от реакции на время

Для ликвидации сдвига интегрирование в (1.25) необходимо

выполнять в пределах от

/2t

−

до , но для этого нужно

знать будущее реакции на интервале

, что предполагает ос-

реднение после записи реакции. В этом случае переходная и ве-

/2t +θ

/2θ

24 Раздел 1

совая функции смещаются влево по оси времени на

– объ-

ект якобы реагирует на единичную функцию за время

до ее

появления, что свидетельствует об искусственности преобразо-

вания. АЧФ от замены пределов интегрирования не изменяется,

а фазочастотная характеристика обращается в нуль. В дальней-

шем будет использоваться интегрирование (1.25) в темпе реаль-

ного времени.

Кумулятивное звено осуществляет непрерывное осредне-

ние на скользящем вдоль оси времени интервале

θ. В [6] исполь-

зуется дискретное осреднение на неперекрывающихся интерва-

лах

θ. В этом случае кумулятивный процесс получается ступен-

чатым. Его можно сгладить по ординатам на концах или на се-

рединах интервалов – при интегрировании от

t – θ до t или от

до .

/2t −θ /2t +θ

1.6. Сопоставление инерционного и кумулятивного

преобразований

Инерционное преобразование отражает физический смысл

моделирования инерционности, в то время как осреднение на

интервале предназначено для других целей. Они разнятся не

только количественно, но и качественно, а потому сопоставле-

ние этих преобразований, строго говоря, не корректно. Однако

осреднение еще используется в директивных документах, в свя-

зи с чем до принятия

физически обоснованных показателей

ЭМС практика требует рассмотрения этого вопроса.

Обычно считается, что кумулятивное преобразование

приближенно моделирует инерционность, если надлежащим

образом выбрать коэффициент пропорциональности

/.T

=θ

(1.30)

Универсального способа определения этого коэффициента

не существует. В

[17] он был принят равным 3 – из условия, что

через время

θ переходные функции кумулятивного и инерцион-

ного звеньев будут отличаться на 5 % (ломаная 1 и кривая 2 на

рис. 1.6).

Построение моделей электромагнитной совместимости 25

, h

Рис. 1.6. Сопоставление переходных функций кумулятив-

ного и инерционного звеньев

Найдем коэффициент пропорциональности по методу

наименьших квадратов за это же время. Для этого необходимо

определить минимум функции интеграла от квадрата разности

переходных функций кумулятивного и инерционного звеньев в

пределах от 0 до

θ. Дифференцируя эту функцию по ε

и при-

равнивая производную к нулю, получим трансцендентное урав-

нение

(

)

{

}

{

}

83 84 12 exp exp ,

θθθθθ

⎡

−ε= +ε+ε +ε −ε ⎤ −ε

⎦

⎣

из которого находим значение 1,63. Соответствующая переход-

ная функция инерционного звена представлена кривой 3.

Если по методу наименьших квадратов аппроксимировать

весовую функцию инерционного звена, то уравнение будет бо-

лее простым:

{

}

(

)

{

}

22expexp

θθθ

−

ε = − ε −ε −ε

решая которое получим значение 1,69, близкое к 1,63.

26 Раздел 1

Величина коэффициента пропорциональности зависит от

длительности интервала, в пределах которого производится ап-

проксимация по методу наименьших квадратов, а также от вида

процесса. Для определенности примем рекомендуемое в

[54]

значение 2,25 (кривая 4), когда

θ = 2,25Т. (1.31)

При отсутствии в реакции периодической составляющей

кумулятивный и инерционный процессы качественно близки,

хотя отличаются количественно. Наличие периодической со-

ставляющей приводит к качественным различиям.

В самом деле, если АЧФ (1.24) инерционного звена моно-

тонно убывает с увеличением частоты (кривая 1, рис. 1.7), то

АЧФ (1.28) кумулятивного звена имеет колебательный характер

(кривая 2). Кривая 1 отвечает физике задачи

: чем больше часто-

та синусоидальной реакции, тем больше инерционность объекта

уменьшает амплитуду синусоидального инерционного процесса

на выходе звена. Напротив, кумулятивное звено для бóльших

частот может дать меньшее ослабление (участки возрастания на

кривой 2), а синусоиды с частотами, кратными

θ , вообще

якобы не воспринимаются объектом.

0,5

4π

, A

Рис. 1.7. АЧФ инерционного и кумулятивного звеньев при

Т = 1 с, ε

= 2,25

Построение моделей электромагнитной совместимости 27

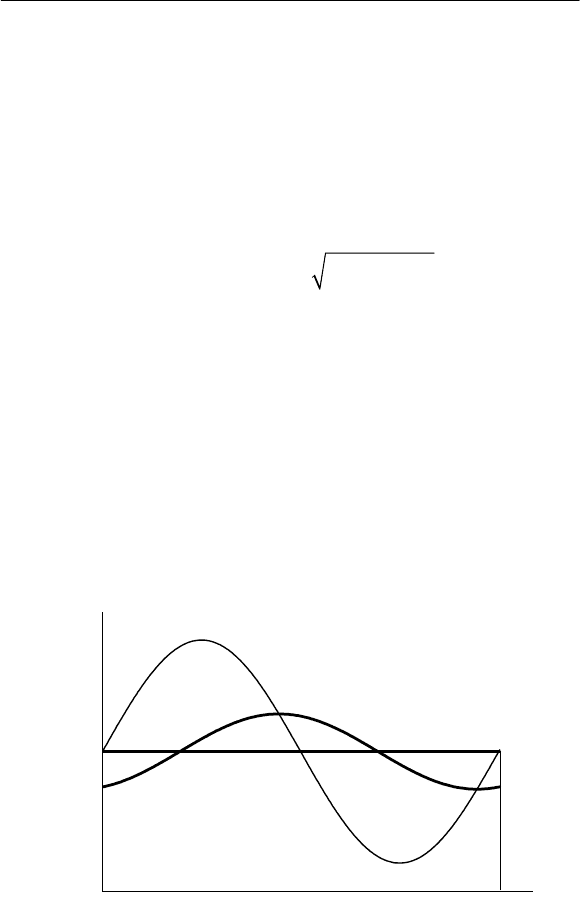
Проиллюстрируем это на следующем примере. Пусть ре-

акция равна сумме постоянной составляющей (среднего значе-

ния)

и синусоиды с амплитудой В, угловой частотой ω

(кри-

вая 1 на рис. 1.8), а длительность кумуляции равна длительности

цикла:

θ = 2π

В стационарном режиме центрированный инерционный

процесс (за вычетом

) представляет собой синусоиду. Подста-

вив в (1.24) значение

Т = θ

, найдем ее амплитуду

()

() /1 2/

BA B

=+πε

и фазу

( ) arctg(2 / ).

ω=− πε

Инерционность объекта приводит к уменьшению ампли-

туды и запаздыванию по фазе. Максимум инерционного процес-

са (кривая 2) превышает среднее значение. Осреднение же дает

противоречащий физике результат: при θ = t

АЧФ (1.28) обра-

щается в нуль, а кумулятивный процесс вырождается в горизон-

таль 3, чем занижается оценка ЭМС.

y, y

, у

Рис. 1.8. Гармонические процессы (θ = t

, ε

= 2,25)

28 Раздел 1

1.7. Показатели ЭМС по тепловым эффектам и потерям

мощности

Несимметрия и несинусоидальность напряжения создают

дополнительные потери ∆Р активной мощности в электропри-

емниках и электрической сети, что приводит к повышению тем-

пературы ϑ. Для обеспечения физического смысла в качестве

показателей ЭМС при решении задач второго типа (п.1.1) есте-

ственно принять характеристики именно этих показателей ре-

жима.

Простейшим дифференциальным уравнением нагрева

электроприемника или проводника с постоянной времени нагре-

ва Т является уравнение первого порядка

+ϑ= I

(1.32)

где I – ток, с

ϑI

– масштабный коэффициент, который связывает

размерности квадрата тока и температуры

. При номинальном

токе I

устанавливается температура, равная длительно допус-

тимой [ϑ]. Отсюда получаем

[

]

=ϑ I

(1.33)

Из сопоставления уравнений (1.18) и (1.32) следует, что

блок КСИ на рис. 1.1 моделирует процесс изменения температу-

ры, если ВФ моделирует проводимость объекта, а реакцией яв-

ляется ток. Физический смысл квадратичного инерционного

процесса состоит в том, что его ординаты пропорциональны

температуре. Выражая ток в процентах от его номинального

значения, принимаемого за 100 %, с учетом

(1.33) получим со-

отношения

[

]

IT I

cw c 10,

−

ϑϑ

ϑ= = ϑ ⋅

(1.34)

Величина ϑ есть превышение температуры объекта относительно

нормируемой температуры окружающей среды.

Построение моделей электромагнитной совместимости 29

в которых температура выражается в °С, масштабный коэффи-

циент – в °С

(%)

В директивных документах помимо длительно допусти-

мой указывается максимально допустимая температура [ϑ

max

]. В

связи с этим одним из показателей ЭМС является максимальная

температура ϑ

max

, которая не должна превосходить нормируе-

мую:

max

≤ [ϑ

max

]. (1.35)

Это условие выражает техническое требование к ЭМС:

если оно нарушается, объект должен быть отключен.

Одной из составляющих ущерба от нарушения ЭМС явля-

ется сокращение срока службы оборудования вследствие уско-

ренного старения изоляции. Тепловые свойства изоляции харак-

теризуются параметром изоляции b, который равен 0,0866 (°С)

–1

для изоляции класса А и 0,0693 (°С)

–1

– класса В.

Тепловой износ определяется средним значением темпе-

ратуры

сс

cw cI

ϑϑ

ϑ= =

которое согласно (1.34) выражается через среднее значение w

квадратичного инерционного процесса или квадрата эффектив-

ного тока I

, не зависящие от постоянной времени нагрева.

Срок службы изоляции уменьшается, если средняя темпе-

ратура превышает длительно допустимую: чем больше разность

∆ϑ

= ϑ

– [ϑ], (1.36)

тем больше сокращается срок службы. Показателем ЭМС явля-

ется кратность снижения срока службы

{

}

exp ,

bγ= ∆ϑ

(1.37)

которая показывает во сколько раз уменьшается срок службы.

30 Раздел 1

Подставив в (1.37) значения параметра изоляции, найдем,

что срок службы сокращается вдвое при повышении температу-

ры на 8°С для изоляции класса А или 10°С – для класса В (вось-

ми- или десятиградусное правила).

Вместо превышения температуры можно использовать

пропорциональные ей разности в (%)

422

сс э э

=10, 10ww I I∆− ∆=−

подставляя их в (1.37) с коэффициентом с

ϑI

Второй составляющей ущерба является стоимость допол-

нительных потерь электроэнергии, которые пропорциональны

среднему значению ∆Р

потерь мощности, а следовательно,

квадрату эффективного тока или величине w

(1.38)

сс

PI PI

PcwcI

∆∆

∆= =

где с

∆РI

– масштабный коэффициент в кВт

(%)

. Величина сред-

них потерь мощности также является физически обоснованным

показателем ЭМС.

1.8. Долевое участие помех

Нагревание объекта происходит под действием полезного

сигнала u(t) и помехи. Если электроприемник недогружен, то

помехи могут и не вызывать превышения температуры. В связи

с этим возникает необходимость в определении доли участия

каждой помехи в нагревании электроприемника, а также оценке

возможности раздельного рассмотрения полезного сигнала и

помех.

Пусть на вход

ВФ подается сумма двух компонент: u(t) и

помехи ν(t), которые имеют средние значения и

и ν

, стандарты

и σ

, а также взаимную КФ k

uν

(τ). ВФ является линейной сис-

темой, поэтому реакция Y(t) фильтра также имеет две компонен-

ты: Y

(t) и Y

(t). Инерционное звено в блоке КСИ осуществляет

линейное преобразование L

, но квадратор делает этот блок не-

Построение моделей электромагнитной совместимости 31

линейным. В результате процесс

[]

{

}

{}{}

{}

() () ()

() () 2 () ()

TTu

Tu T Tu

Wt L Yt Yt

LYt LYt LYtYt

νν

=+=

=++

(1.39)

уже не имеет явного разделения на две компоненты W

(t) и

Tν

(t).

Чтобы найти эти компоненты, надо третье слагаемое раз-

делить между двумя другими

, введя коэффициенты разделения

и ρ

. Тогда

{

}

{

}

{}

() () 2 () () ,

() () 2 () ().

Tu T u u T u

TT Tu

Wt LYt LYtYt

νννν

=+ρ

(1.40)

Покажем, что в общем случае точно так же обстоит дело и

с эффективным значением Y

реакции. Средние значения Y

νc

, стандарты σ

и σ

Yν

компонент, а также момент взаимной

корреляции k

Yuν

между ними определяются по общим формулам

теории вероятностей. С учетом формул для дисперсии суммы

коррелированных процессов получим

()

22 2

ээ сс

Yu Yv Yuv u v

uv Yuvuv

YkY

YY k YY

сс

σ+σ+ + + =

=++ +

(1.41)

где Y

uэ

и Y

vэ

– эффективные значения компонент.

По аналогии с (1.40) запишем выражения для средних

значений компонент

Аналогичная задача возникает при разделении потерь между потре-

бителями

[13].