Кузнецов В.Г., Куренный Э.Г., Лютый А.П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения

Подождите немного. Документ загружается.

52 Раздел 2

ные значения ординат и производных принимаются в качестве

начальных для второго участка, и т.д.

Этот метод «последовательных интервалов» очень удобен

при задании процесса в виде решетчатой функции: дискретной

последовательности ординат. Величина шага дискретизации ∆

настолько мала, что в пределах между смежными ординатами

процесс можно считать неизменным. В результате получается

ступенчатая

функция с одинаковой длительностью ∆ каждой

ступени. Для неизменной функции решение дифференциального

уравнения получить проще.

Для периодических помех можно не рассчитывать пере-

ходный процесс, а сразу получать реакцию в стационарном со-

стоянии.

Во-первых, это можно сделать путем разложения входно-

го процесса в ряд Фурье. В этом случае амплитуда гармоники

умножается на значение АЧФ А(ω) фильтра при частоте гармо-

ники, а к фазе гармоники добавляется значение фазочастотной

функции ВФ при той же частоте. Сумма всех полученных гар-

моник дает периодическую реализацию с той же длительностью

цикла, что и у входного процесса.

Гармоники функционально связаны между собой, но не

коррелированы. Поскольку их среднее значение равно

нулю, то

вне зависимости от фаз гармоник квадраты эффективных значе-

ний

гармоник суммируются:

.YY

∞

µ=

∑

(2.44)

Если для решения задачи достаточно знать эффективное

значение реакции, то любая гармоника или их комбинация мо-

гут рассматриваться раздельно, что является преимуществом

гармонического анализа. Формула (2.44) дает точное решение и

для разрывных функций.

Вместе с тем, при применении рядов Фурье возникают

трудности с выбором количества учитываемых гармоник, осо-

бенно если во

ВФ есть дифференцирующее звено. Кроме того,

ряд точно не воспроизводит используемые в проектировании

Методы расчета показателей электромагнитной совместимости 53

кусочно-линейные и ступенчатые функции в точках их разрыва

– даже при бесконечном количестве гармоник (явление Гиббса).

Во-вторых, реакция может быть получена с использовани-

ем общего решения дифференциального уравнения

п-го поряд-

ка. В этом случае в общем виде записываются выражения для

конечных ординат каждого участка, которые дополняются усло-

виями равенства ординат и

п – 1 производных на границах уча-

стков, а также в начале и конце цикла. Решение полученной сис-

темы алгебраических уравнений позволяет найти неизвестные

ординаты и

п – 1 производные на границах участков.

Перейдем к случайным процессам. Если задан ансамбль

реализаций входного процесса, то каждая из них преобразуется

как детерминированная функция, что дает ансамбль реакций.

При задании характеристик процесса характеристики реакции

могут быть вычислены с использованием переходных или час-

тотных функций ВФ.

В стационарном состоянии среднее значение реакции

(

)

()

сс с

0Yxh xA=∞=

(2.45)

определяется по среднему значению входного процесса.

Корреляционная функция реакции

()

() () ( )

KggK d

∞∞

=ξητ+ξ−ηξ

∫∫

η (2.46)

где ξ и η – переменные интегрирования.

Спектральная плотность реакции

(

)

(

)()

SAS

=ωω

(2.47)

Дисперсия реакции вычисляется по корреляционной

функции при τ = 0 или согласно (1.7) – по спектральной плотно-

сти:

54 Раздел 2

() () ( )

() ()

DggK dd

ASd

∞∞

∞

ξη ξ−ηξη=

=ωωω

∫∫

∫

(2.48)

Использование корреляционной функции требует двойно-

го интегрирования, но она обычно выражается через экспонен-

циальные функции, что упрощает интегрирование. Спектраль-

ная плотность интегрируется один раз, но подынтегральное вы-

ражение оказывается сложным, что требует применения теоре-

мы о вычетах. В связи с этим априори нельзя сказать, какое из

выражений в (2.48) проще.

Взаимные

корреляционные функции между двумя процес-

сами на выходе линейной системы или систем определяются по

формулам, аналогичным (2.46). Если на один и тот же ВФ воз-

действуют два процесса

x(t) и u(t) со взаимной корреляционной

функцией

(τ), то процессы y(t) и ν(t) на выходе ВФ имеют

взаимную корреляционную функцию

()

() () ( )

yxy

KggK d

∞∞

=ξητ+ξ−ηξ

∫∫

(2.49)

Если один и тот же процесс

x(t) поступает на два ВФ с

разными весовыми функциями

(t) и g

(t), то взаимная корре-

ляционная функция между реакциями

(t) и y

(t) составит

()

() () ( )

1,2 1 2

KggKd

∞∞

=ξητ+ξ−ηξ

∫∫

η (2.50)

Взаимные корреляционные функции можно вычислять и

по спектральным плотностям с использованием АЧФ и фазоча-

стотных функций линейных систем (формула (6.10.4) из [50]). В

этом случае интегрирование выполняется один раз, но из-за

сложности подынтегрального выражения такой способ оказыва-

ется трудоемким.

Методы расчета показателей электромагнитной совместимости 55

Определение вероятностного распределения реакции в

общем случае представляет трудную задачу. Исключение со-

ставляет частный случай, когда входной процесс имеет нор-

мальное распределение. Реакция также будет подчиняться нор-

мальному закону распределения с параметрами (2.45) и (2.48).

Известно, что линейные системы нормализируют выходной

процесс – тем больше, чем больше постоянная инерции. Поэто-

му нормальный закон можно

принимать хотя бы в качестве при-

ближения, даже если входной процесс не является нормальным.

2.5. Инерционное сглаживание

Инерционные звенья используются для моделирования

инерционности объектов, а также в методе парциальных реак-

ций. Рассмотрим вначале инерционное сглаживание без квадра-

тора, считая коэффициент передачи

а звена отличным от едини-

цы: в выражении (1.21) в правой его части добавляется множи-

тель

а.

Общее решение дифференциального уравнения имеет вид

()

{} { }

()exp exp ,

yt y a xt tdt t

⎡⎤

+γ γ −γ

⎢

⎣⎦

∫

⎥

(2.51)

где

Тн

– начальная ордината инерционного процесса.

В проектировании входной процесс обычно задан в виде

ступенчатого или кусочно-линейного графика. В первом случае

для

r-ой ступени величиной y

формула (2.51) дает

()

{

}

{

}

(

)

exp 1 exp .

Tr T r r

yt y t ay t

−γ + − −γ (2.52)

Во втором случае на

r-ом участке процесс

(

)

rrr

tctd=+

а инерционный процесс

56 Раздел 2

() ( )

(

)

{

}

exp ,

Tr r r T r r r

yt actT d y acTd t⎡⎤=−++ +− −γ

⎣⎦

(2.53)

где

с и d – параметры прямой.

При квадратичном инерционном сглаживании на вход

звена подается у

(t). Если исходный график является ступенча-

тым, то формула для квадратичного инерционного процесса

()

{

}

{

}

(

exp 1 exp

Tr T r r

wt w t ay t

)

−γ + − −γ

(2.54)

аналогична (2.52). Для кусочно-линейного графика процесс на

каждом участке описывается параболами с коэффициентами

и . В этом случае формула (2.51) дает

()

{}

222

22 2

2exp

Tr r r r r

Tr r r

wayt TtcT abT

wacTd t

⎡

−+ −

⎣

⎤

−− −γ

⎦

(2.55)

График инерционного процесса строится методом после-

довательных интервалов (п. 2.4). Если же входной процесс задан

в виде решетчатой функции, то в пределах каждого шага дис-

кретизации нет необходимости в построении графика инерци-

онного процесса – достаточно вычислять лишь конечные орди-

наты. Для этого в формулы (2.52) и (2.54) достаточно подста-

вить значение t

= ∆. При этом величина

{

}

expb

∆

−γ∆

будет постоянной, а r-ой ординате входного процесса отвечают

ординаты

(

)

()

1 при 1, ..., 1,

Tr T r r

yybay b

wwbay b r N

∆∆

=+−

+− = −

(2.56)

где N – количество ординат входного процесса.

Методы расчета показателей электромагнитной совместимости 57

При t = 0 ординаты инерционных процессов равны нулю,

поэтому искомые решетчатые функции представляют собой по-

следовательности 0, …, y

, …, y

TN – 1

или 0, …, w

, …, w

TN – 1

ор-

динат.

Для периодических графиков сразу находится стационар-

ное решение. Поясним технику вычислений на примере двух-

ступенчатого графика с величинами В

, В

и длительностями t

ступеней, считая В

> В

. После квадратора график сохраняет

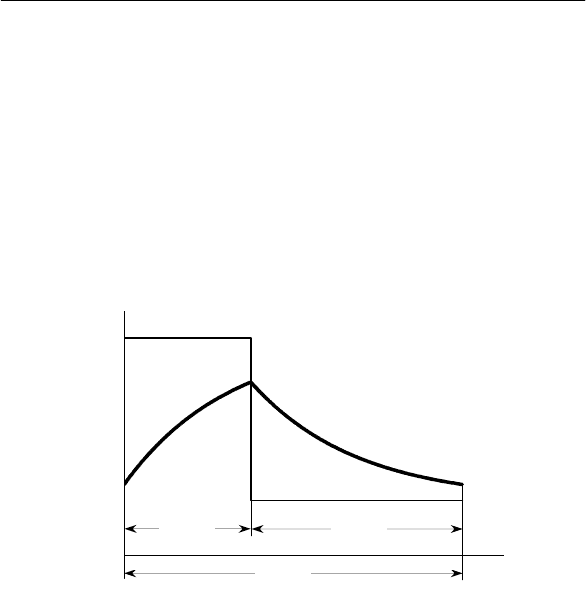
форму, но величины ступеней возводятся в квадрат (рис. 2.4).

Tм

TМ

, w

Рис. 2.4.

Найдем вначале наибольшую w

TМ

и наименьшую w

Tм

ор-

динаты квадратичного инерционного процесса. Для этого со-

гласно (2.54) запишем выражения:

()

{

}

{

}

()

{}

()

{}

м 11

М 1

221ц

exp 1 exp при 0,

exp

1exp при .

wtaB t t

wt w tt

aB t t t t t

⎧

⎡⎤

−

γ+ − −γ ≤≤

⎣⎦

⎪

=−γ−+

⎨

⎪

⎡⎤

+−−γ− ≤≤

⎪

⎣⎦

⎩

(2.57)

Обозначив через

58 Раздел 2

{

}

{

}

1,2 1,2 цц12

exp , expbtbt=−γ =−γ=bb

и подставив в (2.57) абсциссы концов участков, получим фор-

мулы для конечных ординат

(

)

(

)

()

222

к1 м 11 1 111 м

к2222М

TT T

wwbaB baBbaBw

waBbaBw

=+ −=− −

=− −

Сюда добавим граничные условия

Tк1

= w

TМ

, w

Tк2

= w

Tм

Решая систему алгебраических уравнений, получим

()

() ()

222

М 212

222 2 2

м 212 2 2 М 22

waBBB

waBBB baBwaBb

−

⎡⎤

=+−

⎢⎥

−

⎣⎦

−

⎡⎤

=+− =+−

⎢⎥

−

⎣⎦

(2.58)

После определения этих ординат согласно (2.57) строится

график квадратичного инерционного процесса в стационарном

состоянии (рис. 2.4).

Перейдем к случайным процессам. Согласно (2.52) и

(1.24) средние значения инерционных процессов пропорцио-

нальны средним значениям входных процессов:

сс с

(2.59)

где у

и у

– среднее и эффективное значения процесса y(t).

Вычисление корреляционных функций по формулам вида

(2.46) усложнено тем, что корреляционная функция входного

процесса содержит абсолютные значения аргумента, В резуль-

тате приходится различать области, где τ + ξ > η и τ + ξ < η.

Преобразованием осей координат в [12] получены формулы:

Методы расчета показателей электромагнитной совместимости 59

()

{ } () { } ()

{} {}()

exp exp

exp 2 exp ,

Ka Kd Kd

∞τ

∞

⎡

τ= γ −γξ ξ ξ+ γξ ξ ξ+

⎢

⎣

⎤

+γτ −γξξξ

⎥

⎦

∫∫

∫

(2.60)

{}()

exp ,

DY a K d

∞

γ−γξξ

∫

ξ (2.61)

в которых переменная интегрирования положительна. После

интегрирования величина τ заменяется на |τ|.

В случае преобразования (1.21) под K

(τ) и σ

понимаются

корреляционная функция и стандарт реакции ВФ, а под выход-

ным процессом – инерционный процесс. При преобразовании

(1.19) под K

(τ) – корреляционная функция квадрата реакции, а

выходным является квадратичный инерционный процесс. Ко-

нечные формулы для разных входных процессов приведены в

табл. 2.2.

Сглаживающее действие инерционного звена наглядно

проявляется при входном белом шуме: его дисперсия бесконеч-

на, а после инерционного преобразования становится конечной.

Во всех случаях инерционные дисперсии монотонно убывают с

увеличением

постоянной инерции, стремясь к нулю при Т → ∞.

Формулы для входной экспоненциальной функции явля-

ются базовыми для корреляционных функций (1.9) или (1.10),

которые согласно (1.11) представляются в виде двух или четы-

рех экспоненциальных параметров с параметрами

1,2

ω∓

а также стандартами

или

jσ

. Подстановка этих пара-

метров в базовые формулы дает конечные выражения, в кото-

рых мнимые величины отсутствуют.

60 Раздел 2

Таблица 2.2 – Корреляционные функции и дисперсии на

выходе инерционного звена

Вход

Выход

(1.16)

{}

() exp

Yac ac

τ= πγ −γτ

=πγ=π

(1.8)

{} {}

()

{}

222

exp exp при

()

1exp при

⎧

α−ατ−γ−ατ α≠γ

⎪

α−γ

⎪

τ=

⎨

⎪

σ+τ −γτ α=γ

⎪

⎩

=σ =σ

α+γ +α

(1.9)

(

)

{

}

{

()

{}

}

()

2222

222

0000

222

() exp

cos 2 sin exp

Yxa

τ=σ αα+ω−γ −γτ −

⎡⎤

−

γα−ω−γ ωτ+αω ωτ −ατ

⎣⎦

γα+γ

+α

=σ =σ

α+γ +ω +α +ω

(1.10)

(

)

{

}

{

(

)

()

{}

()

222 222

222

000

222

() 2 exp 3

cos sin exp

Yxa

⎡

τ=σ αα+ω −γτ −γ α−ω−γ ⋅

⎣

⎫

⎤

⋅ωτ+ α+ω−γ ωτ −ατ

⎬

⎥

⎦

⎭

γα+γ

+α

=σ =σ

α+γ +ω +α +ω

Обозначение:

()

2222 2

⎡

⎤

γα−ω−γ+αω

⎣

⎦

Методы расчета показателей электромагнитной совместимости 61

При нормальном распределении процесса на входе звена

средние значения (2.59) и дисперсии (табл. 2.2) полностью оп-

ределяют нормальное распределение процессов на выходе зве-

на. При других распределениях решение задачи в конечном виде

может быть получено для небольшого количества частных слу-

чаев.

Например, пусть двухступенчатый график (рис. 2.4) имеет

случайные длительности ступеней, средние значения t

и t

ко-

торых одинаковы, а вероятностные законы распределения явля-

ются показательными:

(

)

(

)

{

}

12ис ис 1,2

exp ,

tft t==λ−λ

где λ

ис

1с 2с

11tt

. Среднее значение t

цc

длительности цикла

равно сумме средних длительностей ступеней, а обратная вели-

чина λ

= λ

ис

/2.

Известно, что для телеграфного сигнала плотность рас-

пределения процесса u(t) на выходе инерционного звена в пре-

делах |u| ≤ 1 дается формулой ([78], (8.50) в [4])

(

)

()

() 1 ,

fu u

λ−

Γλ +

=−

πΓ λ

где λ

– частота перемены знака, Γ(х) – гамма-функция.

В рассматриваемом случае частота перемены знака в два

раза превышает λ

. Сделав подстановку

()

uwaB

=−

−

B−

получим плотность распределения квадратичного инерционного

процесса