Кузнецов В.Г., Куренный Э.Г., Лютый А.П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения

Подождите немного. Документ загружается.

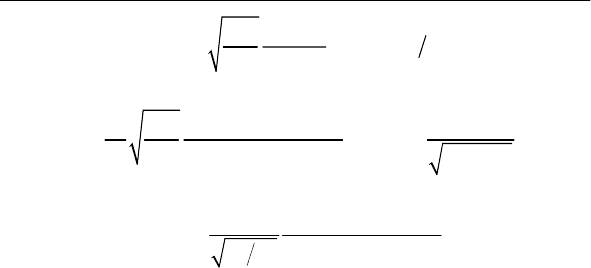
42 Раздел 2

() , 1 ,

Gp T

cTp

π+

=α (2.21)

22 2

00 0

() , ,

TTp

Gp T

TcTp Tp

=σ =

π+α+

+ω

(2.22)

22 2

() .

Tp Tp

=σ

+α +

(2.23)

Формулы (2.3) и (2.4) применяются к составной линейной

системе, передаточная функция которой при m < n равна произ-

ведению (2.1) на G(p). Такая модификация метода применима

только для стационарных состояний, поэтому ее можно назвать

методом стационарных парциальных реакций. Он обеспечивает

полную унификацию расчетов, так как во всех случаях на вход

поступает

только один процесс – белый шум. Несмотря на уве-

личение количества инерционных звеньев, решение упрощается,

так как формулы преобразования белого шума намного проще,

чем для исходных процессов.

При m ≥ n унификация достигается, если переход к со-

ставной системе делает порядок знаменателя ее переходной

функции больше порядка числителя. Так, при т = п

это выпол-

няется для всех выражений (2.21)-(2.23), а при т = п + 1 – толь-

ко для (2.23). Если повышение порядка знаменателя не происхо-

дит, то приходится рассматривать модель с двумя входами: бе-

лый шум подается на составную систему с передаточной функ-

цией, равной произведению первого слагаемого в (2.6) на G(p), а

фактический процесс – на

систему с передаточной функцией

R(p). Однако это усложняет расчеты, поэтому применение мето-

да в таких случаях не всегда целесообразно.

2.3. Преобразование процессов статическими системами

Если помеха задана реализацией, то путем функциональ-

ного преобразования (1.1) находится график реакции, ординаты

Методы расчета показателей электромагнитной совместимости 43

которого возводятся в квадрат, и определяется показатель ЭМС.

Аналитическое решение возможно и для случайной поме-

хи, так как оно сводится к определению законов распределения

реакции y(t) и ее квадрата

() ()zt

по заданному закону рас-

пределения помехи x(t) в пределах ее изменения от х

до х

Статической характеристике (1.1) соответствует обратное

преобразование

х = arc

Если оно однозначное, то плотность распределения реак-

ции определяется по формуле

(

)

(

arc

() arc

)

= y (2.24)

в пределах изменения от у

до у

, которые вычисляются по пре-

делам изменения помехи в зависимости от вида статической ха-

рактеристики: если она возрастает, то

(

)

м,Мм,М

,yx=ϕ если убы-

вает, то

(

)

м,ММ,м

.yx=ϕ

Функция распределения реакции получается либо интег-

рированием выражения (2.24) в пределах от у

до у, либо вычис-

ляется по функции распределения F

(x) помехи: при монотонно

возрастающей статической характеристике

( ) (arc ),

yF y

(2.25)

а при убывающей

() 1 (arc).

yFy

−

(2.26)

При неоднозначной обратной функции возможны два спо-

соба определения распределения реакций. По первому способу

статическая характеристика разбивается на участки монотонно-

го изменения. Для каждого участка по формуле (2.24) вычисля-

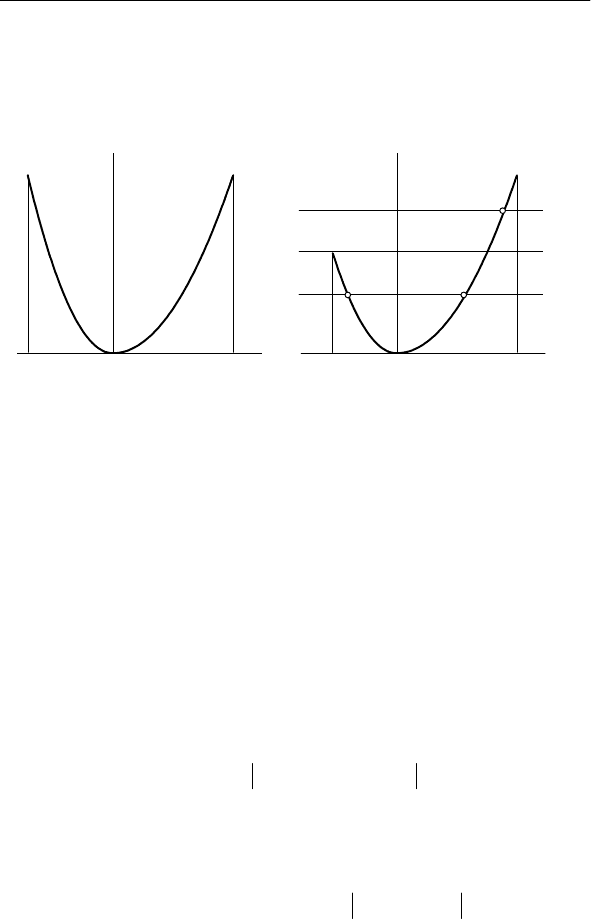
44 Раздел 2

ются составляющие плотности распределения, которые затем

суммируются. Этот способ удобен при неограниченных преде-

лах изменения помехи или при конечных пределах и равенстве

ординат реакции при х

и х

(рис. 2.3,а).

b а

0 0

Рис. 2.3.

По второму способу на графике статической характери-

стики проводятся горизонтали и определяются абсциссы границ

провалов. Функция распределения реакции получается интегри-

рованием функции распределения помехи в пределах провалов.

Например, для случая, когда

arc

по абсолютному значению

меньше

arc

(рис. 2.3,б), получаются две области изменения

реакции, разделенные горизонталью 1. В первой области реак-

ция изменяется от 0 до

arc

. Текущему значению у реакции

отвечает горизонталь 2, которая определяет границы провала

точками а и b с абсциссами

() arc , () arc ,

yyxyy==

являющиеся функциями у. Для этой области

()(

()

() () arc arc .

xx x

)

yfxdxFyFy==−

∫

(2.27)

Методы расчета показателей электромагнитной совместимости 45

Во второй области горизонталь 2 дает пределы интегриро-

вания от

arc

до абсциссы

arc

точки с. Учитывая, что при х ≤ х

функция распределения поме-

хи равна нулю, получим

(

()

arc

() () arc .

)

yfxdxFy==

∫

(2.28)

в пределах от

arc

до

ММ

arc .yx

Плотность распределения реакции получается дифферен-

цированием по у либо конечных выражений в (2.27) и (2.28),

либо интегралов в них – по переменным пределам, без выполне-

ния интегрирования. Наличие двух областей приводит к тому,

что плотность распределения в точке

arcyx=

изменяется

скачком.

Плотность может быть вычислена и с использованием

формулы (2.24). Например, статическая характеристика на рис.

2.3,б разбивается на три участка: от х

до 0 с монотонным убы-

ванием, от 0 до

и от

до х

– с возрастанием. Сумма вы-

ражения (2.24) для первых двух участков дает плотность в пре-

делах от 0 до

arc

, а для третьего участка формула (2.24) оп-

ределяет плотность от

arc

до у

Среднее значение и дисперсия реакции вычисляются по

найденной плотности распределения:

(2.29)

ММ

мм

сс

() , () .

yyfydyDyyfydyy==

∫∫

−

Лишь в некоторых частных случаях эти величины нахо-

дятся по статической характеристике. Следует отметить, что для

нелинейных характеристик у

≠ ϕ

(х

46 Раздел 2

Для линейной статической характеристики

у = ах + b

среднее значение и стандарт

сс

yaxb Dya

+σ==σ

(2.30)

определяются сразу, без предварительного нахождения плотно-

сти распределения.

Подстановка обратной функции

(

)

arc

yyba==−

в (2.24) дает плотность распределения

()

() ,

yfyba

⎡

⎤

=−

⎣

⎦

(2.31)

а в (2.25) и (2.26) – функцию распределения.

Линейная статическая характеристика не меняет вида рас-

пределения. При помехе с нормальным распределением реакция

будет иметь нормальное распределение с параметрами (2.30).

Линейное преобразование помехи с равномерным распределе-

нием в пределах κ

дает равномерное распределение реакции с

параметрами (2.30), диапазоном изменения

23 23

=σ= σ

и пределами изменения у

м,М

= ах

м,М

при а > 0 и ах

М,м

при а < 0.

Независимо от распределения помехи реакция имеет КФ

() ().

KaK

=τ (2.32)

Квадратор в модели ЭМС представляет собой пример не-

Методы расчета показателей электромагнитной совместимости 47

линейной статической характеристики z = y

. Среднее значение

сэ с

=≠

стандарт

эс

yyσ= −

(2.33)

Обратная функция

arcyz==±z

является двузначной. Однако если ординаты реакции только по-

ложительны или только отрицательны, используется одна ветвь

параболы. В этих случаях согласно (2.24) плотность

(

()

)

= z (2.34)

при у ≥ 0 или у ≤ 0. Формулы (2.25) и (2.26) дают функции рас-

пределения

(

)

()

() при 0,

() 1 при 0.

Fz F z y

≥

−− ≤

(2.35)

Рассмотрим знакопеременную реакцию в случае, когда

для z и у выполняются условия, аналогичные для у и х на рис.

2.3,а. Здесь статическая характеристика разбивается на два уча-

стка изменения помехи: от у

до 0 и от 0 до у

. Сумма выраже-

ний (2.24) дает плотность

()()

()

zfzf

⎡

⎤

=−+

⎣

⎦

(2.36)

48 Раздел 2

в пределах от 0 до

. Функция распределения получается

интегрированием выражения (2.36) в пределах от 0 до у. Но ее

можно определить сразу, проведя горизонталь 1 (на рис. 2.3,а не

показана). Тогда согласно (2.27) получим

() (

() () .

yyy

)

zfydyFzFz

−

==−−

∫

(2.37)

При

yy<

и неравенстве ординат на границах измене-

ния реакции (аналогично рис. 2.3,б), необходимо рассмотреть

две области изменения квадрата реакции: от z

= 0 до

и от

до

. Для первой области справедливы формулы (2.36) и

(2.37). Для второго участка

()

() () ,

zfydyFz==

∫

(2.38)

так как для нижнего предела функция распределения реакции

равна нулю. Плотность распределения равна производной по z

от выражения (2.38).

При

yy>

также имеются две области. Для первой из

них справедливы формулы (2.36) и (2.37), но в пределах от 0 до

. Для второй области функция распределения

(

)

() 1

zF=− −z

в пределах от

до

ММ

В случае нормального распределения реакции со средним

значением у

и стандартом σ

квадрат реакции изменяется в бес-

конечных пределах. Подстановка выражений для плотности и

функции распределения реакции (п. 1.3) в (2.36) и (2.37) дает

плотность

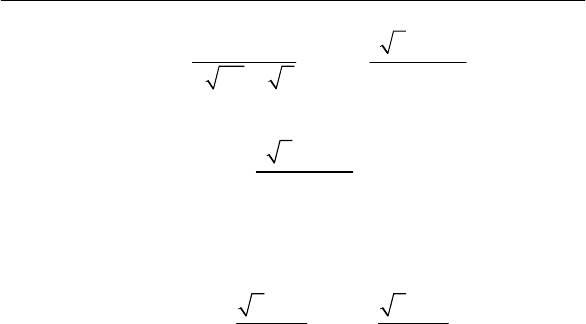
Методы расчета показателей электромагнитной совместимости 49

()

() exp

exp

⎡

⎧

⎫

⎪

−

⎢

−+

⎨

⎬

⎢

πσ

⎪

⎩⎭

⎣

⎤

⎧⎫

⎪⎪

⎥

+−

⎨⎬

⎥

⎪⎪

⎩⎭

⎦

(2.39)

и функцию распределения

() 1,

zy zy

∗∗

⎛⎞⎛⎞

+−

Φ+Φ

⎜⎟⎜⎟

σσ

⎝⎠⎝⎠

−

(2.40)

где учтено соотношение

(

)(

)

∗∗

Φ− =−Φ

Выражения для плотностей и функций распределения

квадрата реакции в случае, когда реакция имеет равномерное

распределение в пределах от у

до у

с диапазоном изменения

, приведены в табл. 2.1.

Как и следовало ожидать, квадратор существенно изменя-

ет вид закона распределения.

В отличие от среднего значения и стандарта, корреляци-

онная функция K

(τ) процесса на выходе квадратора зависит от

вида закона распределения входного процесса. Для ее определе-

ния в общем виде необходимо знать двумерную плотность рас-

пределения ординат входного процесса, разделенных интерва-

лом τ (формула (11.4,б) в [16]). Решение в конечном виде воз-

можно для процесса с нормальным распределением, когда

() 2 () 4 ().

zy y

KKxK

=τ+ τ (2.41)

Спектральная плотность определяется либо по формуле

50 Раздел 2

Таблица 2.1 – Законы распределения квадрата реакции с

равномерной плотностью

Границы

изменения

реакции

Плотность, функция

распределения

, z

)

у ≥ 0

(у

, у

)

(

)

()

() 1 2

()

fz z

Fz z y

=κ

−κ

(

)

мМ

,yy

у ≤ 0

(у

, у

)

(

)

()

() 1 2 при 0

() 1 при

fz z z

zzyzy

κ≥

++ =

−

(

)

Мм

,yy

< 0,

> 0

(

)

() 1 2

()

Fz z y

(

)

0, y

< 0,

> 0

< у

(

)

()

мМ

мм

1 при 0

()

12 при

2 при 0

() при ,

zyz

Fz z y y z y

⎧

κ≤≤

⎪

⎨

κ≤≤

⎪

⎩

⎧

κ≤≤

⎪

=−κ ≤≤

⎨

⎪

⎩

(

)

0, y

< 0,

> 0

> у

(

)

()

Мм

1 при 0

()

12 при

2 при 0

()

1 при

zyz

zy z y

⎧

κ≤≤

⎪

⎨

κ≤≤

⎪

⎩

⎧

κ≤

⎪

⎨

++ =−

⎪

⎩

≤

(

)

0, y

Методы расчета показателей электромагнитной совместимости 51

() () ( ) 4 (),

zyy y

SSSdxS

∞

=ξω−ξξ+ ω

∫

(2.42)

либо интегрированием (2.41) согласно (1.6).

2.4. Преобразование процессов линейными

динамическими системами

В модели ЭМС линейными являются ВФ и инерционное

или кумулятивное звенья. Начальные условия будем считать

нулевыми, что соответствует включению объекта на стационар-

ную помеху. После включения на выходе линейной системы

протекает нестационарный переходный процесс, а затем насту-

пает стационарный режим (теоретически при

t → ∞), для кото-

рого определяются показатели ЭМС. Изложение будем вести на

примере ВФ. Процессы на выходе инерционных звеньев рас-

смотрены в п. 2.5.

Детерминированный входной процесс может быть задан

по-разному. По заданной реализации

x(t) реакция Y(t) находится

либо путем решения дифференциального уравнения, связываю-

щего выходной и входной процессы во ВФ, либо с использова-

нием интеграла Дюамеля:

()() ()()

() ,

Yt ht x d gt x d

′

−ξ ξ ξ= −ξ ξ ξ

∫∫

(2.43)

где

h(t) и g(t) – переходная и весовая функции ВФ, ξ – вспомога-

тельная переменная интегрирования. Реализация реакции начи-

нается с нулевого значения.

Если реализация задана в виде отдельных отрезков, в пре-

делах которых она описывается простыми выражениями, когда

общее решение дифференциального уравнения

п-го порядка из-

вестно, то реакцию удобно находить последовательно. На пер-

вом участке начальные значения ординат и

п – 1 производных

принимаются равными нулю, строится график реакции, конеч-