Кузнецов В.Г., Куренный Э.Г., Лютый А.П. Электромагнитная совместимость. Несимметрия и несинусоидальность напряжения

Подождите немного. Документ загружается.

32 Раздел 1

(

)

()

сэ сс

uu uYuvuv

vv vYuvuv

WY k YY

=+ρ +

(1.42)

Коэффициенты разделения можно принимать из разных

соображений. Как и в [13], это целесообразно сделать по квадра-

там эффективных значений компонент:

222

эс

22 2222

ээ сс

222

эс

22 2222

ээ сс

uuu

uv uvuv

vvv

uv uvuv

YY YY

σ+

ρ= =

+σ+σ++

σ+

ρ= =

+σ+σ++

(1.43)

Таким образом, раздельное рассмотрение компонент не

обеспечивает достоверности оценивания ЭМС. Оно возможно,

если второе слагаемое в выражениях (1.42) будет мало отли-

чаться от нуля. Это условие в общем случае выполняется при

когда ρ

ээ

 1,

}

≈ 1 и ρ

≈ 0, а в частном случае – если пока-

затели ЭМС определяются по средним значениям компонент

квадратичного инерционного процесса, попарно взятые произ-

ведения средних значений компонент и все моменты взаимной

корреляции равны нулю, т.е. когда выражение в скобках обра-

щается в нуль.

Полученные формулы очевидным образом распространя-

ются на любое количество

N помех. В этом случае количество

слагаемых в (1.39) увеличивается:

{} {}

{}{

() () ()

2 () () 2 () () ,

TTu Tr

Tu r T r l

rrl

Wt LYt LY t

LYtYt LYtYt

νν

=≠

=+ +

∑

∑∑

а знаменатель в (1.43) имеет вид

Построение моделей электромагнитной совместимости 33

22222

ээ сс

NNN

ururu

rrr

YY YY

νν

===

+=σ+σ++

∑

∑∑

От r-ой помехи компонента квадратичного инерционного

процесса составляет

{}

() () 2 () ()

() () .

Tr T r r T u r

Tr l

WtLYt LYtYt

LYtYt

ννν ν

νν

≠

⎡

+ρ +

⎢

⎣

⎤

⎥

⎦

∑

(1.44)

В формуле (1.39) компоненты реакции суммируются ал-

гебраически. В общем случае их необходимо рассматривать как

векторные величины, суммируя проекции компонент.

1.9. Нормирование показателей ЭМС

Принцип моделирования распространяется и на задачу

первого типа с тем отличием, что условность норм позволяет

принять некоторые упрощающие допущения. Во-первых, как и в

существующей практике, можно рассматривать помехи раз-

дельно. Тем самым предполагается некоррелированность помех

между собой и полезным сигналом. Во-вторых, поскольку по-

стоянные времени нагрева силового электрооборудования

вели-

ки, оценивание ЭМС достаточно выполнить по эффективному

значению I

νэ

компоненты тока стандартного электроприемника

от помехи, которое не должно превышать допустимое значение:

[

]

ээ

.II

νν

≤

В этом условии ЭМС ток измеряется в процентах по от-

ношению к номинальному току стандартного электроприемни-

ка. Чтобы избежать нормирования этого тока, введем понятие

дозы помехи

34 Раздел 1

ψ = k

, (1.45)

где k

– коэффициент дозы. Физический смысл дозы состоит в

том, что ее квадрат отражает дополнительные потери мощности

в стандартном электроприемнике, а следовательно, средний пе-

регрев и сокращение срока службы.

По аналогии с дозой фликера [58] коэффициент дозы вы-

берем таким образом, чтобы допустимое значение [ψ] дозы бы-

ло равно единице. Допустимое

значение [I

νэ

] компоненты тока

от помехи обычно не известно – нормируется превышение [∆I]

тока от полезного сигнала и помехи. Принимая за 100 % номи-

нальный ток, получим соотношение

[]

()

100 100 ,II

⎡⎤

+=+∆

⎣⎦

из которого найдем

[]

[] []

()

200 .II

=∆ +∆I

)

(1.46)

Из (1.45) следует, что коэффициент дозы

[]

[] []

(

1/ 1/ 200 .kI I I

ψν

==∆+∆

(1.47)

Понятие дозы удобно тем, что условие ЭМС имеет пре-

дельно простой вид:

ψ ≤ 1. (1.48)

Соотношение (1.45) позволяет выбрать структурную схе-

му модели стандартного электроприемника. Не исключено нор-

мирование не структуры и параметров ВФ, а предельных пере-

ходных или частотных функций – как в [8].

Раздел 2

МЕТОДЫ РАСЧЕТА ПОКАЗАТЕЛЕЙ

ЭЛЕКТРОМАГНИТНОЙ СОВМЕСТИМОСТИ

2.1. Исходные данные

Исходными для расчетов показателей ЭМС являются реа-

лизации (графики) помех или их характеристики. В действую-

щих электроустановках записанные графики учитывают все

особенности конкретной сети, состав электрооборудования, на-

личие внешних помех. В проектировании используются графики

нагрузки источников помех – либо расчетные, либо полученные

опытным путем для аналогичных источников помех.

общем случае сеть, электроприемники и средства улуч-

шения ЭМС представляются схемами замещения с сосредото-

ченными параметрами: комбинацией активных сопротивлений,

индуктивностей и емкостей. Внешние и внутренние помехи

учитываются раздельно. Для внешних помех используется рас-

четная схема, в которой источники помех рассматриваются как

источники ЭДС: как бы ни менялись параметры режима элек-

троприемников и источников внутренних помех, график внеш-

ней помехи остается без изменения.

При нахождении графика внутренней помехи источники

помех считаются источниками тока, нагрузка которых инвари-

антна по отношению к любым изменениям в сети (принцип ин-

вариантности индивидуальных нагрузок [11]). В связи с этим

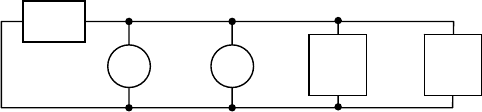
схема замещения (рис. 2.1) представляет собой параллельно со

единенные источника тока i

(t), электроприемники и сеть. По-

мехой является напряжение между точками а и b.

ЭП

Сеть

ЭП

yyy yyy

Рис. 2.1. Расчетная схема для определения внутренней по-

мехи

36 Раздел 2

Для маломощных систем электроснабжения (например,

автономных) источники помех нельзя считать источниками то-

ка, а следует исходить из принципа инвариантности индивиду-

альных проводимостей, которые не зависят от изменений пара-

метров режима сети. В этом случае нагрузки источников помех

будут зависимыми, что усложняет расчеты.

При наличии нескольких источников помех расчеты вы-

полняются по

графикам суммы активных и суммы реактивных

составляющих их токов.

Непериодические помехи обычно задаются в виде решет-

чатой функции: дискретной последовательности ординат с ма-

лым шагом дискретизации ∆ по оси времени. Периодические

помехи могут представляться в виде ряда Фурье.

2.2. Метод парциальных реакций

В моделях ЭМС (рис. 1.1) ВФ обычно являются линейны

ми системами. Процессы в фильтрах описываются линейными

дифференциальными уравнениями, порядок п которых может

быть большим. Нахождение аналитического решения таких

уравнений затруднено как при детерминированных, так и при

случайных помехах.

В таких случаях даже при п = 2 целесообразно использо-

вать метод парциальных реакций, суть которого заключается в

том, что фильтр заменяется эквивалентной

системой, которая

состоит из п параллельно включенных инерционных звеньев

первого порядка [63]. Парциальная реакция каждого звена опре-

деляется очень просто, а искомое решение сводится к суммиро-

ванию парциальных реакций

Задача заключается в нахождении реакции Y(t) на помеху

x(t). В общем виде передаточная функция фильтра пропорцио-

нальна отношению многочленов порядка т и п:

Численное решение задачи можно получить и на компьютере. Одна-

ко для выбора шага дискретизации и в этом случае целесообразно

иметь аналитическое решение – хотя бы в качестве тестовой задачи.

Методы расчета показателей электромагнитной совместимости 37

фф

()

() ,

() 1

mm m m

nn n n

bp b p bp

Wp a a

Np cp c p cp

−−

−

−−

−

++ +

…

(2.1)

где а

– коэффициент передачи фильтра, р – оператор диффе-

ренцирования, b и с – постоянные времени.

Если



– полюса знаменателя, то его можно записать в

виде

(2.2)

() ( )( ) ( ).

Np c p p p p p p=− − −

 

…

При

т < n разложение (2.1) на элементарные дроби позво-

ляет найти параметры

l-го инерционного звена: сопрягающую

частоту

γ=−



(2.3)

и коэффициент передачи

()

()()( )

mm m m

nln

bp b p bp

aa pp

cppp pp pp

−−

−

++++

=−

−−−

…





……

)

(2.4)

где выражение

(

−



в числителе и знаменателе сокращается,

а потому неопределенности 0/0 не возникает. Количество звень-

ев равно

п (рис. 2.2,а). Выражения (2.3) и (2.4) могут быть ком-

плексными.

На выходе каждого звена наблюдается парциальная реак-

ция

у(t), а искомая реакция равна их сумме

(2.5)

() ().

Yt y t

∑

Парциальные реакции также могут быть комплексными,

но при суммировании мнимые величины уничтожаются.

При т ≥ n обобщение метода достигается путем пониже-

38 Раздел 2

ния порядка числителя. С этой целью будем делить многочлены

в выражении (2.1) углом [46] до тех пор, пока в числителе не

останется многочлен Q(p) порядка q = п – 1. В этом случае по-

лученный многочлен R(p) будет иметь порядок r = т – п, а вме-

сто (2.1) получим

()

() ().

()

Wp a Rp

(2.6)

Поскольку q < п, к первому слагаемому можно применить

формулы (2.3) и (2.4). Сопрягающие частоты инерционных

звеньев останутся теми же, но коэффициенты передачи будут

другими, а потому другими будут и парциальные реакции.

…

х у

…

х у

R(p)

а б

Рис. 2.2. Преобразованные структурные схемы фильтров:

при т < n (а) и т ≥ n (б)

Из (2.6) следует, что к п инерционным звеньям (рис. 2.2,б)

добавляется линейная система с передаточной функцией R(p),

Методы расчета показателей электромагнитной совместимости 39

на выходе которой протекает реакция z(t). Поэтому вместо (2.5)

реакция фильтра составит

(2.7)

() () ().

Yt y t zt

∑

Наибольший практический интерес представляют частные

случаи с т = п и т = п + 1. В первом из них r = 0, а следователь-

но, второе слагаемое в (2.6) будет постоянной величиной R

Обозначив через f коэффициенты многочлена Q(p) и

dbc=

делением многочленов в (2.1) найдем

0 ф 0

(2.8)

(

)

()

bcd d

ννν

=− − (2.9)

при ν = 1, 2, … , п – 1.

Тогда выражение (2.6) примет вид

()

ф 0 ф 0

() 1 .

fp fp

Wp a d ad

cp p p p p

−−

−

++ +

=− +

−−

…



…

(2.10)

Отсюда следует, что преобразованная схема (рис. 2.2,б)

включает в себя п инерционных звеньев с сопрягающими часто-

тами (2.3) и коэффициентами передачи

()

ф 0

()()

fp fp

aa d pp

cpp p p p

−−

−

++ +

=− −

−−

…





…

(2.11)

а также пропорциональное звено с коэффициентом передачи

(2.8). Реакция этого звена определяется следующим образом

40 Раздел 2

ф 0

() ().zt adxt

(2.12)

Перейдем ко второму случаю, когда r = 1. В отличие от

предыдущего случая, где величина d

была безразмерной, здесь

отношение

имеет размерность времени, поэтому обозна-

чим его через J

. Кроме того, введем обозначения:

(

)

1110,10

mn n

mn n R

db cJc J Jd

−−

=− =

Деление углом многочленов в (2.1) приводит к следую-

щим выражениям:

(

)

0 ф 11

RadJp

+ (2.13)

(

)

(

)

10 1 1

bcdcd d

ννν− ν

=− − − (2.14)

а выражение (2.6) дает

()

(

ф 1 ф 11

() 1 1.

fp fp

Wp a d ad J p

cpp pp

−−

−

++ +

=− + +

−−

…



…

)

(2.15)

Первому слагаемому соответствует система, также со-

стоящая из п инерционных звеньев с сопрягающими частотами

(2.3) и коэффициентами передачи

()

ф 1

()()

fp fp

aa d pp

cppp pp

−−

−

++ +

=− −

−−

…





…

(2.16)

Добавочная система является форсирующим звеном с ко-

эффициентом передачи а

и постоянной времени J

Аналогичным образом структурная схема преобразовыва-

ется и при m > n + 1. В результате получается п инерционных

звеньев, параллельно которым подключается добавочная систе-

Методы расчета показателей электромагнитной совместимости 41

ма в виде последовательно включенных звеньев с дейст-

вительными или комплексными параметрами.

mn−

Переходные функции инерционных звеньев определяются

согласно (1.23), а системы с передаточной функцией R(p) – с

использованием обратного преобразования L

–1

Лапласа.

Для параллельно соединенных звеньев переходная функ-

ция

{}

()

{

() 1 exp ( ) .

ht a t L R p p

−

=−−γ+

∑

}

(2.17)

Весовая функция

(2.18)

{}

{

() () exp ( ).

ll l

gt h t a t L R p

−

′

==γ −γ+

∑

Для частных случаев второе слагаемое в (2.17) и (2.18) оп-

ределяются выражениями

ф 0 ф 0

() 1(), () () при

ht ad t gt ad t m n

=δ =

(2.19)

[

]

[]

ф 11

() 1() (),

() () () при 1,

ht ad t J t

gt ad t J t m n

=+δ

′

δ+ δ =+

(2.20)

где 1(t) – единичная функция.

Рассмотренный метод применим для анализа любых про-

цессов. В тех случаях, когда нет необходимости анализировать

переходный случайный процесс при включении фильтра на ста-

ционарную помеху, можно добиться унификации расчетов ха-

рактеристик парциальных реакций. Для этого используется

представление стационарной помехи как результата воздействия

белого шума ζ(t

) с параметром с на гипотетическую систему,

передаточная функция G(р) которой зависит от вида КФ помехи.

Так, для КФ вида (1.8)-(1.10)