Майсеня Л.И. Математика в примерах и задачах. Часть 3
Подождите немного. Документ загружается.

59
123
123
123
3211,
26,
235.
ddd
ddd
ddd
−+=
−++=−
−−=
Решая последнюю систему каким-либо методом, получим
3
1,
d
=
2
3,
d
=−
1
2.
d
=
Это значит что в базисе
, ,
abc
вектор
d
имеет коор-
динаты:
(2, 3, 1).
d =−
2-й способ. Векторы образуют базис пространства, если они не-
компланарны. Это равносильно тому, что их смешанное произведение
не равно 0, т. е. (в координатной форме)
321
1120.
213
−
−−≠
−
Вычисление последнего определителя показывает, что он не нуле-
вой. Таким образом, векторы
, ,
abc
образуют базис. Найти координа-
ты вектора
d
в этом базисе можно, как в 1-м способе.
Пример 10. Векторы
a
и
b
не коллинеарны. Найти, при каком α
векторы (1)
с ab
λ
=−+
и (21)
dab
λ
=+−
будут коллинеарны.
Решение. Если
||,
cd
то существует такое число
0,
β
≠
что
,
dc
β
= т. е.
(21)(1),
abab
λβλβ
+−=−+ откуда
(
)
(21)(1)(1)0.
abλβλβ
+−−−+=
Векторы
a
и
b
не коллинеарны, поэтому
210,
10.
λβλβ
β
+−+=
+=
Решая эту систему, находим
1
β
=−
и
2110
λλ
+−−=
или
0.
λ
=
Таким образом, при
0
λ
=
,
с ab
=−+
.
dab
=−
Как легко видеть, век-
торы
,
cd
противоположны, т. е.
.
d
с
=−
Задания
I уровень
1.1. Даны векторы
(1,1,0),
a =−
(2,4,1)
b
=−
и
(3,2,1)
c =
в некотором базисе. Найдите координаты векторов:
60
1)
22;
abc
−− 2)
( )
1
;
2
ab
+
3)
2;
abc
−+
4)
( )
1
2.
3
abc
−+
1.2. Найдите прямоугольные декартовы координаты вектора
,
a
если известны углы
,,
ai
α
∧
=
,,
aj
β
∧
=
,
ak
γ
∧
=
и на
:
a
1)
60,
α
=°
45,
β
=°
120,
γ
=°
2;
a
=
2)
120,
α
=°
150,
β
=°
30,
γ
=°
3;
a
=
3)
180,
α
=°
60,
β
=°
135,
γ
=°
4;
a
=
4)
30,
α
=°
90,
β
=°
0,
γ
=°
6.
a
=
1.3. Заданы векторы
1
(1,2,0),
a =−
2
(3,1,1),
a =
3
(1,0,1)
a =
и
123
2.
aaaa
=−+
Найдите:
1)
123
,,;
aaa
2)
1
cos,,
ai
∧
2
cos,,
ak
∧
3
cos,;
aj
∧
3) координаты вектора
;
a
4)
(
)
1
,,
aa
(
)
3
,;
aa
5)
2
cos,;
aa
∧
6)
1
,
a
пр a
2
.
a
пр a
1.4. Найдите значение числа λ, при котором векторы
6
aijk
λ
=−+
и 5
bijk
λ
=+− перпендикулярны.
1.5. Вычислите работу, произведенную силой
(
)
2,4,3
F
=−
при перемещении ее точки приложения из начала в конец вектора
(
)
2, 3, 1.
S
=−
II уровень
2.1. Даны векторы
(1,5,3),
a =
(6,4,2),
b =−−
(0,5,7),
c =−
61
(20,27,35).
d =−− Подберите числа
,,
αβγ
такие, чтобы век-
торы , ,
и
abcd
αβγ образовали замкнутую ломаную.
2.2. Покажите, что векторы
,,
abc
образовывают в про-
странстве базис и найдите координаты вектора
d
в этом базисе:
1)
(2,1,1),
a
=−
),2 ,1 ,1( −=b ),1 ,2 ,3( −=c );1 ,9 ,8( −−=d
2) ,ia = ,jib += ,kjic ++=
(8, 9, 1).
d
=−−
2.3. Найдите вектор ,b коллинеарный вектору
(1,2,2),
a =−−
образующий с вектором j острый угол и имеющий длину
||15.
b =
2.4. Найдите вектор
,
x
образующий со всеми тремя базис-
ными векторами
,,
ijk
равные острые углы, если
23.
x =
2.5. Найдите вектор
,
x
образующий с ортом j угол 60°, с
ортом
k
– угол 120°, если
52.
x =
2.6. Вычислите координаты вектора, длина которого равна 8,
зная, что с вектором j он образует угол 45°, с вектором k –
угол 60°, с вектором i – тупой угол.
2.7. Определите координаты концов отрезка, который точ-
ками C(2, 0, 2) и D(5, –2, 0) разделен на три равные части.
2.8. Вычислите скалярное произведение векторов:
1) )15cos ,15sin2 ,1( °°=a и
(0, sin15, 2cos15);
b
=°°
2)
(cos60, tg30, 1)
a
=°°
и
(sin90, cos30, tg60).
b
=°°°
2.9. Найдите угол между векторами
1)
(1, cos20, sin20)
a
=°−°
и );20cos ,20sin ,1( °°=b
2) )5sin ,5cos ,0( °°=a и ).1 ,0 ,0(=b
62
2.10. Для векторов
(2,1,5)
a =− и
(3,1,1)
b = найдите вектор
,
c
удовлетворяющий условиям
(
)
,0,
ck
=
(
)
,1,
ca
=
(
)
,4.
cb
=
III уровень
3.1. Даны три некомпланарных вектора ,
и .
abc
Вычислите
значения λ, при которых векторы
,
abc
λ
++
,
abc
λ
++
cba λ++
компланарны.
3.2. Даны три вершины A(3, – 4, 7), B(–5, 3, 2) и C(1, 2, –3)
параллелограмма ABCD. Найдите его четвертую вершину D.
3.3. Даны вершины треугольника A(3, –1, 5), B(4, 2, –5) и С(–
4, 0, 3). Найдите длину медианы, проведенной из вершины A.
3.4. Даны вершины A(1, –1, –3), B(2, 1, –2) и C(–5, 2, –6) тре-
угольника ABC. Вычислите длину биссектрисы его внутреннего
угла при вершине A.
3.5. Треугольник задан координатами своих вершин A(3, –2 1),
B(3, 1, 5) и C(4, 0, 3). Вычислите расстояние от начала координат до
точки пересечения медиан этого треугольника.
3.6. В вершинах треугольника A(1, –1, 2), B(0, 4, 2) и C(2, –1, 1)
сосредоточены массы 1, 2, 3 соответственно. Найдите координа-
ты центра масс этой системы.
У к а з а н и е. Из функции известно, что для пары масс m
1
и m
2
,
сосредоточенных в точках A и B, центр находится в точке, делящей от-
резок AB в отношении
12
21
,
lm
lm
λ == где
1
l
и
2
l
– расстояние от соот-
ветствующих точек до их центра.
3.7. Даны два вектора:
(8, 4, 1)
a = и
(2, 2, 1).
b =− Найдите
вектор
,
c
компланарный векторам a и
,
b
перпендикулярный
вектору
,
a
равный ему по длине и образующий с вектором b
тупой угол.
63
3.8. Векторы
, ,
abc
имеют равные длины и образуют по-
парно равные углы. Найдите координаты вектора
,
c
если
(1, 1, 0),
a =
(0, 0, 1).
b =
3.9. Выразите координаты вектора
a
в базисе
,,
ijk
через ко-
ординаты в базисе
,,
ijk
′′′
и наоборот, если
(cos, sin, 0),
i ϕϕ
′
=
(sin, cos, 0),
j ϕϕ
′
=−
(0, 0, 1).
k
′
=−
14.3. Векторное произведение
Векторным произведением
,
ab
двух векторов a и b на-
зывается вектор, удовлетворяющий следующим условиям:
1)
, sin,;
ababab
∧
=⋅⋅
2)
,,
aba
⊥
,;
abb
⊥
3) тройка векторов
, , ,
abab
– правая.
Векторное произведение обозначают также .ba×
Если хотя бы один из векторов a или b нулевой, то
, 0.
ab
=
Геометрический смысл векторного произведения
,
ab
состоит в том, что длина этого вектора численно равна площади
параллелограмма, который построен на векторах a и b , приве-
денных к общему началу,
,.
Sab
=
Физический смысл векторного произведения состоит в том,
что момент
M
силы ,F приложенной к точке A относительно
точки O, есть векторное произведение векторов OA и ,F т. е.
,.
MOAF
=
64
Свойства векторного произведения
1.
,,;
abba
=−
2.
,,,;
ababab
λλλ
==
3.
,,,;
abcabac
+=+
4.
,0
ab
=
при
0,
a
≠
0
b
≠
тогда и только тогда, когда
векторы a и b коллинеарны.
Если векторы a и b заданы в ортонормированном базисе и
111
(, , )
axyz
= и
222
(, , z),
bxy= то
122112211221
,()()().
abyzyzixzxzjxyxyk
=−−−+−
Последнюю формулу удобно записать в виде формального
определителя третьего порядка
111
222
,.
ijk
abxyz
xyz
=
Пример 1. Пусть
2,
a
=
5,
b
=
,30.
ab
∧
=°
Найти:
1)
,;
ab
2)
,;
abab
+−
3)
2,3.
abab
+−
Решение. 1) По определению векторного произведения векторов
a
и
b
его длина
, sin,25sin305.
ababab
∧
=⋅⋅=⋅⋅°=
2) Используя алгебраические свойства векторного произведения,
имеем:
,,,,,0,,0
2,2,.
ababaaabbabbabab
abba
+−=−+−=−−−=
=−=
Значит,
,2sin,225sin3010.
ababbaba
∧
+−=⋅⋅⋅=⋅⋅⋅°=
3) Используя свойства векторного произведения и условие задачи,
получим:
65
2,32,6,,3, 7, 7535.
ababaaabbabbba
+−=−+−==⋅=
Пример 2. Упростить выражение:
1)
,,,;
ijkjikkijk
+−++++
2)
(
)
(
)
(
)
2,,3,,4,,.
ijkiikkij
++
Решение. Воспользуемся равенствами
,,
ijk
=
,,
jki
=
,,
kij
=
,,
jik
=−
,,
kji
=−
,.
ikj
=−
Тогда имеем:
1) ,,,,,,,
ijkjikkijkijikjijk
+−++++=+−−+
(
)
,,,0222.
kikjkkkikijikiki
+++=−+−+−+=−=−
2)
(
)
(
)
(
)
(
)
(
)
(
)
2,,3,,4,,2,3,4,
ijkiikkijiijjkk
++=+−+=
222
222
2342342343.
ijkijk
=−+=−+=−+=
Пример 3. Вычислить площадь параллелограмма, диагоналями ко-
торого служат векторы 2
pq
+
и
43,
pq
− где
1,
pq
==
,.
6
pq
π
∧
=
Решение. Используем известную из планиметрии формулу площа-
ди параллелограмма и геометрический смысл векторного произведения:
121212
11
sin(,),,
22
пар
Sdddddd
∧
=⋅=
где
1
2,
dpq
=+
2
43.
dpq
=−
Тогда по свойствам векторного произведения получим:
12
11
,2,43
22
11
2,42,3,4,3806,4,30
22
111
10,10sin(,)1011sin2,5.
2226
пар
Sddpqpq
pppqqpqqpqqp
qpqpqp
π
∧
==+−=
=−+−=⋅−+−⋅=
=⋅=⋅=⋅⋅⋅⋅=
Пример 4. Вычислить площадь треугольника ABC и его высоту, опу-
щенную из вершины A к стороне BC, если A(1, 1, 1), B(4, 2, –1), C(2, 3, 0).
66
Решение. Используем тот факт, что
,
1
,
2
ABC
ABAC
SS
∆
= где
,
ABAC
S –
площадь параллелограмма, построенного на векторах
AB
и
AC
. Так
как
,
,,
ABAC
SABAC
=
найдем сначала
,.
ABAC
(41, 21, 11)(3, 1, 2);
(21, 31, 01)(1, 2, 1);
AB
AC
=−−−−=−
=−−−=−
Вычисляем векторное произведение в координатной форме:
( )
123231
,312353,1,5.
211112
121
ijk
ABACijkijk
−−
=−=−+=++=
−−
−
Тогда
222
, 31535.
ABAC
=++=
Значит,
1
35.
2
ABC
S
∆
=
Для нахождения высоты h треугольника ABC воспользуемся фор-
мулой
1
.
2
ABC
Sah
∆
= Тогда
2
,
ABC
S
h
a
∆
= здесь
.
aBC
=
Значит
222
2
353535210
.
6
4116
(24)(32)(0(1))
ABC
S
h
BC
∆
=====
++
−+−+−−
Пример 5. Даны три силы:
1
(2,1,3),
F
=−−
2
(3,2,1),
F
=−
3
(4,1,3),
F =− приложенные к точке A(–1, 4, 2). Определить величину
и направляющие косинусы момента равнодействующей этих сил отно-
сительно точки O(2, 3, –1).
Решение. Пусть сила
F
– равнодействующая сил
123
,,.
FFF
То-
гда
123
(234, 121, 313)(1, 2, 1).
FFFF
=++=+−−++−−+=−
Значит
момент
M
этой силы равен
( )
133331
,313
211112
121
777, 0, 7.
ijk
MOAFijk
ik
−−
==−=−+=
−−
−
=−−=−−

67
Вычисляем
22
||(7)(7)72.
M =−+−= Для нахождения направ-
ляющих косинусов используем формулы (14.9):
71
cos,;
722
Mi
∧
=−=−
0
cos,0;
72
Mj
∧
==
71
cos,.
722
Mk
∧
=−=−
Задания
I уровень
1.1. Даны векторы
a
и
b
такие, что
2,
a
=
3,
b
=
,.
3
ab
π
∧
=
Вычислите:
1)
,;
ab
2)
23, 5;
abab
−+
3)
,.
aba
+
1.2. Для векторов
32
aijk
=−+
и 2
bijk
=+−
найдите:
1)
,;
ab
2)
,;
abab
+−
3)
2, 3.
abab
−+
1.3. Вычислите площадь параллелограмма, построенного на
векторах
(0,1,1)
a =− и
(1,1,1)
b = .
II уровень
2.1. Докажите, что
, 2, ,
ababab
−+=
и выясните гео-
метрический смысл этого тождества.
2.2. Какому условию должны удовлетворять векторы
a
и
,
b
чтобы векторы
ab
+
и
ab
−
были коллинеарными?
2.3.
4,
a
=
5,
b
=
,.
4
ab
π
∧
=
Вычислите площадь тре-
угольника, построенного на векторах
2
ab
−
и
32.
ab
+
68
2.4.
2,
a
=
5,
b
=
,.
6
ab
π
∧
=
Выразите через векторы a и b
единичный вектор
0
,
c
перпендикулярный векторам
a
и
b
и та-
кой, что:
1) тройка векторов
(
)
0
,,
abc
– правая;
2) тройка векторов
(
)
0
,,
bca
– левая.
2.5. Вычислите площадь треугольника с вершинами в точках
A(1, 1, 1), B(2, 3, 4), C(3, 4,2).
2.6. Сила
(2, 2, 9)
F = приложена к точке A(4, 2, –3). Вы-
числите величину
M
момента
M
этой силы относительно точ-
ки O(2, 4, 0).
III уровень
3.1. Вычислите длины диагоналей и площадь параллело-
грамма, построенного на векторах
ajk
=−+
и
.
bijk
=++
До-
кажите, что этот параллелограмм является прямоугольником.
3.2. Найдите составляющую вектора
(
)
1, 2, 0,
a =− перпен-
дикулярную плоскости векторов
1
(1, 0, 1)
e = и
2
(1, 1, 1).
e =
3.3. Найдите синус угла между диагоналями параллело-
грамма, построенного на векторах )1 ,1 ,2( −=a и ).1 ,3 ,1( −=b
3.4. Сила
F
приложена к точке B(2, –3, 4) и перпендикуляр-
на оси Ox. Момент
M
этой силы относительно точки A(4, 0, –2)
равен ).6 ,8 ,12( −=M Найдите
||.
F
3.5. Докажите, что для вектора
,,,
abc
который называет-
69
ся двойным векторным произведением, справедливо отношение
(
)
(
)
,,,,.
abcbaccab
=−
3.6. Найдите
,,,,,
abcmnp
−
если
(1,2,2),
a
=−
(2,3,1),
b=−
(2,2,2),
с =−
(1,3,5),
m=−
(1,0,2),
n
=−
(3,2,2).
p =−
У к а з а н и е. Можно воспользоваться формулой из предыдущей
задачи 3.5.
14.4. Смешанное произведение векторов
Смешанным произведением
(
)
,,
abc
трех векторов
,
a
b и c
называется число, определяемое соотношением
(
)
(
)
,,,,.
abcabc
=
Если хотя бы один из векторов ,a ,b c – нулевой, то их
смешанное произведение равно нулю.
Геометрический смысл смешанного произведения векторов
,a ,b c состоит в том, что его абсолютное значение равно объе-
му V параллелепипеда, построенного на векторах ,a ,b ,c приве-
денных к общему началу:
(
)
,,.
Vabc
=
Свойства смешанного произведения
1.
(
)
(
)
(
)
(
)
,,,,,,,,;
acbcbabacabc
===−
2.
(
)
(
)
(
)
,,,,,,;
abcbcacab
==
(
)
(
)
(
)
(
)
,,,,,,,,;
acbcbabacabc
===−
3.
(
)
(
)
(
)
11221122
,,,,,,
aabcabcabc
αααα+=+
, где
12
,;
αα
∈
R
4.
(
)
0,, =cba при
0,
a
≠
0,
b
≠
0
c
≠
тогда и только тогда,
когда ,a ,b c – компланарные векторы;
5. векторы ,a ,b c образуют базис в трехмерном простран-
70
стве при условии
(
)
;0,, ≠cba
6. если
(,,)0,
abc
>
то векторы ,a ,b c образуют правую
тройку; если
(,,)0,
abc
<
– левую.
В случае, когда векторы ,a ,b c заданы в ортонормиро-
ванном базисе координатами
111
(, , ),
axyz
=
222
(, , )
bxyz
= и
333
(, , ),
с xyz
= их смешанное произведение может быть найдено
по формуле
( )
111
222
333
,,.
xyz
abcxyz
xyz
=
(14.11)
Пример 1. Векторы
,
a
,
b
c
образуют правую тройку, взаимно
перпендикулярны и
||1,
a
=
||2,
b
=
||3.
с
=
Вычислить их смешанное
произведение.
Решение. По определению
(
)
(
)
,,,,
abcabc
=
. Вектор
,
ab
обра-
зует с
a
и
b
правую тройку, причем
,,
aba
⊥
,.
abb
⊥
Значит,
,.
abc
↑↑
Кроме того,
, sin,12sin2.
2
ababab
π
∧
=⋅=⋅⋅=
Тогда
( )
,,, cos,,23cos06.
abcabcabc
∧
=⋅=⋅⋅=
Пример 2. Для векторов
(1,3,2),
a =−
(2,2,1)
b =− и
(4,1,1)
с
=−
найти объем параллелепипеда, построенного на векторах
,
a
,
b
,
c
приве-
денных к общему началу, и определить ориентацию этой тройки векторов.
Решение. Используем формулу (4.11) для вычисления смешанного
произведения в координатной форме:
( )
( )
132910
91
,,221230127229.
23
411411
abc
−−
−
=−==−⋅=−+=−
−−
Поскольку получили отрицательное значение, то тройка векторов
,
a
,
b
c
является левой, а объем параллелепипеда равен модулю сме-
шанного произведения, т. е.
71
(
)
,,
,,2929.
abc
Vabc==−=
Пример 3. Доказать, что точки A(1, 2, –1), B(0, 1, 5), C(–1, 2, 1) и
D(2, 1, 3) лежат в одной плоскости.
Решение. Рассмотрим три вектора:
(
)
01, 12, 51(1, 1, 6),
AB =−−+=−−
( )
( )
11, 22, 11(2, 0, 2),
21, 12, 31(1, 1, 4).
AC
AD
=−−−+=−
=−−+=−
Вычисляем их смешанное произведение:
( )
116116
22
,,2022020,
22
114202
ABACAD
−−−−
−
=−=−==
−
−−
Поскольку оно равно нулю, то это значит, что векторы ,,
ABACAD
–
компланарны. Они лежат в одной плоскости, так как имеют общее на-
чало. Таким образом, точки A, B, C и D лежат в одной плоскости.
Пример 4. Вычислить объем тетраэдра OABC, если
34,
OAij
=+
3,
OBjk
=−+
25.
OCjk
=+
Решение. Используем формулу
1
,
6
OABC
пар
VV=
где
пар
V
– объем параллелепипеда, построенного на векторах
,
OA
,
OB
.
OC
Объем параллелепипеда вычисляется через смешанное про-
изведение
|(,,)|.
пар
VOAOBOC=
Поскольку
( )
340
31
,,03133(152)51,
25
025
OAOBOC
−
=−=⋅=⋅−−=−
то
1
518,5.
6
OABC
V =−=
Пример 5. Вершины треугольника расположены в точках A(1, 1, 1),
B(2, 3, 2) и C(4, 2, 5). Найти расстояние от точки D(5, 3, 6) до плоскости
.
ABC
∆
72
Решение. Убедимся, что точка D не лежит в одной плоскости с
точками A, B и C, для чего найдем смешанное произведение векторов
,,
ABACAD
. Если оно будет не нулевым, то тем самым будет доказа-
но, что векторы ,,
ABACAD
не являются компланарными, а значит,
точки A, B, C, D не лежат в одной плоскости.
Так как
(
)
21,31,21(1,2,1),
AB =−−−=
(
)
41,21,51(3,1,5),
AС =−−−=
(
)
51, 31, 61(4, 2, 5),
AD =−−−= то смешанное произведение равно
( )
121507
57
,,31431410.
23
425203
ABACAD
−−
−−
====≠
−−
−−
Значит,
,,
1.
ABACAD
V
=
Поскольку расстояние h от точки D до плоскости
ABC
∆
численно
равно высоте параллелепипеда, опущенной из вершины D на основание,
в котором лежит
,
ABC
∆
то из формулы
,,,ABACADABAC
VSh
=⋅
находим
(
)
,,
,
,,
1
.
,,
ABACAD
ABAC
ABACAD
V
h
S
ABACABAC
===
Найдем
,.
ABAC
Поскольку
,121(81)(43)(16)75(7,1,5),
314
ijk
ABACijkijk
==−−−+−=−−=−−
то
222
, 7(1)(5)7553.
ABAC
=+−+−==
Таким образом,
13
,
15
53
h== т. е. искомое расстояние равно
3
.
15
Пример 6. Доказать, что векторы
,
a
,
b
c
компланарны, если
2,,3,0.
abbcca
++=
.
Решение. Умножим скалярно данное равенство на вектор
:
a
(
)
(
)
(
)
2,,,,3,,0.
aababcaca
++=
Так как
(
)
(
)
,,,,0,
aabaca
==
то
(
)
,,0
abc
=
или векторы
73
,
a
,
b
c
компланарны.
Доказанное можно обобщить на случай, когда задано равенство
,,,0,
abbccaαβγ
++=
где
,,
αβγ
– числа, среди которых, по
крайней мере, есть одно ненулевое.
Задания
I уровень
1.1. Вычислите смешанное произведение векторов:
1)
(,,);
ijk
2)
(,,);
kji
3)
(,,);
jik
4)
(,,).
ijijk
++
1.2. Определите ориентацию тройки векторов:
1)
(,,);
jki
2)
(,,);
ijjkk
+−
3)
(, 2, 2);
ikjki
++ 4)
(2, , 2).
jkiki
−+
1.3. Вычислите смешанное произведение векторов ,a ,b c и
укажите ориентацию тройки векторов ,a ,b :c
1) ,2 kjia ++= ,2 kjib −+= ;468 kjic ++=
2) ,32 kjia ++= ,23 kjib ++= ;32 kjic ++=
3)
(
)
,11 ,12 ,13=a
(
)
,22 ,23 ,24=b
(
)
;33 ,34 ,35=c
4)
(
)
,5 ,3 ,1=a
(
)
,6 ,4 ,2=b
(
)
7 ,9 ,8=c .
II уровень
2.1. Выясните, компланарны ли векторы ,a ,b :c
1) ,2 kjia −+= ,3119 kjib +−= ;242 kjic −+=
2) ,238 kjia +−= ,2 kjb −= ;32 kjic ++=
3)
(
)
,1 ,1 ,2 −−=a
(
)
,1 ,4 ,4 −=b
(
)
;2 ,6 ,4 −=c
4)
(
)
,1 ,1 ,1=a
(
)
,1 ,0 ,1=b
(
)
1 ,1 ,0=c .
2.2. Установите, образуют ли векторы ,a ,b c базис, если:
1)
(
)
,1 ,3 ,2 −=a
(
)
,3 ,1 ,1 −=b
(
)
;11 ,9 ,1 −=c
2)
(
)
,2 ,1 ,3 −=a
(
)
,2 ,1 ,2=b
(
)
2 ,1 ,3 −−=c .
74
2.3. Вычислите объем параллелепипеда, построенного на
векторах ,a ,b :c
1)
(
)
1, 1, 2,
a =−
(
)
,0 ,2 ,3=b
(
)
1, 1, 1;
c =−
2)
(
)
,1 ,0 ,1=a
(
)
,1 ,2 ,0 −=b
(
)
1, 3, 0.
c =
III уровень
3.1. Вычислите объем тетраэдра с вершинами в точках
A(1, 1, 1), B(2, 3, 2), C(4, 2, 5) и D(5, 3, 6) и высоту, опущенную на
грань ABC из вершины D.
3.2. Векторы a и b образуют угол 30°, ,6=a .3=b Век-
тор c перпендикулярен векторам a и .b Зная, что ,3=с вы-
числите
(
)
cba ,, .
3.3. Даны два вектора
(
)
2 ,10 ,11=a и
(
)
3 ,0 ,4=b . Найдите еди-
ничный вектор ,с перпендикулярный векторам a и b и направлен-
ный так, чтобы упорядоченная тройка векторов ,a ,b c была правой.
3.4. Упростите:
1)
(
)
babca ++ , , ; 2)
(
)
cbacbaba −+−−− 2 , , ;
3)
(
)
accbba +++ , , ; 4)
(
)
cbacba 2 , , ++− .
3.5. Для тетраэдра SABC, заданного вершинами S(1, 0, –1),
A(1, 2, 1), B(–1, 1, 5) и C(–2, 0, 1), найдите:
1) угол между ребрами SA и
,SB
SA и ;BC
2) площадь основания ABC;
3) высоту тетраэдра (из вершины S).
14.5. Цилиндрическая и сферическая
системы координат

75
Цилиндрические координаты являются обобщением поляр-
ных на случай трехмерного пространства.
Рассматривается координатная плоскость xOy с полюсом O
и полярной осью Ox. Пусть M – произвольная точка пространст-
ва, а M
1
– ее проекция на плоскость xOy. Цилиндрическими ко-
ординатами точки M называются три числа
,,,
z
ρϕ
где
,
ρϕ
–
полярные координаты точки M
1
,
1Oz
z
пр MM
= (рис. 14.4),
0,
ρ
≥
[0,2)
ϕπ
∈
или
(,],
ϕππ
∈−
.
z
∈
R
Рис. 14.4
Прямоугольные координаты x, y, z точки M будут связаны с
цилиндрическими формулами:
cos,
sin,
.
x
y
zz
ρϕ
ρϕ
=
=
=
(14.12)
Сферическими координатами точки M называются три числа
,,,
ρϕθ
где
,
rOM
=
ϕ
– полярный угол точки M
1
, а ,
OzOM
θ
∧
=
(рис. 14.5),
0,
r
≥
[0,2)
ϕπ
∈
или
(,],
ϕππ
∈−
[0,].
Θ
π
∈
x
y
z
0
M
1
φ
ρ
M
(
ρ
,
φ
,
z
)
p
76
Рис. 14.5
Прямоугольные координаты точки M связывают со сфери-
ческими формулами:
sincos,
sinsin,
cos.
xr
yr
zr
θϕ
θϕ
θ
=
=
=
(14.13)
Пример 1. Найти цилиндрические координаты по их прямоуголь-
ным координатам, если
(
)
3,1,2,
A −
(
)
1,0,3,
B −
cos,sin,3,
44
Ñ
ππ
−−
77
sin,cos,5.
88
D
ππ
−
Решение. Используем рис. 14.4. Исходя из определения цилинд-
рических координат, имеем:
22
,
xy
ρ =+
cos,
x
ϕ
ρ
=
sin.
y
ϕ
ρ
=
Точка
(3,1,2)
A имеет координаты
3,
x =
1,
y
=
2.
z
=−
Зна-
чит,
( )
2
222
3142.
xyρ
=+=+==
Для нахождения
ϕ
удобно
использовать
tg
ϕ
с учетом четверти, в которой находится проекция A
1
точки A на плоскость xOy (рис. 14.6), а именно:
1
tg,
3
y
x
ϕ ==
1
A
∈
I четверти, значит,
1
arctg.
6
3
π
ϕ ==
x
y
z
0
M
1
φ
M
(
r
,
φ
,
θ
)
θ
r
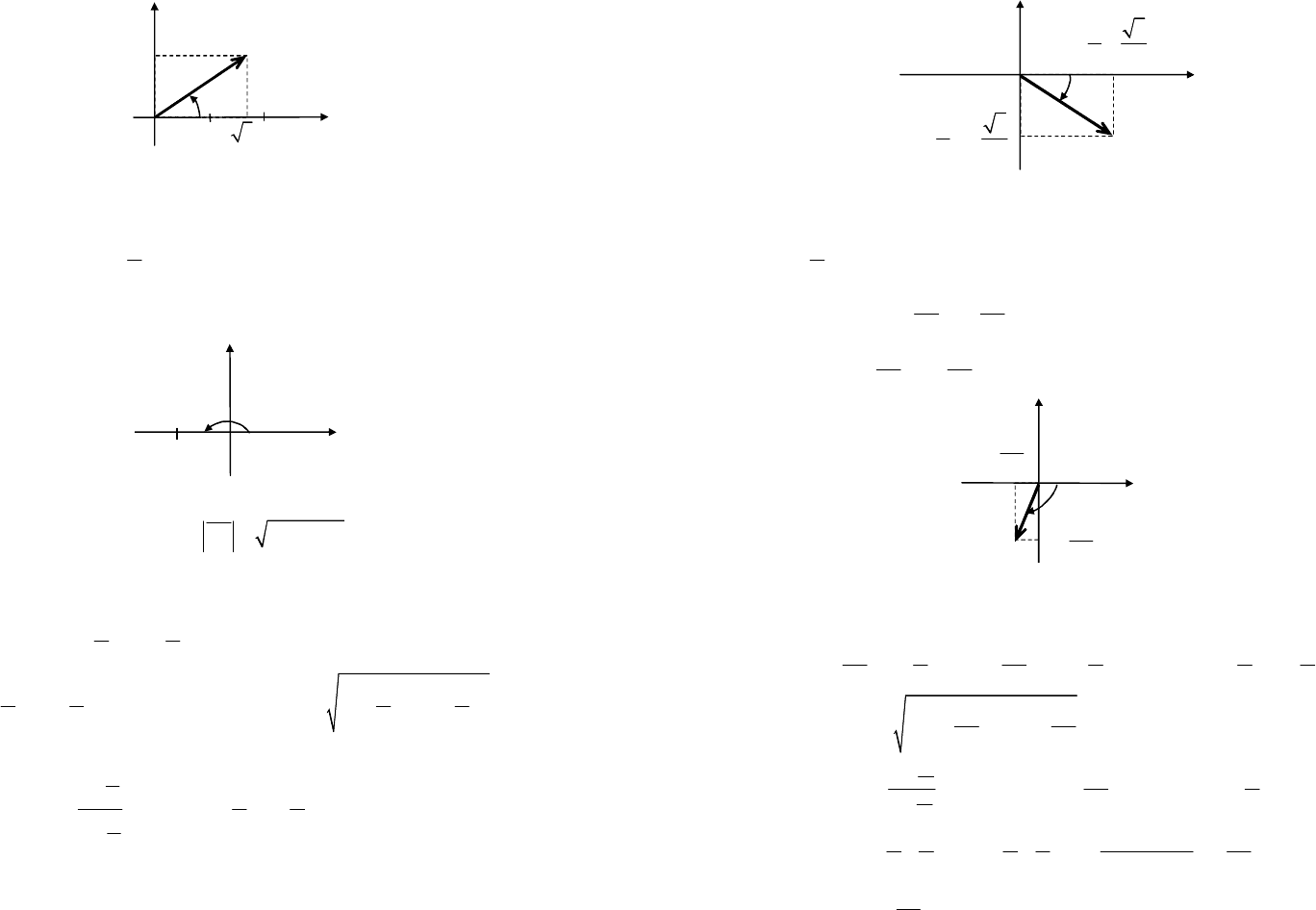
77
Рис. 14.6
Осталось добавить
2.
z
=−
Таким образом, в цилиндрической сис-
теме координат
2, , 2
6
A
π
−
.
Рассмотрим точку
(
)
1, 0, 3
B − . Для наглядности изобразим ее
проекцию B
1
на плоскость xOy (рис. 14.7).
Рис. 14.7
Очевидно, что
(
)
22
1 (1)01,
OBρρ
===−+=
,
ϕπ
=
остается
добавить
3.
z
=
Таким образом, в цилиндрической системе координат
(
)
1, , 3.
B π
Точка
cos,sin,3
44
С
ππ
−−
имеет в плоскости xOy проекцию
1
cos,sin
44
С
ππ
−
(рис. 14.8), для которой
2
2
cossin1.
44
ππ
ρ
=+−=
Находим полярный угол
4
4
sin
arctgarctgtg,
44
cos
π
π
ππ
ϕ
=−=−=−
так как
1
С
находится в IV четверти (рис. 14.8).
0
1
1
2
3
x
y
A
1
ϕ
0
–1
x
y
B
φ
78
Рис. 14.8
Таким образом, в цилиндрической системе координат получаем
1,,3.
4
С
π
−−
Точка
77
sin,cos,5
88
D
ππ
−
имеет проекцией на плоскость xOy
точку
1
77
sin, cos,
88
D
ππ
−
находящуюся в III четверти (рис. 14.9).
Рис. 14.9
Так как
7
sinsin0,
88
ππ
=>
7
coscos0,
88
ππ
=−<
причем
sincos.
88
ππ
<
Для нее
2
2
77
sincos1,
88
ππ
ρ
=−+=
7
8
7
8
cos
7
arctgarctgctgarctgctg
sin88
485
arctgtg.
282888
π
π
ππ
ϕπππ
ππππππππ
ππ
=−−=−−=−=
−−
=−−=−−==−
Итак,
5
15.
8
D, ,
π
−
0
8
7
sin
π
−
x
y
D
1
8
7
cos
π
φ
0
2
sin
42
π
−=−
x
y
С
1
2
cos
42
π
=
ϕ
