Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.

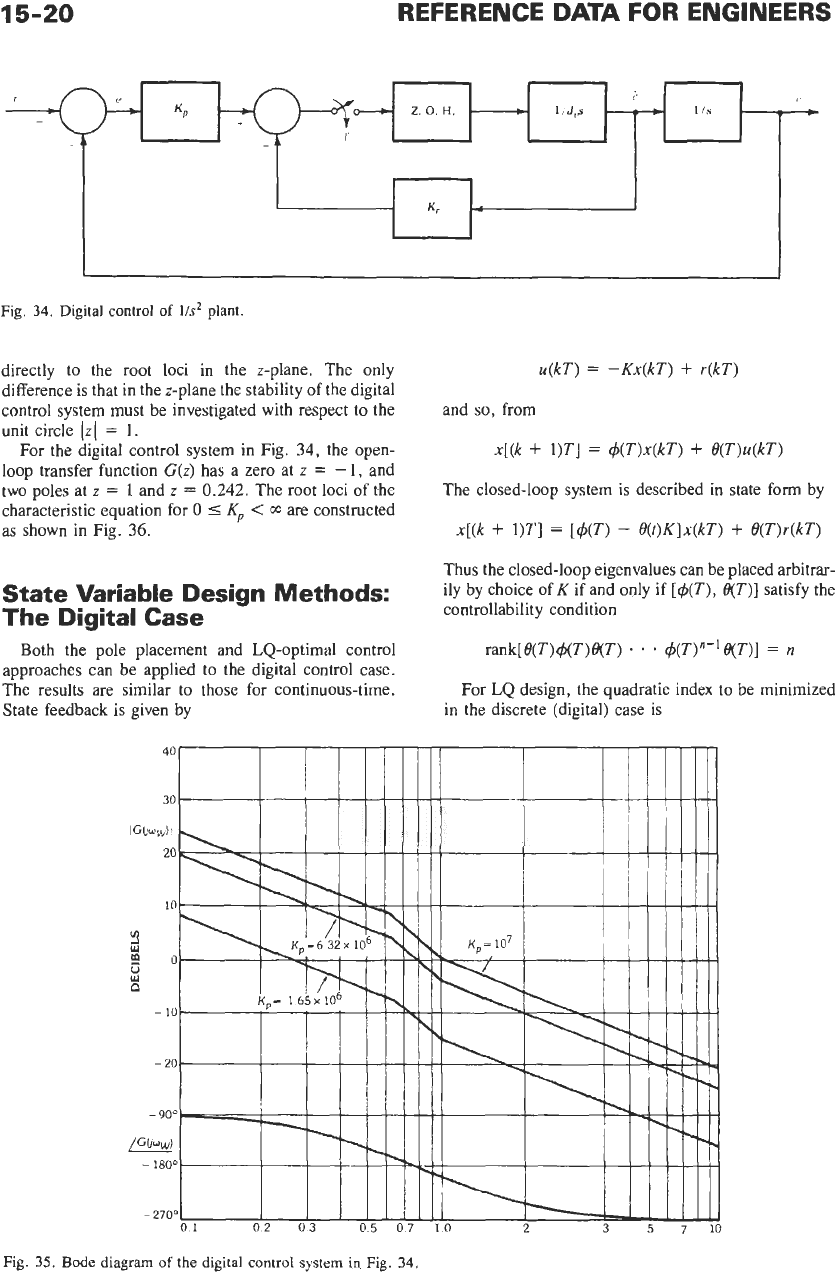
15-20
REFERENCE DATA FOR ENGINEERS
Fig.
34.
Digital control of
Us2
plant.
directly
to
the root loci in the z-plane. The only
difference is that in the z-plane the stability of the digital
control system must be investigated with respect
to
the
u(kT)
=
-Kx(kT)
+
r(kT)
and
so,
from
unit circle
(z(
=
1.
For the digital control system in Fig.
34,
the open-
loop transfer function G(z) has a zero at z
=
-
1,
and
two poles at
z
=
1
and z
=
0.242.
The root loci of the
characteristic equation for
0
5
Kp
<
a
are constructed
as shown in Fig.
36.
State Variable Design Methods:
The Digital Case
Both the pole placement and LQ-optimal control
approaches can be applied to the digital control case.
The results are similar to those for continuous-time.
State feedback
is
given by
x[(k
+
1)TI
=
&T)x(kT)
+
B(T)u(kT)
The closed-loop system is described in state form by
x[(k
+
1)Tl
=
[r$(T)
-
B(t)K]x(kT)
+
B(T)r(kT)
Thus the closed-loop eigenvalues can be placed arbitrar-
ily by choice of
K
if and only if
[4(T),
@T)]
satisfy the
controllability condition
rank[B(T)&T)@T)
*
-
c#(T)"-'@T)]
=
n
For LQ design, the quadratic index to be minimized
in the discrete (digital) case is
Fig.
35.
Bode
diagram
of
the
digital
control
system
in
Fig.
34

FEEDBACK CONTROL SYSTEMS
PHASE
DETECTOR
IhPUT
~
SIGNAL
15-21
FILTER
-
I
PLANE
Kp=1
65x
10'
m
-K,
Fig.
36.
Root
locus
for
C(z)
=
[(1.2
X
lOW7)(2
+
l)Kpl/[(z
-
l)(z
-
0.242)]
30
J
=
2
[x'(kT)Qx(kT)
i-
u'(kT)Ru(kT)],
k=O
where
Q
2
0,
R
2
0.
(Note that, for the digital case, we
require only positive
semidejniteness
for
R,
in contrast
to the positive definite requirement in the analog case).
The optimum control is
u(kT)
=
-
Kx(kT)
where
with
P
being the unique positive definite solution of the
discrete algebraic Riccati equation
(DARE)
P
=
-
PB(0'
P0
+
R)-'OTP]+
+
Q
PHASE-LOCKED LOOP SERVO
SYSTEMS
A
phase-locked loop servo is a closed-loop control
system that
is
used widely in communication systems
for frequency demodulation and bit synchronization.
Phase-locked loop servos are also used for velocity
control, especially when a high degree of speed regula-
tion and accuracy is desired.
A phase-locked loop in its basic form is represented
by the block diagram of Fig.
37.
The input signal and
the feedback signal are sinusoidal, and, upon locking,
both signals will have the same frequency and a
constant phase difference. Any deviation from the
desired phase difference is detected by the phase
detector and is transmitted to the voltage-controlled
oscillator
(VCO)
to correct the error. Since the phase
difference is constant, the frequencies of the input and
the feedback signals are the same. This principle can be
applied to servo systems for which the control objective
is speed regulation.
In the case of a phase-locked loop servo for speed
control, the
VCO
is replaced by an amplifier-motor-
encoder combination. The output of the encoder is a
sinusoidal signal with a frequency proportional to the
angular velocity of the motor. Fig.
38
shows the block
diagram of a phase-locked loop servo.
The main difference between a phase-locked servo
and the conventional servo systems is that the reference
input for a phase-locked servo is a periodic signal rather
than a fixed voltage. The feedback signal from the
encoder is a pulse train whose frequency is proportional
to the speed of the motor. The phase detector compares
the frequencies or phases of the reference and feedback
signals, and generates an error voltage proportional to
the difference. The error voltage is then filtered and sent
to the motor; the motor speed changes to reduce the
--
VOLTAGE-
FEEDBACK
SIGNAL
CONTROLLED
Fig.
37.
Phase-locked
loop.

15-22
REFERENCE
DATA
FOR ENGINEERS
REFEREhCE
DETECTOR AMPLIFIER
FEEDBACK1
I
MOTOR
ENCODER
Fig.
38.
Phase-locked
servo
system
difference between the frequencies or phases of the two
signals. Thus, the motor speed can be synchronized to
the reference frequency.
A typical set
of
signals,
s,(t)
and
sz(t),
is shown in
Fig.
39.
The output of the phase detector,
x(t),
switches
between
0
and
V,
as shown in Fig.
39.
The phase-locked loop servo can be modeled as a
linearized digital control system as shown in Fig.
40.
The loop transfer function of the system in Fig.
40
is
Let
GJs)
=
Km/(l
+
7s)
Then,
%[G,(s)/s]
=
%{Km/[s(l
+
n)]}
=
Kmz/(z
-
1)
-
K,nz/(z
-
Let
K
=
(VxTn/2.rr)Km
Then.
Kz(l
-
e-?")
(z
-
I)(Z
-
e-'")
G(z)
=
The characteristic equation of the digital phase-locked
loop servo is
z2
+
(-1
-
e-T/7
+
K
-
Ke-"7)z
+
e-'/T
=
0
Applying the stability test to the last equation yields the
condition of stability:
K
<
2(1
+
-
NONLINEAR
SYSTEMS
All physical systems have nonlinearities to some
degree. However, there are no general methods of
analysis and synthesis for nonlinear systems. Therefore,
they are often treated with linear approximations, and,
in many cases of small nonlinear effects, satisfactory
results have been obtained. In other cases, however,
linear methods become restrictive in their application
and quite often unrealistic.
There are many approaches to nonlinear systems that
may be applicable
to
a certain type of system but not to
all. Among these methods, two techniques have proved
especially useful. These are the describing function
technique and the phase plane.
The describing-function technique was first applied
to the analysis of nonlinear feedback control systems by
Kochenburger. It is the object
of
the describing-func-
tion method
of
analysis to reduce the representation of
the nonlinearity to an equivalent linear gain and phase
angle. The representation
of
the nonlinearity
is
de-
scribed in terms of the fundamental component of the
distorted output waveform in response to a sinusoidal
input. The result of the describing-function analysis is
an approximate representation of the system in the
frequency domain. The synthesis of nonlinear systems
can be carried out with the describing-function tech-
nique in much the same way as is done with the linear
systems.
The phase-plane method, on the other hand, is a
time-domain representation of the behavior of the first-
and second-order systems portrayed on the phase plane.
The phase-plane diagrams are a useful tool in the study
of transient response to any initial condition and in
some cases to step and ramp inputs. This method can be
extended conceptually to higher-order systems in the
so-called phase space. However, an nth-order system in
the nth-dimensional phase space compared with the
phase plane is difficult to envision and interpret and
may be less effective in its usefulness.
Characteristics
of
Nonlinear
Systems
A comparison of linear and nonlinear systems yields
the following representative characteristics.
X(fJP-
-
y+
$1-
0
f
2T
2T+t2
41
T+1,
Fig.
39.
Typical
input
and output signals
of
the phase
detector.

15-23
w
MOTOR
*
SPEED
x(tJ
GJs)
MOTOR
n/s
ENCODER-COUNTER
Fig.
40.
Linearized model for
a
phase-locked loop servo.
Principle
of
Superposition Does not Apply-In
nonlinear systems, the response to a combination of
individual signals at the input will not be the same as
the response to the sum of those same signals. The
relationship of the impulse response (weighting func-
tion) to the frequency response in linear systems is
therefore not applicable. The familiar Laplace trans-
form operation
(s
=
(T
+
jw)
and the transfer-function
concept used extensively in linear systems cannot be
applied.
Nonlinear Response
is
Dependent
on
Input
Sig-
nal-The response of nonlinear systems is dependent
on the input-signal size and initial conditions as well as
the system parameters.
A
stable response for one input
signal may be unstable for another.
In nonlinear systems, phenomena exist that are not
present in linear systems (generation of new frequen-
cies, jump resonance, limit cycles, etc). The following
are examples of such nonlinear phenomena.
Jump Resonance-The phenomenon called jump
resonance is observed in certain closed-loop systems
with saturation, where the input-output amplitude ratio
and phase angle as a function of frequency exhibit
sudden discontinuities. The typical closed-loop gain
characteristics of a saturating system with jump reso-
nance are shown in Fig.
41.
Amplitude ratio
I
t9,lB,l
is
plotted as a function of frequency for fixed amplitude
8,.
As
the frequency
is
increased from zero, the
frequency response follows the curve along points
A,
B,
and C. At point C a sudden discontinuous jump to
D
is
observed with an incremental increase in frequency.
Further increase in frequency leads to point
E
along the
curve. If the frequency is reversed, the response retraces
the path
E,
D
and continues to point, F, at which a
sudden jump to point
G
occurs; it then continues on
through
B
and A of the gain curve. The phase-angle
response behaves similarly. The overall response curve
exhibits a hysteresis-type property or jump resonance.
Limit Cycle-Limit cycle is an oscillation peculiar
to nonlinear systems. The oscillatory behavior, unex-
plainable in terms of linear theory, is characterized by a
constant amplitude and frequency determined by the
nonlinear properties of the system. Limit cycles are
distinguishable from linear oscillations in that their
amplitude of oscillation is independent of initial condi-
tions. For instance, if a system has a stable limit cycle,
the system will tend to fall into the limit cycle, with the
output approaching the amplitude of that limit cycle
regardless of the initial condition and forcing function.
A
limit cycle is easily recognized in the phase plane as
an isolated closed path as shown in Fig.
42.
Generation
of
New Frequencies-In a nonlinear
system, the output of the nonlinear device contains
harmonic and subharmonic frequencies of the input
signal. For instance, application of two sine waves of
different frequencies
fi
and
fz
to the input will produce
components corresponding to the input frequencies
fi
,
fi,
their sum and difference
fi
k
fz,
their higher
harmonics
mfi
,
nfi
,
and various combinations of sums
and differences
mfi
*
nf2.
In a linear system, only the
components of the input frequencies
fi,
fi
will be
reflected in the output. Clearly, the frequency-response
concept of linear systems must be modified for nonline-
ar applications.
Hysteresis-Multivalued functions exist when two
or more function values correspond to the value of the
variable. Multivalued functions are intrinsically nonlin-
ear. Examples of this are the hysteresis curves of
magnetic materials and the backlash of a gear train.
r:l
2
FREQUENCY
(Ai
Amplitude
ratio
FREQUENCY
(E)
Phose
angle
Fig,
4
1.
Jump
resonance.

15-24
x
eo@)
=
(aoX/2)
+
alX sinwt
+
bl cos
ot
Fig.
42.
Limit
cycle.
Describing-Function Technique
The object of the describing-function technique is to
represent the actual nonlinearity of the system in terms
of an equivalent linear system by considering only the
fundamental component of the output waveform of the
nonlinear element subject to a sinusoidal input. This
technique is valuable in the analysis and design of an
important class of nonlinear feedback control systems,
in which the output of the nonlinear element is acted
upon as it travels around the closed loop by a linear
low-pass filter.
The describing-function analysis is made on the
following basic assumptions.
A.
The input to the nonlinear element
n
is a sinusoi-
dal signal, and only the fundamental component
of the output of
n
contributes to the input. The
output response of a nonlinear element to a
periodic signal consists of the fundamental fre-
quency components of the input signal and its
harmonics. Generally, the harmonic components
are smaller in amplitude compared with the
fundamental component. Further, in most con-
trol systems the system behaves as a low-pass
filter, and the higher harmonics are attenuated. If
the higher harmonics are sufficiently small, they
can be neglected, and the equivalent linear ap-
proximation may be justified.
B.
There is only one nonlinear element in the
system.
All
nonlinearities in the system are
lumped into one single nonlinear element
n.
Fig.
43
shows a block diagram of
a
closed-loop
system containing a nonlinear element
n.
The describing function of a nonlinear element is
defined as the ratio
of
the fundamental-frequency
component of the output as a complex quantity (ampli-
tude and phase angle) to the amplitude of the sinusoidal
input signal. If the input signal as applied to the
nonlinear element
n
is described by
e,(t)
=
Xsinwf
the output response
eo@)
may be expressed by the
Fourier series
The
(ao/2)
term is the dc component;
a,
and
b,
are the
harmonic components.
The fundamental-frequency component of the output
may be expressed in terms of amplitude and phase angle
as
e,l
=
A(w,
X)X sin[ot
+
~$(m,
X)]
In this expression,
A(w,
X)X is the amplitude, and
+(o,
X) is the phase angle of the fundamental compo-
nent. Both amplitude and phase angle are a function of
the frequency and amplitude of the input signal. The
describing function
N(w,
X) by definition is
No,
X)
=
Mw,
X) X exp[Mw, X)l/Xl
=
A(w,
X) exp[.$(w, XI1
=
A(o,
X) cos
&w,
X)
+
jA(w,
X) sin&w, X)
(Eq.
1)
The describing function
N(w,
X) may be purely real
or contain a phase angle depending on the type of
nonlinearity. For single-valued nonlinear functions
N
is
real, whereas for multivalued functions phase shift
exists, generally lagging.
Calculation
of
a
Describing Function-calcula-
tion of the describing function involves performing a
conventional Fourier analysis on the output waveform
to
obtain the fundamental component. The Fourier series
expansion of the output waveform to an input sinusoidal
Xsinot may be expressed as
eo@)
=
(u0X/2)
+
alXsinwt
+
blXcos
wt
+
qXsinwt
+
b,X
COS
2ot
+
'
*
*
For the describing function, only the coefficients of the
fundamental-frequency component are required. The
coefficients may be obtained from the integrals
al
=
(d-' cTfo(t)sinwt.
d(wt)
(Eq.
2)
Fig.
43.
Block diagram
of
nonlinear closed-loop system.

FEEDBACK
CONTROL
SYSTEMS
15-25
bl
=
(rx)-I
rfo(t)
COSOt
'
d(ot)
(Eq.
3)
where
fo(t)
is the exact output of the nonlinear element
expressed as a function of time. The describing function
is then
IN(o, X)l
=
la,
+
jb,I
=
(a:
+
LN(w,
X)
=
tan-'
(b
/a
Where the exact output function &(t) is known, the
above method is applicable. If the function is not
known, a graphical Fourier expansion can be performed
on
the output waveform. Two examples describing the
procedure for calculation of the describing function
using the graphical method are given.
Example
1:
Saturation-Type Nonlinearity-A
nonlinear element with saturation
is
shown in Fig.
44.
Output
y
is held constant for input values greater than
S.
This region is called saturation or limiting. For input
values less than
S,
the output behaves linearly with the
input. The input-output relationship can
be
expressed by
(A)
y
=
kx
for
-S
<x
<
S
(B)
y
=
kS
forx
>
S
(C)
y
=
-kS
forx
<
-S
The output is an odd function, and thus only the sine
term of the fundamental equation need be calculated.
Furthermore, because of symmetry only the first quarter
of the integration need be evaluated as follows:
al
=
(4/rx) rh(t)sinot
. d(ot)
If the input is
x
=
Xsinot, then the outputfo(t)
=
y
is
expressed by
fo(t)
=
kXsinot
X
<
S
and for X greater than
S
fo(t)
=
kX
sinwt
=kS
O
<
ut
<
sin-'(S/X)
sin-'(S/X)
<
wt
<
7~12
Therefore the coefficients
al
are
al=k
X<S
and for X greater than
S
(2k/7i)[4
+
(sin27~)/2]
where
4
=
sin-'(S/X).
The describing function N is given by
N=k X<S
N
=
k(2/7~)[4
+
(sin2+)/2] X
>
S
The variation of amplitude of N with respect to X/S is
plotted in Fig.
45.
The phase angle is zero over the
entire range.
Example
2
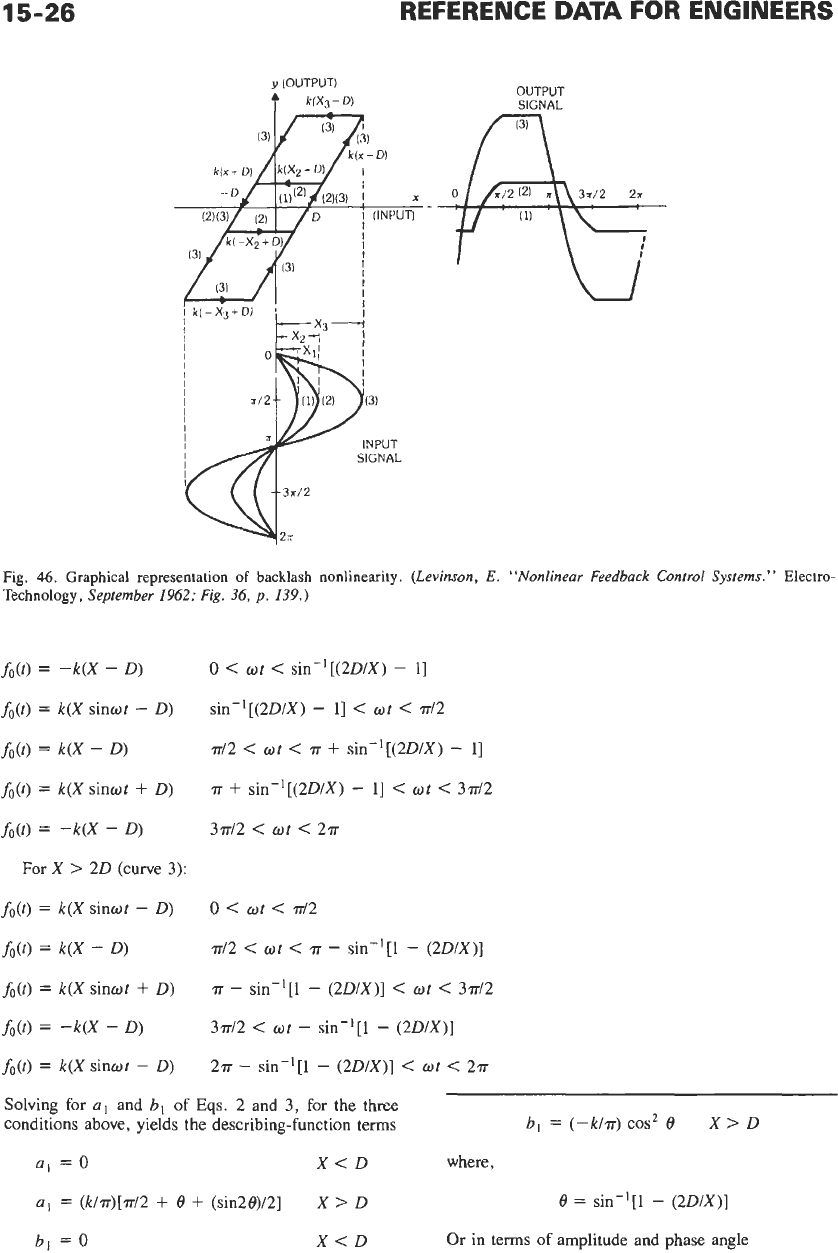
Backlash-Type Nonlinearity-For
the second example, a simple backlash-type nonlineari-
ty (Fig.
46)
is evaluated. The backlash is a multivalued
nonlinearity where the input-output relationship follows
a different path dependent
on
the input-signal amplitude
(curves
1,
2, and
3).
After the steady state is estab-
lished, the outputh(t) corresponding to different values
of X of an input signal
x
=
X sinot are:
For X
<
D
(curve
1):
fact,
=
0
For
D
<
X
<
20
(curve 2):
P
06
I-
'
'0
1
2
3
4
5
6
7
8
9
10
2
02
x/s
Fig.
45.
Describing function for saturation (normalized
amplitude). Fig.
44.
Graphical representation
of
saturation.
15-26
REFERENCE
DATA
FOR ENGINEERS
OUTPUT
Fig.
46.
Graphical representation
of
backlash nonlinearity.
(Levinson,
E.
"Nonlinear Feedback Control Systems."
Electro-
Technology,
September
1962;
Fig.
36,
p.
139.)
fo(t)
=
-k(X
-
D)
fo(t)
=
k(X
sinwt
-
D)
fo(0
=
k(X
-
D)
fo(t)
=
k(X sinwt
+
D)
fo(t)
=
-k(X
-
D)
For
X
>
20
(curve
3):
fo(t)
=
k(X sinwt
-
D)
fo(4
=
k(X
-
D)
fo(t)
=
k(X sinwt
+
D)
fo(r)
=
-k(X
-
D)
fo(t)
=
k(X
sinwt
-
D)
Solving for
al
and
b,
of
Eqs.
2 and
3,
for the three
conditions above, yields the describing-function terms
bl
=
(-k/7j)
cos2
6
X
>
D
al
=
0
X<D
where,
a,
=
(k/.rr)[.rr/2
+
6
+
(sin20)/2]
b,
=
0
X
>
D
X<D
6
=
sin-'[l
-
(ZD/X)]
Or in terms
of
amplitude and phase angle

FEEDBACK CONTROL
SYSTEMS
15-27
The normalized amplitude and phase angle of the
describing function
N
for different values of
D/X
are
plotted in Fig.
47.
The describing function is calculated simply by
determining the fundamental output component of the
nonlinear element. Describing functions for some of the
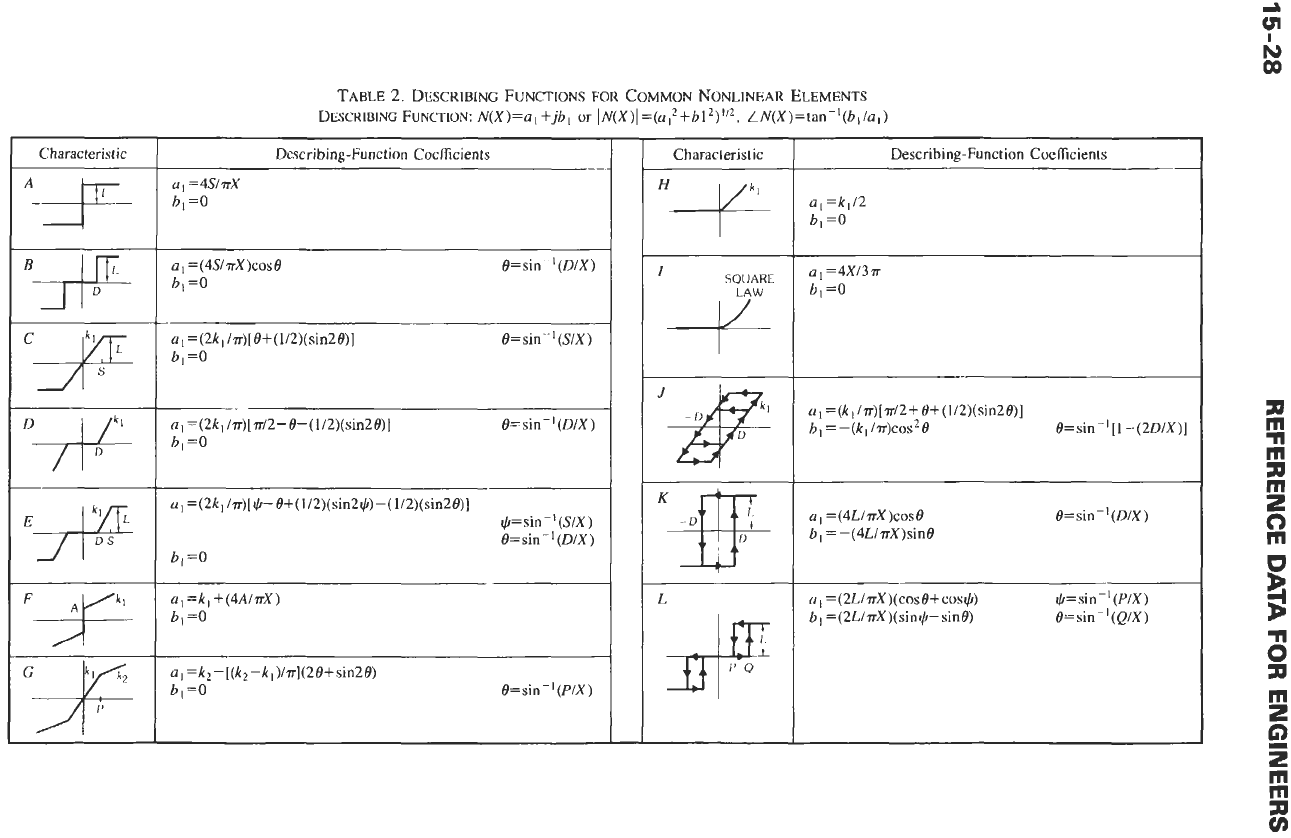
common nonlinear elements are given in Table 2.
Stability Analysis-The describing function
N
of
the nonlinearity can be used to determine the stability
of the system, providing the harmonics are sufficiently
attenuated. In general, the describing function is a
function of both frequency and amplitude of the input
signal.
The closed-loop ‘‘transfer function” of the nonlinear
feedback system in Fig.
48
is given by
The “characteristic equation” of the system is
1
+
N(w,
X)G(jw)
=
0
(Eq.
4)
or
G(jw)
=
-[l/N(w,
X)]
The condition of
Eq.
4
must be satisfied for sustained
oscillation of the output with zero input. Since
N(w,
X)
is a function of both frequency and amplitude, various
combinations of
w
and
X
can be found for oscillation. If
there are no possible combinations satisfying the oscil-
04
5
02
2
‘0
01
02
03
04
05
06
07
08
09
10
11
D/X
Fig.
47.
Describing function
for
backlash (normalized ampli-
tude and phase angle).
Fig. 48. Single-loop nonlinear system.
latory condition, the system is stable. In the case of
sustained oscillation, the oscillatory mode may be either
stable or unstable. If a slight disturbance in amplitude
or frequency occurs and the oscillation returns to its
original value, the oscillation is stable (stable limit
cycle). If the oscillation amplitude increases or decreas-
es from the original value, the oscillation is unstable
(unstable limit cycle). The stability of the closed-loop
system may be evaluated analytically by directly solving
the characteristic equation by any one of the modified
linear graphical methods.
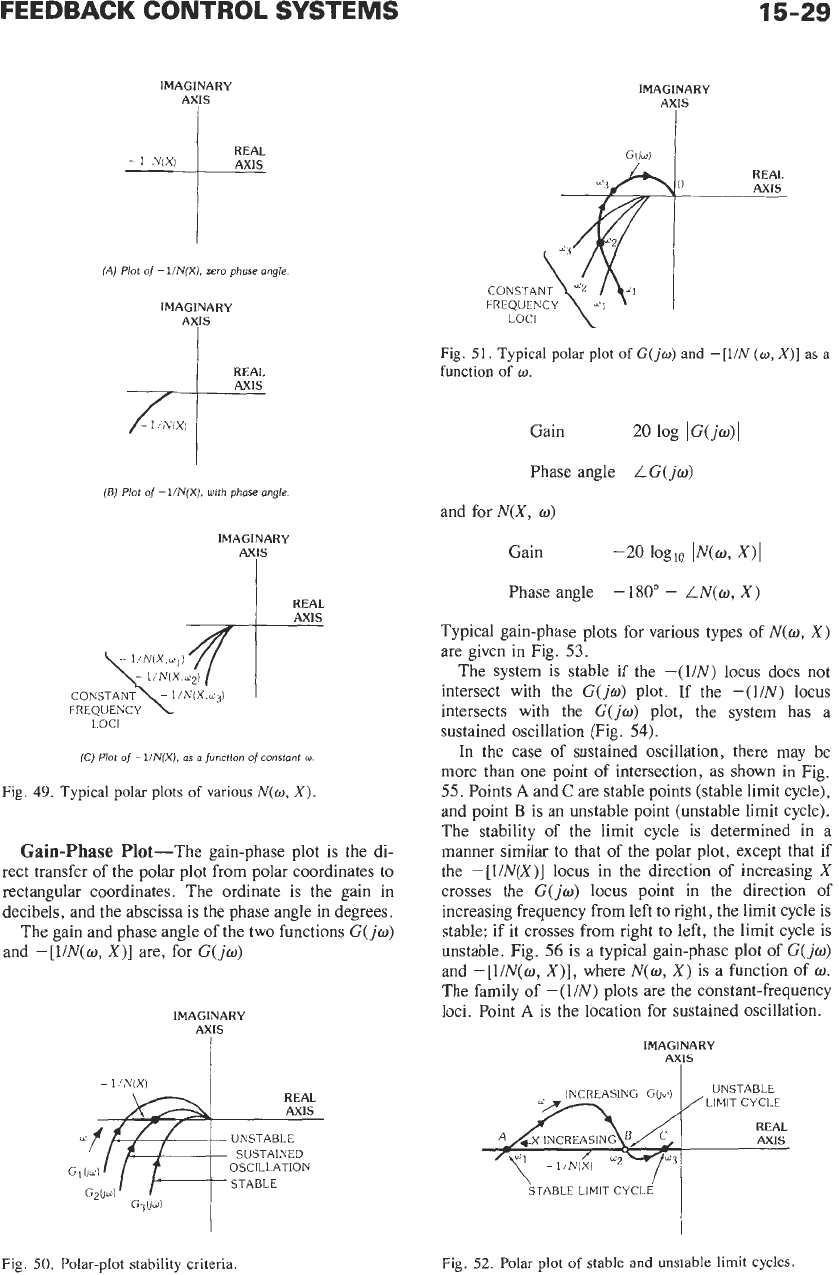
Polar
Plot (Nyquist Diagram)-The conventional
Nyquist diagram must be modified to apply the Nyquist
stability criteria to the frequency-response plot. In a
linear system, the crucial point on the Nyquist diagram
is
-
1.
For nonlinear systems the
-
[l/N(w,
X)]
locus
corresponds to the critical point
-1.
To evaluate the
stability of the system, both
-[l/N(w,
X)]
and the
G(jw)
function are plotted on the polar plane. The
describing function
N(w,
X)
generally is a function of
both wand
X.
If
N
is
only a function of
X,
there will be
one locus
-[I/N(x)]
plotted as a function of
X.
If
N
is
also a function of
w,
a family of constant-frequency loci
are plotted for different values of
w
(see Fig.
49).
The stability of the system is determined by the
following relationship between the
-
[l/N(o,
X)]
locus
and the
G(jw)
plot (Fig. 50). If the
-[l/N(w,
X)]
locus
lies to the left of the
G(jw)
plot or is not enclosed, the
system is
stable.
Conversely, if the
-[l/N(w,
X)]
locus
lies to the right of the
G(jw)
plot or is enclosed, the
system is
unstable.
If the
-
[l/N(o,
X)]
locus intersects
with the
G(jw)
plot, the system may have a
sustained
oscillation.
In the case where
N
is a function of
w,
the
condition for sustained oscillation is satisfied if the
w
of
the G(Jw) plot at the intersecting point is the same
w
of
the
-[UNO,
X)]
locus (see Fig. 51).
The oscillation may be either stable or unstable. If
the
C(jo)
intersects with the
-[l/N(w,
X)]
locus at one
point only, the oscillation is stable (stable limit cycle).
If more points of intersection exist, the limit cycle may
be either stable or unstable. The stability of the limit
cycle is determined by the direction
of
the two loci at
the crossover point.
By establishing the
G(jw)
locus pointing in the
direction of increasing frequency
as
a
reference, if the
-[l/N(X)]
locus pointing in the direction of increasing
amplitude
X
crosses the
G(jw)
locus from right to left,
the limit cycle is stable. If the crossover occurs from left
to right, the limit cycle is unstable.
A
polar plot with
both stable and unstable limit cycles is shown in Fig.
52.
I
Characteristic
TABLE
2.
DESCRIBING
FUNCTIONS
FOR
COMMON
NONLINEAR
ELEMENTS
DESCKIBING FUNCTION: N(X)=a
I
+jb
or
IN(X)l
=(u
+
b12)"*. LN(X)=tan-'(b
1
/a
I
)
Describing-Function Coefficients
(I
,
=4s/Trx
b,
=O
a,
=
(2kl
/v)[
e+(
1/2)(sin20)]
bi=O
a,
=(2kl /~)[~/2-O-(1/2)(sin2O)]
bl=O
O=
sin
-
'
(DIX)
ul
=(2kl/~)[+-Ot(1/2)(sin2+)-(1/2)(sin20)]
t,b=
sin
-'
(SLY)
O=sin-l
(DK)
6,
=O
a,
=k2-[(k,-k,)/~](20+sin20)
b,
=O
O=sin-' (f/x)
Characteristic
"+
SQCJARE
I
L
3-F
Describing-Function Coefficients
al=kl/2
b,
=O
a'
=4x/37r
6,
=O
a,
=(k1/~)[~/2+ 8+(1/2)(sin20)]
b
I
=
-(kl
/?r)cos2
0
O=sin-'[l-(2DIX)]
a'
=(4L/TrX)cosO O=sin-' (DIX)
b, =-(4L/~rX)sinO
U'
=(2L/7rX)(cosO+cos+) +=sin
-I
(PIX)
b
I
=
(2L/~rX)(sin+-sinO)
O=
sin-' (QlX)
FEEDBACK CONTROL SYSTEMS
15-29
IMAGINARY
AXIS
IMAGINARY
AXIS
(A)
Plot
of -l/N(X),
zero
phase angle.
IMAGINARY
REAL
T
-
1
,NLy
(5)
Plot
of
-l/N(X),
with
phase
ongle.
IMAGINARY
AXIS
I
i
REAL
(C)
Plot
of-l/N(X),
os
o
function of
constant
o
Fig.
49.
Typical
polar
plots
of
various
N(w,
X).
Gain-Phase Plot-The gain-phase plot is the di-
rect transfer of the polar plot from polar coordinates to
rectangular coordinates. The ordinate
is
the gain in
decibels, and the abscissa is the phase angle in degrees.
The gain and phase angle of the two functions
G(jw)
and
-[I/N(w,
X)]
are, for
G(jw)
IMAGINARY
AXIS
I
UNSTABLE
SUSTAINED
OSCILLATION
STABLE
CONSTANT
Ld2
1
1
FREQUENCY
\I
I"'
I
LOCI
Fig.
51.
Typical polar plot
of
G(jw)
and
-[11N
(a.
X)]
as a
function
of
w.
Phase angle
LG(jw)
and for
N(X,
w)
Gain
-20
log,o
IN(@,
XI1
Phase angle
-180"
-
LN(w,
X)
Typical gain-phase plots for various types of
N(w,
X)
are given in Fig.
53.
The system is stable if the
-(l/N)
locus does not
intersect with the
G(jw)
plot. If the
-(l/N)
locus
intersects with the
G(jo)
plot, the system has a
sustained oscillation (Fig.
54).
In the case of sustained oscillation, there may be
more than one point of intersection, as shown in Fig.
55.
Points
A
and C are stable points (stable limit cycle),
and point
B
is an unstable point (unstable limit cycle).
The stability of the limit cycle is determined in a
manner similar to that of the polar plot, except that if
the
-[l/N(X)J
locus in the direction of increasing
X
crosses the
G(jw)
locus point in the direction of
increasing frequency from left to right, the limit cycle is
stable; if it crosses from right to left, the limit cycle is
unstable. Fig.
56
is a typical gain-phase plot of
G(jw)
and
-[l/N(o,
X)],
where
N(w,
X)
is a function
of
w.
The family of
-(l/N)
plots are the constant-frequency
loci. Point
A
is
the location for sustained oscillation.
IMAGINARY
AXIS
\,TABLE LIMIT CYCLE
:I
Fig.
50.
Polar-plot stability criteria.
Fig. 52. Polar plot
of
stable and unstable limit cycles.
