Миронов С.В., Пищухин А.М. Метасистемный подход в управлении

201

даемых и порождающих переменных. Для удобства обозначений кодирую-

щая функция (В.6) может быть заменена двумя функциями

ggg

KM →:

λ

, (В.12)

ggg

KM →:

λ

,

с помощью которых множества состояний

G

и

G

соответственно порождае-

мых и порождающих переменных задаются декартовыми произведениями

k

Kk

SG

g

∈

×

=

,

k

Kk

SG

g

∈

×= . (В.13)

Теперь способ представления состояния порождаемых переменных (скажем

G

g

∈ ), определяемого по состоянию порождающих переменных (скажем,

G

g

∈

~

), можно выразить функцией

{

}

1,0: →

×

GGf

GB

, (В.14)

где

()

ggf

GB

,=

Назовем эту функцию

порождающей функцией поведения.

Если маску

M

и функцию

B

f из (В.2) заменить соответственно на

G

M

и

GB

f , то получится альтернативная система

),(

,

GB

fGGB

MIF = . (В.15)

Будем называть такую систему

порождающей системой с поведением.

Использование использующей системы с поведением для порождения

данных включает следующие два этапа:

а) для некоторого значения

T

t

∈

задано состояния Gg

~

∈ ; для опреде-

ления состояния

G

g

∈ при том же значении используется функция

GB

f ;

б) значение

t

заменяется на новое и повторяется этап а).

Необходимо прояснить несколько вопросов, связанных с двухэтапной

процедурой порождения. Во-первых, на этапе а) неявно предполагается, что

при заданном значении

t

состояние

g

известно. При первом выполнении

этого этапа данное состояние определяется пользователем как походящее

на-

чальное условие.

Однако после этого все полностью определяется самим про-

цессом порождения, то есть состояниями

g

и

g

, связанными с предшест-

вующим значением

t

. При этом предполагается, что значения

t

должны на

этапе (б) изменяться в соответствии с порядком, заданным на множестве

T

.

Таким образом, значения

t

заменяются или на

1

+

t

, или на

1−

t

. В первом

варианте начальное условие должно быть определено для наименьшего воз-

можного значения

t

, а во-втором – наибольшего возможного значения

t

.

Во-вторых из необходимости порождения данных в одном из двух по-

рядков следует, что существует только два содержательных разбиения маски

на

M

на

g

M и

g

M , каждое из которых соответствует одному из двух поряд-

ков порождения. Если данные порождаются в порядке возрастания (убыва-

0, если

g

не может иметь место или если имеет место

g

1, если

g

может иметь место или если имеет место

g

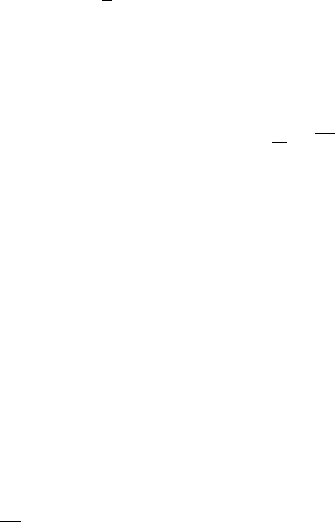
202

ния)

t

, то

g

M содержит ровно по одному элементу каждой подмаски

i

M

)(

n

Ni ∈ , определенной в (В0), элемент с наибольшим (наименьшим) значе-

нием

ρ

; остальные элементы

M

входят в

g

M . Таким образом, графически

получается, что

g

M - это множество самых правых элементов

M

(правый

край этой маски) или, наоборот, множество самых левых элементов

M

(ле-

вый край маски).

В-третьих, предполагается, что для любого состояния

Gg ∈ имеется по

крайней мере одно состояние

G

g

∈

, допустимое функцией

GB

f [то есть

),(

ggf

GB

−

=1]. Если допускается только одно состояние, то для любого на-

чального условия данные порождаются однозначно: такие системы называ-

ются

детерминированными. Если допускается более чем одно состояние, то

порождение данных проблематично, так как порождаемое состояние не все-

гда однозначно определено. Для таких систем выбирающие функции поведе-

ния не подходят. Более содержательно они описываются функциями поведе-

ния других типов, рассматриваемых далее. Для детерминированных систем

представление (В4) порождающей функции поведения

GB

f может быть заме-

нено более простым

.: GGf

GB

→ (В.16)

Пример В.1 Для пояснения процесса порождения данных порождающей

системой с поведением типа, определяемого уравнением (В.15), положим,

что подобная система состоит из упорядоченного параметрического множе-

ства

99

NT = и пяти переменных

51

,...,vv , состояния которых будут определе-

ны ниже. Воспользуемся маской, заданной на рисунке В.2. Данные могут по-

рождаться или в порядке возрастания, или в порядке убывания значений

параметра

t

. Оба эти варианта показаны соответственно на рисунках В.4 и

В.5. В первом случае (рисунок В.3) порождаемые выборочные переменные

– это переменные, соответствующие правому краю маски, то есть

2

s ,

4

s ,

7

s ,

9

s ,

10

s ; остальные выборочные переменные являются порождающими. По-

рождение данных в матрице данных происходит слева направо. Пусть поро-

ждающая функция поведения

GB

f , представленная в виде (В.16), определяет-

ся уравнениями

ttttttk

ssssss

,8,6,5,3,1,

+

= (mod k)

при k=2, 4, 7, 9, 10. Множества состояний порождаемых переменных опреде-

ляются этими уравнениями, а множества состояний порождающих перемен-

ных – их положением в маске. Например, множество состояний порождаемой

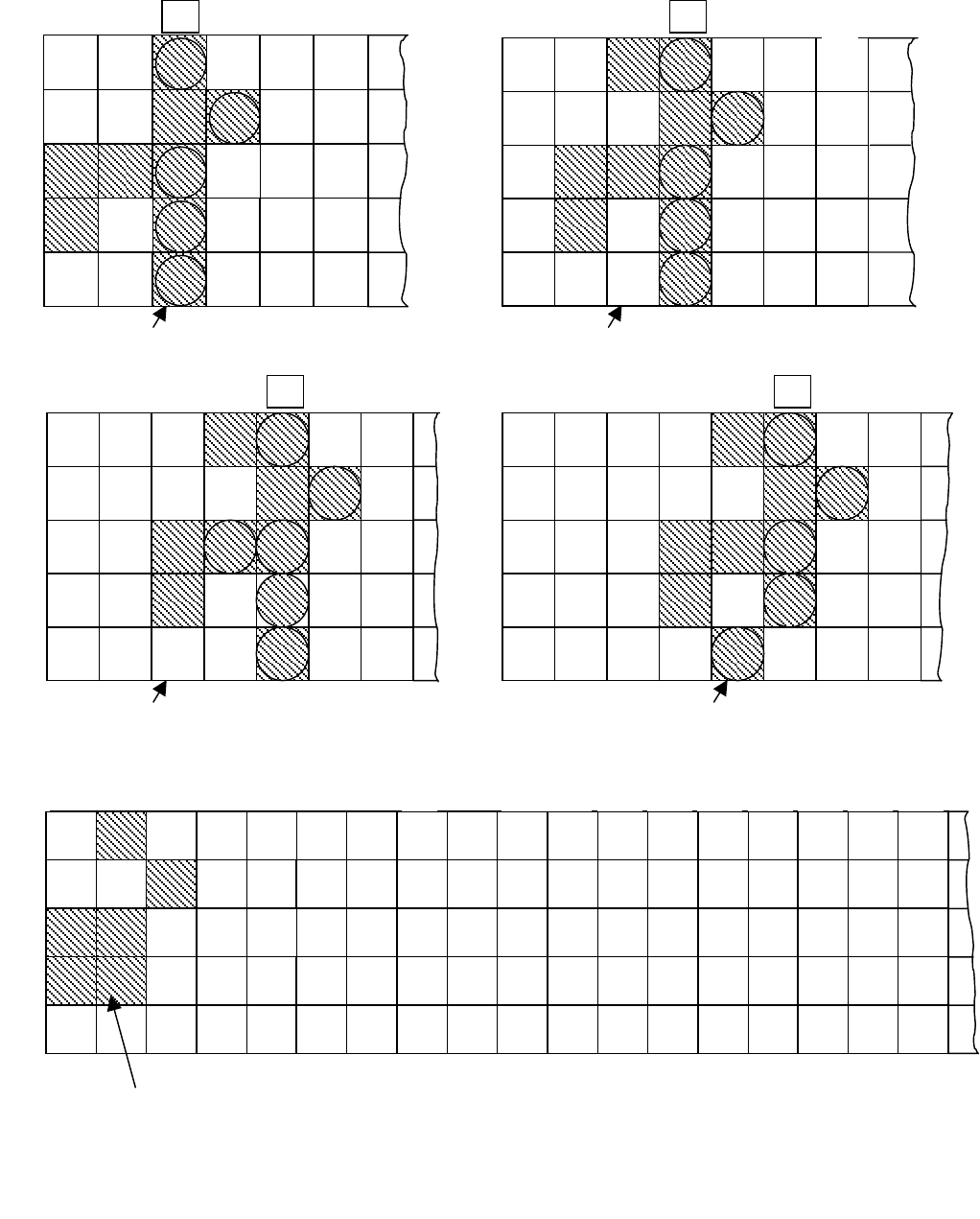
203

переменной

4

s - это 0, 1, 2, 3, так как уравнение для

4

s берется по модулю 4;

порождающая переменная

3

s имеет то же множество состояний, что и

4

s , так

как обе эти переменные определены через одну и ту же переменную пред-

ставляющей системы (то есть

243

VSS

=

). Первой осмысленной позицией

5

v

4

v

3

v

2

v

1

v

t = 1 2

3

4 5 …

а)

6

Сп

р

авочник

1

1 1

5

1

5

1

5

б)

5

v

4

v

3

v

2

v

1

v

t = 1 2 3

4

5 6

Сп

р

авочник

…

1 1

1 1 5

5

1

2

0

9

7

5

v

4

v

3

v

2

v

1

v

t = 1 2 3 4

5

в)

6

Сп

р

авочник

…

1 11

1 1 1

1 1 5

1 1 5 0

95

0

2

5

4

0

5

v

4

v

3

v

2

v

1

v

t = 1 2 3 4

5

6

г)

Сп

р

авочник

7

1 11 0

1 1 1 2

1 1 25 0

1 1 5 5 0

95

0

4

8 …

4

9

5

v

4

v

3

v

2

v

1

v

t

=

1

2

3

4

5

6

д)

Начальное условие

7

1 11 0 0 1 0

8

1 0 10 0 0 0 0 0

t

=

10

11

12

1

3

1

4

1

5

1

6

1

7

…

11 1 2 0 1 0 3 00 1 0 2 0 2

1 1 25 0 4 2 5 0 5 65 2 0 3 5 3

1 1 05 5 4 0 3 7 3 43 7 5 1 3 1

95 4 4 9 2 7 2 32 6 4 0 2 0

Рисунок В.3 - Данные, порожденные в порядке возрастания значений пара-

метра t (пример В.1)

204

маски на матрице данных ( позиция определяется положением справочника

маски) является позиция 3

=

t

; позиции 1

=

t

и 2

=

t

смысла не имеют, так как

состояния некоторых выборочных переменных для этих позиций не опреде-

лены (

ρ

+

t

не входит в множество

T

). Начальное условие состоит из шести

элементов матрицы данных:

2,1

v ,

3,2

v ,

1,3

v ,

1,4

v ,

2,4

v . Пусть, например, все эти

элементы равны 1. Ещё пять элементов матрицы данных -

1,1

v ,

1,2

v ,

2,2

v ,

1,5

v ,

2,5

v - не могут быть порождены, а могут быть заданы пользователем, но для

порождения данных эти переменные не нужны. На рисунке В.3а, б, в, г под-

робно показано порождение состояний соответственно для t = 3, 4, 5, 6;

кружками обведены порожденные состояния. На рисунке В.3д показано на-

чальное условие и несколько больший фрагмент порожденной матрицы дан-

ных.

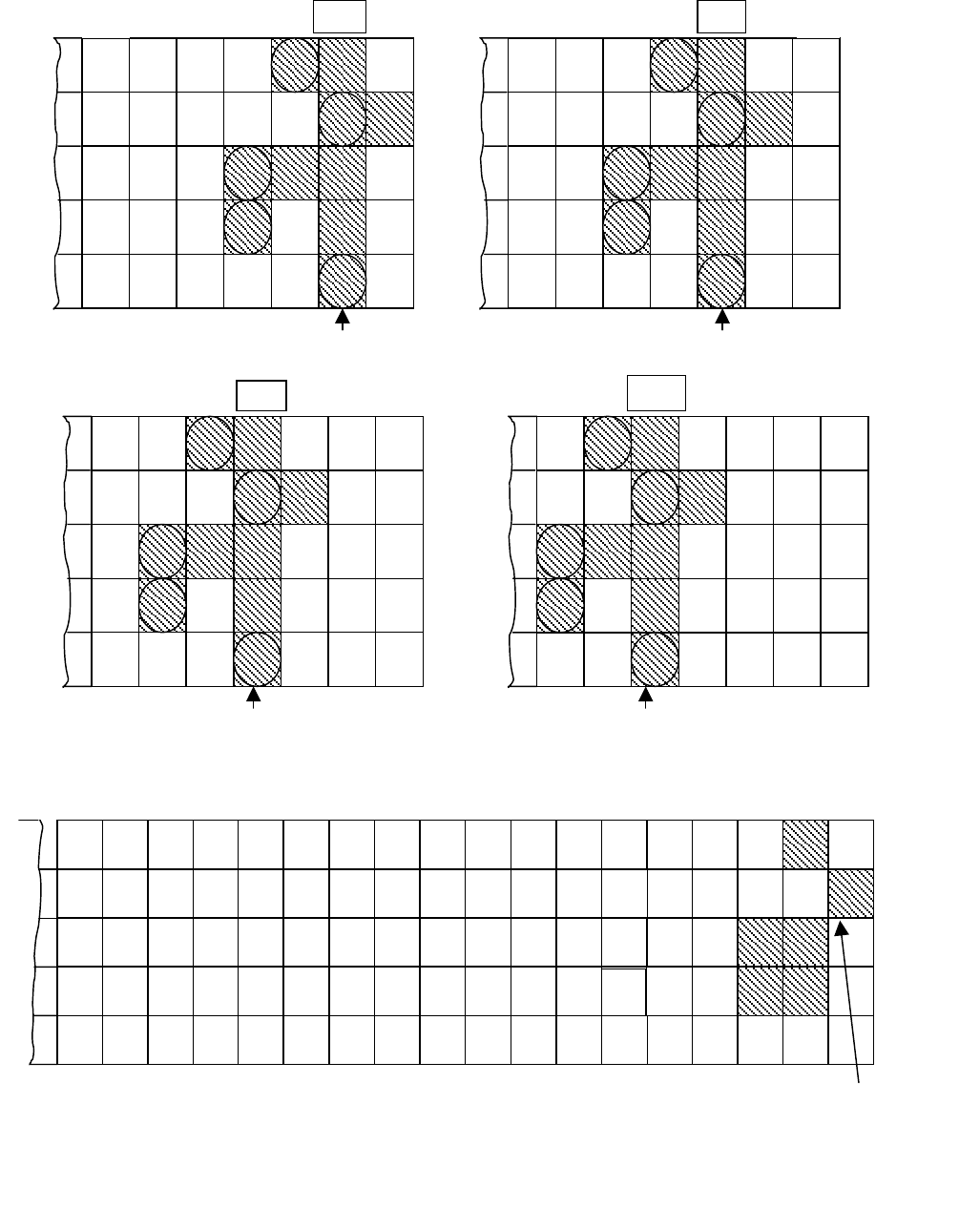
Если данные порождаются в порядке убывания t (смотри рисунок В.4),

то порождаемыми переменными являются переменные, представляющие ле-

вый край маски, то есть переменные

1

s ,

3

s ,

5

s ,

8

s ,

10

s . Данные в матрице

данных порождаются справа налево. Предположим теперь, что

GB

f опреде-

ляется уравнениями

ttttttk

ssssss

,9,7,6,4,2,

+

+= (mod k+1)

при k = 1, 3, 5, 8, 10. Порождение данных при t = 98, 97, 96, 95 подробно по-

казано на рисунке 3.4а, б, в и г. На рисунке В.4д показано начальное условие

и несколько больший фрагмент порожденной матрицы.

В.3 Методологические отличия

Хотя функция выбора является, вероятно, наиболее подходящим фор-

мальным аппаратом для задания ограничений в детерминированных систе-

мах, в которых порождение данных удобно описывать с помощью функции

(В.16), для работы с недетерминированными системами функции выбора не

годятся.

Традиционно с недетерминированными системами работают в теории

вероятностей. Несмотря на то, что это наиболее развитый и важнейший ма-

тематический инструмент, в настоящее время вероятностная мера рассматри-

вается только как частный случай более общего класса мер, называемого не-

четкими мерами.

В нашем случае меры определяются на подмножествах декартового

произведения С. Отсюда мера определяется функцией

µ: Р(С)→[0,1], (В.17)

где Р(С) – мощность множества С. Чтобы функция являлась мерой, она

должна обладать следующими свойствами нечетких мер:

205

() ()

()

0

).lim()1(lim

...,21...21)3(

);2()1(,212

;1)(;001

→

=

⊇⊇⊆⊆

≤⊆

=

i

XiX

то

ХХилиХХесли

ХХтоххесли

С

µ

µµµ

µ

Требование (µ1) очевидно. Требование (µ2), обычно называемое свойст-

91

t =99

9

97 96

9

999

t =

98888888

…

t =

4

v

2

v

4

v

2

v

t =

5

v

4

v

3

v

2

v

1

v

9

98

9995

а)

9

Сп

р

авоч-

1 1

1

1 1

1

5

…

5

9…

5

v

4

v

3

v

2

v

1

v

9

97

9994

б

)

Сп

р

авоч-

t =

1 1

1 5 1

1 15

5

1

3

0

5

9

9…

5

v

4

v

3

v

2

v

1

v

99

9

6

994

в

)

Сп

р

авоч-

1 1 1

11 1

1 5 1 3

1 1 0 5

5 9

1

3

6

4

9 9…

5

v

3

v

1

v

99994

г)

Сп

р

авоч-

t =

1 1 1 1

1 1 1 3

1 5 1 33

1 1 0 56

5 4 9

1

2

4

1

0

9

5

v

3

v

1

v

д)

Начальное

у

словие

1 1 1 1010101 11 1 1 00

1 1 3 1 2301011 10 3 2 31

1 5 1 3343035 25 2 3 55

1 5 1 0

6

16305 88 2 6 82

5 4 9 1419856 69 0 7 49

Рисунок В.4 - Данные, порожденные в порядке убывания значений пара-

метра t (пример В.1)

95

206

вом монотонности , не допускает, чтобы подмножество другого подмножест-

ва С обладало большей мерой, чем включающее подмножество. Согласно

требованию (µ3), называемому непрерывностью, предел мер бесконечной

монотонной последовательности. К дискретным системам, в которых С все-

гда является конечным множеством, требование непрерывности, естественно,

неприменимо.

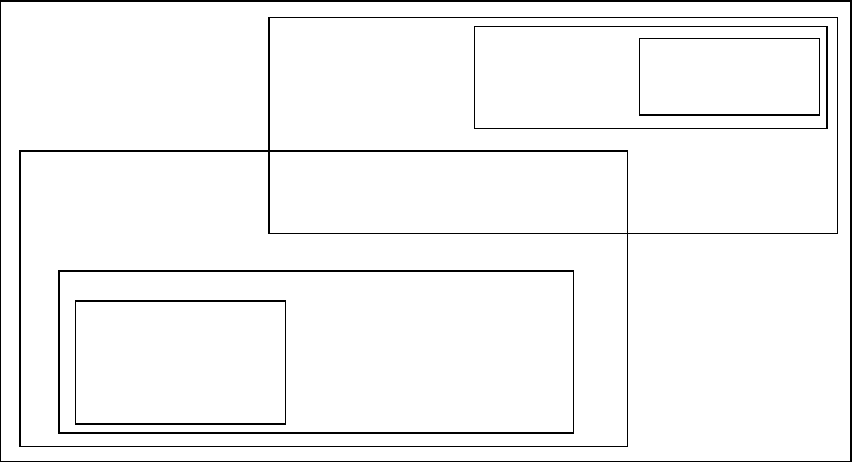
В литературе описаны самые разные классы нечетких мер, имеющих

разные свойства. На рисунке В.5 приведена диаграмма, изображающая от-

ношение включения для некоторых мер. Так, например, класс вероятностных

мер входит в класс мер правдоподобия и в класс мер доверия, но не пересе-

кается с классами мер возможности или необходимости.

Классы нечетких мер рассматриваются как методологические отличия.

Они используются в порождающих системах и во всех системах более высо-

ких эпистемологических уровней.

Далее будут рассматриваться только два класса мер. Первый - классиче-

ский и хорошо разработанный класс вероятностных мер, второй – это класс

возможностных мер. Необходимо отметить, что возможные меры приложи-

мы только к конечным множествам и к некоторым частным случаям беско-

нечных множеств; в общем случае эти меры не удовлетворяют требованию

непрерывности. Таким образом, они наверняка применимы к дискретным, но

не к непрерывным системам.

Из теории вероятностей хорошо известно, что любая вероятностная мера

p, однозначно определяется функцией распределения

[

]

1,0: →Cf

B

, (В.18)

Рисунок В.5 – Некоторые классы нечетких мер

которая должна удовлетворять соответствующим требованиям согласно

формуле

Нечеткие

меры

Меры

доверия

(убежденности)

Меры

необходимости

Вероятностные Меры прав-

меры доподобия

Возможно-

стные меры

Четкая воз-

можность

Четкая необ-

ходимость

(уверенность)

207

(

)

(

)

∑

∈

=

Xc

B

cfXp , (В.19)

где

()

CPX ∈ . Здесь применен тот же индекс B, что и в описании функ-

ции поведения, определенной в (В1), так как плотность вероятности также

будет использоваться в качестве функции поведения.

Мера возможностей – это функция

(

)

[

]

1,0: →CP

π

, (В.20)

удовлетворяющая следующим требованиям:

(π1)

() ( )

;1;00 == C

π

(π2)

()

ii

i

XX

π

max)( =∪

Хорошо известно, что мера возможности π однозначно определяется

функцией распределения возможностей f

B

, имеющей вид (В8) и определяе-

мой формулой

(

)

B

Xc

fX

∈

=

max

π

. (В.21)

В.4 От систем данных к системам с поведением

Важный класс системных задач, часто называемый индуктивным моде-

лированием систем, может быть описан в первом приближении как множест-

во задач, связанных с подъемом по эпистемологической иерархии систем.

Все задачи этого класса характеризуются следующим общим описанием: да-

но

Конкретная система, скажем x определенного эпистемологического

уровня;

Множество всех конкретных систем некоего более высокого эпистемо-

логического уровня, совместимых с системой x (то есть основанных на той

же представляющей системе, с теми же методологическими отличиями),

скажем множество Y;

Набор соответствующих требований Q относительно неких свойств сис-

тем из множества из множества Y, причем одним из этих требований являет-

ся требование, чтобы данная система x была аппроксимирована как можно

более точно системой более высокого уровня и требуется определить Y

Q

–

подмножество Y, такое, чтобы любая система из Y

Q

удовлетворяла всем тре-

бованиям, определенным в наборе Q.

Для демонстрации в данном разделе задачи определения систем с пове-

дением, представляющих заданную систему данных и обладающих некими

подходящими дополнительными свойствами, будем считать, что x – это сис-

тема данных с номинальными переменными (переменными с номинальной

шкалой), Y – множество всех систем с поведением с вероятностными или

возможностными функциями поведения, совместимыми с x, а набор Q состо-

ит из:

1) подмножества Y

r

– множества Y, определенного пользователем или

УРСЗ (как выбор по умолчанию);

208

2) требования, чтобы несогласованность между соответствующими пе-

ременными заданной системы данных и системы с поведением из Y

Q

была

как можно меньшей;

3) требования, чтобы степень неопределенности при порождении дан-

ных системой с поведением из множества Y

Q

была как можно меньшей;

4) требования, чтобы система из подмножества Y

Q

была как можно бо-

лее простой;

5) предпочтения требования 2 требованиям 3 и 4.

В этой общей формулировке требование 1 сводится к определению

множества допустимых масок. Если параметрическое множество не упорядо-

чено, то понятие параметрического соседства не определено, и, следователь-

но, существует только одна осмысленная маска. Эта маска, определяемая то-

ждественным правилом сдвига; она называется маской без памяти. Эта зада-

ча сводится к определению для имеющихся данных функции распределения

вероятностей или возможностей, удовлетворяющих требованию 2. Она реша-

ется полным перебором данных с помощью маски без памяти (в данном слу-

чае порядок выбора не важен) и определения для каждого состояния выбо-

рочных переменных

с ( в данном случае они совпадают с основными пере-

менными) числа N(

c) их появлений в данных. Числа N(c) для всех с∈С обыч-

но называются частотами состояний

с. Они используются для вычисления

по некоторым правилам соответствующих функций вероятностей или

возможностей.

Вычислять распределение вероятности или возможности по частотам

можно разными способами. Выбор способа зависит от того, какой смысл

придает пользователь этим вероятностям или возможностям. Так, например,

если вероятности рассматриваются как характеристики данных, то обычно

вычисляются относительные частоты, то есть отношения N(

с) к общему

числу имеющихся выборок из данных по используемой маске. Отсюда

()

(

)

()

∑

∈

=

C

B

N

cN

cf

α

. (В.31)

Если, однако, вероятности рассматриваются как оценки частот по уже

имеющимся результатам наблюдения, то они вычисляются по формуле

()

(

)

(

)

(

)

)||(1

∑

∈

+

=

C

B

CNcNcf

α

. (В.32)

Поскольку распределения возможностей менее ограничены, чем их ве-

роятностные аналоги (например, к ним не надо добавлять 1), существует еще

больше возможных правил для вычисления их по частотам N(

c). Естествен-

ный способ вычислений распределения возможностей, который можно счи-

тать аналогом формулы (42) – это считать значение возможности равной от-

ношению частоты N(

c) к максимальной зафиксированной частоте, то есть

(

)

(

)

(

)

α

NcNcf

C

B

∈

=

max . (В.33)

По другой формуле распределение возможности вычисляются по соот-

ветствующим вероятностям. Пусть

(

)

cf

B

и

(

)

cf

B

′

- это соответственно воз-

209

можность и вероятность состояния с

(

)

Cc

∈

.

Тогда

(

)

(

)

(

)

[

]

∑

∈

′

=

C

BBB

fcfcf

α

,min . (В.34)

По этой формуле распределение возможностей выражается через верх-

ние границы значений вероятностей.

Предположим теперь, что параметрическое множество полностью упо-

рядочено. В этом случае из одной и той же системы данных можно получить

множество систем с поведением, отличающихся масками. Если для заданных

данных они определены достаточно корректно, то они одинаково хорошо от-

вечают требованию согласованности. Точнее, выражение «достаточно кор-

ректно» означает, что функция поведения хорошо согласуется с данными (и,

возможно, с некоторой дополнительной информацией) с точки зрения маски

и типа выбранных ограничений.

Всякая маска представляет собой некоторое окно, через которое отби-

раются рассматриваемые данные из матрицы данных (или из массива более

высокого порядка). При движении этого окна вдоль всей матрицы данных

частоты состояний соответствующих выборочных переменных определяются

подсчетом того, как часто наблюдается каждое состояние.

Число столбцов в маске называют глубиной маски и обозначают ∆М.

Есть по крайней мере два соображения, по которым применение масок с

большой глубиной в общем случае не желательно. Во-первых, если маска ис-

пользуется для порождения данных, то чем больше ее глубина, тем большее

требуется начальное условие. Это, вообще говоря, не желательно. Во-вторых,

если маска используется для выборки данных, то число неполных выборок

равно 2(∆М-1). Это означает, что с ростом глубины маски все меньше имею-

щихся данных используется для определения функции поведения. Следова-

тельно, с увеличением глубины маски сужается эмпирическая основа, на ко-

торой строится функция поведения.

Как выяснено выше, любая система определяется таким образом, что

она хорошо согласуется с заданной системой данных и дополнительной ин-

формацией по маске и принятому типу описания ограничений. Таким обра-

зом, требование согласованности имеет более высокий приоритет, чем ос-

тальные требования. Теперь остается только применить условия 3) и 4)

обычно называемые условием детерминированности и условием простоты,

для вывода подмножества решений Y

Q

ограниченного множества Y

r

.

Несмотря на то, что в формулировках конкретных типов задач возника-

ют и дополнительные требования, условия детерминированности и простоты

имеют всеобщее значение. Поэтому обычно они не опускаются. Часто снача-

ла определяется множество решений, удовлетворяющих этим условиям (и,

разумеется, условию согласованности), а затем входящие в это множество

системы с поведением изучаются исследователем. Он может использовать их

в качестве вспомогательного представления базовых переменных. Однако,

если необходимо дальнейшее сокращение множества решений, исследова-

тельпроизводит их оценку и сравнение согласно некоторым вспомогатель-

210

ным критериям. Эти критерии могут определяться как контекстом, так и вку-

сами исследователя.

В.5 Меры нечеткости

Степень недетерминированности должна измеряться обобщенной нечет-

костью, сопутствующей порождению данных. А значит, она должна быть оп-

ределена через порождающие функции поведения

GB

f и

GB

f

€

для нейтраль-

ных и направленных систем с поведением. Если эти функции представляют

собой функции распределения вероятностей, то мера обобщенной нечеткости

хорошо известна – это шенноновская энтропия, введенная К. Шенноном в

1948 году.

Обозначим через Р множество всех распределений вероятностей, кото-

рые могут быть определены на конечных множествах альтернативных (вза-

имно исключающих) исходов. Тогда вероятностная мера нечеткости – это

функция

[

]

∞

→ ,0: PH ,

обладающая некоторыми свойствами. Следующие свойства являются необ-

ходимыми свойствами любой содержательной меры нечеткости:

Н1 симметричность – нечеткость инвариантна относительно переста-

новки вероятностей;

Н2 расширяемость – нечеткость не меняется при добавлении к рассмат-

риваемому множеству исходов с нулевой вероятностью;

Н3 квазиаддитивность – нечеткость совместного распределения веро-

ятностей не больше суммы нечеткостей соответствующих безуслов-

ных распределений его компонентов;

Н4 аддитивность – для распределений вероятностей любых двух неза-

висимых множеств исходов нечеткость совместного распределения

вероятностей равна сумме нечеткостей отдельных распределений ве-

роятностей;

Н5 непрерывность – нечеткость – это непрерывная функция на всех

своих аргументах.

Известно, что только функции вида

(

)()

(

)

(

)

∑

∈

−

=

∈

Xx

b

xfxfaXxxfH log|

обладают свойствами Н1-Н5;

(

)

PXxxf

∈

)|(

- это распределение вероятностей для определенного конечного множества X

альтернативных исходов x, где a – произвольная положительная константа, а

b- произвольное основание логарифмов. Если потребовать выполнения еще и

нормализующего свойства

(

)

15.0;5.0

=

H

(нечеткость двух равновероятных исходов равна 1), то мера нечеткости опре-

деляется однозначно:

Миронов С.В., Пищухин А.М. Метасистемный подход в управлении

Подождите немного. Документ загружается.