Миронов С.В., Пищухин А.М. Метасистемный подход в управлении

Подождите немного. Документ загружается.

351

смотреть вопрос об использовании такого формализма. Однако применение

этого подхода встречает некоторые трудности.

Прежде всего следует неким конструктивным образом определить, что по-

нимается под «существенным различием функций поведения». То есть для прида-

ния понятию «разница» конкретного смысла необходимо выбрать функцию рас-

стояния для функций поведения. Кроме того, нужно задаться каким-то порого-

вым значением расстояния для определения того, что это расстояние «сущест-

венно». Несмотря на то, что принятие этих решений предоставляется пользовате-

лю, УРСЗ должен располагать неким вариантом решений, которые использу-

ются по умолчанию (при наличии соответствующего запроса).

Во-вторых, разница (расстояние) между локальной и глобальной функ-

циями поведения может считаться существенной только в том случае, когда

локальная функция определена на достаточно большом подмножестве парамет-

рического множества. И снова должно быть принято решение, какой наимень-

ший размер подмножества параметрического множества может считаться дос-

таточным, чтобы на нем можно было бы определить содержательную локальную

функцию поведения. Размер этот зависит от числа состояний переменных, от ме-

ры, с помощью которой задаются ограничения на переменные, от используемой

маски и, возможно, от каких-то других факторов.

Помимо отмеченных теоретических проблем, в задаче определения сущест-

венных локальных ограничений имеются и трудности практического характера.

Они связаны прежде всего с тем, что число подмножеств параметрического

множества, рассматриваемых в процессе определения существенных программ-

ных ограничений, с ростом параметрического множества растет экспоненци-

ально. Как следствие с ростом параметрического множества лавинообразно рас-

тет число необходимых вычислений, так что эта задача становится неразреши-

мой даже для параметрических множеств относительно небольшого размера.

В заключение этого раздела опишем простую процедуру определения ло-

кальных ограничений. Будем называть ее процедурой идентификации метаси-

стемы. Эта процедура использует предположение о том, что параметрическое

множество Т полностью упорядочено и что переменные описываются системой

данных. Эта процедура или не определяет никакой метасистемы (если не на-

ходится существенных локальных ограничений), или определяет метасистему,

состоящую из последовательности определенных на параметрическом множестве

систем с поведением. Замена одной системы на другую происходит при опреде-

ленных значениях параметра, которые вычисляются этой процедурой.

Даны: система данных с полностью упорядоченным параметрическим мно-

жеством T = N

, маска (обычно наибольшая допустимая) и определенный

способ представления ограничений на переменные (со своей мерой порождаю-

щей нечеткости). Процесс идентификации метасистемы состоит в следующем.

Шаг 1. Пусть дано целое число m, рациональное число ∆ и известно, что

t=1, k=1.

Шаг 2. Необходимо определить функцию поведения для подмножества

данных, соответствующих отрезку [t, t+m] параметрического множества, и

вычислить ее порождающую нечеткость U

352

Шаг 3. Затем надо увеличить k на 1; если t+km∉T, то перейти на

шаг 6.

Шаг 4. Определить функцию поведения для подмножества данных, соот-

ветствующего отрезку [t, t+km] параметрического множества, и вычислить ее

порождающую нечеткость U

Шаг Д. Если | U

- U

k-1

/max (U

, U

k-1

)<∆, то перейти на шаг 3; иначе за-

писать t+(k—l ) m в качестве аппроксимированной точки замены элементов

метасистемы, t=(k—l)m, k присвоить значение 1 и перейти на шаг 2.

Шаг 6. Стоп.

В основе этой процедуры лежит следующее наблюдение: если данные не

имеют существенных локальных ограничений, то порождающие нечеткости ло-

кальных функций поведения для отрезков [1, t] с ростом t быстро сходятся

(после некоторых начальных возмущений) к значениям, лежащим в малом

интервале ∆; напротив, если данные содержат существенное локальное огра-

ничение, например, на отрезке параметрического множества [t

, t

], то порождаю-

щие нечеткости обычно демонстрируют значительно превосходящие ∆ колеба-

ния около значений параметра t

и t

, а внутри отрезка [t

, t

] снова находятся

внутри небольшого интервала. Таким образом, существенные вариации поро-

ждающей нечеткости после того, как она колебалась в небольшом интервале,

позволяют считать данную систему метасистемой, каждый элемент которой соот-

ветствует некоему подмножеству параметрического множества.

Чувствительность и вычислительная сложность данной процедуры суще-

ственным образом зависят от выбранных значений m и ∆. Для оказания помо-

щи пользователю в выборе этих значений УРСЗ должен располагать соответст-

вующими характеристиками, полученными в результате вычислительных экспе-

риментов, подобных тем, что описаны в главе 4 для анализа реконструируе-

мости. Можно также выполнить эту процедуру несколько раз при разных значе-

ниях m, ∆ и усреднить полученные результаты. Как бы то ни было, эта процедура

определяет возможные точки замены только приблизительно. Для более точного

определения и оценки их существенности необходимо провести более общее

исследование.

Пример Д.8. В данном примере описывается применение процедуры иден-

тификации метасистемы при оценке работы пилотов в процессе их трениров-

ки на летных тренажерах. Исходная система состоит из четырех переменных,

Таблица Д.2 - Описание системы, рассматриваемой в примере Д.8

Каналы наблюдения

Характеристика: Скорость Высота над Курс Расстояние

уровнем моря

Переменная: s a r d

Единицы: Узлы Футы Градусы Мор. мили

относительно

магнитного

353

севера

1 [150, 170) [1700—1840)

[0—93)

[0-2,6)

2 [170, 220] [1840—2400]

[93—113]

[2,6-14)

3 [220, 250) [2400—2700) [113—122) [14—21)

4 [250—270) [2700—4900) [122—360) >21

5 ≥270 [4900—6900) — —

6 — [6900—22800) — —

Интерпретация

состояний

7 — >22800 — —

Матрица данных

s 444455555555555555555555555555555555555555555554444444333

а 777666666666666666666666666666666666666666666666666655555

r 211111111111111111111111111111111111111111111111111111222

d 444444444444444444444444444444444444433333333333333333333

s 333333333333332222222222222111111111111111111111111111111

а 555555555555444444444444444444333333333333333333333333333

r 222333333333333333333333333333333333333333333333333333333

d 333333333333333322222222222222222222222222222222222222222

s 1111111111111112222233333333333333333333333333333

а 3222222111111112222223334444444444444444444444444

r 3333333333333333333344444444444444444444444444444

d 2222222222111111111111111111222222222222222222222

описывающих соответствующие характеристики реактивного самолета; па-

раметром является время. Не вдаваясь в технические подробности, будем ка-

ждую переменную описывать ее идентификатором, соответствующей харак-

теристикой и множеством состояний:

s — скорость, множество состояний N

;

а — высота, множество состояний N

;

r — курс, множество состояний N

;

d — расстояние, множество состояний N

Каналы наблюдения и матрица данных для этих переменных приведены

в таблице Д.2. Матрица, в которой данные представлены в порядке воз-

растания времени, описывает типичный (идеальный, правильный) способ

захода на посадку реактивного самолета. Весь период захода на посадку

разделен на 163 равных временных интервала, и для каждого определены

соответствующие состояния переменных. Матрица данных, приведенная в

таблице 8.2, является своего рода эталоном, по которому оценивается рабо-

та тренирующихся летчиков. И для курсантов, и для инструкторов желатель-

но, чтобы вся задача была естественным образом разбита на подзадачи

так, чтобы было легче локализовать ошибки.

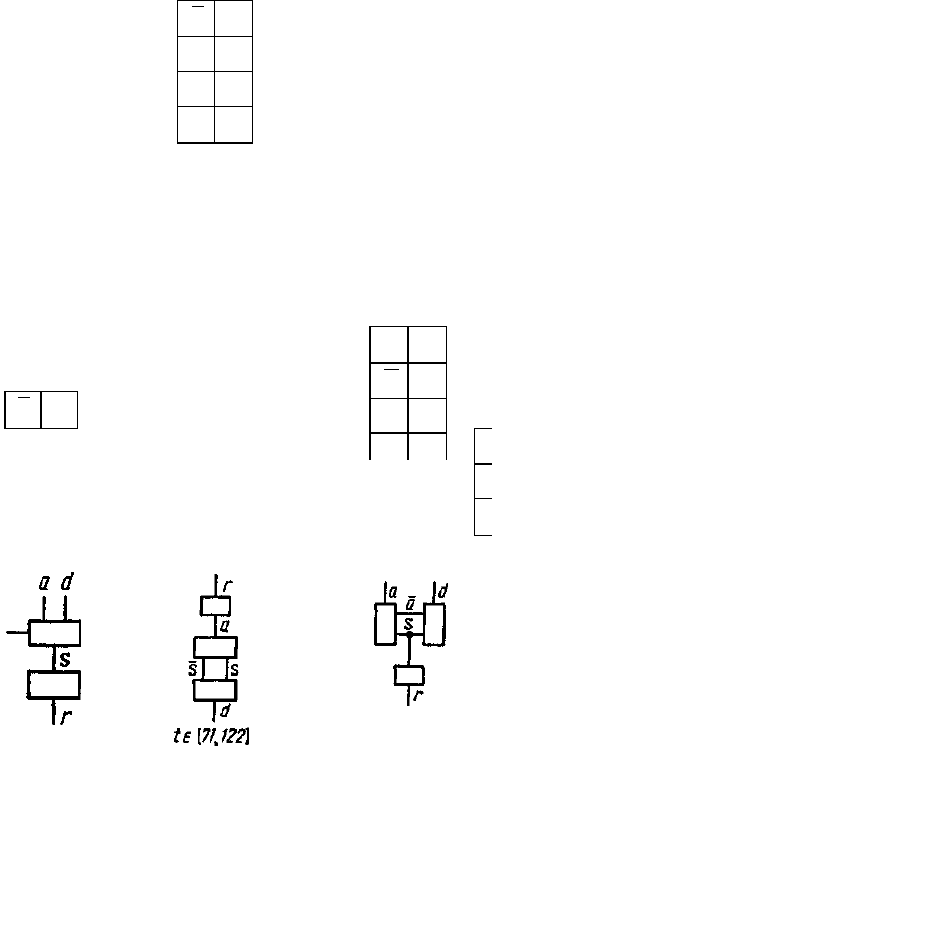
354

Процедура модификации метасистемы была

применена к матрице данных, приведенной в таблице Д.2 для

вероятностной функции поведения, маски из двух

столбцов и ∆=0.1. Процедура выполнена для нескольких значений

т.

Полученные для разных значений т точки замены были

затем ус- реднены. В результате получена метасистема,

состоящая из трех элементов, определенных соответственно на следующих

отрезках времени: 1—70, 71—122, 123—163. На самом деле, три этих эле-

мента являются естественными этапами выполнения посадки. Они соответст-

вуют снижению высоты, полету по дуге с заходом на

посадочный курс и собствен- но посадке.

Рисунок Д.8 - Метасистема для

типичного захода на посадку реак-

тивного самолета (пример Д.8)

[

701∈

[

163123

∈

SFSFSF

123

→

Для каждого элемента ме-

тасистемы была проведена

оценка маски (раздел 3.6) и вы-

полнена процедура реконструк-

ции (раздел Д.7). Полученные

езультаты приведены на рисун-

ке Д.8. Это система типа MSF

Понятно, что по сравнению с

обобщенной системой с поведе-

нием данная система позволяет

более точно оценивать работу

курсантов.